г. Оренбург октябрь 2016 года
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Площадь параллелограмма
Содержание
- 1. Презентация по математике Площадь параллелограмма
- 2. Тема урока:Площадь параллелограмма
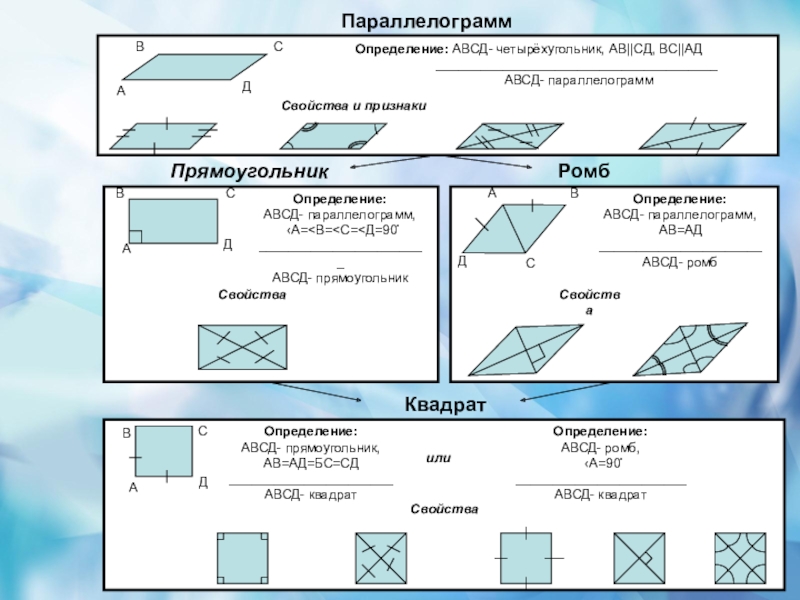
- 3. КвадратПараллелограммПрямоугольникРомбАВСДОпределение: АВСД- четырёхугольник, АВ||CД,
- 4. 1. Равные многоугольники имеют равные площади .
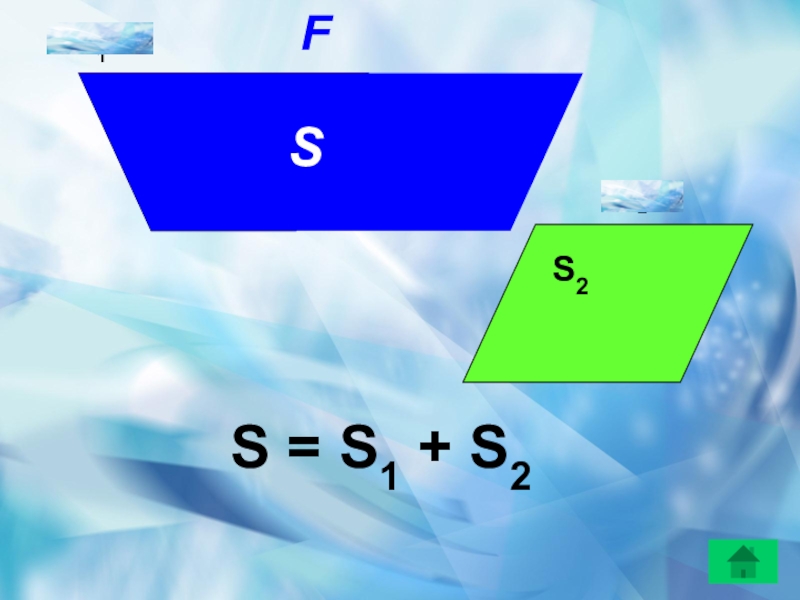
- 5. F1F2S1S2 SFS = S1 + S2
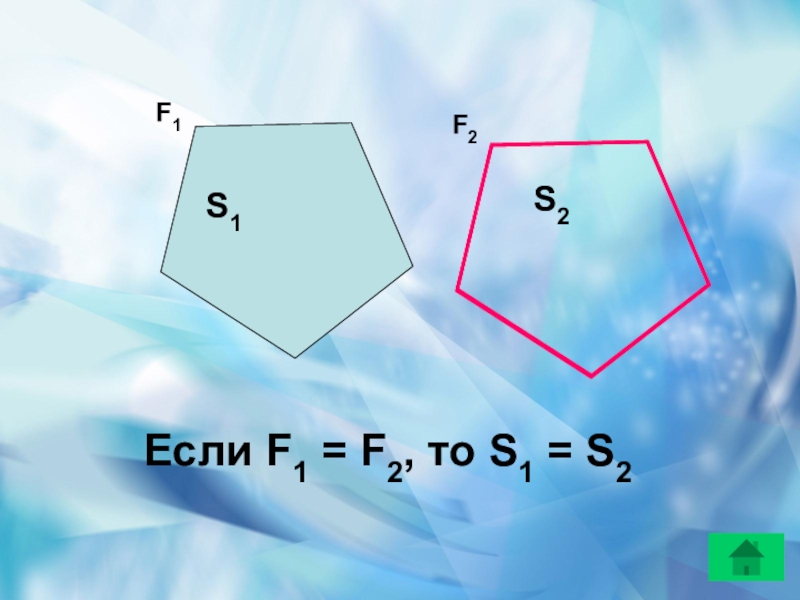
- 6. F2S1S2F1Если F1 = F2, то S1 = S2
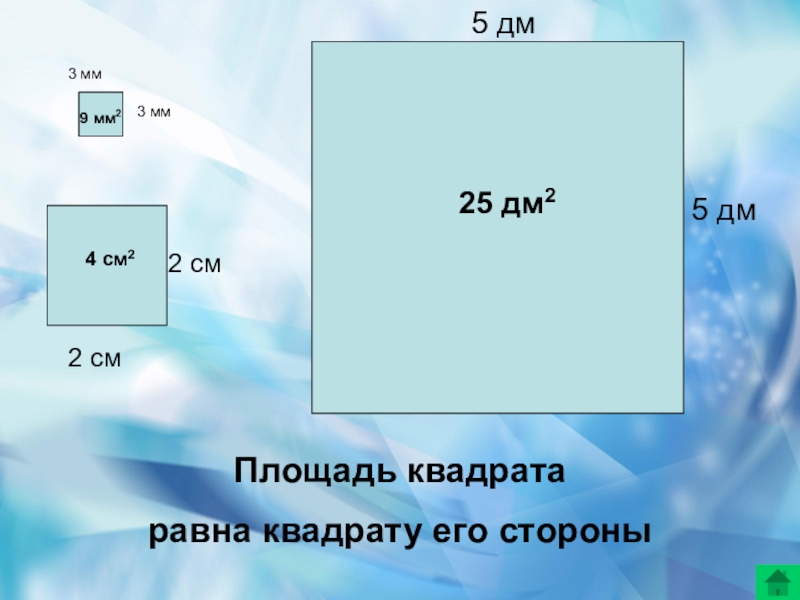
- 7. 3 мм3 мм2 см2 см5 дм5 дмПлощадь квадрата равна квадрату его стороны9 мм24 см225 дм2
- 8. Равновеликие фигуры 1. «Перекроите» прямоугольник в
- 9. АВС«Перекраивание» треугольника в трапециюМNK
- 10. Перекраивание прямоугольника в параллелограмм .
- 11. Слайд 11
- 12. Прямоугольник и параллерограмм - равновеликие фигуры.
- 13. Прямоугольник и параллерограмм - равновеликие фигуры.Перекраивание параллелограмма в прямоугольник .
- 14. Слайд 14
- 15. Парралерограмм и прямоугольник – равновеликие фигуры.
- 16. KABCDHВопрос: как найти площадь параллелограмма?АВ = CD
- 17. Как же найти площадь параллелограмма?ABCDHКSАВСD = AD · BHSАВСD = CD · BK
- 18. Вывод формулы площади параллелограмма.Теорема:Площадь параллелограмма равна произведению
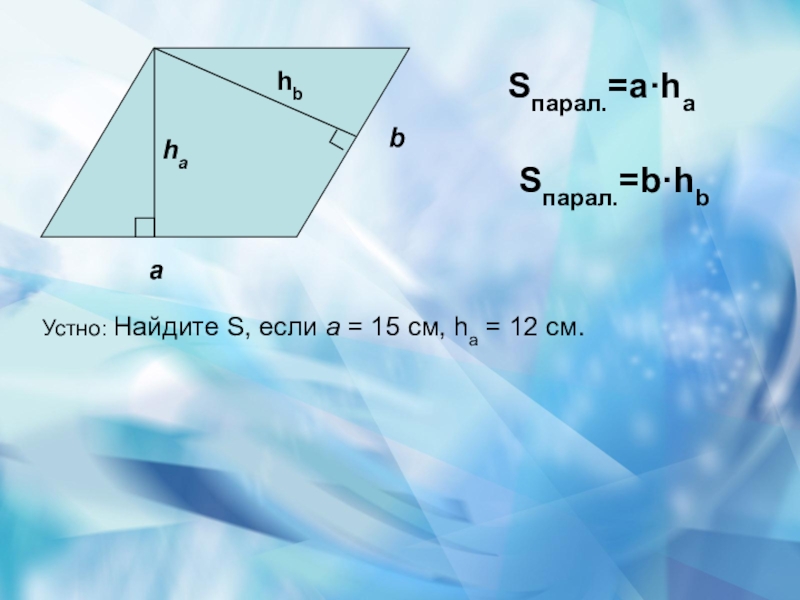
- 19. Sпарал.=а·haSпарал.=b·hbУстно: Найдите S, если а = 15 см, ha = 12 см.bhb
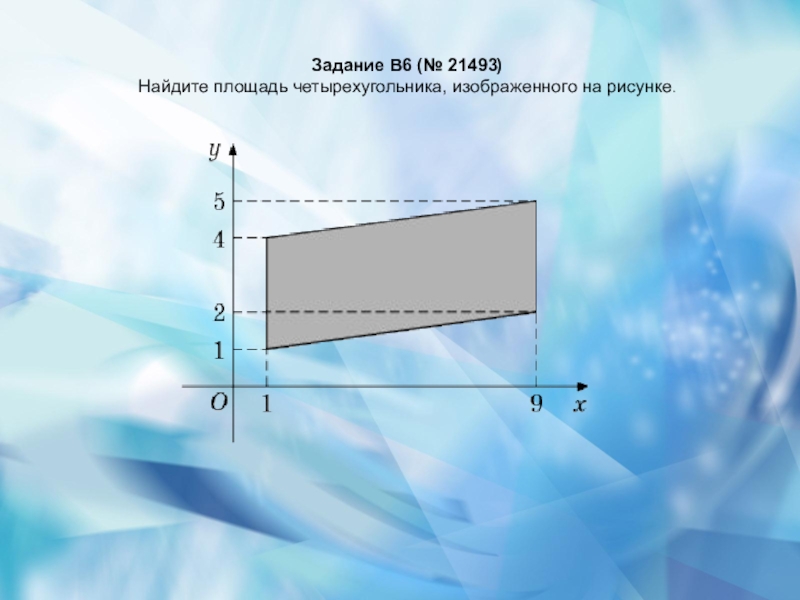
- 20. Задание B6 (№ 21493)Найдите площадь четырехугольника, изображенного на рисунке.
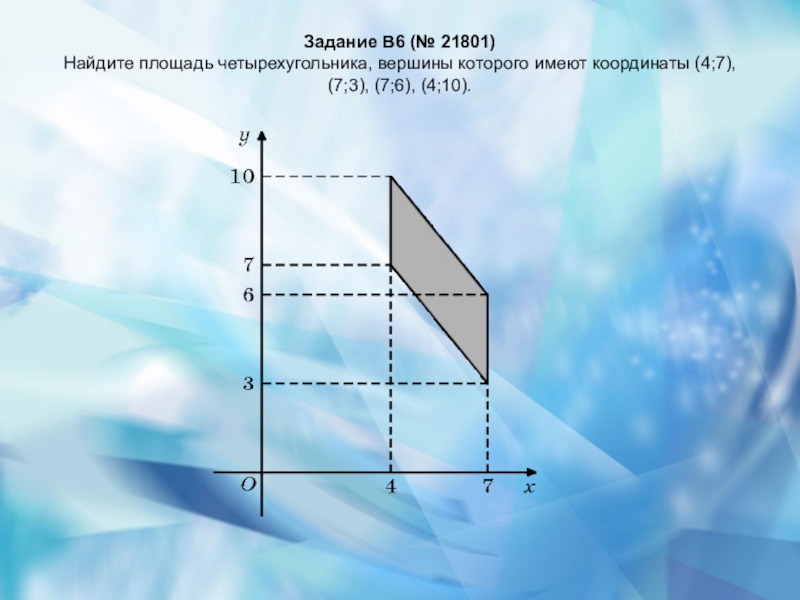
- 21. Задание B6 (№ 21801) Найдите площадь четырехугольника,
- 22. кино - так записывается по-гречески название
- 23. Древний грек сказал бы об этом четырёхугольнике: «Это же обыкновенный тетрагон». О каком четырёхугольнике идёт речь?
- 24. Разгадав ребус, вы узнаете, как называли со
- 25. Дельтоид Дельтоид — четырехугольник, обладающий двумя парами сторон одинаковой
- 26. Домашнее задание.Составить 2 ребуса ,Зашифровав в них
- 27. Тест 2. Угадай вид четырёхугольника ABCD, построй
- 28. 1 вариант Стороны параллелограмма
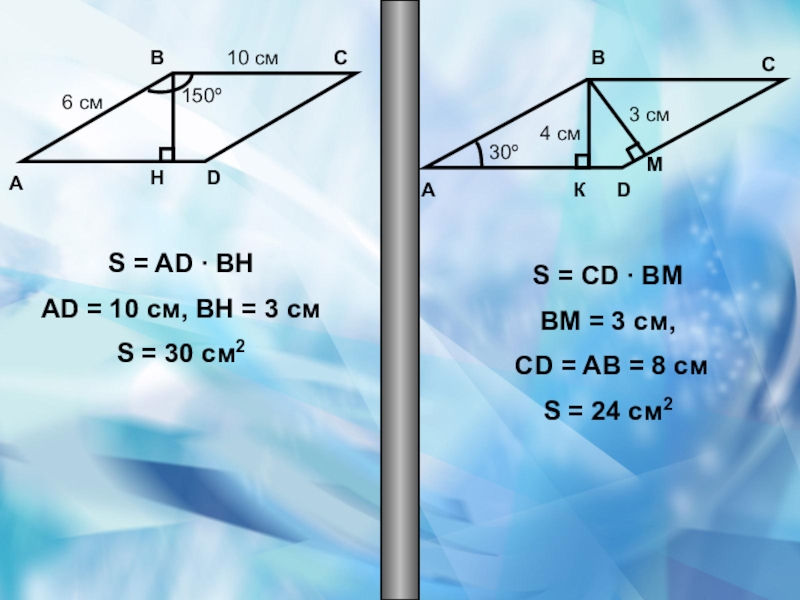
- 29. АВСD150º10 cм6 cмВСD30º3 cм4 cмАКМНS = AD
- 30. Итоги урока1. Достигли мы поставленной цели?2. Какой
- 31. Всем спасибо.
Тема урока:Площадь параллелограмма
Слайд 1Урок геометрии
в 8 классе по теме
«Площадь параллелограмма»
Разработан
учителем математики МБОУ « Лицей №6» имени З.Г. Серазетдиновой Кузнецовой С.Д.
Слайд 3 Квадрат
Параллелограмм
Прямоугольник
Ромб
А
В
С
Д
Определение: АВСД- четырёхугольник, АВ||CД, ВС||АД
______________________________________
АВСД- параллелограмм
АВСД- параллелограмм
Определение: Свойства и признаки А В С Д Свойства Определение: А В С Д Свойства Определение: или Определение: Свойства А В С Д
АВСД- параллелограмм,
‹А=
АВСД- прямоугольник
АВСД- параллелограмм,
АВ=АД
______________________
АВСД- ромб
АВСД- прямоугольник,
АВ=АД=БС=СД
______________________
АВСД- квадрат
АВСД- ромб,
‹А=90ْ
_______________________
АВСД- квадрат
Слайд 41. Равные многоугольники имеют равные площади .
2. Если
многоугольник составлен из нескольких многоугольников , то его площадь равна сумме площадей этих многоугольников .
Свойства площадей
Слайд 8
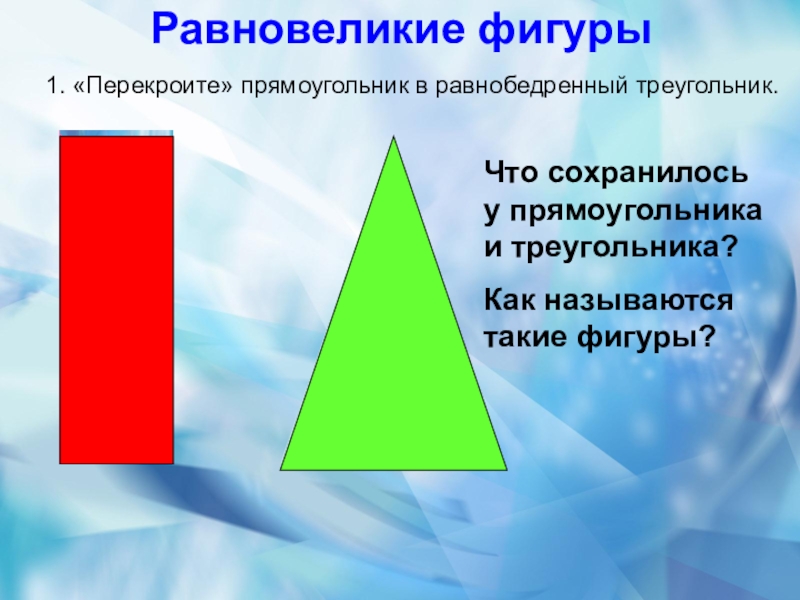
Равновеликие фигуры
1. «Перекроите» прямоугольник в равнобедренный треугольник.
Что сохранилось у прямоугольника и
треугольника?
Как называются такие фигуры?
Как называются такие фигуры?
Слайд 13Прямоугольник и параллерограмм - равновеликие фигуры.
Перекраивание параллелограмма в прямоугольник .
Слайд 16K
A
B
C
D
H
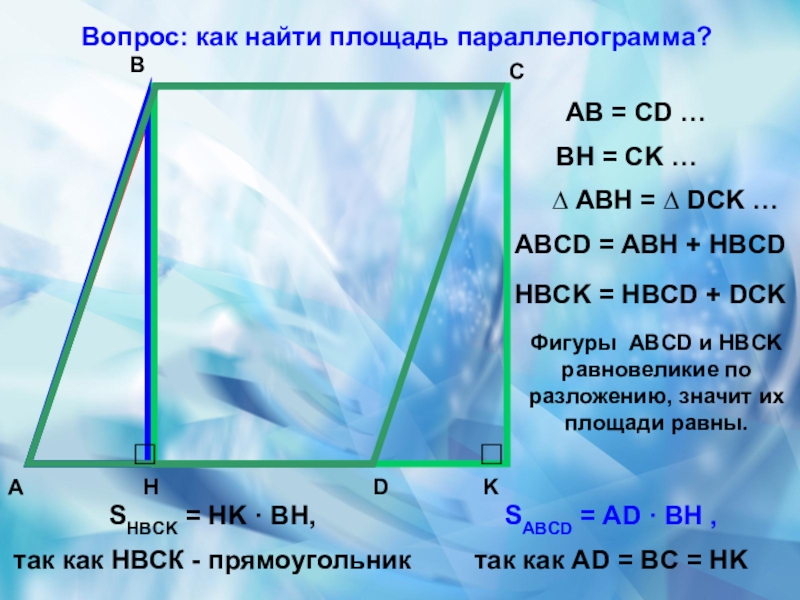
Вопрос: как найти площадь параллелограмма?
АВ = CD …
BH = CK …
∆ ABH = ∆ DCK …
ABCD = ABH + HBCD
HBCK = HBCD + DCK
Фигуры ABCD и HBCK равновеликие по разложению, значит их площади равны.
SABCD = AD · BH ,
так как AD = BC = HK
SHBCK = HK · BH,
так как НВСК - прямоугольник
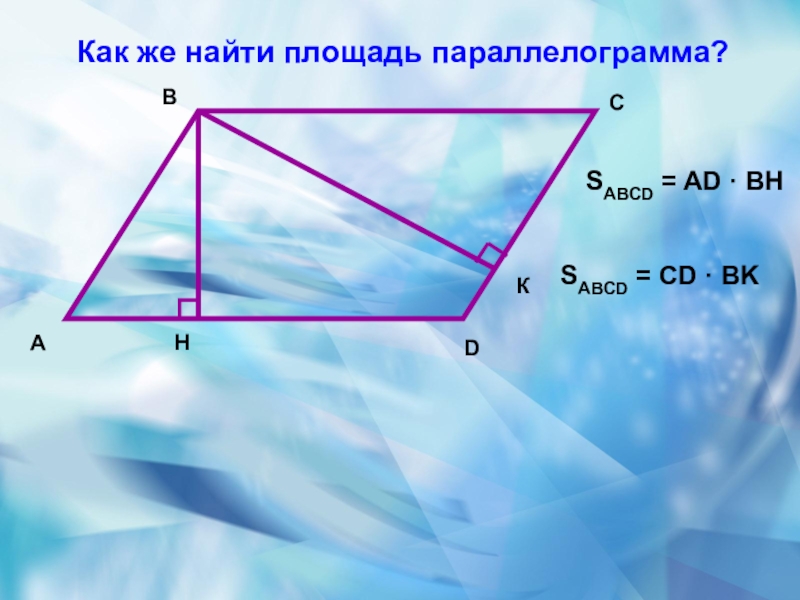
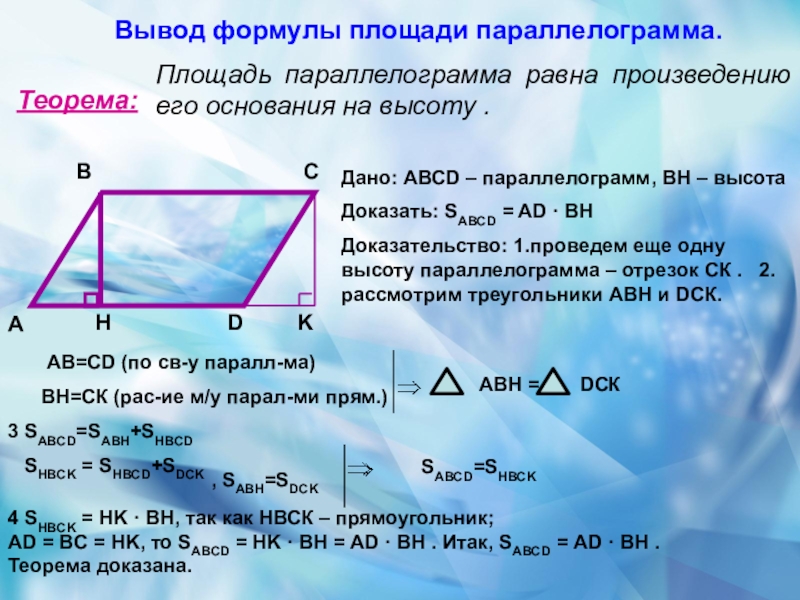
Слайд 18Вывод формулы площади параллелограмма.
Теорема:
Площадь параллелограмма равна произведению его основания на высоту
.
A
B
C
D
H
Дано: АВСD – параллелограмм, ВН – высота
Доказать: SABCD = AD · BH
Доказательство: 1.проведем еще одну высоту параллелограмма – отрезок СК . 2.рассмотрим треугольники АВН и DСК.
K
АВ=СD (по св-у паралл-ма)
ВН=СК (рас-ие м/у парал-ми прям.)
3 SABCD=SABH+SHBCD
SHBCK = SHBCD+SDCK
, SABH=SDCK
SABCD=SHBCK
4 SHBCK = HK · BH, так как НВСК – прямоугольник;
AD = BC = HK, то SABCD = HK · BH = AD · BH . Итак, SABCD = AD · BH .
Теорема доказана.
АВН =
DСК
Слайд 21Задание B6 (№ 21801) Найдите площадь четырехугольника, вершины которого имеют координаты (4;7),
(7;3), (7;6), (4;10).
Слайд 22кино
- так записывается по-гречески название этого четырёхугольника. Расшифровав ребус,
вы узнаете, как его записываем мы.
Слайд 23Древний грек сказал бы об этом четырёхугольнике: «Это же обыкновенный тетрагон».
О каком четырёхугольнике идёт речь?
Слайд 24Разгадав ребус, вы узнаете, как называли со времён Евклида до XVII
века любой четырёхугольник, отличный от параллелограмма.
Слайд 25Дельтоид
Дельтоид — четырехугольник, обладающий двумя парами сторон одинаковой длины. В отличие от параллелограмма,
равными являются не противоположные, а две пары смежных сторон. Дельтоид имеет форму, похожую на воздушного змея.
Слайд 26Домашнее задание.
Составить 2 ребуса ,
Зашифровав в них следующие четырехугольники : Параллелограмм
и дельтоид.
Решить задачи № 459 (в,г).
№ 460 , 464 (б) .
Решить задачи № 459 (в,г).
№ 460 , 464 (б) .
Слайд 27Тест 2. Угадай вид четырёхугольника ABCD, построй его и вычисли его площадь,
приняв одну клетку за 1 см.
Если у четырёхугольника ABCD
AB ll CD, AB = CD то этот четырёхугольник – …
Если у параллелограмма ABCD
AC = BD,
то этот четырёхугольник – …
Если у прямоугольника ABCD
AC BD, то этот четырёхугольник – …
Слайд 281 вариант
Стороны
параллелограмма
равны 10 см
и 6 см, а
угол между ними 150º.
Найдите
площадь этого
параллелограмма.
угол между ними 150º.
Найдите
площадь этого
параллелограмма.
2 вариант
Острый угол параллелограмма равен 30º, а высоты, проведенные из вершины тупого угла равны 4 см и 3 см.
Найдите
площадь этого параллелограмма.
Слайд 29А
В
С
D
150º
10 cм
6 cм
В
С
D
30º
3 cм
4 cм
А
К
М
Н
S = AD ∙ BH
AD = 10
cм, ВН = 3 см
S = 30 cм2
S = 30 cм2
S = CD ∙ BM
BM = 3 cм,
CD = AB = 8 cм
S = 24 cм2
Слайд 30Итоги урока
1. Достигли мы поставленной цели?
2. Какой главный итог нашего урока?
3.
Что мы использовали для достижения цели урока?
