- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Пирамида
Содержание
- 1. Презентация по математике Пирамида
- 2. Цель урока: Изучить новый вид многогранников – пирамидаВыйти на понятие правильной пирамиды, усечённой пирамидыИзучить свойства пирамиды
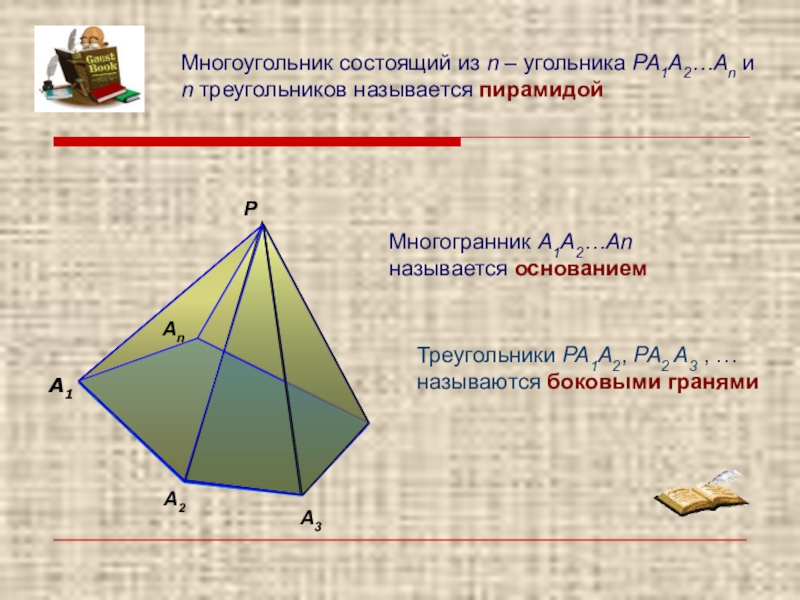
- 3. А2А3РМногоугольник состоящий из n
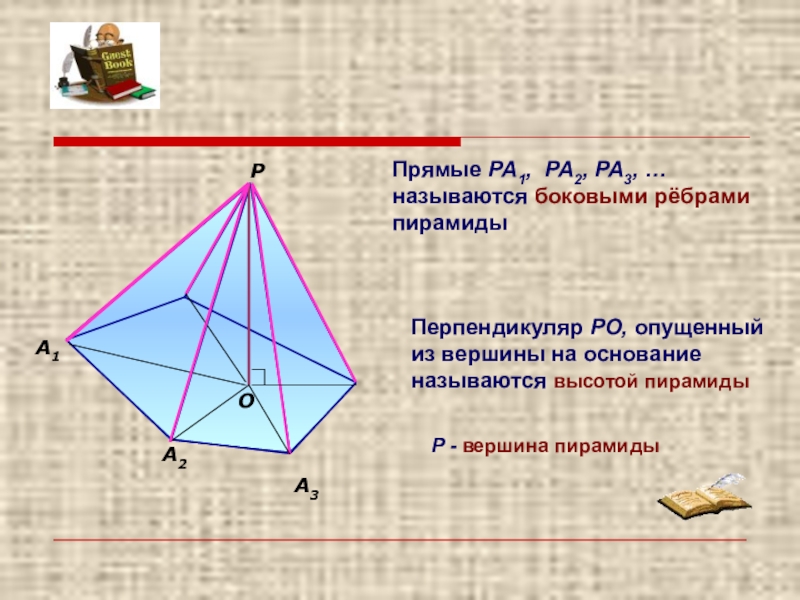
- 4. А1РА2А3Прямые РА1, РА2, РА3, … называются боковыми
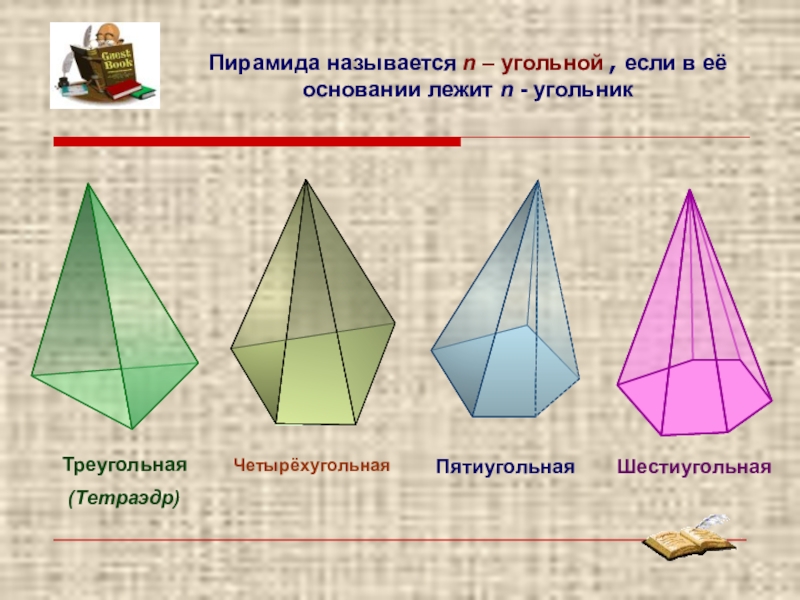
- 5. Пирамида называется n – угольной , если в её основании лежит n - угольник
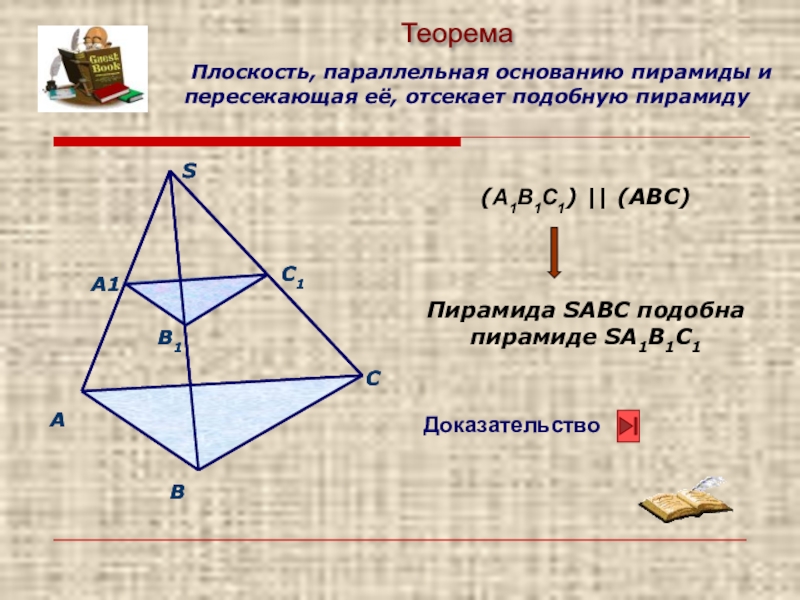
- 6. (А1В1С1) || (АВС)Пирамида SАВС подобна пирамиде SА1В1С1
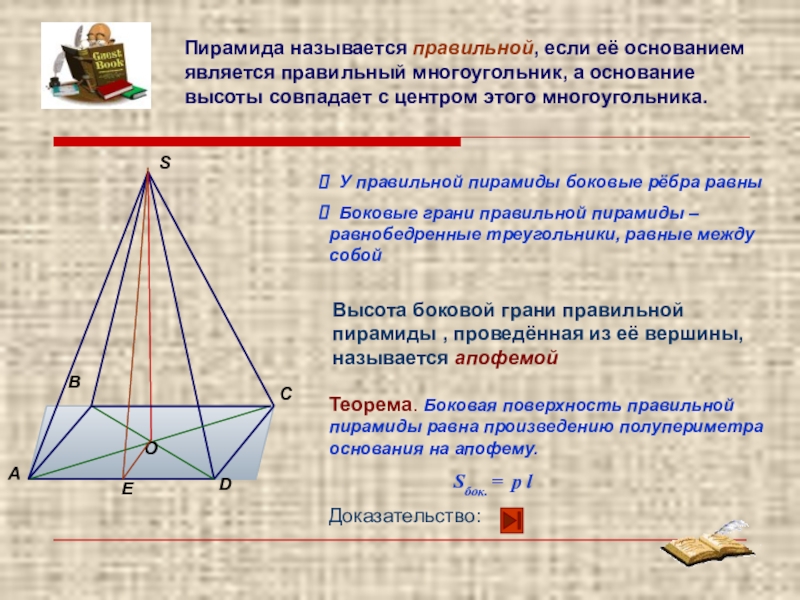
- 7. Пирамида называется правильной, если её основанием является
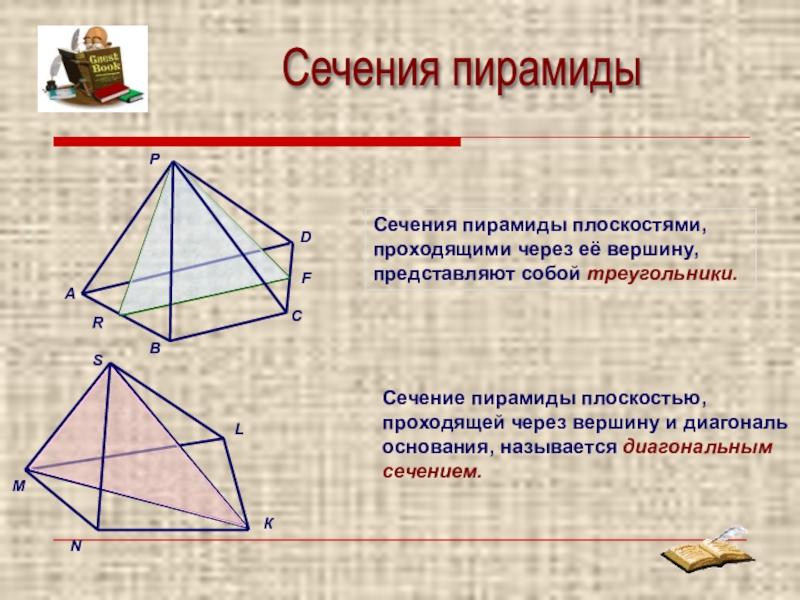
- 8. Сечение пирамиды плоскостью, проходящей через вершину и
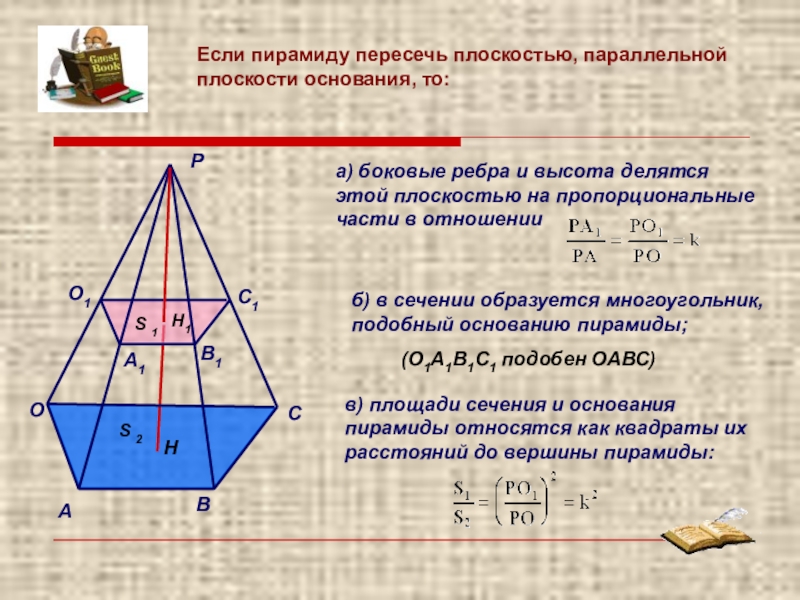
- 9. Если пирамиду пересечь плоскостью, параллельной плоскости основания,
- 10. Грани усечённой пирамиды, лежащие в параллельных
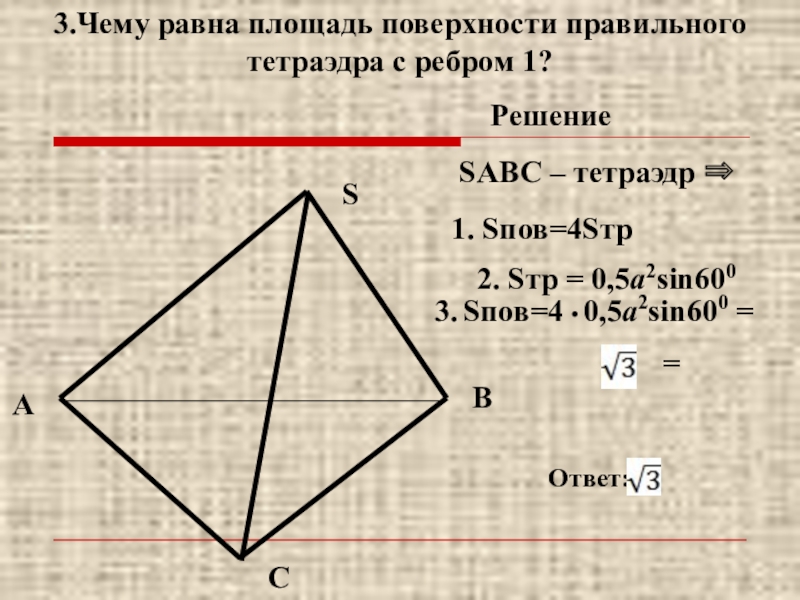
- 11. ABCSSABC – тетраэдр ⇒ 3.Чему равна площадь
- 12. 4. Найдите площадь боковой поверхности пирамиды Хеопса,
- 13. 3. Постройте сечение пирамиды, плоскостью, проходящей через
- 14. Домашнее задание1). Если в правильной треугольной пирамиде
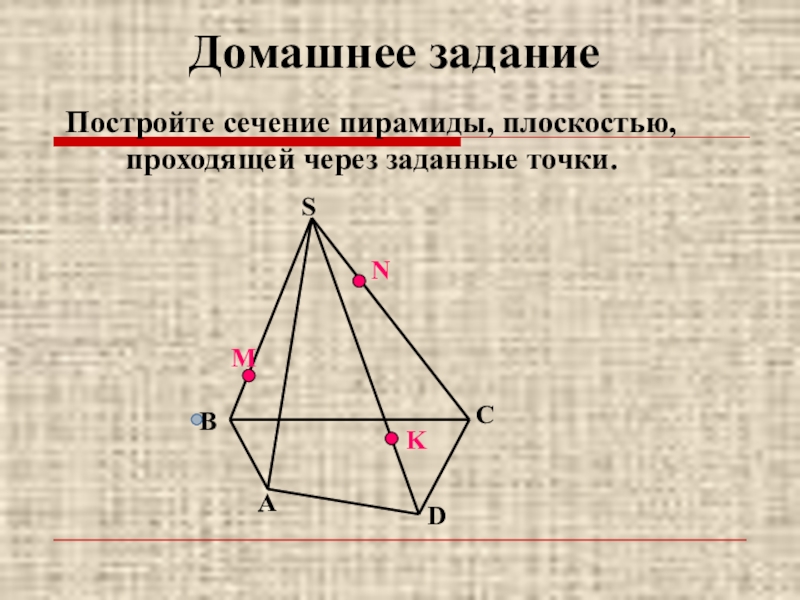
- 15. Постройте сечение пирамиды, плоскостью, проходящей через заданные точки.МNKABCDSДомашнее задание
Слайд 2Цель урока:
Изучить новый вид многогранников – пирамида
Выйти на понятие правильной
Изучить свойства пирамиды
Слайд 3
А2
А3
Р
Многоугольник состоящий из n – угольника РА1А2…Аn и
Многогранник А1А2…Аn называется основанием
Треугольники РА1А2, РА2 А3 , … называются боковыми гранями
Аn
А1
Слайд 4А1
Р
А2
А3
Прямые РА1, РА2, РА3, … называются боковыми рёбрами пирамиды
О
Перпендикуляр РО, опущенный
Р - вершина пирамиды
Слайд 7
Пирамида называется правильной, если её основанием является правильный многоугольник, а основание
У правильной пирамиды боковые рёбра равны
Боковые грани правильной пирамиды – равнобедренные треугольники, равные между собой
Высота боковой грани правильной пирамиды , проведённая из её вершины, называется апофемой
Теорема. Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему.
Sбок. = р l
Доказательство:
Слайд 8Сечение пирамиды плоскостью, проходящей через вершину и диагональ основания, называется диагональным
Сечения пирамиды плоскостями, проходящими через её вершину, представляют собой треугольники.
Сечения пирамиды
Слайд 9Если пирамиду пересечь плоскостью, параллельной плоскости основания, то:
б) в сечении
(О1А1В1С1 подобен ОАВС)
Слайд 10 Грани усечённой пирамиды, лежащие в параллельных плоскостях называются основаниями пирамиды
Высота усеченной пирамиды - это общий перпендикуляр к плоскостям ее оснований (или его длина).
Усечённая пирамида, полученная из правильной пирамиды – правильная
Боковые грани правильной усечённой пирамиды – равные равнобокие трапеции, а их высоты называются апофемами
О
А
С
В
О1
С1
А1
В1
Теорема. Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров основания на апофему
S бок = (Р1 + Р2 ) · l
Доказательство:
Слайд 11A
B
C
S
SABC – тетраэдр ⇒
3.Чему равна площадь поверхности правильного тетраэдра с
Решение
1. Sпов=4Sтр
2. Sтр = 0,5а2sin600
Ответ:
3. Sпов=4 • 0,5а2sin600 =
=
Слайд 124. Найдите площадь боковой поверхности пирамиды Хеопса, сторона основания которой равна
О
E
S
D
С
В
А
Решение:
2. AC ∩ ВD = О
3. Пирамида правильная ⇒
SО ⊥ (АВС)
4. ОЕ ⎜⎜ СD ⇒ ОЕ ⊥ АD ⇒
5. SЕ ⊥ АD (по теореме о 3 перпендикулярах)
6. Δ SОЕ – п\у
по т. Пифагора
ЕS2 = ЕО2+ОS2 = 1152 + 1382 =
= 13225 +19044 = 32269
ЕS ≈ 180
7. ES - высота ΔАSD
SАSD = 0,5 ЕS•АD = 0,5 •180 • 230 =20700 м2
Ответ: 82800 м2
1. Sб.пов=4Sтр
8. Sб.пов=4Sтр = 4 • 20700 = 82800 м2
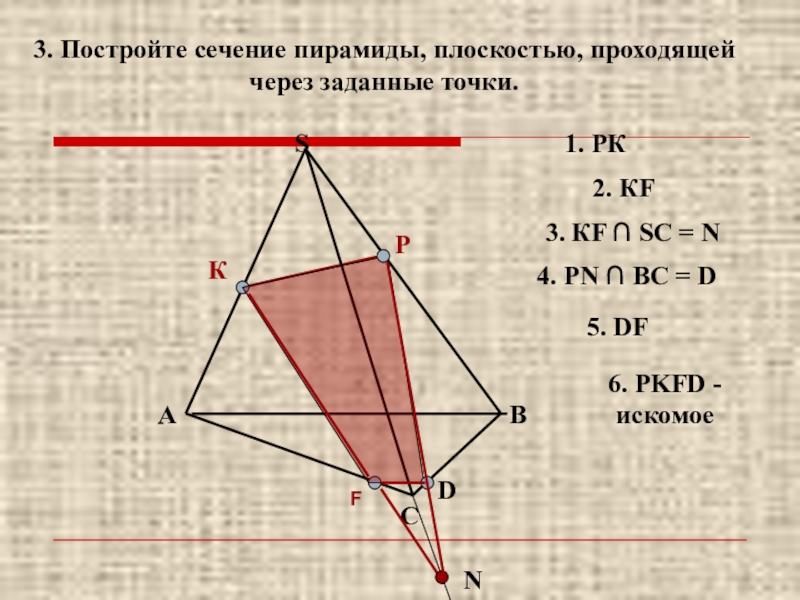
Слайд 133. Постройте сечение пирамиды, плоскостью, проходящей через заданные точки.
В
А
С
S
К
Р
F
1. РК
2. КF
3.
N
4. РN ∩ ВС = D
D
5. DF
6. PKFD - искомое
Слайд 14Домашнее задание
1). Если в правильной треугольной пирамиде высота H равна стороне
2). Сторона квадрата равна 10 см. Доказать, что нельзя, используя его в качестве основания, построить правильную четырехугольную пирамиду с боковым ребром 7 см.
3). Доказать или опровергнуть утверждение: «если в пирамиде все ребра равны, то пирамида правильная».