- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике: Пифагор и его теорема
Содержание
- 1. Презентация по математике: Пифагор и его теорема
- 2. ПланПредлагаем погрузится в проект "Теорема Пифагора" и
- 3. Пифагор - кто он?Пифагор Самосский (ок. 580
- 4. Пифагору приписывают ряд важных в то время
- 5. Пифагор жил в шестом веке до нашей
- 6. Он первый дал название своему роду деятельности.
- 7. История возникновения теоремыСегодня теорема Пифагора обнаружена в
- 8. Шутливая формулировкаЕсли дан нам треугольник И притом
- 9. Стихотворение о теореме А. фон Шамиссо
- 10. Доказательство МёльманнаПлощадь данного прямоугольного треугольника, с одной
- 11. Древнекитайское доказательствоМатематические трактаты Древнего Китая дошли до
- 12. Ключ к этому
- 13. Доказательство АннарицияБагдадский математик и астроном Х в.
- 14. Доказательство Евклида Дано: ABC-прямоугольный треугольник Доказать:SABDE=SACFG+SBCHIПусть ABDE-квадрат,
- 15. Очевидно, что углы CAE=GAB(=A+90°); отсюда следует, что
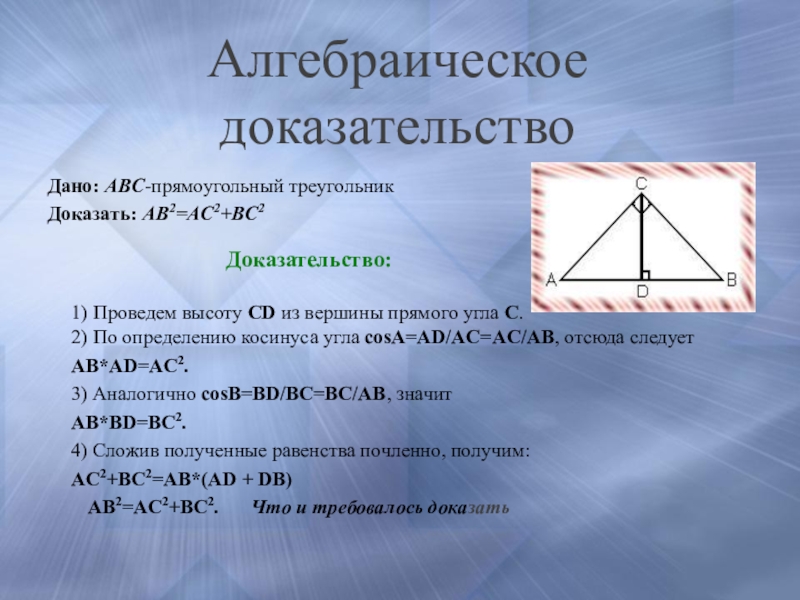
- 16. Алгебраическое доказательствоДано: ABC-прямоугольный треугольникДоказать: AB2=AC2+BC2 Доказательство: 1) Проведем высоту
- 17. Геометрическое доказательство Дано: ABC-прямоугольный треугольникДоказать: BC2=AB2+AC2Доказательство:1) Построим отрезок
- 18. Теорема Пифагора в
- 19. Слайд 19
- 20. В Греции была выпущена почтовая марка по
- 21. Литература1. Л.С. Атанасян, В.Т. Бутузов, С.Б. Кадомцев
- 22. Историческая справка Неизвестно, каким способом доказывал свою
- 23. Популярность теоремы Пифагора столь велика, что её
- 24. Известно более 100 доказательств теоремы.Последний штрих к
- 25. Задача древней Индии Над озером тихимС полфута
- 26. Легенда о смерти ПифагораСонную тишину ночного Метапонта
Слайд 2План
Предлагаем погрузится в проект "Теорема Пифагора" и ответить на главный вопрос
Пифагор – кто он?
История возникновения Теоремы Пифагора.
Какие способы доказательства теоремы Пифагора существуют?
Теорема Пифагора в искусстве.
Слайд 3Пифагор - кто он?
Пифагор Самосский (ок. 580 - ок. 500 до
Слайд 4Пифагору приписывают ряд важных в то время открытий, а именно: теорему
арифметикой. Пифагор много занимался пропорциями
и прогрессиями и, вероятно подобием фигур, так как ему
приписывают решение задачи: "По данным двум фигурам
построить третью, равновеликую одной из данных и подобную
второй". Пифагор и его ученики ввели понятие о многоугольных,
дружественных, совершенных числах и изучали их свойства.
Арифметика как практика вычислений не интересовала Пифагора,
и он с гордостью заявил, что "поставил арифметику выше
интересов торговца".Пифагор одним из первых считал, что Земля
имеет форму шара и является центром Вселенной, что Солнце,
Луна и планеты имеют собственное движение, отличное от
суточного движения неподвижных звезд.
Слайд 5Пифагор жил в шестом веке до нашей эры, имел красивую внешность,
Он первый дал название своему роду деятельности. Слово "философ", как и слово "космос" достались нам от Пифагора. В его философии много космического. Он утверждал, что для понимания Бога, человека и природы надо изучать алгебру с геометрией, музыку и астрономию. Кстати, именно пифагорейская система знаний, и называется по-гречески "математикой". Что касается пресловутого треугольника с его гипотенузой и катетами, то это, согласно великому греку, больше, чем геометрическая фигура. Это "ключ" ко всем зашифрованным явлениям нашей жизни. Всё в природе, говорил Пифагор, разделено на три части. Поэтому прежде чем решать любую проблему, её надо представить в виде треугольной диаграммы. "Узрите треугольник - и задача на две трети решена".
Слайд 6Он первый дал название своему роду деятельности. Слово "философ", как и
Слайд 7История возникновения теоремы
Сегодня теорема Пифагора обнаружена в различных
частных задачах и
треугольнике в папирусе времен фараона Аменемхета
Первого (ок. 2000 до н.э.), и в вавилонских
клинописных табличках эпохи царя Хаммурапи
(XVIII в. до н.э.), и в древнеиндийском
геометрическо-теологическом трактате VII —V вв. до н.э.
«Сульва сутра» («Правила веревки»). В древнейшем китайском трактате
«Чжоу-би суань цзинь», время создания которого точно не известно, утверждается, что в XII в. до н. э. китайцы знали свойства египетского треугольника, а к VI в. до н.э.—и общий вид теоремы. Несмотря на все это, имя Пифагора столь прочно сплавилось с теоремой Пифагора, что сейчас просто невозможно представить, что это словосочетание распадется. То же относится и к легенде о заклании быков Пифагором. Да и вряд ли нужно препарировать историко-математическим скальпелем красивые древние предания. Сегодня принято считать, что Пифагор дал первое доказательство носящей его имя теоремы. Увы, от этого доказательства также не сохранилось никаких следов.
Слайд 8Шутливая формулировка
Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы
Слайд 9Стихотворение о теореме
А. фон Шамиссо :
Уделом истины не может
Слайд 10Доказательство Мёльманна
Площадь данного прямоугольного треугольника, с одной стороны, равна 0,5*а*b ,
Слайд 11Древнекитайское доказательство
Математические трактаты Древнего Китая дошли до нас в редакции II
Слайд 12 Ключ к этому доказательству подобрать нетрудно. В самом
Если квадрат со стороной с вырезать и оставшиеся 4 затушеванных треугольника уложить в два прямоугольника, то ясно, что образовавшаяся пустота, с одной стороны, равна с², а с другой — а²+Ь², т.е. с²= а²+Ь².
Слайд 13Доказательство Аннариция
Багдадский математик и астроном Х в. ан-Найризий (латинилизированное имя –
Со времен Пифагора появилось несколько сотен доказательств его знаменитой теоремы, так что она попала в книгу рекордов Гиннеса.
Слайд 14Доказательство Евклида
Дано:
ABC-прямоугольный треугольник
Доказать:
SABDE=SACFG+SBCHI
Пусть ABDE-квадрат, построенный на гипотенузе
прямоугольного
ABC, а ACFG и BCHI-квадраты, построенные
на его катетах. Опустим из вершины C прямого
угла перпендикуляр CP на гипотенузу и продолжим
его до пересечения со стороной DE квадрата
ABDE в точке Q; соединим точки C и E, B и G.
Слайд 15Очевидно, что углы CAE=GAB(=A+90°); отсюда следует, что треугольники ACE и AGB(закрашенные
SPQEA=2SACE
Точно так же квадрат FCAG и треугольник BAG имеют общее основание GA и высоту AC; значит, SFCAG=2SGAB
Отсюда и из равенства треугольников ACE и GBA вытекает равновеликость прямоугольника QPBD и квадрата CFGA; аналогично доказывается и равновеликость прямоугольника QPAE и квадрата CHIB. А отсюда, следует, что квадрат ABDE равновелик сумме квадратов ACFG и BCHI, т.е. теорема Пифагора.
Слайд 16Алгебраическое доказательство
Дано: ABC-прямоугольный треугольник
Доказать: AB2=AC2+BC2
Доказательство:
1) Проведем высоту CD из вершины прямого угла
AB*AD=AC2.
3) Аналогично соsВ=BD/BC=BC/AB, значит
AB*BD=BC2.
4) Сложив полученные равенства почленно, получим:
AC2+BC2=АВ*(AD + DB)
AB2=AC2+BC2. Что и требовалось доказать
Слайд 17Геометрическое доказательство
Дано: ABC-прямоугольный треугольник
Доказать: BC2=AB2+AC2
Доказательство:
1) Построим отрезок CD равный отрезку AB
SABED=2*AB*AC/2+BC2/2
3) Фигура ABED является трапецией, значит, её площадь равна:
SABED= (DE+AB)*AD/2.
4) Если приравнять левые части найденных выражений, то получим:
AB*AC+BC2/2=(DE+AB)(CD+AC)/2
AB*AC+BC2/2= (AC+AB)2/2
AB*AC+BC2/2= AC2/2+AB2/2+AB*AC
BC2=AB2+AC2.
Это доказательство было опубликовано в 1882 году Гэрфилдом.
Слайд 18 Теорема Пифагора в
Теоремой Пифагора и пифагорейской школой восхищается человечество на протяжении всей истории, им посвящают стихи, песни, рисунки, картины. Так, художник Ф. А. Бронников (1827-1902) нарисовал картину « Гимн пифагорейцев восходящему солнцу»
Картина передаёт пафос преклонения учеников легендарной школы перед единой гармонией, царящей в мироздании, музыке и числе.
Слайд 20В Греции была выпущена почтовая марка по случаю переименования острова Самос
На марке надпись: «Теорема Пифагора. Эллас. 350 драхм».
Эта красивая марка - почти единственная среди многих тысяч существующих, на которой изображен математический факт.
Слайд 21Литература
1. Л.С. Атанасян, В.Т. Бутузов, С.Б. Кадомцев Геометрия 7-9 классы.
2. А.Г.
3. Энциклопедия для детей. Глав. ред. М.Д. Аксенова.
4. Электронная энциклопедия: Star World
5. Глейзер Г.И. История математики в школе.
6.Зенкевич И.Г. 15 свиданий с математикой.
7.Еленьский Щ. По следам Пифагора. М., 1961
8. Свешников А. Путешествия в историю математики. – М., 1995
9. Теорема Пифагора. – М., Знание – сила, №5,6 2000
Слайд 22Историческая справка
Неизвестно, каким способом доказывал свою теорему Пифагор. Несомненно лишь то,
Слайд 23Популярность теоремы Пифагора столь велика, что её доказательства встречаются даже в
Слайд 24Известно более 100 доказательств теоремы.
Последний штрих к портрету учёного. Он был
Слайд 25Задача древней Индии
Над озером тихим
С полфута размером
Высился лотоса цвет.
Он рос
И ветер порывом
Отнёс его в сторону. Нет
Боле цветка над водой.
Нашёл же рыбак его
Ранней весною
В двух футах от места, где рос.
И так, предложу я вопрос:
« Как озера вода здесь глубока?»
Слайд 26Легенда о смерти Пифагора
Сонную тишину ночного Метапонта прорезал острый крик .
Когда ночной караул прибыл на место проешествия, в колеблющемся свете факелов все увидели распростёртого на земле старца, и неподалёку от него – мальчика лет 12 с лицом, перекошенным от ужаса.
- Кто это ? – спросил начальник караула у мальчика. - Это Пифагор, - ответил тот.
- Кто такой Пифагор ? Среди жителей города нет гражданина с таким именем.
- Мы недавно прибыли из Кротона. Мой господин должен был скрываться от врагов, и выходил только ночью. Они выследили его и убили.
- Сколько их было?
- Я этого не успел заметить в темноте. Они отбросили меня в сторону и накинулись на него .
Начальник караула стал на колени и приложил ухо к к груди старца.
- Конец, - сказал начальник