- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Параллелепипед, призма, пирамида (9 класс)
Содержание
- 1. Презентация по математике Параллелепипед, призма, пирамида (9 класс)
- 2. Здравствуйте дорогие ребята и гости урока!
- 3. Параллелепипед,Призма, пирамидаТема урока:
- 4. Цель урока:Повторить полученные знания по теме:«Параллелепипед, призма, пирамида»
- 5. Задание 1. Из изображенных фигур исключить лишнюю фигуру
- 6. Задание 2. Какая из шести фигур должна оказаться в свободной клеточке?
- 7. Задание 3.Сравнивая, выявляя закономерность в рядах, из шести пронумерованных фигур, выбрать нужную фигуру.
- 8. Теория многогранников, в частности выпуклых
- 9. Сегодняшний урок посвящен увлекательному разделу геометрии –
- 10. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ Пифагор и его ученики считали,
- 11. Понятие многогранника Что такое многогранник?
- 12. Стороны и вершины граней называют
- 13. ПРИЗМАПризмой называется многогранник,поверхность которого состоит из двух
- 14. КУБ, ПАРАЛЛЕЛЕПИПЕДПараллелепипедом называется многогранник,поверхность которого состоит из
- 15. ПИРАМИДАПирамидой называется многогранник,поверхность которого состоит из многоугольника,
- 16. ФИЗМИНУТКА
- 17. КРОССВОРД
- 18. По горизонтали:1.Призма, в основании которой лежит параллелограмм.2.Прямоугольный
- 19. Ответы к кроссворду:1.Параллелепипед2.Куб3.Призма4.Апофема5.Пряпоугольник6.Квадрат7.Пирамида8.Хеопса9.Восемь10.Диагональ
- 20. Домашнее задание Повторить теорию. Задание: найти площадь
- 21. Я хочу закончить наш урок словами французского
- 22. Слайд 22
Слайд 7Задание 3.Сравнивая, выявляя закономерность в рядах, из шести пронумерованных фигур, выбрать
Слайд 8 Теория многогранников, в частности выпуклых многогранников – одна из
Слайд 9Сегодняшний урок посвящен увлекательному разделу геометрии – теории многогранников.
Чем привлекательны многогранники?
Достаточно вспомнить знаменитые египетские пирамиды и самую известную из них – пирамиду Хеопса. Это правильная пирамида, в основании которой квадрат со стороной 233 м и высота которой достигает 146,5 м.
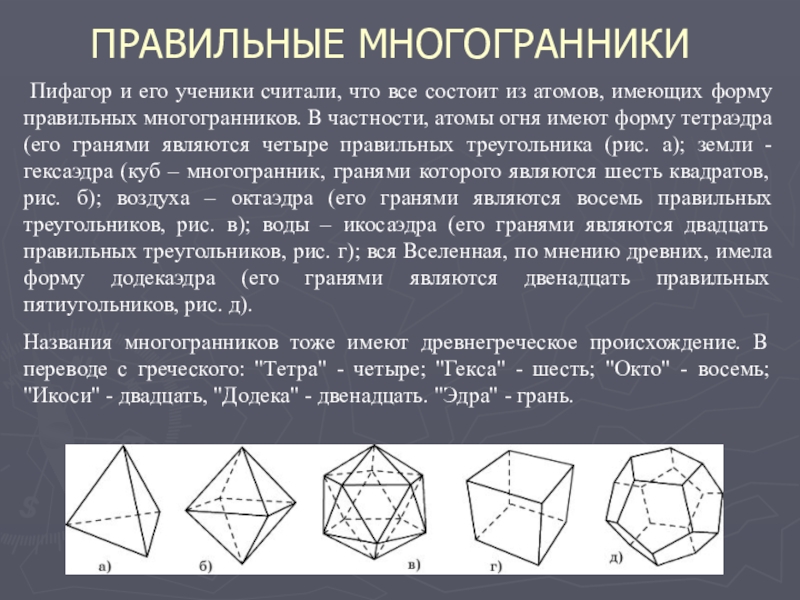
Слайд 10ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
Пифагор и его ученики считали, что все состоит из
Названия многогранников тоже имеют древнегреческое происхождение. В переводе с греческого: "Тетра" - четыре; "Гекса" - шесть; "Окто" - восемь; "Икоси" - двадцать, "Додека" - двенадцать. "Эдра" - грань.
Слайд 11Понятие многогранника
Что такое многогранник?
Большой класс геометрических тел
С чисто геометрической точки зрения многогранник – это часть пространства, ограниченная плоскими многоугольниками.
Слайд 12 Стороны и вершины граней называют ребрами и вершинами самого
ОПРЕДЕЛЕНИЕ: Многогранник называется выпуклым, если он лежит по одну сторону от плоскости любой из его граней.
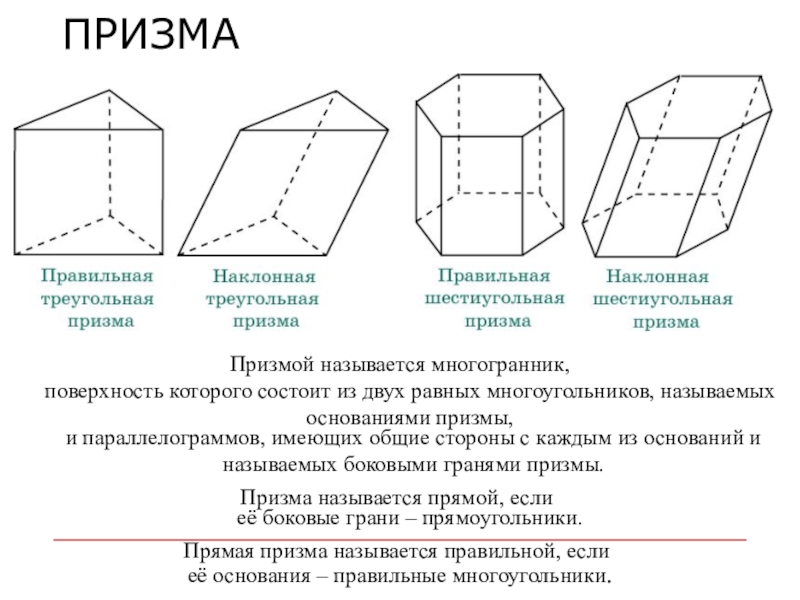
Слайд 13ПРИЗМА
Призмой называется многогранник,
поверхность которого состоит из двух равных многоугольников, называемых основаниями
и параллелограммов, имеющих общие стороны с каждым из оснований и называемых боковыми гранями призмы.
Призма называется прямой, если
её боковые грани – прямоугольники.
Прямая призма называется правильной, если
её основания – правильные многоугольники.
Слайд 14КУБ, ПАРАЛЛЕЛЕПИПЕД
Параллелепипедом называется многогранник,
поверхность которого состоит из шести параллелограммов.
Прямоугольным параллелепипедом называется
грани которого – прямоугольники.
Кубом называется многогранник,
поверхность которого состоит из шести квадратов.
Слайд 15ПИРАМИДА
Пирамидой называется многогранник,
поверхность которого состоит из многоугольника, называемого
основанием пирамиды, и
треугольников, имеющих
боковыми гранями пирамиды.
Пирамида называется правильной, если
её основание – правильный многоугольник и
все боковые ребра равны.
Слайд 18По горизонтали:
1.Призма, в основании которой лежит параллелограмм.
2.Прямоугольный параллелепипед с равными измерениями.
3.Многогранник,
4.Как называется высота боковой грани правильной пирамиды с концом в ее вершине.
5.Прямоугольным называется параллелепипед, у которого каждая грань представляет собой……
По вертикали:
6.Все грани куба представляют собой…
7.Многогранник, у которого одна грань – какой – либо многоугольник, а остальные грани – треугольники с общей вершиной.
8.Как называется самая большая пирамида.
9. Сколько вершин у прямоугольного параллелепипеда.
10.Отрезок, соединяющий вершины двух оснований призмы и не лежащий внутри нее.
Слайд 19Ответы к кроссворду:
1.Параллелепипед
2.Куб
3.Призма
4.Апофема
5.Пряпоугольник
6.Квадрат
7.Пирамида
8.Хеопса
9.Восемь
10.Диагональ
Слайд 20Домашнее задание
Повторить теорию. Задание: найти площадь поверхности любых предметов, которые
№ 275, № 277. учебника геометрии 9кл. И.Бекбоев, К.Кайдасов