Презентация, доклад по математике Основные понятия геометрии

Содержание

1. Презентация по математике Основные понятия геометрии
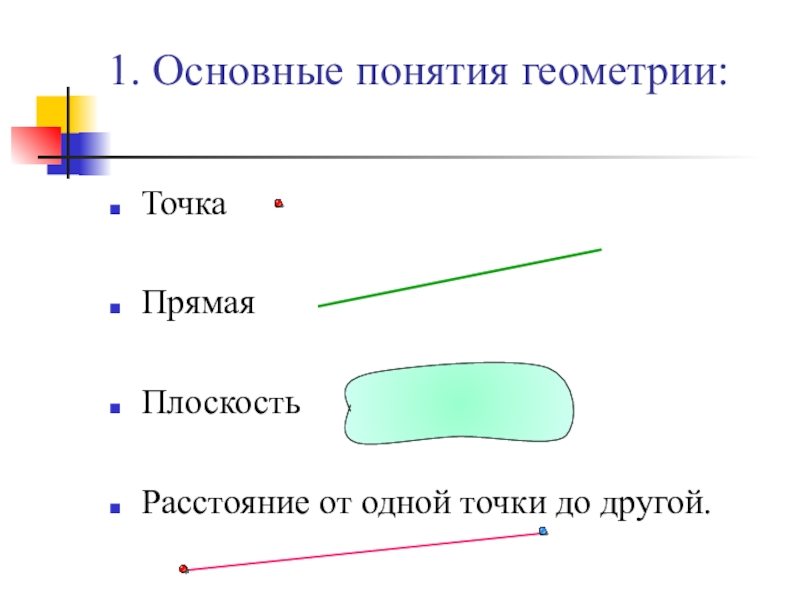
2. ТочкаПрямаяПлоскостьРасстояние от одной точки до другой.1. Основные понятия геометрии:
3. АВПлоскость и прямая состоят из точек.Существуют точки
4. 2. Взаимное расположение прямых на плоскости.1 случай:
5. Докажем, что прямые a и b могут
6. Отрезок – это часть прямой, ограниченная двумя
7. ВСАДва отрезка называются пересекающимися, если они имеют
8. ОА – луч; О – начало лучаO4.
9. Противоположные лучи.Лучи называются противоположными (дополнительными), если:Они принадлежат
10. Сколько точек пересечения могут иметь 3 прямые?
11. На плоскости даны 3 точки. Сколько прямых
12. В5. УголУгол – это геометрическая фигура, состоящая
13. ОКак обозначают углы.СDhkA
14. ОУгол, стороны которого являются противоположными лучами, называется развернутым.АВЛучи ОА и ОВ - противоположные
15. KFEРСВАЛюбой угол разделяет плоскость на две части.Если
16. EЕсли луч исходит из вершины угла и

ТочкаПрямаяПлоскостьРасстояние от одной точки до другой.1. Основные понятия геометрии:

Главная
Геометрия
Презентация по математике Основные понятия геометрии

Слайд 1Основные понятия
геометрии

Слайд 2Точка

Прямая

Плоскость

Расстояние от одной точки до другой.
1. Основные понятия геометрии:

Слайд 3А
В
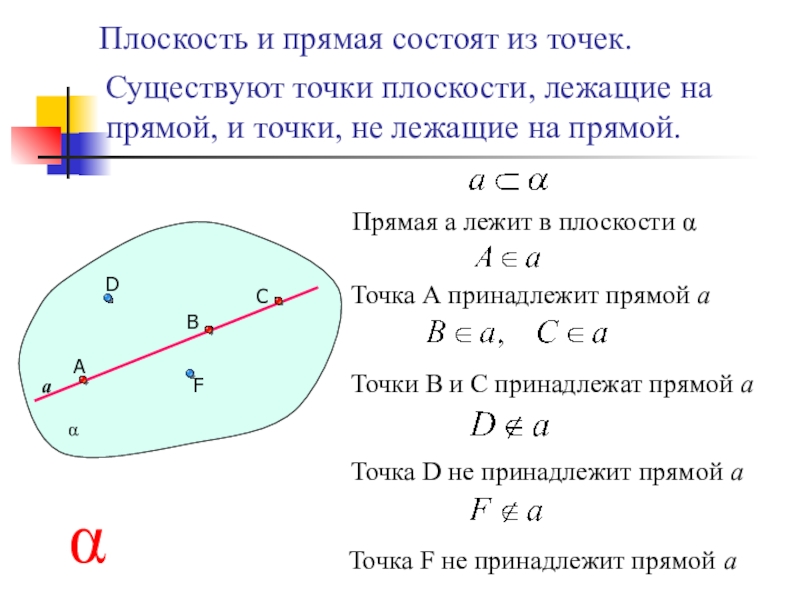
Плоскость и прямая состоят из точек.
Существуют точки плоскости, лежащие на прямой,

и точки, не лежащие на прямой.

Прямая а лежит в плоскости α

Точка А принадлежит прямой а

Точка D не принадлежит прямой а

Точки В и С принадлежат прямой а

Точка F не принадлежит прямой а

АВПлоскость и прямая состоят из точек.Существуют точки плоскости, лежащие на прямой, и точки, не лежащие на прямой.ααаСDFПрямая

Слайд 42. Взаимное расположение прямых на плоскости.
1 случай:
Прямые не имеют общих

точек (т.е. параллельны)

2 случай:
Прямые имеют 1 общую точку (т.е. пересекаются)

Прямая а пересекает прямую b в точке М

2. Взаимное расположение прямых на плоскости.1 случай: Прямые не имеют общих точек (т.е. параллельны)аb2 случай: Прямые имеют

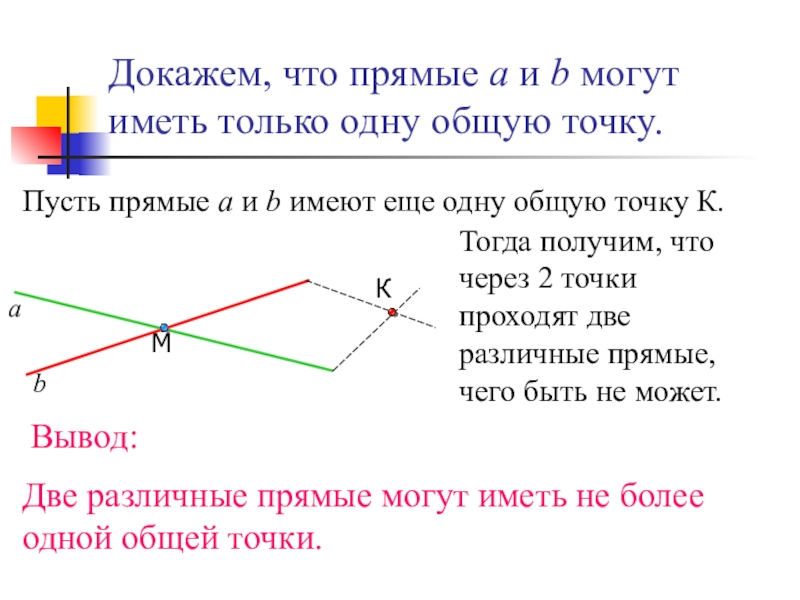
Слайд 5Докажем, что прямые a и b могут иметь только одну общую

точку.

Пусть прямые а и b имеют еще одну общую точку К.

Тогда получим, что через 2 точки проходят две различные прямые, чего быть не может.

Вывод:

Две различные прямые могут иметь не более одной общей точки.

Докажем, что прямые a и b могут иметь только одну общую точку.МПусть прямые а и b имеют

Слайд 6Отрезок – это часть прямой, ограниченная двумя точками этой прямой.
В
3. Отрезок.
А
а
Эти

точки называются концами отрезка.

Точки, лежащие между концами отрезка называются внутренними.

Слайд 7В
С
А
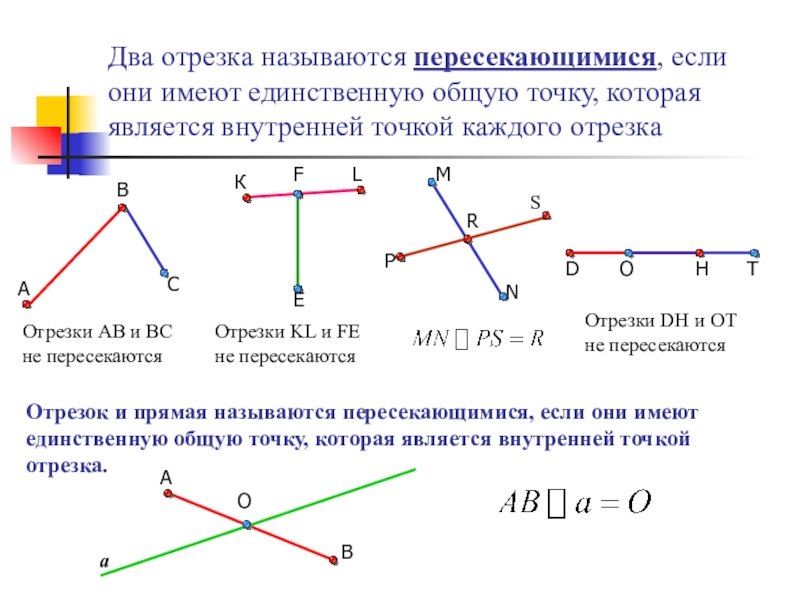
Два отрезка называются пересекающимися, если они имеют единственную общую точку, которая

является внутренней точкой каждого отрезка

Отрезки АВ и ВС не пересекаются

Отрезки KL и FE не пересекаются

Отрезки DH и OT не пересекаются

Отрезок и прямая называются пересекающимися, если они имеют единственную общую точку, которая является внутренней точкой отрезка.

ВСАДва отрезка называются пересекающимися, если они имеют единственную общую точку, которая является внутренней точкой каждого отрезкаВКLFEMNPSRDOHTОтрезки АВ

Слайд 8ОА – луч; О – начало луча
O
4. Луч.
а
А
Лучом называется часть прямой,

ограниченная точкой этой прямой.

Отрезок и луч называются пересекающимися, если их единственная общая точка не совпадает с началом луча и является внутренней точкой отрезка.

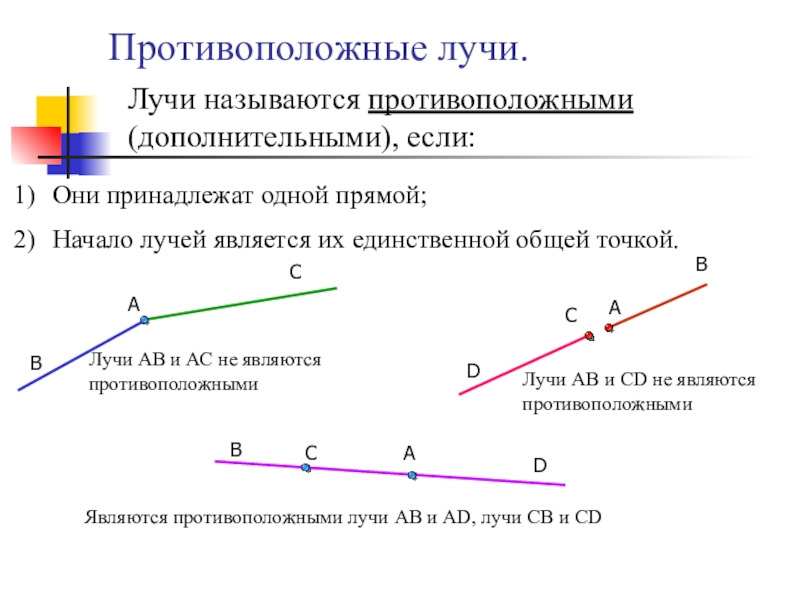
Слайд 9Противоположные лучи.
Лучи называются противоположными (дополнительными), если:
Они принадлежат одной прямой;
Начало лучей является

их единственной общей точкой.

Лучи АВ и АС не являются противоположными

Лучи АВ и СD не являются противоположными

Являются противоположными лучи АВ и AD, лучи СВ и CD

Противоположные лучи.Лучи называются противоположными (дополнительными), если:Они принадлежат одной прямой;Начало лучей является их единственной общей точкой.Лучи АВ и

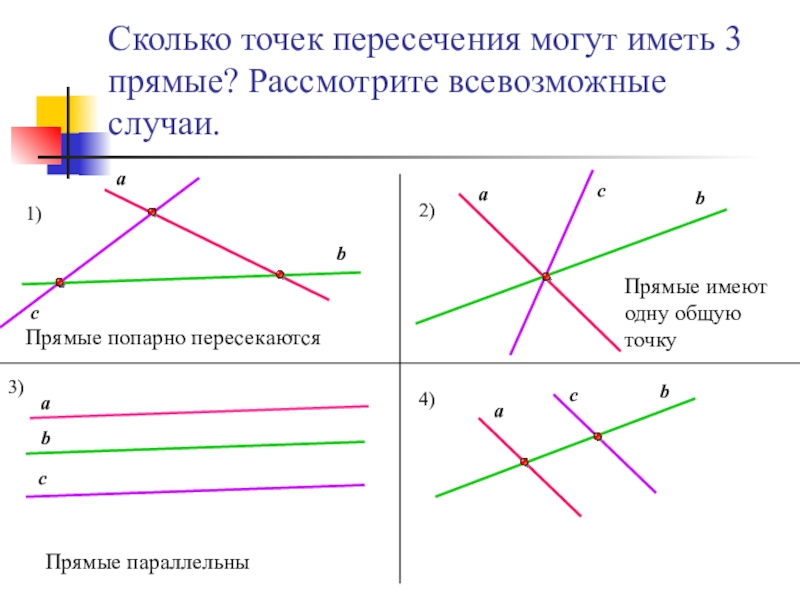
Слайд 10Сколько точек пересечения могут иметь 3 прямые? Рассмотрите всевозможные случаи.
Прямые попарно

пересекаются

Прямые имеют одну общую точку

Прямые параллельны

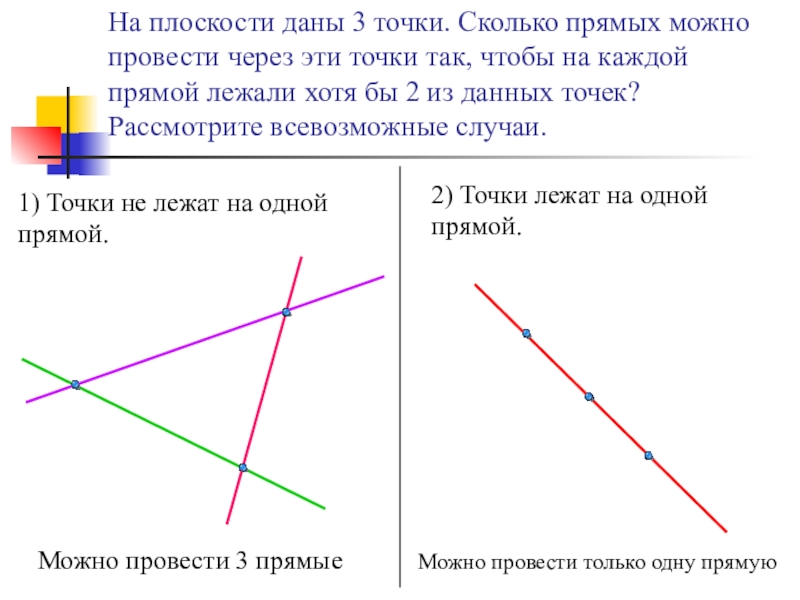
Слайд 11На плоскости даны 3 точки. Сколько прямых можно провести через эти

точки так, чтобы на каждой прямой лежали хотя бы 2 из данных точек? Рассмотрите всевозможные случаи.

1) Точки не лежат на одной прямой.

2) Точки лежат на одной прямой.

Можно провести 3 прямые

Можно провести только одну прямую

На плоскости даны 3 точки. Сколько прямых можно провести через эти точки так, чтобы на каждой прямой

Слайд 12В
5. Угол
Угол – это геометрическая фигура, состоящая из точки и двух

лучей, исходящих из этой точки.

Лучи называются сторонами угла.
Их начало – вершиной угла.

ВА и ВС – стороны угла АВС,
Точка В – вершина угла АВС

В5. УголУгол – это геометрическая фигура, состоящая из точки и двух лучей, исходящих из этой точки.Лучи называются

Слайд 13О
Как обозначают углы.
С
D
h
k
A

Слайд 14О
Угол, стороны которого являются противоположными лучами, называется развернутым.
А
В
Лучи ОА и ОВ

- противоположные

Слайд 15K
F
E
Р
С
В
А
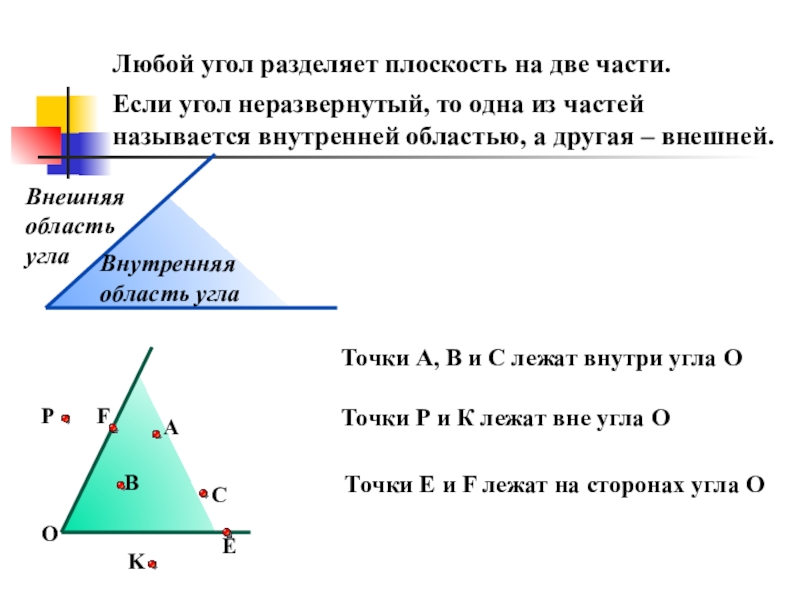
Любой угол разделяет плоскость на две части.
Если угол неразвернутый, то одна

из частей называется внутренней областью, а другая – внешней.

Внешняя область угла

Внутренняя область угла

Точки А, В и С лежат внутри угла О

Точки Р и К лежат вне угла О

Точки Е и F лежат на сторонах угла О

KFEРСВАЛюбой угол разделяет плоскость на две части.Если угол неразвернутый, то одна из частей называется внутренней областью, а

Слайд 16E
Если луч исходит из вершины угла и проходит внутри угла, то

он делит этот угол на два угла.

Луч ОС делит угол АОВ на два угла: АОС и ВОС

Неразвернутый угол

Развернутый угол

Луч ОE делит угол АОВ на два угла: АОС и ВОС

EЕсли луч исходит из вершины угла и проходит внутри угла, то он делит этот угол на два

Скачать презентацию

Презентация, доклад по математике Основные понятия геометрии

Содержание

Слайд 1Основные понятия
геометрии

Слайд 2Точка

Прямая

Плоскость

Расстояние от одной точки до другой.
1. Основные понятия геометрии:

Слайд 3А
В
Плоскость и прямая состоят из точек.
Существуют точки плоскости, лежащие на прямой,

Слайд 42. Взаимное расположение прямых на плоскости.
1 случай:
Прямые не имеют общих

Слайд 5Докажем, что прямые a и b могут иметь только одну общую

Слайд 6Отрезок – это часть прямой, ограниченная двумя точками этой прямой.
В
3. Отрезок.
А
а
Эти

Слайд 7В
С
А
Два отрезка называются пересекающимися, если они имеют единственную общую точку, которая

Слайд 8ОА – луч; О – начало луча
O
4. Луч.
а
А
Лучом называется часть прямой,

Слайд 9Противоположные лучи.
Лучи называются противоположными (дополнительными), если:
Они принадлежат одной прямой;
Начало лучей является

Слайд 10Сколько точек пересечения могут иметь 3 прямые? Рассмотрите всевозможные случаи.
Прямые попарно

Слайд 11На плоскости даны 3 точки. Сколько прямых можно провести через эти

Слайд 12В
5. Угол
Угол – это геометрическая фигура, состоящая из точки и двух

Слайд 13О
Как обозначают углы.
С
D
h
k
A

Слайд 14О
Угол, стороны которого являются противоположными лучами, называется развернутым.
А
В
Лучи ОА и ОВ

Слайд 15K
F
E
Р
С
В
А
Любой угол разделяет плоскость на две части.
Если угол неразвернутый, то одна

Слайд 16E
Если луч исходит из вершины угла и проходит внутри угла, то

Что такое shareslide.ru?

Обратная связь

Презентация, доклад по математике Основные понятия геометрии

Содержание

Слайд 1Основные понятиягеометрии

Слайд 2ТочкаПрямаяПлоскостьРасстояние от одной точки до другой.1. Основные понятия геометрии:

Слайд 3АВПлоскость и прямая состоят из точек.Существуют точки плоскости, лежащие на прямой,

Слайд 42. Взаимное расположение прямых на плоскости.1 случай: Прямые не имеют общих

Слайд 5Докажем, что прямые a и b могут иметь только одну общую

Слайд 6Отрезок – это часть прямой, ограниченная двумя точками этой прямой.В3. Отрезок.АаЭти

Слайд 7ВСАДва отрезка называются пересекающимися, если они имеют единственную общую точку, которая

Слайд 8ОА – луч; О – начало лучаO4. Луч.аАЛучом называется часть прямой,

Слайд 9Противоположные лучи.Лучи называются противоположными (дополнительными), если:Они принадлежат одной прямой;Начало лучей является

Слайд 10Сколько точек пересечения могут иметь 3 прямые? Рассмотрите всевозможные случаи.Прямые попарно

Слайд 11На плоскости даны 3 точки. Сколько прямых можно провести через эти

Слайд 12В5. УголУгол – это геометрическая фигура, состоящая из точки и двух

Слайд 13ОКак обозначают углы.СDhkA

Слайд 14ОУгол, стороны которого являются противоположными лучами, называется развернутым.АВЛучи ОА и ОВ

Слайд 15KFEРСВАЛюбой угол разделяет плоскость на две части.Если угол неразвернутый, то одна

Слайд 16EЕсли луч исходит из вершины угла и проходит внутри угла, то

Похожие презентации

Что такое shareslide.ru?

Обратная связь

Слайд 1Основные понятия
геометрии

Слайд 2Точка

Прямая

Плоскость

Расстояние от одной точки до другой.
1. Основные понятия геометрии:

Слайд 3А
В
Плоскость и прямая состоят из точек.
Существуют точки плоскости, лежащие на прямой,

Слайд 42. Взаимное расположение прямых на плоскости.
1 случай:
Прямые не имеют общих

Слайд 6Отрезок – это часть прямой, ограниченная двумя точками этой прямой.
В
3. Отрезок.
А
а
Эти

Слайд 7В
С
А
Два отрезка называются пересекающимися, если они имеют единственную общую точку, которая

Слайд 8ОА – луч; О – начало луча
O
4. Луч.
а
А
Лучом называется часть прямой,

Слайд 9Противоположные лучи.
Лучи называются противоположными (дополнительными), если:
Они принадлежат одной прямой;
Начало лучей является

Слайд 10Сколько точек пересечения могут иметь 3 прямые? Рассмотрите всевозможные случаи.
Прямые попарно

Слайд 12В
5. Угол
Угол – это геометрическая фигура, состоящая из точки и двух

Слайд 13О
Как обозначают углы.
С
D
h
k
A

Слайд 14О
Угол, стороны которого являются противоположными лучами, называется развернутым.
А
В
Лучи ОА и ОВ

Слайд 15K
F
E
Р
С
В
А
Любой угол разделяет плоскость на две части.
Если угол неразвернутый, то одна

Слайд 16E
Если луч исходит из вершины угла и проходит внутри угла, то