2018
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Окружность
Содержание
- 1. Презентация по математике Окружность
- 2. Основные факты по теме «Окружность и
- 3. Основные факты по теме «Окружность и
- 4. Основные факты по теме «Окружность и круг»
- 5. Основные факты по теме «Окружность и круг»
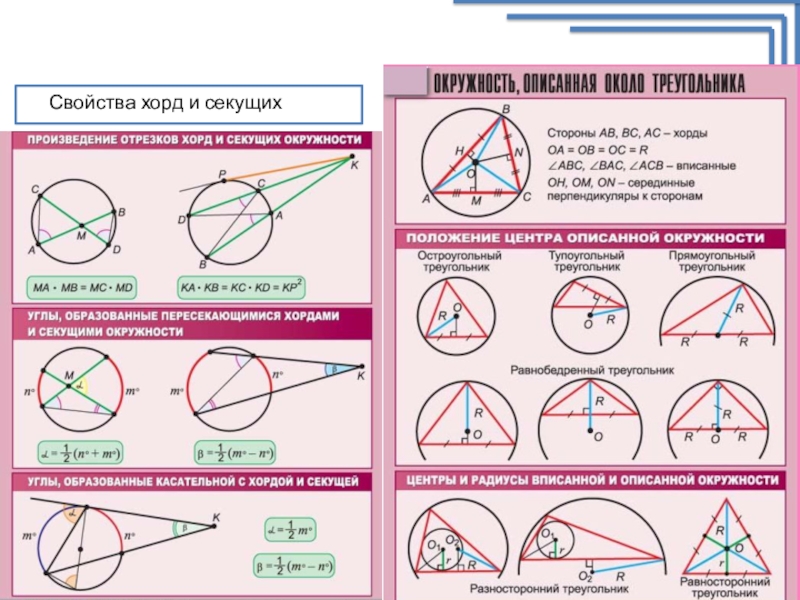
- 6. Окружность, хорды и касательныеСвойства хорд и секущих
- 7. Центральные и вписанные углыВписанные и описанные четырехугольники
- 8. Свойства хорд и секущих
- 9.
- 10.
- 11. Пример 1. Окружность пересекает стороны угла
- 12. Пример 3.Решение. Рассмотрим треугольник ВОС.
- 13. Пример 4.Решение.∠АВС = ∠АВD + ∠DВС,
- 14. Пример 5Решение. Чтобы решить эту задачу
- 15. Пример 6Решение. ∠NMB опирается на дугу
- 16. Пример 7Решение. Центральный угол АОС опирается
Слайд 1
Окружность.
ГБПОУ ВО «Павловский техникум»
Автор презентации – учитель математики Северинов
Слайд 2
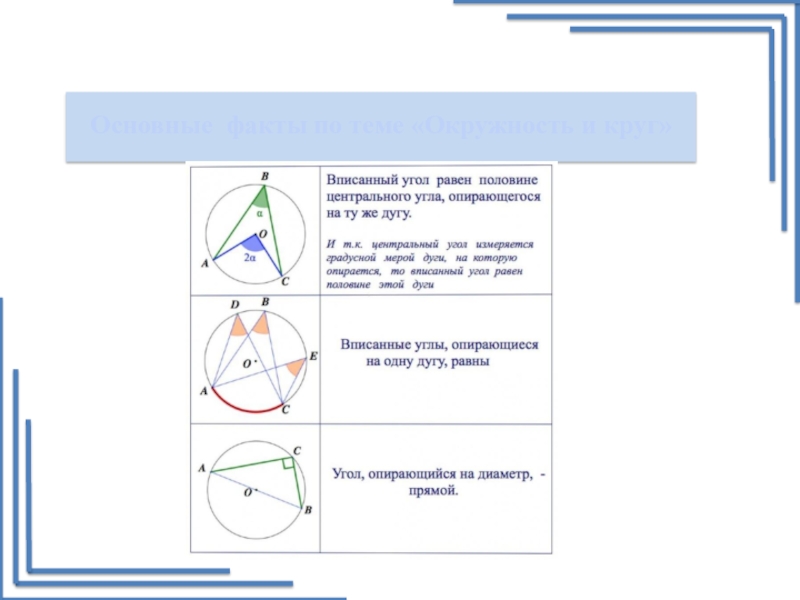
Основные факты по теме «Окружность и круг»
. Рассмотрим примеры решения
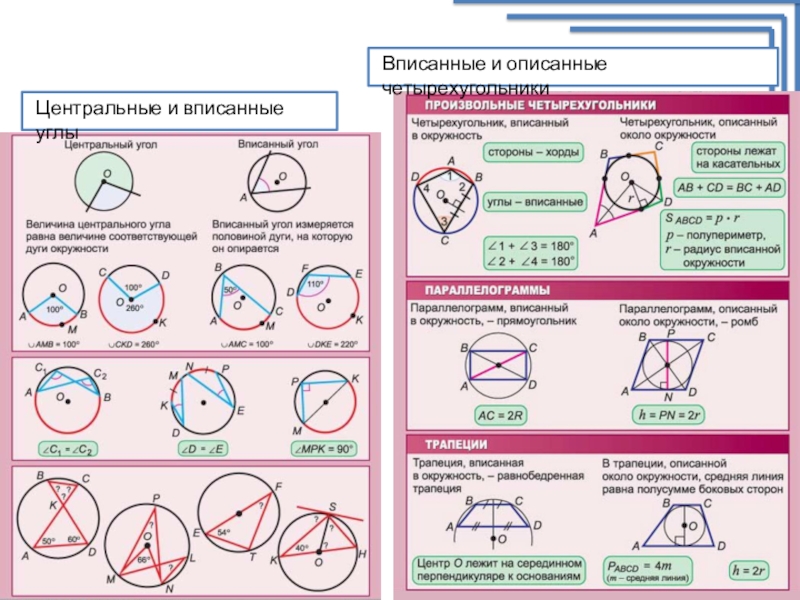
• центральный угол равен дуге окружности, на которую он опирается;
• вписанный угол окружности равен половине центрального угла
и измеряется половиной дуги, на которую он опирается;
• вписанный угол, опирающийся на диаметр окружности, равен 90◦;
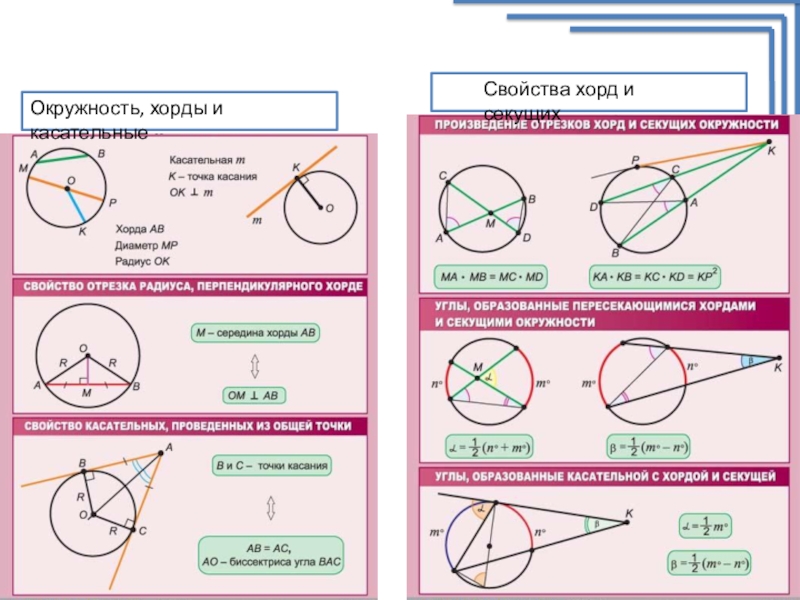
• касательная к окружности перпендикулярна к радиусу этой окружности, проведённому в точку касания;
• отрезки касательных, проведённых к окружности из одной точки, равны;
Слайд 3
Основные факты по теме «Окружность и круг»
• центр окружности, вписанной
• угол между двумя секущими к окружности, пересекающимися внутри окружности, равен полусумме дуг, высекаемых на окружности вертикальными углами, образованными этими секущими;
• угол между двумя секущими к окружности, пересекающимися вне окружности, равен полуразности дуг, высекаемых на окружности углом, образованным этими секущими;
• две окружности имеют ровно две общие точки (пересекаются в двух точках) в том и только том случае, если расстояние между их центрами меньше суммы радиусов этих окружностей, но больше разности большего и меньшего радиусов;
• две окружности имеют ровно одну общую точку (касаются) в том
и только том случае, если расстояние между их центрами равно сумме
радиусов этих окружностей (внешнее касание) либо равно разности
большего и меньшего радиусов этих окружностей (внутреннее касание);
• формула длины окружности , где r—радиус окружности;
• формула площади круга , где r—радиус круга.
Слайд 11
Пример 1. Окружность пересекает стороны угла величиной 33◦
с вершиной C
на рисунке. Найдите угол ADB, если угол EAD равен 22◦.
Ответ дайте в градусах.
Решение. Рассмотрим треугольник ACD. Угол ADB является для него внешним при вершине D, значит, он равен сумме двух других углов треугольника, не смежных с ним:
Ответ: 55.
Пример 2. Точки А, В, С и D, последовательно расположенные на окружности в указанном порядке, делят ее на четыре дуги, градусные меры которых относятся как 1:2:7:8 (дуга АВ – наименьшая). Найдите градусную меру дуги ВD, содержащей точку С.
Слайд 12
Пример 3.
Решение. Рассмотрим треугольник ВОС. ВО=ОС=R, следовательно, треугольник ВОС
∠ОСВ = ∠ОВС =
∠АОD = ∠ВОС (как вертикальные),
∠АОD = ∠ВОС= 180 – 38*2=180-76=104.
Ответ: 104.
Слайд 13
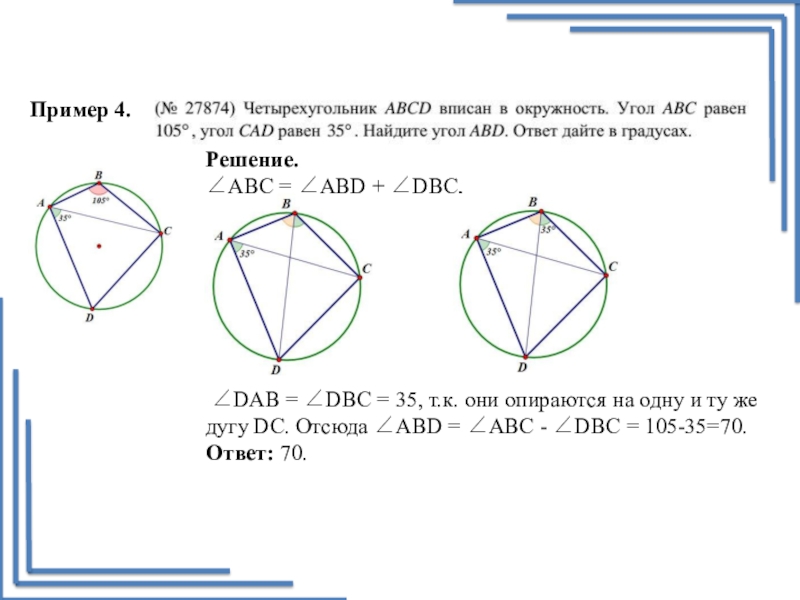
Пример 4.
Решение.
∠АВС = ∠АВD + ∠DВС,
∠DАВ = ∠DВС =
Ответ: 70.
Слайд 14
Пример 5
Решение. Чтобы решить эту задачу нам нужно вспомнить два
1. Вписанный угол, который опирается на диаметр , равен . И наоборот, если вписанный угол равен , то он опирается на диаметр. Следовательно, гипотенуза АВ прямоугольного треугольника АВС является диаметром описанной около треугольника окружности, то есть
2. центр описанной около прямоугольного треугольника окружности совпадает с серединой гипотенузы. Найдем по теореме Пифагора гипотенузу АВ Отсюда АВ = 5, тогда R=2,5.
Ответ: 2,5.
Слайд 15
Пример 6
Решение. ∠NMB опирается на дугу NB. Найдем величину этой
Ответ: 54.
Слайд 16
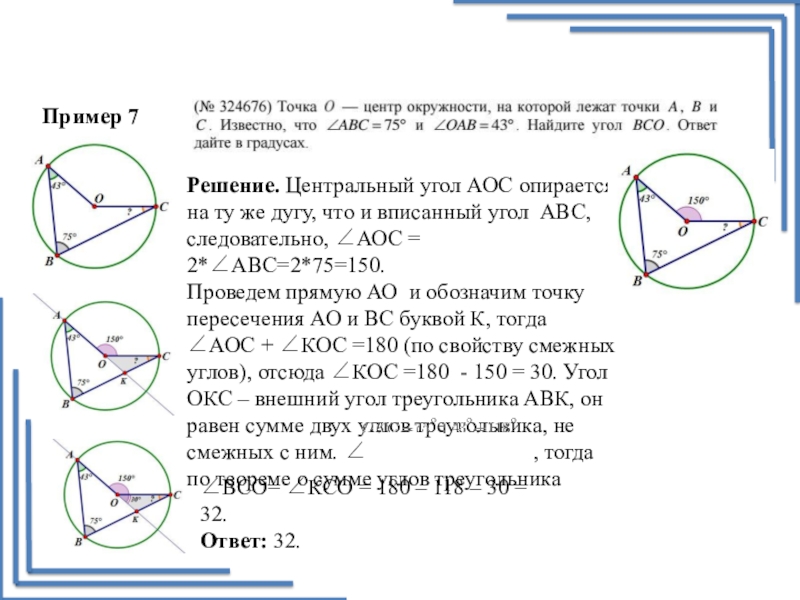
Пример 7
Решение. Центральный угол АОС опирается на ту же дугу,
Проведем прямую АО и обозначим точку пересечения АО и ВС буквой К, тогда
∠АОС + ∠КОС =180 (по свойству смежных углов), отсюда ∠КОС =180 - 150 = 30. Угол ОКС – внешний угол треугольника АВК, он равен сумме двух углов треугольника, не смежных с ним. ∠ , тогда по теореме о сумме углов треугольника
∠ВСО= ∠КСО = 180 – 118 – 30 = 32.
Ответ: 32.