- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад ПО МАТЕМАТИКЕ НА ТЕМУОКРУЖНОСТЬ11 КЛАСС ПОВТОРЕНИЕ
Содержание
- 1. ПРЕЗЕНТАЦИЯ ПО МАТЕМАТИКЕ НА ТЕМУОКРУЖНОСТЬ11 КЛАСС ПОВТОРЕНИЕ
- 2. Один мудрец сказал: « Высшее проявление духа
- 3. ЦЕЛЬ УРОКА: Систематизировать знания и умения по
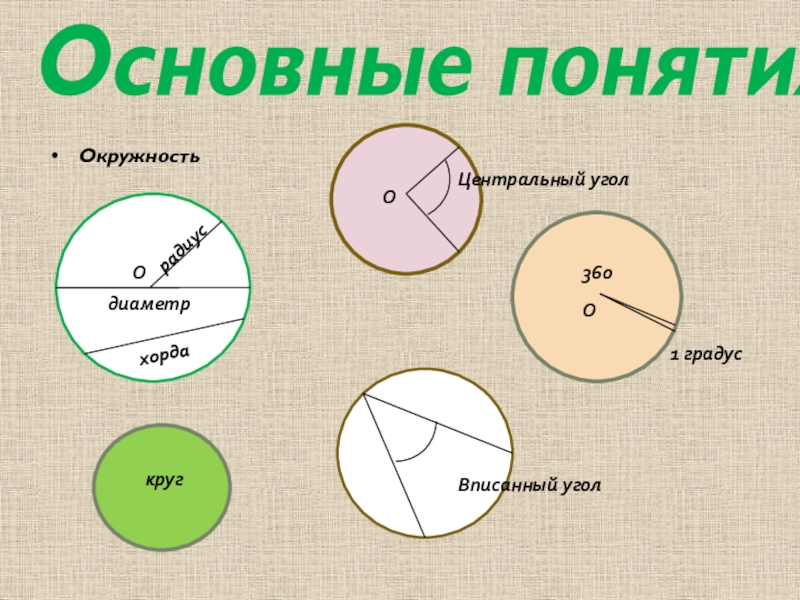
- 4. Основные понятияОкружностьрадиусдиаметрхордакругЦентральный уголВписанный угол1 градус360ООО
- 5. Нет общих точекОдна общая точкаДве общие точкиЛюбая
- 6. Окружность и углы
- 7. Центральные углы АОВСД 1. Градусная
- 8. Теорема о вписанных углахООО
- 9. Углы, вписанные в окружность2. Вписанные углы, опирающиеся
- 10. Углы между секущими
- 11. Угол между касательной и хордойАКМДМКОЕАУгол между
- 12. Параллельные хорды заключают равные дуги.
- 13. Свойство секущих к окружностиЕсли из одной точки
- 14. Окружность и касательные
- 15. Свойства касательных к окружности
- 16. Окружность и треугольник
- 17. Определение. Многоугольник называется вписанным в окружность,
- 18. Центром окружности, описанной около треугольника, является точка
- 19. Определение. Окружность вписана в треугольник,
- 20. Четырехугольники и окружность
- 21. Вписанные четырехугольникиКвадратПрямоугольник Равнобедренная
- 22. Окружность, вписанная в четырехугольникОпределение. Окружность называется вписанной
- 23. Окружность в задачах ЕГЭ В окружности проведены
- 24. Окружность в задачах ЕГЭ В окружности проведены
- 25. Окружность в задачах ЕГЭ В окружности проведены
- 26. Молодец!!!
Слайд 2Один мудрец сказал: « Высшее проявление духа – это разум.
Высшее проявление
Клетка геометрии – треугольник. Он так же неисчерпаем, как и Вселенная.
Окружность – душа геометрии.
Познайте окружность, и вы не только познаете душу геометрии, но и возвысите душу свою.
Слайд 3ЦЕЛЬ УРОКА: Систематизировать знания и умения по теме окружность. Выработать навыки
Слайд 5
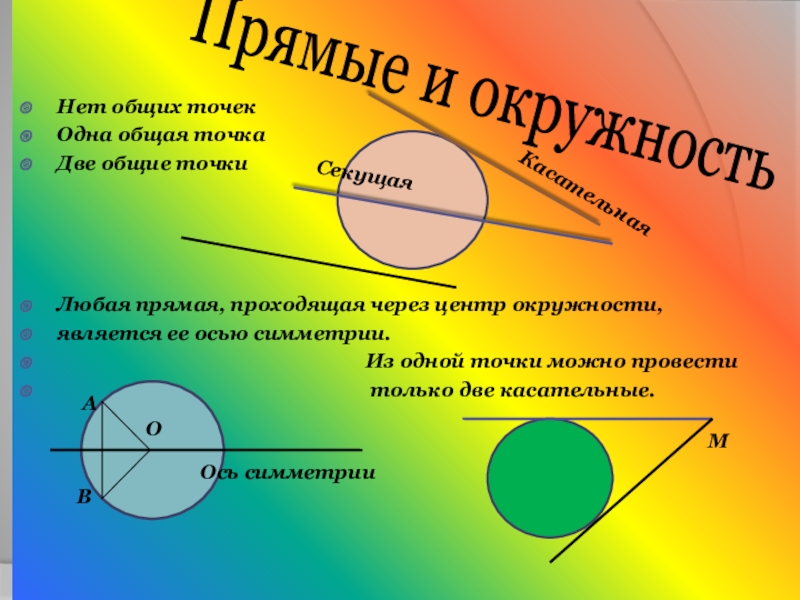
Нет общих точек
Одна общая точка
Две общие точки
Любая прямая, проходящая через центр
является ее осью симметрии.
Из одной точки можно провести
только две касательные.
Прямые и окружность
Касательная
Секущая
Ось симметрии
О
А
В
М
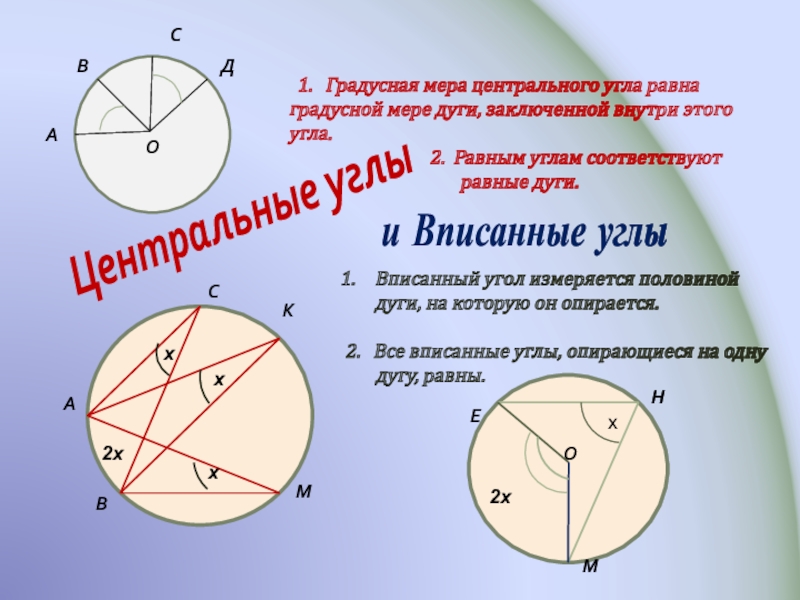
Слайд 7Центральные углы
А
О
В
С
Д
1. Градусная мера центрального угла равна
2. Равным углам соответствуют
равные дуги.
и Вписанные углы
Вписанный угол измеряется половиной дуги, на которую он опирается.
2. Все вписанные углы, опирающиеся на одну
дугу, равны.
А
Е
М
О
Н
В
С
К
М
х
х
х
2х
2х
х
Слайд 9Углы, вписанные в окружность
2. Вписанные углы, опирающиеся на диаметр, являются прямыми.
Сумма
180 градусам .
180
90
О
А
В
С
Д
N
F
S
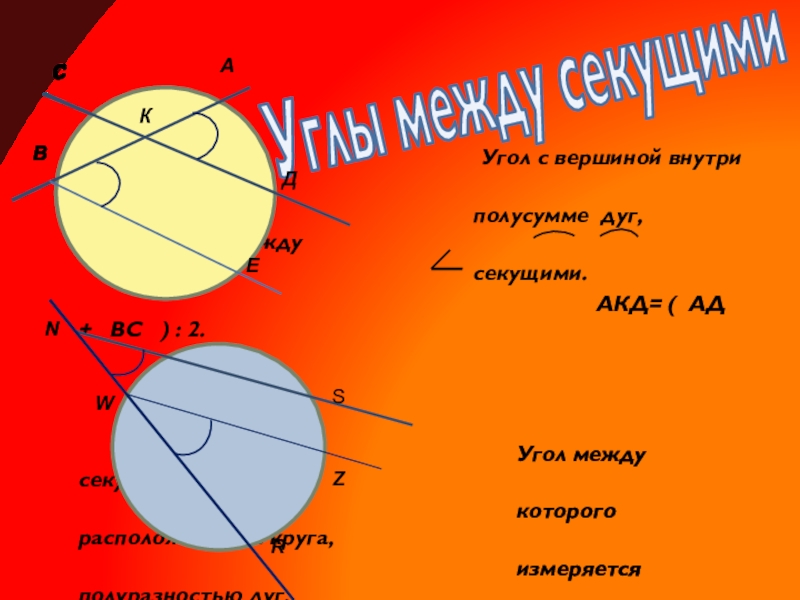
Слайд 10Углы между секущими
полусумме дуг, заключенных между
секущими.
АКД= ( АД + ВС ) : 2.
Угол между секущими, вершина
которого расположена вне круга,
измеряется полуразностью дуг,
заключенных внутри угла.
А
В
С
Д
Е
N
S
R
Z
W
К
Слайд 11
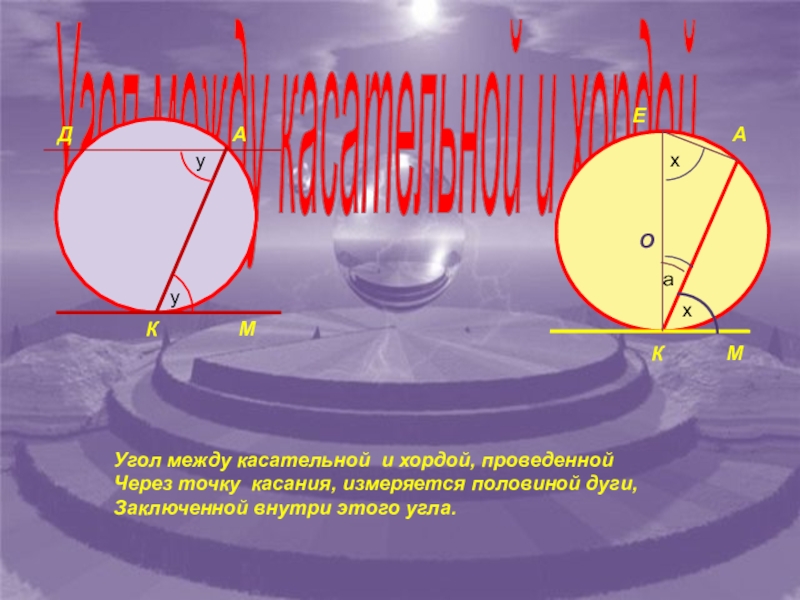
Угол между касательной и хордой
А
К
М
Д
М
К
О
Е
А
Угол между касательной и хордой, проведенной
Через
Заключенной внутри этого угла.
х
х
у
у
а
Слайд 12
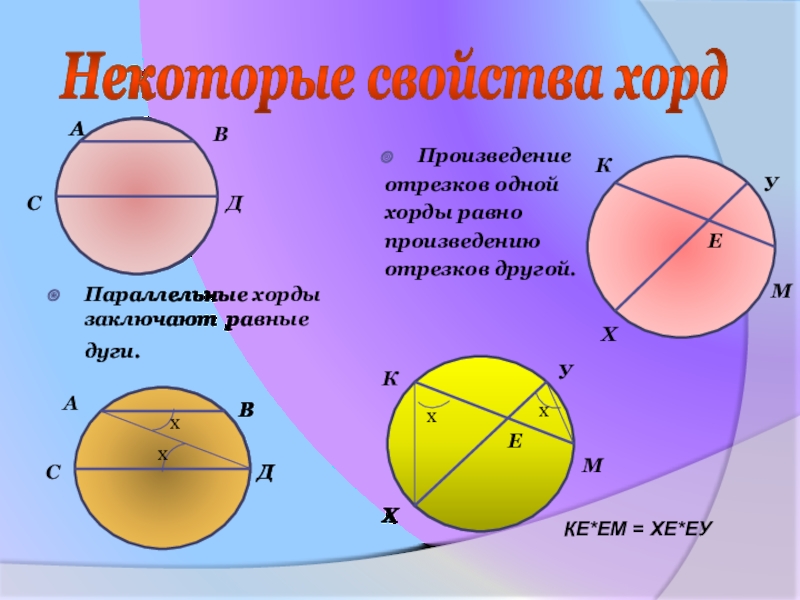
Параллельные хорды заключают равные дуги.
Произведение
отрезков одной
хорды равно
произведению
отрезков другой.
Некоторые свойства хорд
А
В
С
Д
К
М
Х
У
Е
А
В
С
Д
К
М
У
Х
Е
х
х
х
х
КЕ*ЕМ = ХЕ*ЕУ
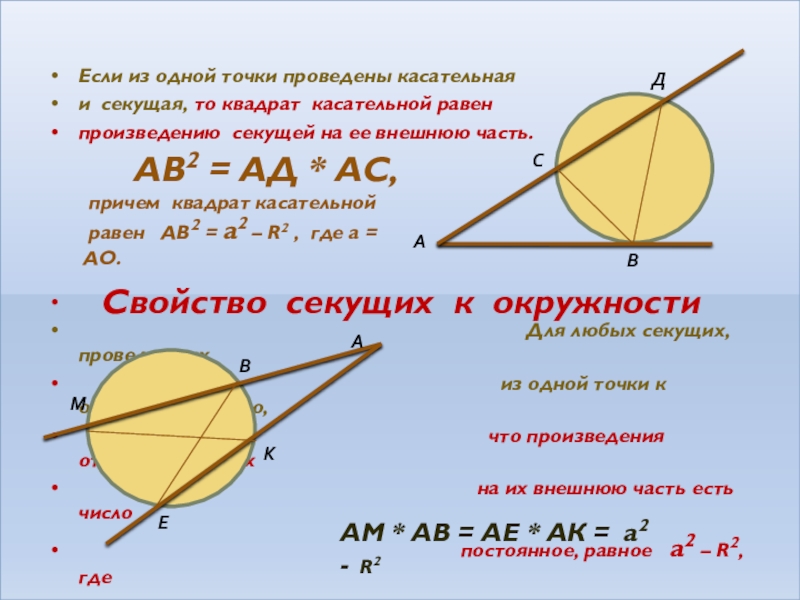
Слайд 13Свойство секущих к окружности
Если из одной точки проведены касательная
и секущая,
произведению секущей на ее внешнюю часть.
Для любых секущих, проведенных
из одной точки к окружности, верно,
что произведения отрезков секущих
на их внешнюю часть есть число
постоянное, равное а2 – R2,где
а – расстояние от центра до точки А.
А
В
С
Д
АВ2 = АД * АС,
причем квадрат касательной
равен АВ2 = а2 – R2 , где а = АО.
А
В
М
К
Е
АМ * АВ = АЕ * АК = а2 - R2
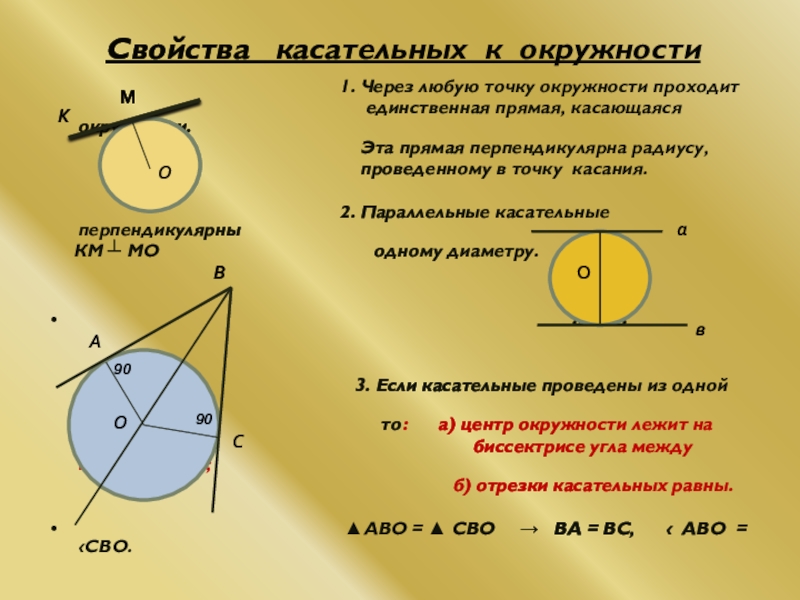
Слайд 15Свойства касательных к окружности
единственная прямая, касающаяся окружности.
Эта прямая перпендикулярна радиусу,
проведенному в точку касания.
2. Параллельные касательные перпендикулярны
КМ ┴ МО одному диаметру.
а // в
3. Если касательные проведены из одной точки,
то: а) центр окружности лежит на
биссектрисе угла между касательными;
б) отрезки касательных равны.
▲АВО = ▲ СВО → ВА = ВС, ‹ АВО = ‹СВО.
О
А
В
С
О
М
К
О
а
в
90
90
Слайд 17 Определение. Многоугольник называется вписанным в окружность, если все его вершины
Любой
треугольник
можно
вписать в
окружность.
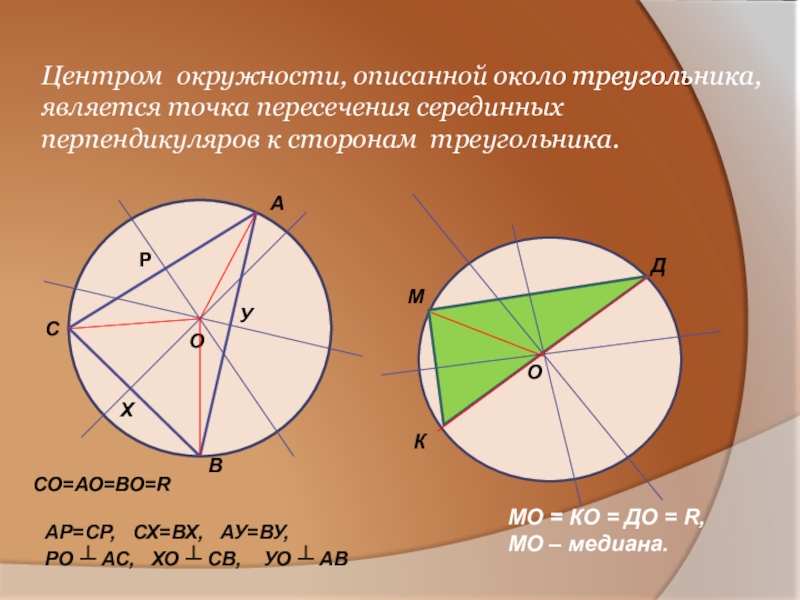
Слайд 18Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к
А
В
С
О
М
К
Д
О
Х
У
Р
АР=СР, СХ=ВХ, АУ=ВУ,
РО ┴ АС, ХО ┴ СВ, УО ┴ АВ
МО = КО = ДО = R,
МО – медиана.
СО=АО=ВО=R
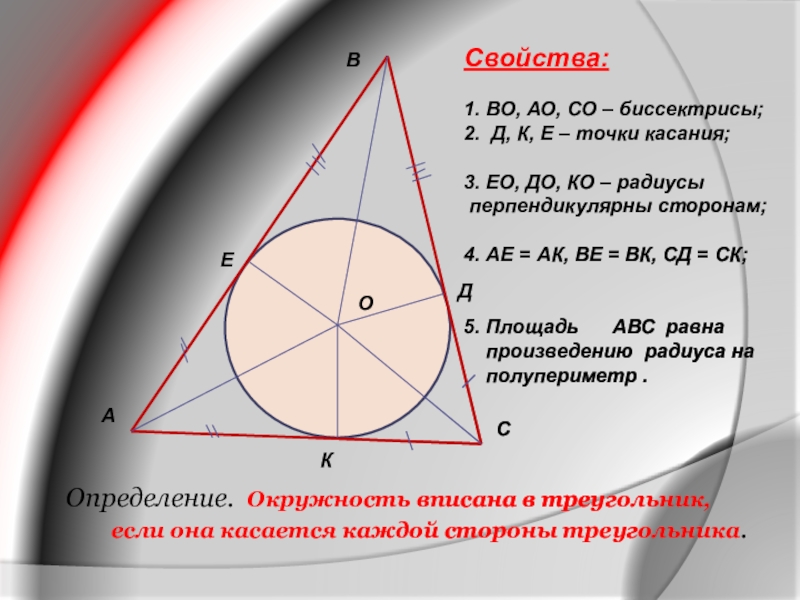
Слайд 19Определение. Окружность вписана в треугольник, если она касается
А
В
С
Д
Е
К
О
Свойства:
1. ВО, АО, СО – биссектрисы;
2. Д, К, Е – точки касания;
3. ЕО, ДО, КО – радиусы
перпендикулярны сторонам;
4. АЕ = АК, ВЕ = ВК, СД = СК;
5. Площадь АВС равна
произведению радиуса на
полупериметр .
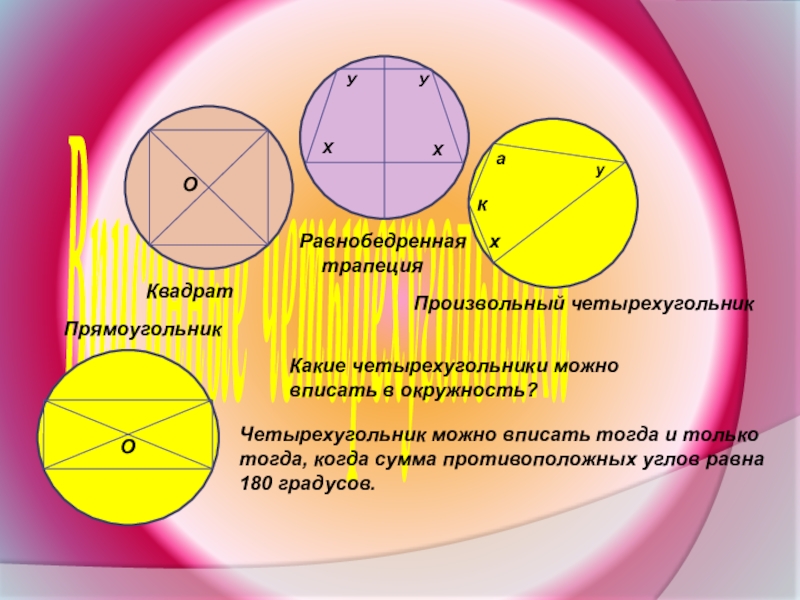
Слайд 21Вписанные четырехугольники
Квадрат
Прямоугольник
Равнобедренная
трапеция
Произвольный четырехугольник
Х
Х
У
У
х
у
к
а
О
О
Какие четырехугольники можно
вписать в окружность?
Четырехугольник можно вписать тогда и только тогда, когда сумма противоположных углов равна 180 градусов.
Слайд 22Окружность, вписанная в четырехугольник
Определение. Окружность называется вписанной в четырехугольник,
Окружность можно вписать в четырехугольник тогда и
только тогда, когда суммы длин противоположных
сторон четырехугольника равны.
А
В
С
Д
АВ +СД = АД +ВС
К
М
Н
Т
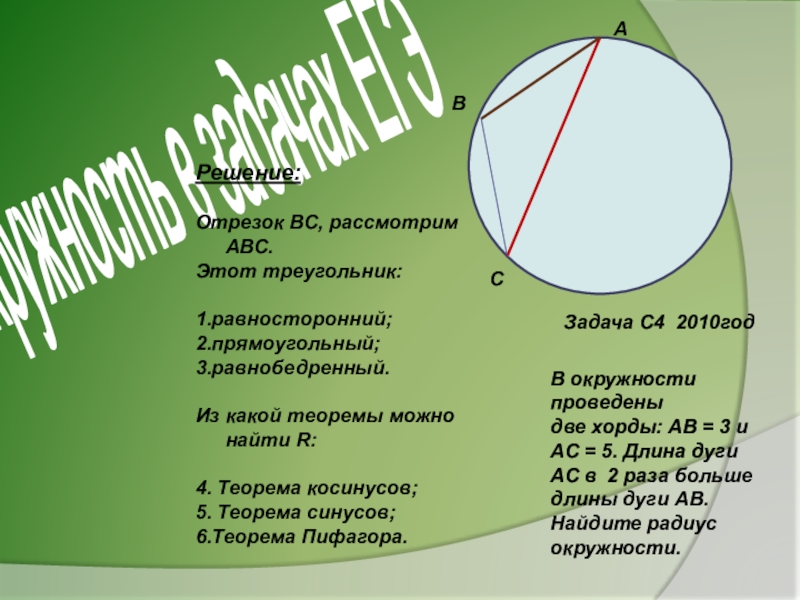
Слайд 23Окружность в задачах ЕГЭ
В окружности
проведены
две хорды: АВ =
АС = 5. Длина дуги
АС в 2 раза больше
длины дуги АВ.
Найдите радиус
окружности.
А
В
С
Задача С4 2010год
Решение:
Отрезок ВС, рассмотрим АВС.
Этот треугольник:
1.равносторонний;
2.прямоугольный;
3.равнобедренный.
Из какой теоремы можно найти R:
4. Теорема косинусов;
5. Теорема синусов;
6.Теорема Пифагора.
Слайд 24Окружность в задачах ЕГЭ
В окружности
проведены
две хорды: АВ =
АС = 5. Длина дуги
АС в 2 раза больше
длины дуги АВ.
Найдите радиус
окружности.
А
В
С
Задача С4 2010год
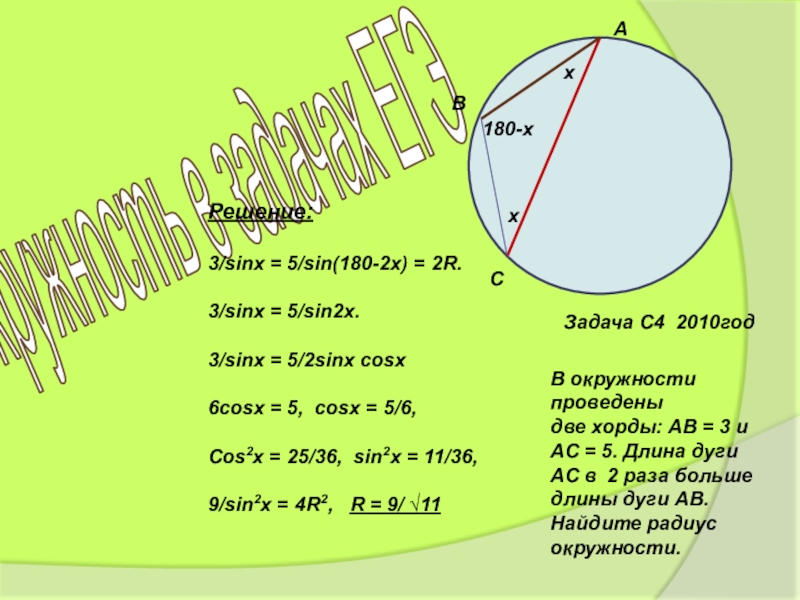
Решение:
3/sinx = 5/sin(180-2x) = 2R.
3/sinx = 5/sin2x.
3/sinx = 5/2sinx cosx
6cosx = 5, cosx = 5/6,
Cos2x = 25/36, sin2x = 11/36,
9/sin2x = 4R2, R = 9/ √11
х
х
180-х
Слайд 25Окружность в задачах ЕГЭ
В окружности
проведены
две хорды: АВ =
АС = 5. Длина дуги
АС в 2 раза больше
длины дуги АВ.
Найдите радиус
окружности.
А
В
С
Задача С4 2010год
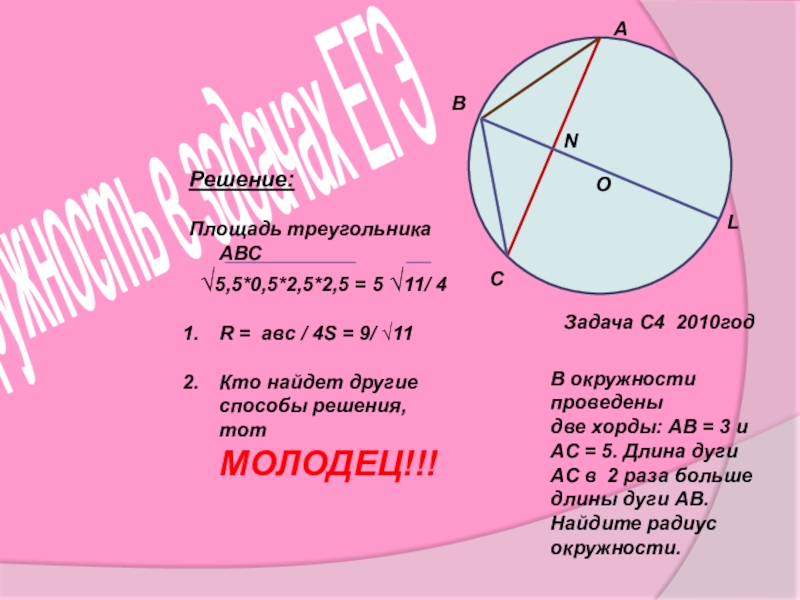
Решение:
Площадь треугольника АВС
√5,5*0,5*2,5*2,5 = 5 √11/ 4
R = авс / 4S = 9/ √11
Кто найдет другие способы решения, тот МОЛОДЕЦ!!!
L
N
O