- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на темуЭто известная и неизвестная теорема Пифагора .
Содержание
- 1. Презентация по математике на темуЭто известная и неизвестная теорема Пифагора .
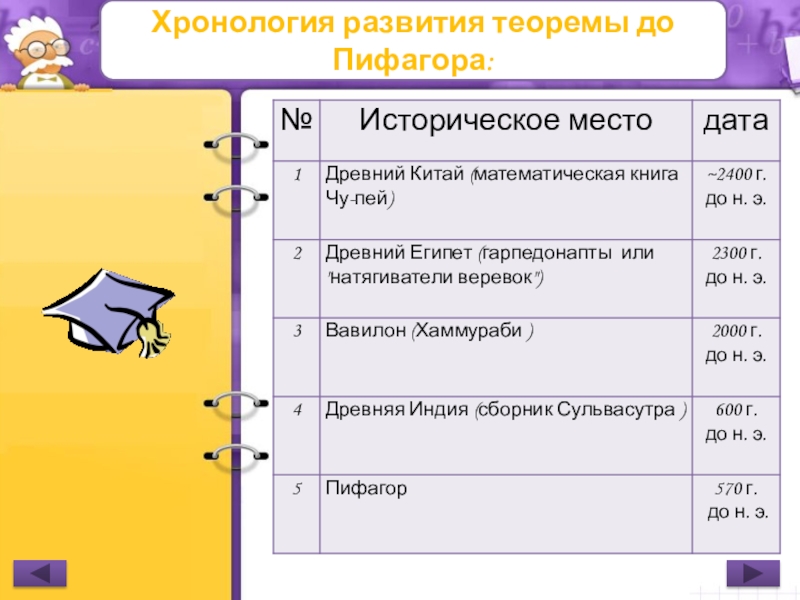
- 2. Хронология развития теоремы до Пифагора:
- 3. Исторический обзор начнём с древнего Китая… Здесь особое
- 4. А далее Древний Египет… Кантор (крупнейший немецкий историк
- 5. Индия… В самом древнем индийском геометрическом сборнике
- 6. Так это вовсе не Пифагор… В настоящее время
- 7. Теорема в книге рекордов Гиннеса Насчитывается более пятисот
- 8. Приведём различные формулировки теоремы Пифагора в переводе
- 9. Латинский перевод: Латинский перевод арабского текста Аннаирици (около
- 10. Немецкий перевод:В Geometria Culmonensis (около 1400 г.)
- 11. Русская версия теоремы В первом русском переводе евклидовых
- 12. Современные формулировки теоремыСуществует три формулировки теоремы Пифагора:1.
- 13. Теорема Пифагора и способы её доказательства Теорема
- 14. Теорема Пифагора и способы её доказательстваЭто прямоугольный треугольник КАТЕТКАТЕТ ГИПОТЕНУЗА
- 15. Теорема Пифагора и способы её доказательства На этом
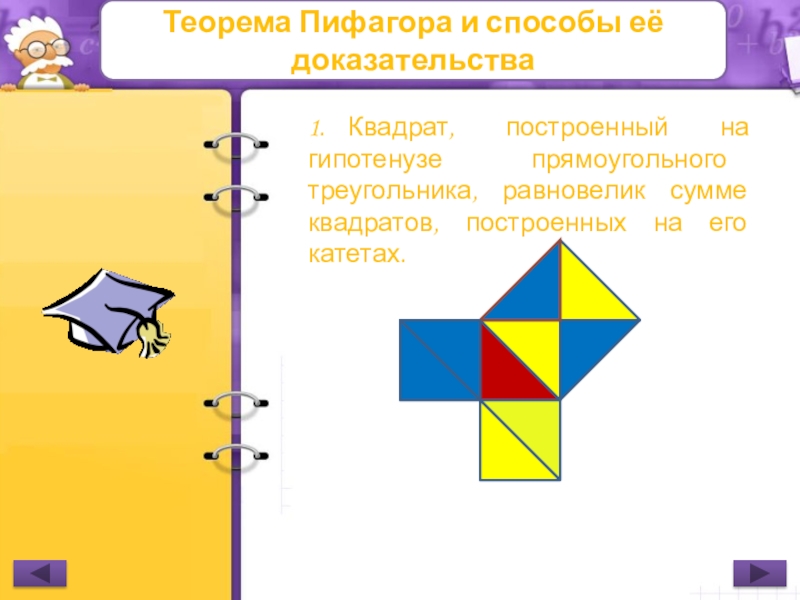
- 16. Теорема Пифагора и способы её доказательства1. Квадрат, построенный
- 17. Теорема Пифагора и способы её доказательстваДоказательство Эйнштейна Дано:
- 18. Теорема Пифагора и способы её доказательстваДоказательство МёльманнаДано:Площадь
- 19. Теорема Пифагора и способы её доказательстваДоказательство МёльманнаДоказательство:Имеем:
- 20. Занимательная задача по теме: "Теорема Пифагора".Древнеиндийская задачаНад
- 21. Занимательная задача по теме: "Теорема Пифагора".Древнеиндийская задачаКакова
- 22. Практическое применение теоремы Пифагора Считать приложения теоремы Пифагора
- 23. Практическое применение теоремы Пифагора В романской архитектуре часто
- 24. Легенды об открытии теоремы Пифагора Открытие теоремы Пифагором
- 25. Уделом истины не может быть забвенье,Как только
- 26. О теореме ПифагораСуть истины вся в том,
- 27. И в заключении… “Геометрия владеет двумя сокровищами: одно
Слайд 3Исторический обзор начнём с древнего Китая…
Здесь особое внимание привлекает математическая книга
“Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4”.
Слайд 4А далее Древний Египет…
Кантор (крупнейший немецкий историк математики) считает, что равенство
По мнению Кантора гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Слайд 5Индия…
В самом древнем индийском геометрическом сборнике «Сульвасутра» («Правила верёвки», 600
Слайд 6Так это вовсе не Пифагор…
В настоящее время известно, что эта теорема
Слайд 7Теорема в книге рекордов Гиннеса
Насчитывается более пятисот доказательств теоремы. Благодаря такому
Слайд 8Приведём различные формулировки теоремы Пифагора в переводе с греческого, латинского и
Греческий перевод:
У Евклида эта теорема гласит (дословный перевод):
"В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол".
Евклид. Гравюра на меди. Примерно XVIII в.
Слайд 9Латинский перевод:
Латинский перевод арабского текста Аннаирици (около 900 г. до н.
"Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол".
Слайд 10Немецкий перевод:
В Geometria Culmonensis (около 1400 г.) теорема читается так: Also,
В переводе это означает:
"Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу".
Слайд 11Русская версия теоремы
В первом русском переводе евклидовых "Начал", сделанном Ф. И.
"В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон,
содержащих прямой угол".
Слайд 12Современные формулировки теоремы
Существует три формулировки теоремы Пифагора:
1. В прямоугольном треугольнике квадрат
2. Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах.
3. Квадрат, построенный на гипотенузе прямоугольного треугольника, равносоставлен с квадратами, построенными на катетах.
Слайд 13Теорема Пифагора и способы её доказательства
Теорема Пифагора – важнейшее утверждение
Слайд 14Теорема Пифагора и способы её доказательства
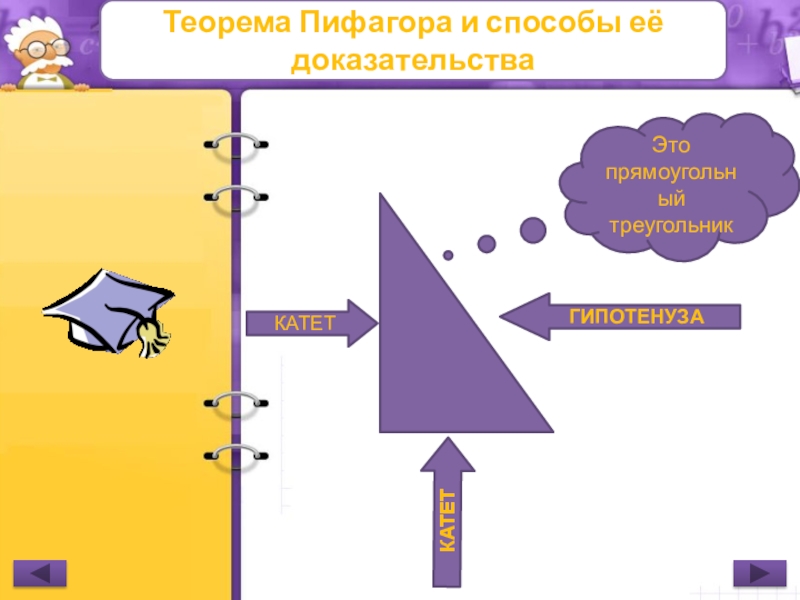
Это прямоугольный треугольник
КАТЕТ
КАТЕТ
ГИПОТЕНУЗА
Слайд 15Теорема Пифагора и способы её доказательства
На этом свойстве прямоугольного треугольника и
Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим —
И таким простым путем
К результату мы придём.
Слайд 16Теорема Пифагора и способы её доказательства
1. Квадрат, построенный на гипотенузе прямоугольного треугольника,
Слайд 17Теорема Пифагора и способы её доказательства
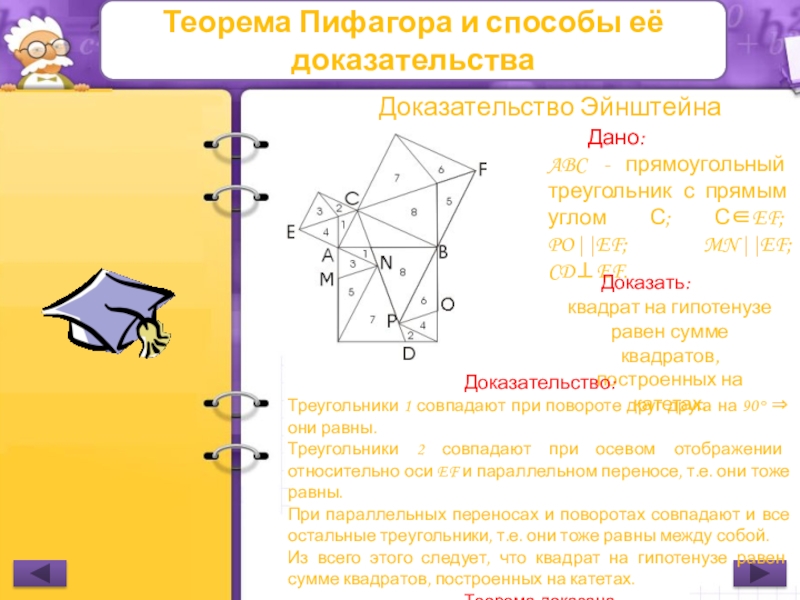
Доказательство Эйнштейна
Дано:
ABC - прямоугольный треугольник
Доказать:
квадрат на гипотенузе равен сумме квадратов, построенных на катетах.
Доказательство:
Треугольники 1 совпадают при повороте друг друга на 90° ⇒ они равны.
Треугольники 2 совпадают при осевом отображении относительно оси EF и параллельном переносе, т.е. они тоже равны.
При параллельных переносах и поворотах совпадают и все остальные треугольники, т.е. они тоже равны между собой.
Из всего этого следует, что квадрат на гипотенузе равен сумме квадратов, построенных на катетах.
Теорема доказана.
Слайд 18Теорема Пифагора и способы её доказательства
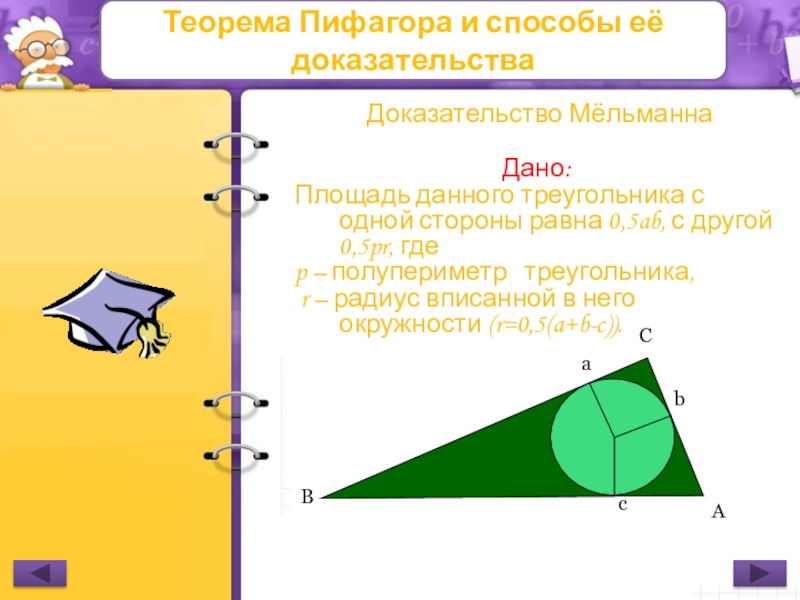
Доказательство Мёльманна
Дано:
Площадь данного треугольника с одной
p – полупериметр треугольника,
r – радиус вписанной в него окружности (r=0,5(a+b-c)).
Слайд 19Теорема Пифагора и способы её доказательства
Доказательство Мёльманна
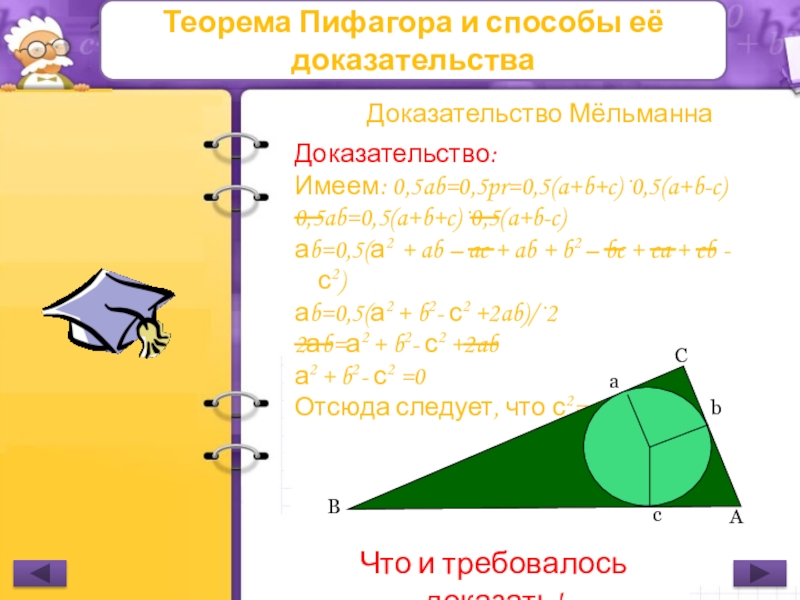
Доказательство:
Имеем: 0,5ab=0,5pr=0,5(a+b+c)·0,5(a+b-c)
0,5ab=0,5(a+b+c)·0,5(a+b-c)
аb=0,5(а2 + ab –
аb=0,5(а2 + b2- с2 +2ab)/·2
2аb=а2 + b2- с2 +2ab
а2 + b2- с2 =0
Отсюда следует, что с2= а2+b2
Что и требовалось доказать!
Слайд 20Занимательная задача по теме: "Теорема Пифагора".
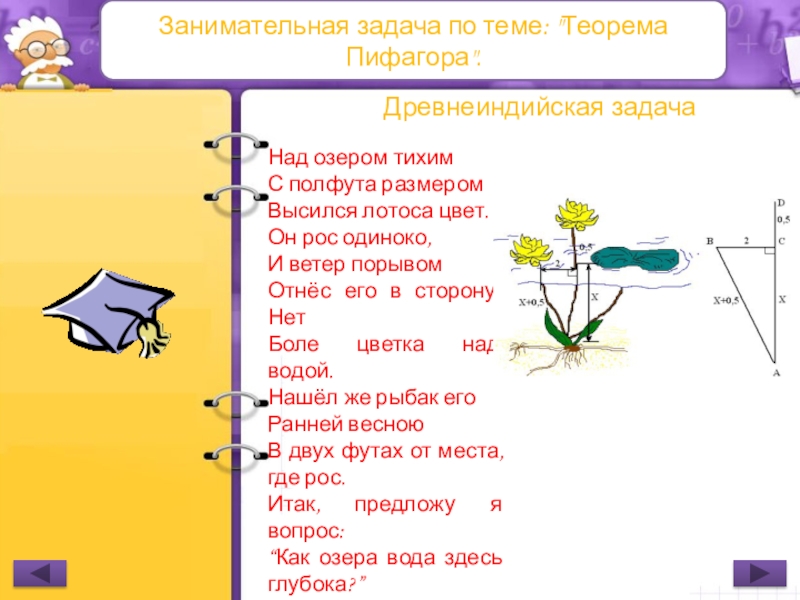
Древнеиндийская задача
Над озером тихим
С полфута размером
Высился
Он рос одиноко,
И ветер порывом
Отнёс его в сторону. Нет
Боле цветка над водой.
Нашёл же рыбак его
Ранней весною
В двух футах от места, где рос.
Итак, предложу я вопрос:
“Как озера вода здесь глубока?”
Слайд 21Занимательная задача по теме: "Теорема Пифагора".
Древнеиндийская задача
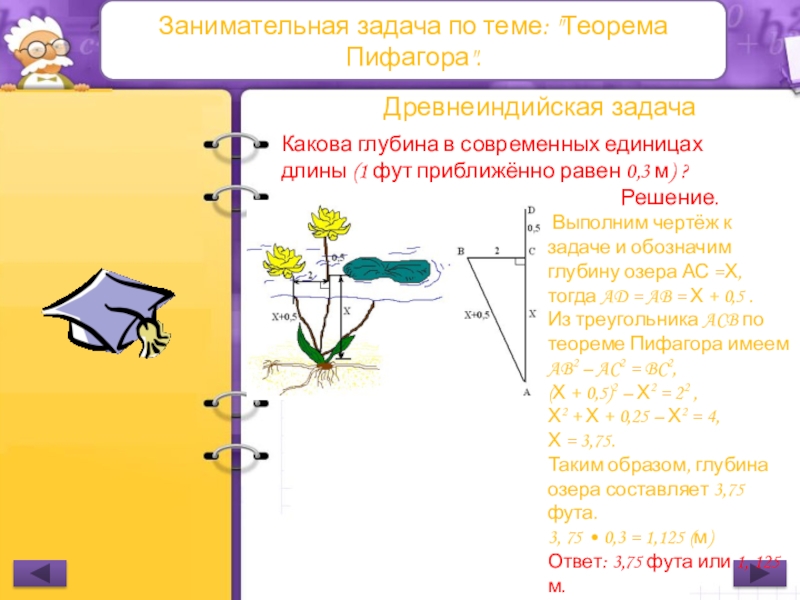
Какова глубина в современных единицах
Решение.
Выполним чертёж к задаче и обозначим глубину озера АС =Х, тогда AD = AB = Х + 0,5 .
Из треугольника ACB по теореме Пифагора имеем AB2 – AC2 = BC2,
(Х + 0,5)2 – Х2 = 22 ,
Х2 + Х + 0,25 – Х2 = 4,
Х = 3,75.
Таким образом, глубина озера составляет 3,75 фута.
3, 75 • 0,3 = 1,125 (м)
Ответ: 3,75 фута или 1, 125 м.
Слайд 22
Практическое применение теоремы Пифагора
Считать приложения теоремы Пифагора только теоретическими - большая
Слайд 23
Практическое применение теоремы Пифагора
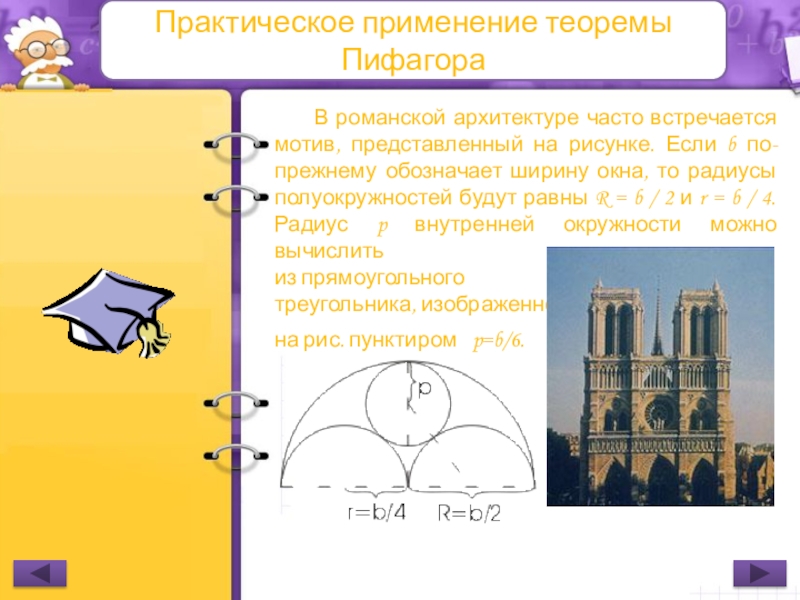
В романской архитектуре часто встречается мотив, представленный на
из прямоугольного
треугольника, изображенного
на рис. пунктиром p=b/6.
Слайд 24
Легенды об открытии теоремы Пифагора
Открытие теоремы Пифагором окружено ореолом красивых легенд.
Слайд 25Уделом истины не может быть забвенье,
Как только мир её увидит взор,
И
Верна теперь, как в день её рожденья.
За светлый луч с небес вознес благодаренье
Мудрец богам не так, как было до тех пор.
Ведь целых сто быков послал он под топор,
Чтоб их сожгли как жертвоприношенье.
Быки с тех пор, как только весть услышат,
Что новой истины уже следы видны,
Отчаянно мычат и ужаса полны:
Им Пифагор навек внушил тревогу.
Не в силах преградить той истине дорогу,
Они, закрыв глаза, дрожат и еле дышат.
О теореме Пифагора
Слайд 26О теореме Пифагора
Суть истины вся в том, что нам она-навечно,
Когда
И теорема Пифагора через столько лет
Для нас, как для него, бесспорна, безупречна.
На радостях богам был Пифагором дан обет:
За то, что мудрости коснулся бесконечной,
Он сто быков заклал, благодаря предвечных;
Моленья и хвалы вознес он жертве вслед.
С тех пор быки, когда, учуют, тужась,
Что к новой истине людей опять подводит след,
Ревут остервенело, так что слушать мочи нет,
Такой в них Пифагор вселил навеки ужас,
Быкам, бессильным новой правде противостоять,
Что остается? - Лишь, глаза закрыв, реветь, дрожать.
Слайд 27И в заключении…
“Геометрия владеет двумя сокровищами: одно из них - это
Иоганн Кеплер