Золотое сечение
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Золотое сечение (9 класс)
Содержание
- 1. Презентация по математике на тему Золотое сечение (9 класс)
- 2. Слайд 2
- 3. ГЕОМЕТРИЯ ВЛАДЕЕТ ДВУМЯ СОКРОВИЩАМИ -ТЕОРЕМОЙ ПИФАГОРА
- 4. Давайте выясним, что общего между древнеегипетскими
- 5. ЦЕЛИ ПРОЕКТА: Познакомить учащихся с
- 6. ПРОБЛЕМА:Существование гармонии в окружающем нас мире. Применение знаний о золотом сечении в исследовании объектов поселка
- 7. ЗАДАЧИ ПРОЕКТА:Подобрать литературу по теме «Золотое сечение»Провести
- 8. В ЧЕМ ЗАКЛЮЧАЕТСЯ ГАРМОНИЯ ОКРУЖАЮЩЕГО НАС МИРА?Золотое сечение
- 9. ИСТОРИЯ «ЗОЛОТОГО СЕЧЕНИЯ»В Древнем Египте существовала «система
- 10. С ИСТОРИЕЙ ЗОЛОТОГО СЕЧЕНИЯ СВЯЗАНО ИМЯ ИТАЛЬЯНСКОГО
- 11. Два главных Платоновых тела, додекаэдр и икосаэдр, основаны на Золотом Сечении.Икосаэдр и додекаэдр
- 12. «ЗОЛОТАЯ ПРОПОРЦИЯ» - ГЛАВНЫЙ ЭСТЕТИЧЕСКИЙ ПРИНЦИП ЭПОХИ
- 13. ВКЛАД КЕПЛЕРА В ТЕОРИЮ ЗОЛОТОГО СЕЧЕНИЯГениальный
- 14. МАТЕМАТИЧЕСКОЕ ПОНИМАНИЕ ГАРМОНИИ«Гармония – соразмерность частей и
- 15. ПОНЯТИЕ «ЗОЛОТОЕ СЕЧЕНИЕ»a : b = b
- 16. Эта пропорция равна: Золотое сечение в процентах
- 17. Дано: отрезок АВ.Построить: золотое сечение отрезка
- 18. АВСЗолотым называется такой равнобедренный треугольник, основание и
- 19. Прямоугольник, стороны которого находятся в золотом отношении,
- 20. ЗАМЕЧАТЕЛЬНЫЙ ПРИМЕР «ЗОЛОТОГО СЕЧЕНИЯ» ПРЕДСТАВЛЯЕТ СОБОЙ ПРАВИЛЬНЫЙ
- 21. ПЕНТАГРАММАЕсли в пентаграмме провести все диагонали, то
- 22. Последовательно отрезая от золотого прямоугольника квадраты и
- 23. ЗОЛОТОЕ СЕЧЕНИЕ В ЖИВОЙ ПРИРОДЕ
- 24. ЗОЛОТОЕ СЕЧЕНИЕ В ПРИРОДЕВсе, что приобретало какую-то
- 25. Слайд 25
- 26. ЗОЛОТОЕ СЕЧЕНИЕ ЛИСТ РОЗЫ Величины
- 27. У многих бабочек соотношение размеров грудной и
- 28. В ящерице с первого взгляда улавливаются приятные
- 29. У многих бабочек узоры на крыльях, соотношение размеров грудной и брюшной части тела соответствуют золотой пропорции
- 30. РОГА И БИВНИ ЖИВОТНЫХ РАЗВИВАЮТСЯ В ФОРМЕ
- 31. Священный холм и храм Божественной Афины, Великолепный
- 32. ЗОЛОТОЕ СЕЧЕНИЕ В АРХИТЕКТУРЕПропорции пирамиды Хеопса,
- 33. ХРАМ ПАРФЕНОН Парфенон имеет 8
- 34. ЗОЛОТОЕ СЕЧЕНИЕ В АРХИТЕКТУРЕ РОССИИ Собор Христа СпасителяСобор Василия Блаженного Проект Смольного собора
- 35. ПО КАКИМ МАТЕМАТИЧЕСКИМ ЗАКОНАМ СОЗДАНЫ МИРОВЫЕ ШЕДЕВРЫ АРХИТЕКТУРЫ И СКУЛЬПТУРЫ?
- 36. ЗОЛОТЫЕ ПРОПОРЦИИ ХРАМА ПОСЕЛКА УСТЬ - ПОРТ
- 37. ЗОЛОТОЕ СЕЧЕНИЕ В ЖИВОПИСИ
- 38. ЗОЛОТОЕ СЕЧЕНИЕ В ЖИВОПИСИ И ФОТОГРАФИИНа живописном
- 39. ЛИЧНОСТЬ ЛЕОНАРДО ДА ВИНЧИ– ОДНА ИЗ ЗАГАДОК
- 40. Портрет Монны Лизы (Джоконды) долгие годы привлекает
- 41. КАРТИНА ШИШКИНА На этой знаменитой
- 42. Васильев «У окна»«Суд Париса» камеяИванов «Явление Христа народу»«Поющий Один» 8 век
- 43. ФОТОГРАФИИ УЧАЩИХСЯ ТКМБОУ «УСТЬ-ПОРТОВСКАЯ СОШ»Наш гербЦветочная пирамидаКрокодил ГенаЗимнее деревоЗимняя сказкаВоробушки
- 44. ЗОЛОТОЕ СЕЧЕНИЕ В СКУЛЬПТУРЕСкульпторы утверждают, что талия
- 45. ВЕЛИКИЙ ДРЕВНЕГРЕЧЕСКИЙ СКУЛЬПТОР ФИДИЙ ЧАСТО ИСПОЛЬЗОВАЛ “ЗОЛОТОЕ
- 46. Шедевром красоты считаетсяАфродита Милосская,созданная Агесандром.Это о ней
- 47. ЗОЛОТОЕ СЕЧЕНИЕ В
- 48. МАТЕМАТИЧЕСКАЯ ЭСТЕТИКА ЦЕЙЗИНГАВ 1855 г. немецкий исследователь
- 49. ИЗМЕРЯЕМ РОСТ И ЛИНИЮ ПОЯСА ИЗМЕРЯЕМ ДЛИНУ ПЛЕЧА, ПРЕДПЛЕЧЬЯ И КИСТИ
- 50. Слайд 50
- 51. РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ УЧАЩИХСЯВывод: пропорции тела мальчиков ближе
- 52. Что такое «золотое сечение»?.. Что это за
- 53. ВЫВОДЫПонятие «золотое сечение» не изучается в школьном
Слайд 1РАБОТУ ВЫПОЛНИЛИ : ОБУЧАЮЩАЯСЯ 9 КЛАССА КУСКОВА ЕЛИЗАВЕТА РУКОВОДИТЕЛЬ ПРОЕКТА: КАРМАНОВА С.С УЧИТЕЛЬ МАТЕМАТИКИ. ТКМБОУ
Слайд 2 НА ЗЕМЛЕ, КАК
Слайд 3ГЕОМЕТРИЯ ВЛАДЕЕТ ДВУМЯ СОКРОВИЩАМИ -ТЕОРЕМОЙ ПИФАГОРА И ЗОЛОТЫМ СЕЧЕНИЕМ. И ЕСЛИ ПЕРВОЕ ИЗ
Слайд 4Давайте выясним,
что общего между древнеегипетскими пирамидами, картиной Леонардо
Слайд 5ЦЕЛИ ПРОЕКТА:
Познакомить учащихся с примерами Золотого сечения в окружающем
Формирование навыков самостоятельной исследовательской деятельности.
Формирование навыков решения ключевой проблемы в процессе сотрудничества и создания продукта, полезного обществу.
Обучение работе с информацией и медиасредствами для расширения кругозора и развития творческих способностей.
Слайд 6ПРОБЛЕМА:
Существование гармонии в окружающем нас мире.
Применение знаний о золотом сечении
Слайд 7ЗАДАЧИ ПРОЕКТА:
Подобрать литературу по теме «Золотое сечение»
Провести исследования по следующим направлениям:
Ознакомиться
Дать формулировку понятия золотого сечения, рассмотреть алгебраический и геометрический смысл
Сформулировать понятие гармонии и математической гармонии
Исследовать пропорции тела человека по Цейзингу
Нахождение пропорции тела человека на примере обучающихся ТКМБОУ «Усть – Портовская СОШ»
Найти подтверждение наличия золотого сечения в природе
Рассмотреть применение золотого сечения в искусстве (скульптура, живопись, фотография)
Ознакомиться с применением золотого сечения в архитектуре
Анализ объектов поселка
Выводы по исследуемой теме
Слайд 9ИСТОРИЯ «ЗОЛОТОГО СЕЧЕНИЯ»
В Древнем Египте существовала «система правил гармонии», основанная на
В Древней Греции Золотое Сечение было своеобразным каноном культуры, который пронизывает все сферы науки и искусства. Красота и гармония стали важнейшими категориями познания.
В толковании древних греков понятие золотого сечения, и понятие гармонии идентичны.
Согласно Пифагору гармония имеет численное выражение, то есть, она связана с концепцией числа.
Евклид излагает теорию Платоновых тел, которая является существенным разделом геометрической теории Золотого Сечения.
Теория гармонии Древних
Слайд 10С ИСТОРИЕЙ ЗОЛОТОГО СЕЧЕНИЯ СВЯЗАНО ИМЯ ИТАЛЬЯНСКОГО МАТЕМАТИКА ЛЕОНАРДО ИЗ ПИЗЫ,
0+1=1, 34: 55=0,618…;
1+1=2, 21:34=0, 617…;
2+1=3, 13:21=0,619…и т.д.
2+3=5 и т.д.,
Каждый член последовательности, начиная с третьего,
равен сумме двух предыдущих, а отношение смежных
чисел ряда приближается к отношению золотого деления.
Все исследователи золотого деления в растительном и в
животном мире, искусстве, неизменно приходили к ряду
Фибоначчи как арифметическому выражению закона
золотого деления.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 …..
Слайд 11Два главных Платоновых тела, додекаэдр и икосаэдр, основаны на Золотом Сечении.
Икосаэдр
Слайд 12«ЗОЛОТАЯ ПРОПОРЦИЯ» - ГЛАВНЫЙ ЭСТЕТИЧЕСКИЙ ПРИНЦИП ЭПОХИ СРЕДНЕВЕКОВЬЯ
Эпоха Возрождения ассоциируется с
Имеется много авторитетных свидетельств о том, что именно Леонардо да Винчи(1452-1519) был одним из первых, кто ввел сам термин «Золотое Сечение».
«Витрувийский человек» - размах вытянутых в сторону рук человека примерно равен его росту, вследствие чего фигура человека вписывается в квадрат и в круг.
Рисунок и текст иногда называют каноническими пропорциями.
Слайд 13ВКЛАД КЕПЛЕРА
В ТЕОРИЮ ЗОЛОТОГО СЕЧЕНИЯ
Гениальный астроном Иоганн Кеплер (1571-1630) был
Считается, что именно Кеплер обратил внимание на ботаническую закономерность филлотаксиса и установил связь между числами Фибоначчи и золотой пропорцией, доказав, что последовательность отношений соседних чисел Фибоначчи:
1/1; 2/1; 3/2; 5/3 ;8/5; 13/8;…в пределе стремится к золотой пропорции
Слайд 14МАТЕМАТИЧЕСКОЕ ПОНИМАНИЕ ГАРМОНИИ
«Гармония – соразмерность частей и целого, слияние различных компонентов
Математическая гармония - это равенство или соразмерность частей с друг другом и части с целым.
Понятие математической гармонии тесно связано с понятиями пропорции и симметрии.
Слайд 15ПОНЯТИЕ «ЗОЛОТОЕ СЕЧЕНИЕ»
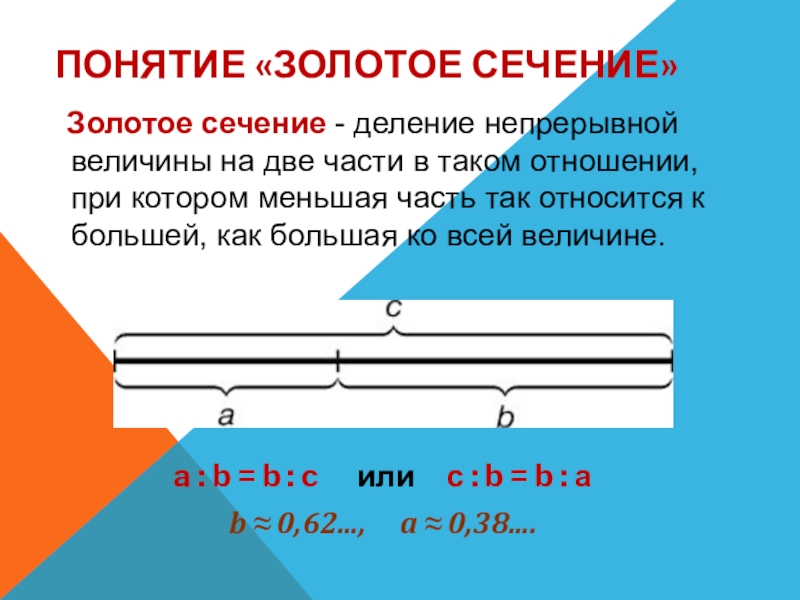
a : b = b : c
b ≈ 0,62..., a ≈ 0,38....
Золотое сечение - деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.
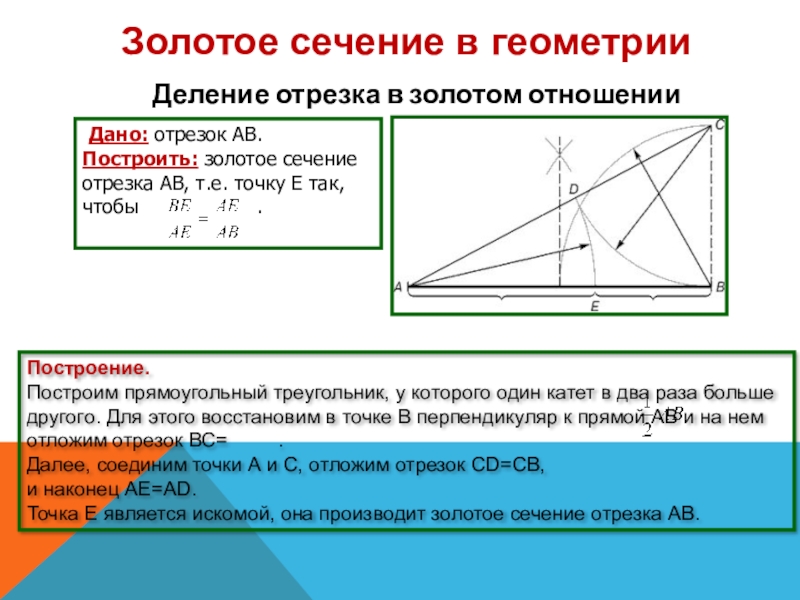
Слайд 17 Дано: отрезок АВ.
Построить: золотое сечение отрезка АВ, т.е. точку Е
Построение.
Построим прямоугольный треугольник, у которого один катет в два раза больше другого. Для этого восстановим в точке В перпендикуляр к прямой АВ и на нем отложим отрезок ВС= .
Далее, соединим точки А и С, отложим отрезок CD=CB,
и наконец AE=AD.
Точка Е является искомой, она производит золотое сечение отрезка АВ.
Деление отрезка в золотом отношении
Золотое сечение в геометрии
Слайд 18А
В
С
Золотым называется такой равнобедренный треугольник, основание и боковая сторона которого находятся
Золотой треугольник
Слайд 19Прямоугольник, стороны которого находятся в золотом отношении, т.е. отношение длины к
Золотой прямоугольник
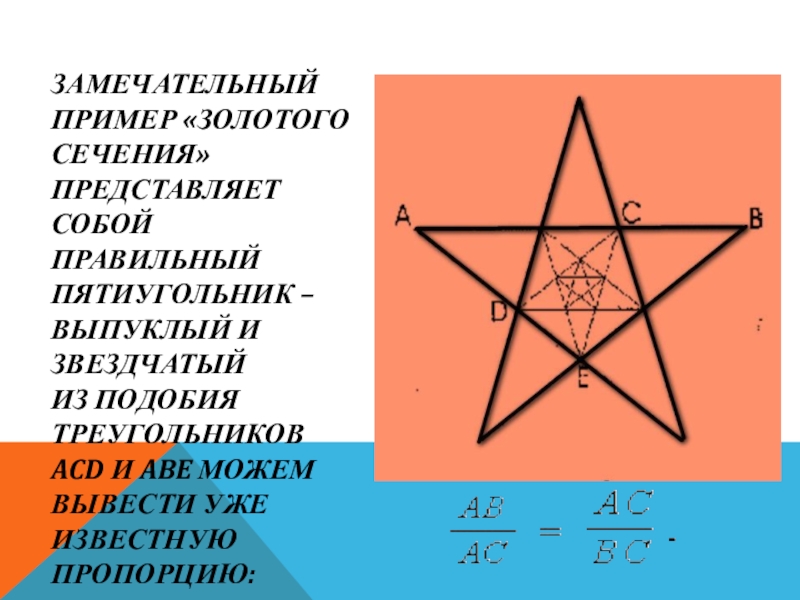
Слайд 20ЗАМЕЧАТЕЛЬНЫЙ ПРИМЕР «ЗОЛОТОГО СЕЧЕНИЯ» ПРЕДСТАВЛЯЕТ СОБОЙ ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК – ВЫПУКЛЫЙ И
Слайд 21ПЕНТАГРАММА
Если в пентаграмме провести все диагонали, то в результате получим пятиугольную
Точки пересечения диагоналей в пентаграмме являются точками золотого сечения диагоналей (отношение синего отрезка к зелёному, красного к синему, зелёного к фиолетовому, равны 1.618). При этом эти точки образуют новую пентаграмму FGHKL и пять правильных треугольников (ADC, ADB,EBD, AEC,EBC)
Здание военного ведомства США имеет форму пентаграммы и получило название «Пентагон», что значит правильный пятиугольник.
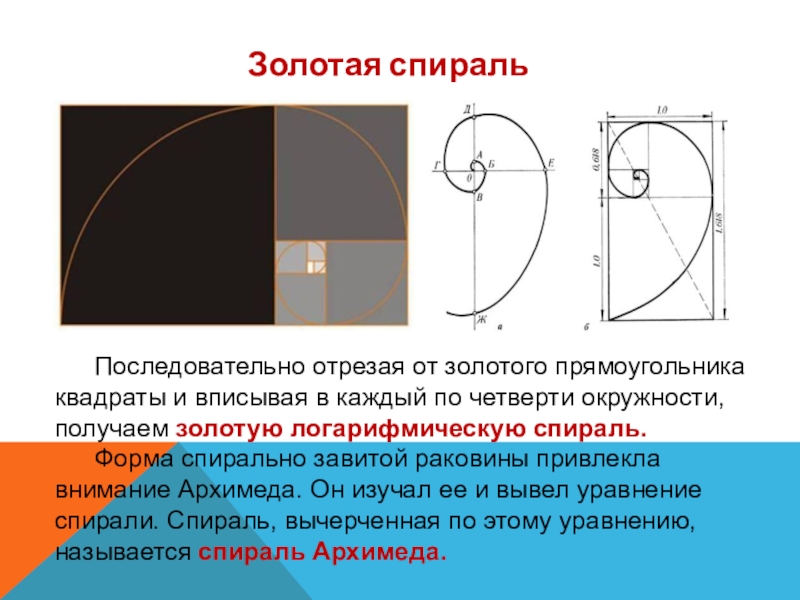
Слайд 22Последовательно отрезая от золотого прямоугольника квадраты и вписывая в каждый по
Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется спираль Архимеда.
Золотая спираль
Слайд 24ЗОЛОТОЕ СЕЧЕНИЕ В ПРИРОДЕ
Все, что приобретало какую-то форму, образовывалось, росло, стремилось
Это стремление находит осуществление в основном в двух вариантах – рост вверх или расстилание по поверхности земли и закручивание по спирали.
Гете называл спираль "кривой жизни". Спираль увидели в расположении семян подсолнечника, в шишках сосны,
ананасах, кактусах и т.д. Паук плетет паутину спиралеобразно.
Слайд 26ЗОЛОТОЕ СЕЧЕНИЕ ЛИСТ РОЗЫ
Величины отростков и лепестков цикория
Между каждыми двумя парами листьев третья расположена в месте золотого сечения
Слайд 27У многих бабочек соотношение размеров грудной и брюшной части тела отвечает
Слайд 28В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции
Можно также заметить золотые пропорции, если внимательно посмотреть на яйцо птицы.
Слайд 29У многих бабочек узоры на крыльях, соотношение размеров грудной и брюшной
Слайд 30РОГА И БИВНИ ЖИВОТНЫХ РАЗВИВАЮТСЯ В ФОРМЕ СПИРАЛИ. БИВНИ СЛОНОВ И
Слайд 31Священный холм и храм
Божественной Афины,
Великолепный Парфенон,
Похоронив забытые руины,
К богам Олимпа устремлен.
Николай
Золотое сечение в архитектуре
Слайд 32ЗОЛОТОЕ СЕЧЕНИЕ
В АРХИТЕКТУРЕ
Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и
Пирамида Хеопса
Слайд 33ХРАМ
ПАРФЕНОН
Парфенон имеет 8 колонн по коротким сторонам и
Слайд 34ЗОЛОТОЕ СЕЧЕНИЕ
В АРХИТЕКТУРЕ РОССИИ
Собор Христа Спасителя
Собор Василия Блаженного
Проект
Слайд 38ЗОЛОТОЕ СЕЧЕНИЕ В ЖИВОПИСИ И ФОТОГРАФИИ
На живописном полотне существуют четыре точки
Зрительные центры расположены на расстоянии 3/8 и 5/8 от краев любой картины и фотографии.
Слайд 39ЛИЧНОСТЬ ЛЕОНАРДО ДА ВИНЧИ– ОДНА ИЗ ЗАГАДОК ИСТОРИИ. ОН СНИСКАЛ СЛАВУ
Слайд 40Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили,
Хитроумная комбинация двух треугольников построена в соответствии с пропорцией золотого сечения.
Слайд 41КАРТИНА ШИШКИНА
На этой знаменитой картине И. И. Шишкина
Ярко освещенная солнцем сосна делит длину картины в отношении золотого сечения.
Слайд 43ФОТОГРАФИИ УЧАЩИХСЯ ТКМБОУ «УСТЬ-ПОРТОВСКАЯ СОШ»
Наш герб
Цветочная пирамида
Крокодил Гена
Зимнее дерево
Зимняя сказка
Воробушки
Слайд 44ЗОЛОТОЕ СЕЧЕНИЕ В СКУЛЬПТУРЕ
Скульпторы утверждают, что талия делит совершенное человеческое тело
Слайд 45ВЕЛИКИЙ ДРЕВНЕГРЕЧЕСКИЙ СКУЛЬПТОР ФИДИЙ ЧАСТО ИСПОЛЬЗОВАЛ “ЗОЛОТОЕ СЕЧЕНИЕ” В СВОИХ ПРОИЗВЕДЕНИЯХ.
Слайд 46Шедевром красоты считается
Афродита Милосская,
созданная Агесандром.
Это о ней написал А.Фет
замечательные строки:
И
Слайд 48МАТЕМАТИЧЕСКАЯ ЭСТЕТИКА
ЦЕЙЗИНГА
В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал
Деление тела точкой пупа – важнейший показатель золотого сечения.
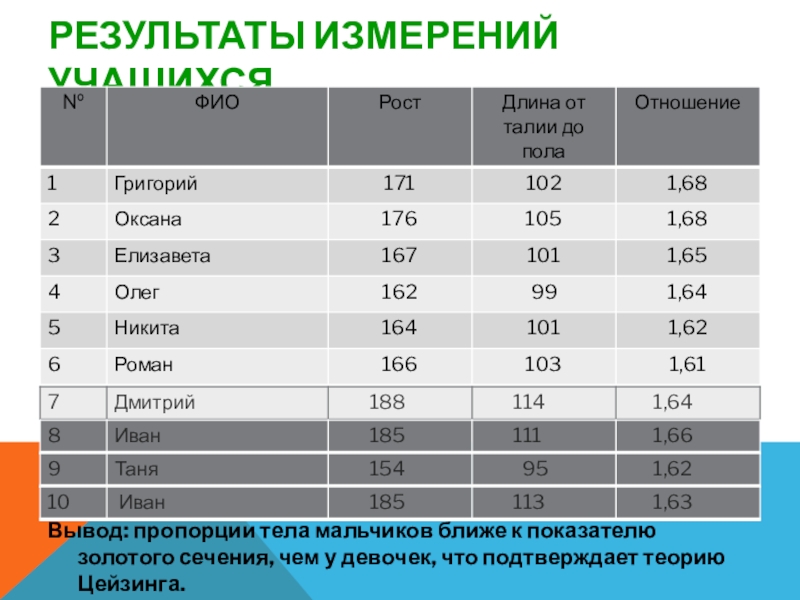
Слайд 51РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ УЧАЩИХСЯ
Вывод: пропорции тела мальчиков ближе к показателю золотого сечения,
Слайд 52Что такое «золотое сечение»?.. Что это за идеальное, божественное сочетание? Может
Анхеля де Куатьэ
Слайд 53ВЫВОДЫ
Понятие «золотое сечение» не изучается в школьном курсе математики, а рассматривается
В данной работе рассмотрены способы нахождения «Золотого сечения», изложены примеры золотой пропорции в природе и теле человека, в архитектуре зданий родного поселка и школы, в расположении зрительных центров на фотографиях, рисунках учащихся.
При общении с проектировщиками и строителями узнали, что при строительстве зданий используются другие формулы. Но мы видим в современной архитектуре гармоничные и красивые сооружения, пропорции которых совпадают с коэффициентом золотого сечения.
В своей работе хотели продемонстрировать красоту и широту «Золотого сечения» в реальной жизни. Проведенные исследования доказали, что многое в окружающей природе подчиняется правилу золотого сечения.
СПАСИБО ЗА ВНИМАНИЕ !