пересекаться – иметь две общие точки.
Могут касаться – иметь одну общую точку.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Взаимное расположение двух окружностей
Содержание
- 1. Презентация по математике на тему Взаимное расположение двух окружностей
- 2. Пересечение двух окружностей Первая окружность: О₁ -
- 3. Окружности не пересекаются Первая окружность: О₁ -
- 4. Окружности касаются внешним образом Первая окружность: О₁
- 5. Окружности касаются внутренним образом Первая окружность: О₁
- 6. Задачи №1. Радиусы окружностей равны 10 см
- 7. Задачи №3. Две окружности касаются внешним образом.
Пересечение двух окружностей Первая окружность: О₁ - центр, r₁ - радиус Вторая окружность: О₂ - центр, r₂ - радиус
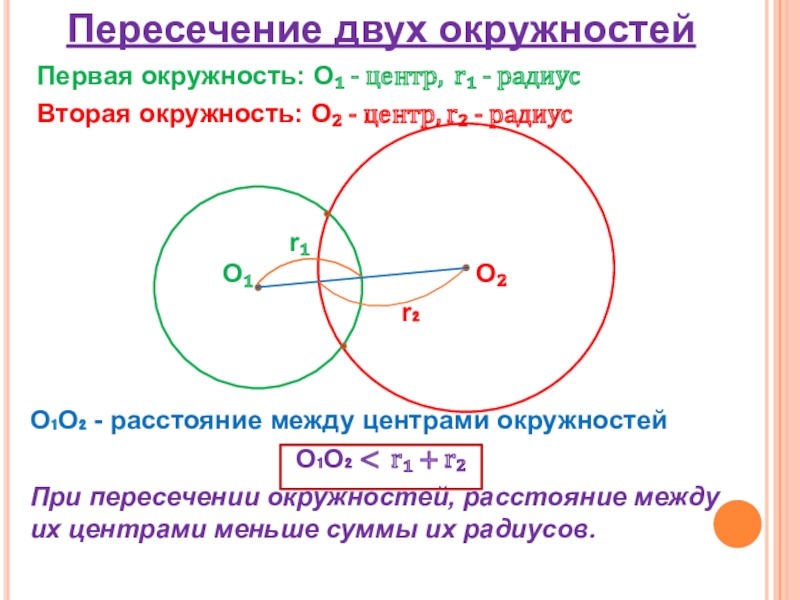
Слайд 2Пересечение двух окружностей
Первая окружность: О₁ - центр, r₁ - радиус
Вторая окружность: О₂ - центр, r₂ - радиус
r₁
O₁ О₂
r₂
О₁О₂ - расстояние между центрами окружностей
О₁О₂ < r₁ + r₂
При пересечении окружностей, расстояние между их центрами меньше суммы их радиусов.
r₁
O₁ О₂
r₂
О₁О₂ - расстояние между центрами окружностей
О₁О₂ < r₁ + r₂
При пересечении окружностей, расстояние между их центрами меньше суммы их радиусов.
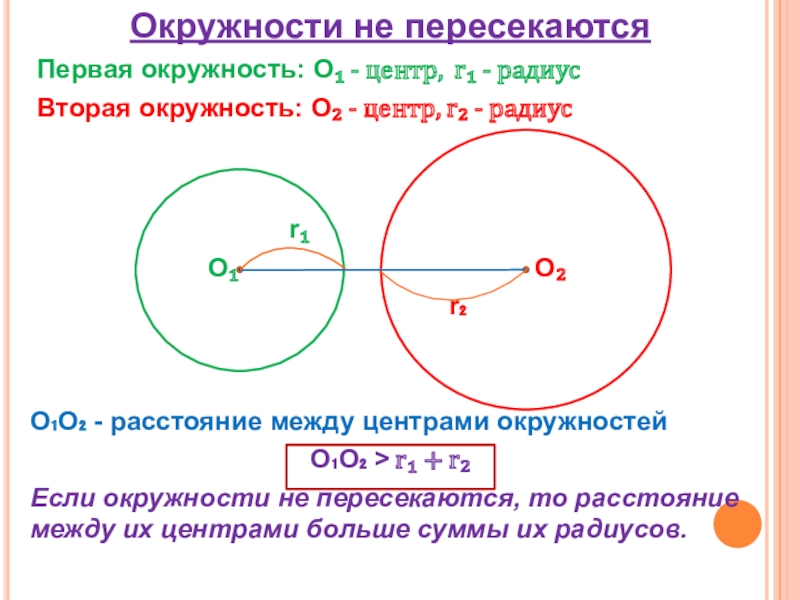
Слайд 3Окружности не пересекаются
Первая окружность: О₁ - центр, r₁ - радиус
Вторая окружность: О₂ - центр, r₂ - радиус
r₁
O₁ О₂
r₂
О₁О₂ - расстояние между центрами окружностей
О₁О₂ > r₁ + r₂
Если окружности не пересекаются, то расстояние между их центрами больше суммы их радиусов.
r₁
O₁ О₂
r₂
О₁О₂ - расстояние между центрами окружностей
О₁О₂ > r₁ + r₂
Если окружности не пересекаются, то расстояние между их центрами больше суммы их радиусов.
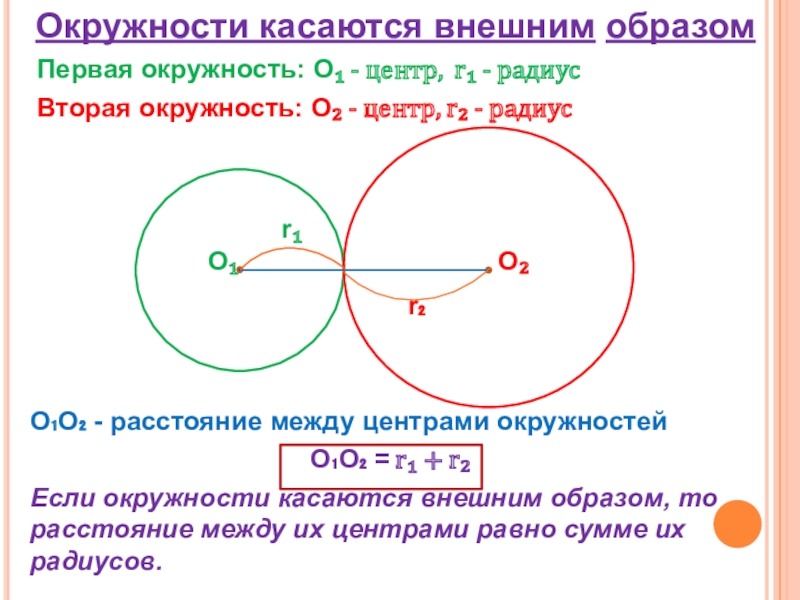
Слайд 4Окружности касаются внешним образом
Первая окружность: О₁ - центр, r₁ -
радиус
Вторая окружность: О₂ - центр, r₂ - радиус
r₁
O₁ О₂
r₂
О₁О₂ - расстояние между центрами окружностей
О₁О₂ = r₁ + r₂
Если окружности касаются внешним образом, то расстояние между их центрами равно сумме их радиусов.
Вторая окружность: О₂ - центр, r₂ - радиус
r₁
O₁ О₂
r₂
О₁О₂ - расстояние между центрами окружностей
О₁О₂ = r₁ + r₂
Если окружности касаются внешним образом, то расстояние между их центрами равно сумме их радиусов.
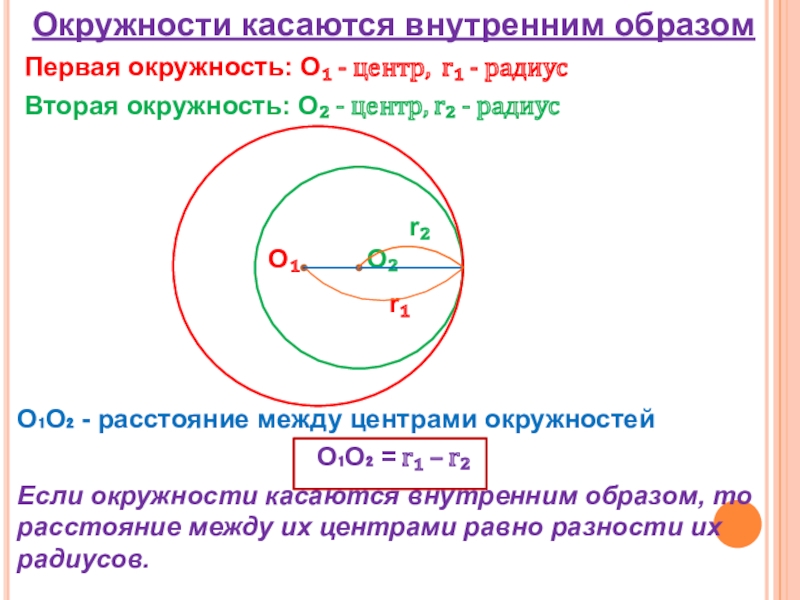
Слайд 5Окружности касаются внутренним образом
Первая окружность: О₁ - центр, r₁ -
радиус
Вторая окружность: О₂ - центр, r₂ - радиус
r₂
O₁ О₂
r₁
О₁О₂ - расстояние между центрами окружностей
О₁О₂ = r₁ – r₂
Если окружности касаются внутренним образом, то расстояние между их центрами равно разности их радиусов.
Вторая окружность: О₂ - центр, r₂ - радиус
r₂
O₁ О₂
r₁
О₁О₂ - расстояние между центрами окружностей
О₁О₂ = r₁ – r₂
Если окружности касаются внутренним образом, то расстояние между их центрами равно разности их радиусов.
Слайд 6Задачи
№1. Радиусы окружностей равны 10 см и 24 см, а
расстояние между центрами равно 30 см. Сколько точек пересечения имеют окружности?
Решение: r₁=10 cм, r₂=24 cм, О₁О₂=30 см
получаем r₁+ r₂=10см + 24 cм=34 см,
видим, что О₁О₂ < r₁+ r₂, значит окружности
пересекаются в двух точках (смотри слайд 2)
№2. Радиусы окружностей равны 23 см и 15 см, а расстояние между центрами равно 60 см. Сколько точек пересечения имеют окружности?
Решение: r₁=23 cм, r₂=15 cм, О₁О₂=60 см
получаем r₁+ r₂=23см + 15 cм=38 см,
видим, что О₁О₂ > r₁+ r₂, значит окружности
не пересекаются (смотри слайд 3)
Решение: r₁=10 cм, r₂=24 cм, О₁О₂=30 см
получаем r₁+ r₂=10см + 24 cм=34 см,
видим, что О₁О₂ < r₁+ r₂, значит окружности
пересекаются в двух точках (смотри слайд 2)
№2. Радиусы окружностей равны 23 см и 15 см, а расстояние между центрами равно 60 см. Сколько точек пересечения имеют окружности?
Решение: r₁=23 cм, r₂=15 cм, О₁О₂=60 см
получаем r₁+ r₂=23см + 15 cм=38 см,
видим, что О₁О₂ > r₁+ r₂, значит окружности
не пересекаются (смотри слайд 3)
Слайд 7Задачи
№3. Две окружности касаются внешним образом.
Радиус первой окружности 18
см, а второй 27 см.
Найдите расстояние между центрами этих окружностей.
Решение: r₁=18 cм, r₂=27 cм, О₁О₂= ?
окружности касаются внешним образом,
значит : О₁О₂ = r₁+ r₂
получаем О₁О₂ = 18 см + 27 см=45 см (смотри слайд 4)
№4. Две окружности касаются внутренним образом.
Радиус первой окружности 49 см, а второй 12 см.
Найдите расстояние между центрами этих окружностей.
Решение: r₁=49 cм, r₂=12 cм, О₁О₂= ?
окружности касаются внутренним образом,
значит : О₁О₂ = r₁– r₂
получаем О₁О₂ = 49 см – 12 см=37 см (смотри слайд 5)
Найдите расстояние между центрами этих окружностей.
Решение: r₁=18 cм, r₂=27 cм, О₁О₂= ?
окружности касаются внешним образом,
значит : О₁О₂ = r₁+ r₂
получаем О₁О₂ = 18 см + 27 см=45 см (смотри слайд 4)
№4. Две окружности касаются внутренним образом.
Радиус первой окружности 49 см, а второй 12 см.
Найдите расстояние между центрами этих окружностей.
Решение: r₁=49 cм, r₂=12 cм, О₁О₂= ?
окружности касаются внутренним образом,
значит : О₁О₂ = r₁– r₂
получаем О₁О₂ = 49 см – 12 см=37 см (смотри слайд 5)