Горно-Алтайска.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
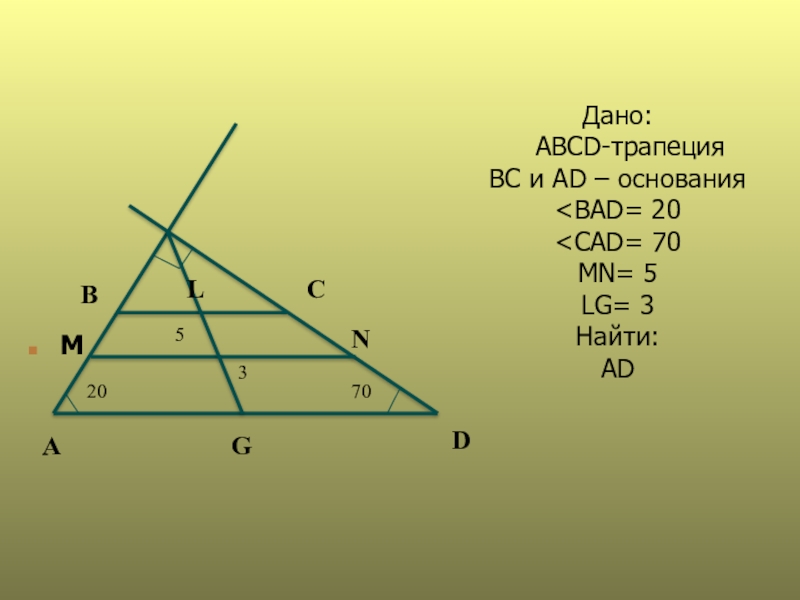
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Вторая средняя линяя трапеции (9 класс)
Содержание
- 1. Презентация по математике на тему Вторая средняя линяя трапеции (9 класс)
- 2. ВТОРАЯ СРЕДНЯЯ ЛИНИЯТРАПЕЦИИ?????
- 3. Задачи: -Собрать информацию о второй средней линии
- 4. Слайд 4
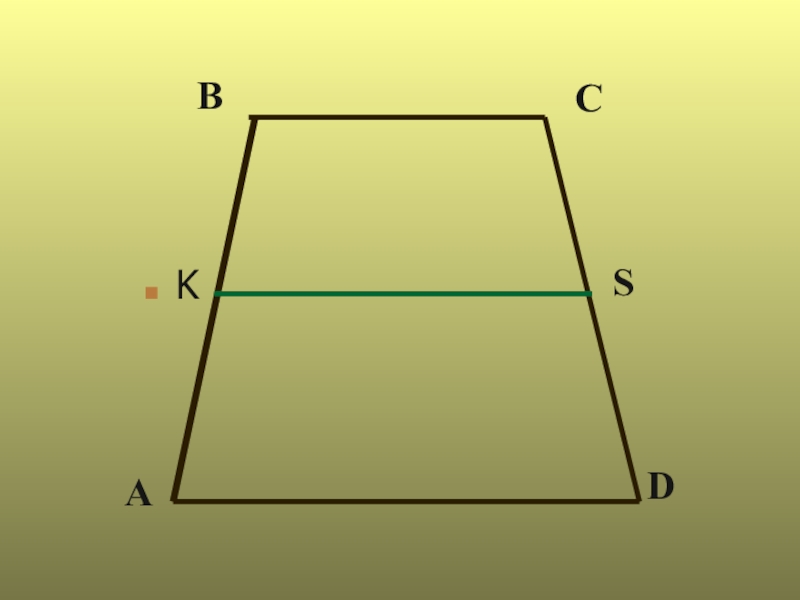
- 5. AKBDSC
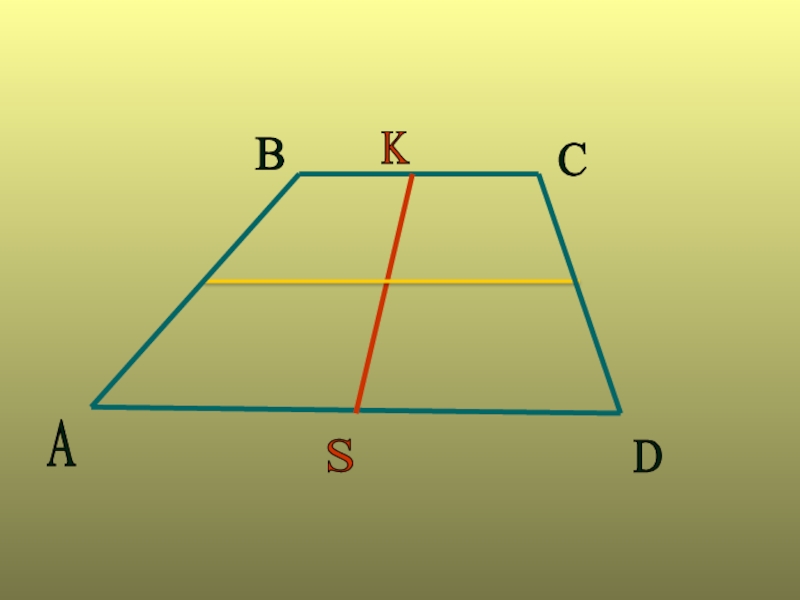
- 6. B K C A S D
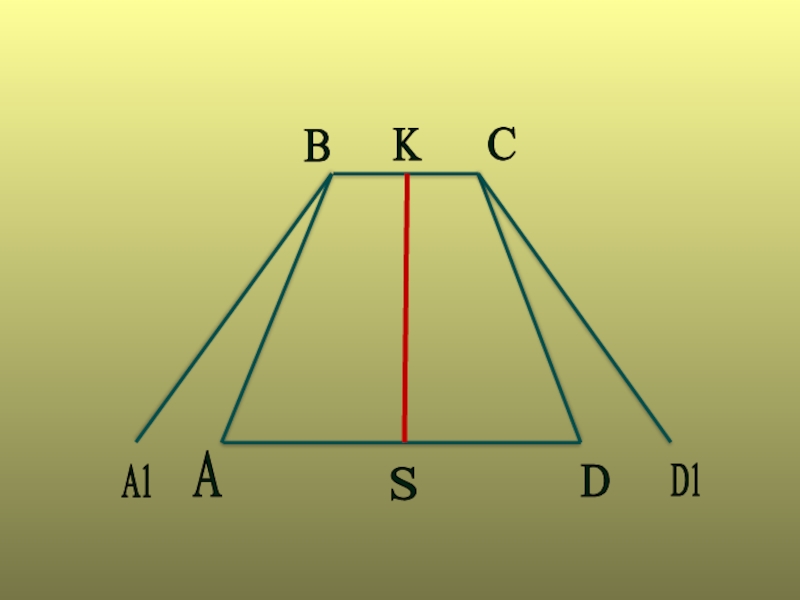
- 7. B K C D S A A1 D1
- 8. B K C D S A A1
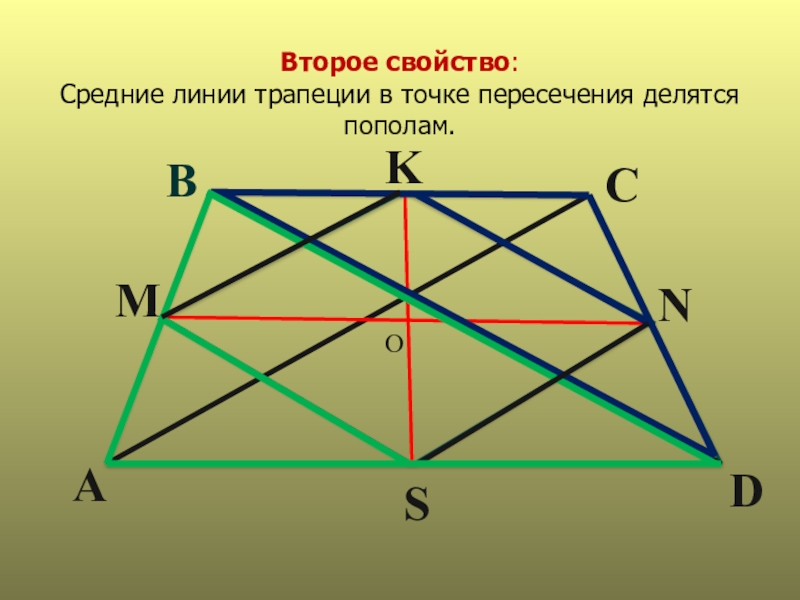
- 9. Второе свойство: Средние линии трапеции в точке пересечения делятся пополам. АBMKCNDSO
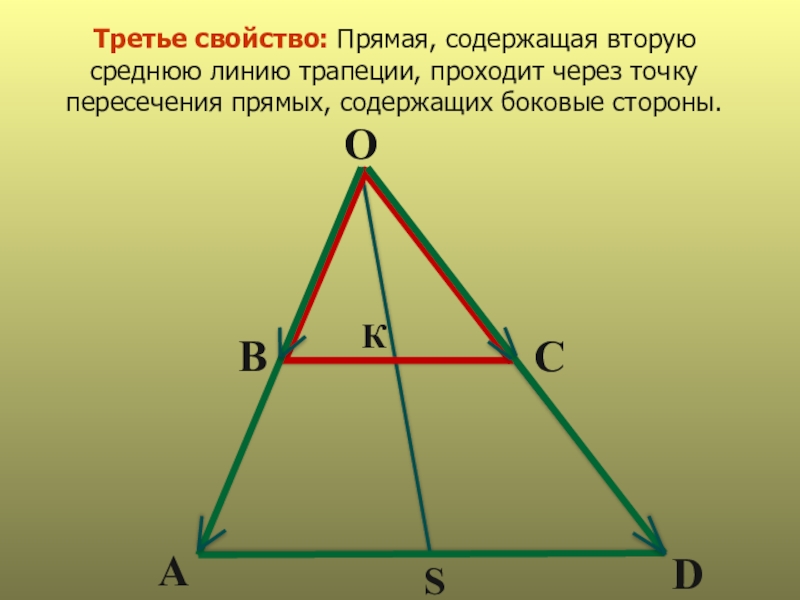
- 10. Третье свойство: Прямая, содержащая вторую среднюю линию трапеции, проходит через точку пересечения прямых, содержащих боковые стороны.ABOCDSК
- 11. Верно и обратное утверждение: если прямая проходит
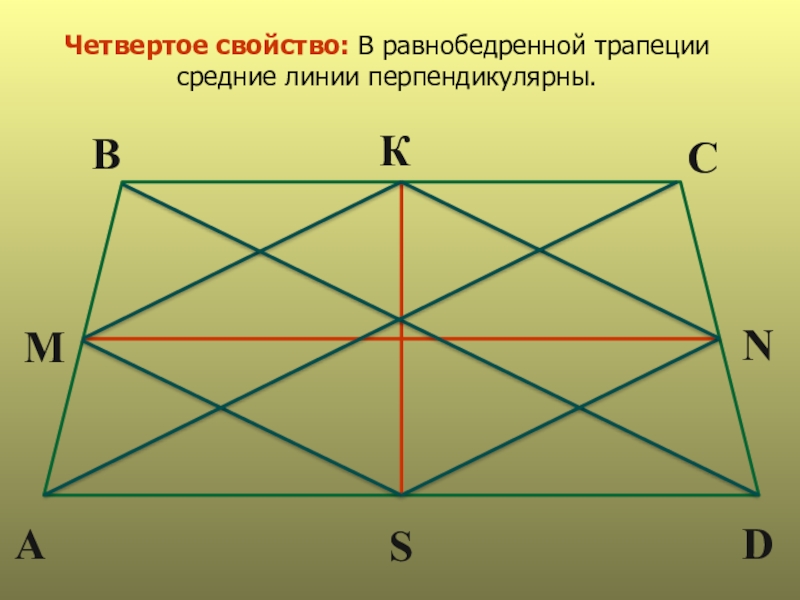
- 12. Четвертое свойство: В равнобедренной трапеции средние линии перпендикулярны.ВКСМАSDN
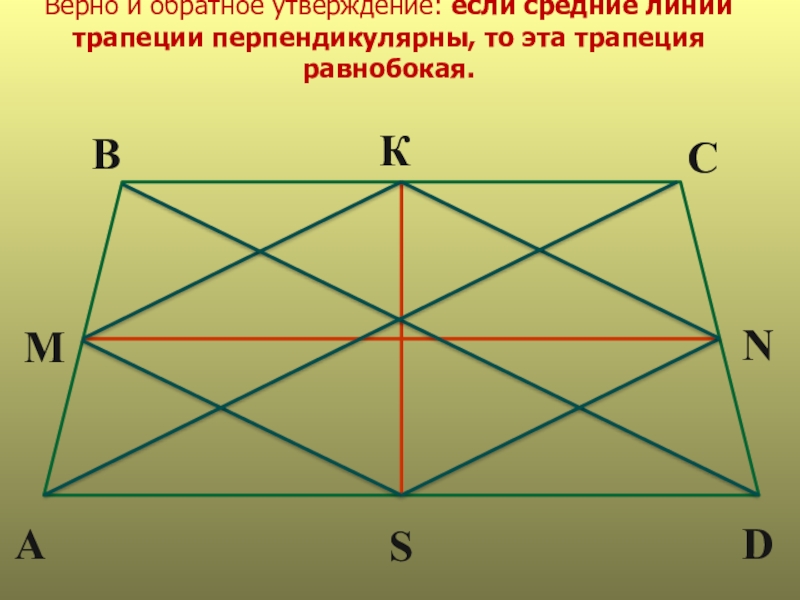
- 13. Верно и обратное утверждение: если средние линии трапеции перпендикулярны, то эта трапеция равнобокая. ВКСМАSDN
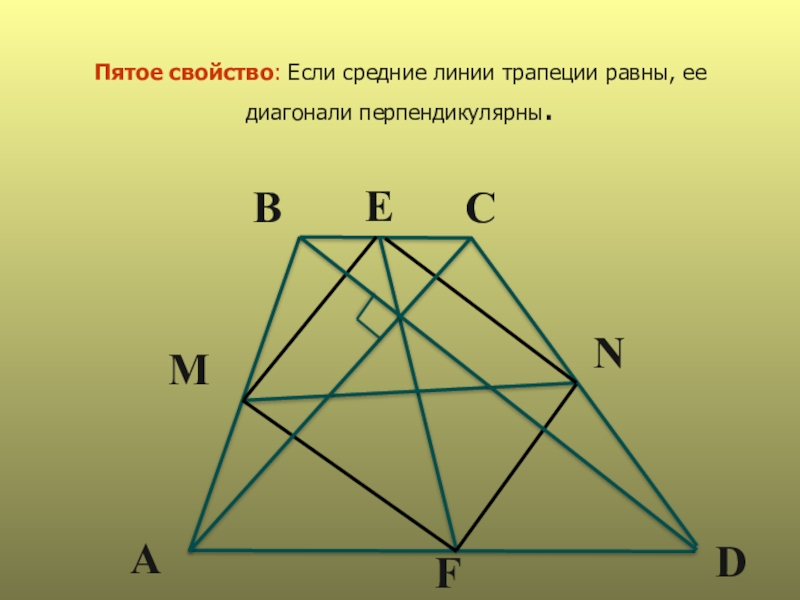
- 14. Пятое свойство: Если средние линии трапеции равны, ее диагонали перпендикулярны.АМВЕFCND
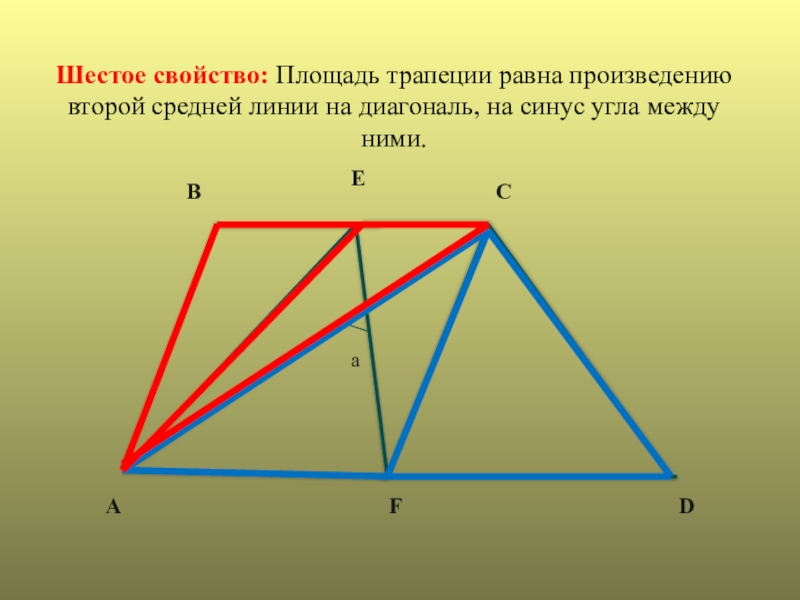
- 15. AEBDFCaШестое свойство: Площадь трапеции равна произведениювторой средней линии на диагональ, на синус угла междуними.
- 16. Задача 2 Дано: ABCD- трапеция
- 17. ABOCDSКЗадача 3 Как с помощью одной линейки
- 18. Задача 4.(№820) Докажите, что прямая, проходящая через
- 19. Дано: ABCD-трапеция ВC и AD – основания
- 20. Заключение В результате проделанной работы я узнала, что
- 21. Слайд 21
ВТОРАЯ СРЕДНЯЯ ЛИНИЯТРАПЕЦИИ?????
Слайд 3
Задачи:
-Собрать информацию о второй средней линии трапеции.
-Изучить свойства второй средней
линии трапеции.
-Решить задачи, имеющиеся в литературе.
-Решить задачи, имеющиеся в литературе.
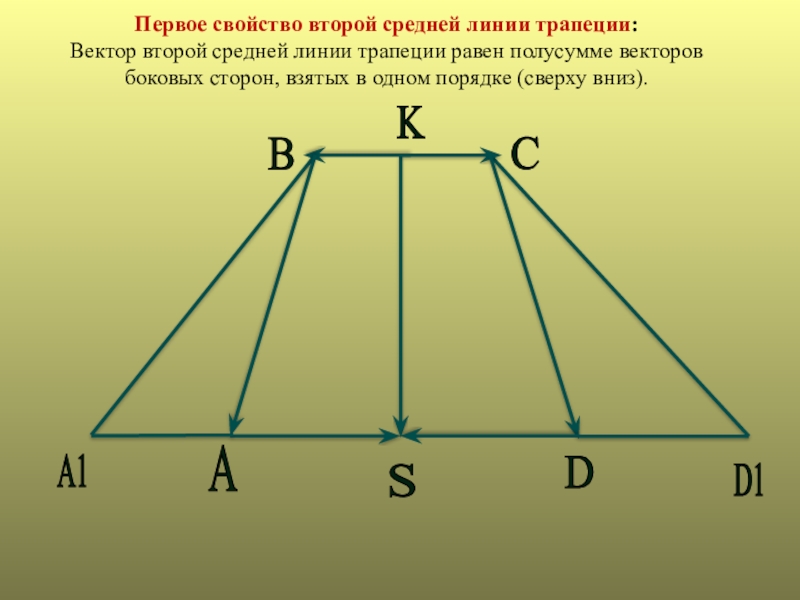
Слайд 8B
K
C
D
S
A
A1
D1
Первое свойство второй
средней линии трапеции:
Вектор второй средней линии трапеции равен полусумме векторов
боковых сторон, взятых в одном порядке (сверху вниз).
Вектор второй средней линии трапеции равен полусумме векторов
боковых сторон, взятых в одном порядке (сверху вниз).
Слайд 10Третье свойство: Прямая, содержащая вторую среднюю линию трапеции, проходит через точку
пересечения прямых, содержащих боковые стороны.
A
B
O
C
D
S
К
Слайд 11Верно и обратное утверждение: если прямая проходит через точку пересечения прямых,
содержащих боковые стороны и середину одного из оснований, то она проходит и через середину другого основания (является второй средней линией трапеции).
Слайд 13Верно и обратное утверждение: если средние линии трапеции перпендикулярны, то эта
трапеция равнобокая.
В
К
С
М
А
S
D
N
Слайд 15A
E
B
D
F
C
a
Шестое свойство: Площадь трапеции равна произведению
второй средней линии на диагональ, на
синус угла между
ними.
ними.
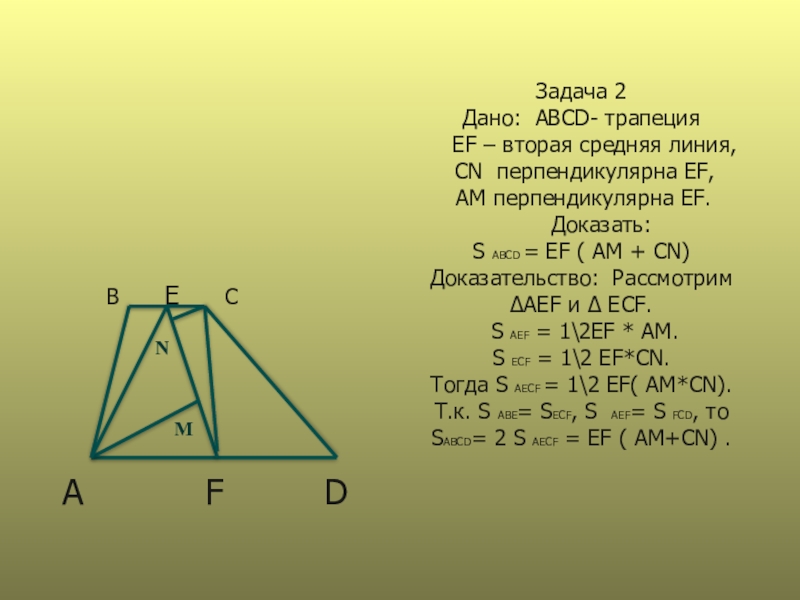
Слайд 16Задача 2 Дано: ABCD- трапеция EF –
вторая средняя линия,
СN перпендикулярна EF,
AM перпендикулярна EF.
Доказать:
S ABCD = EF ( AM + CN)
Доказательство: Рассмотрим
∆AEF и ∆ ECF.
S AEF = 1\2EF * AM.
S ECF = 1\2 EF*CN.
Тогда S AECF = 1\2 EF( AM*CN).
Т.к. S ABE= SECF, S AEF= S FCD, то
SABCD= 2 S AECF = EF ( AM+CN) .
B Е C
A F D
M
N
Слайд 17A
B
O
C
D
S
К
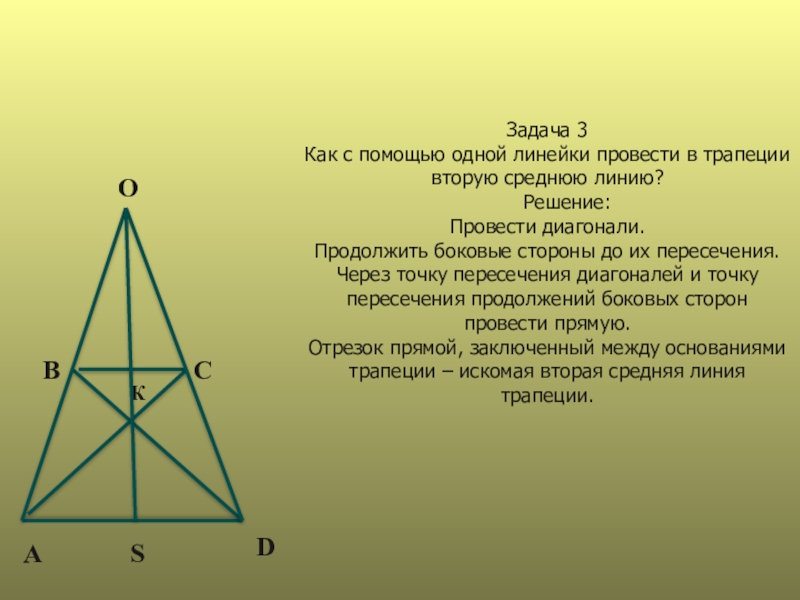
Задача 3
Как с помощью одной линейки провести в трапеции вторую среднюю
линию?
Решение:
Провести диагонали.
Продолжить боковые стороны до их пересечения.
Через точку пересечения диагоналей и точку пересечения продолжений боковых сторон провести прямую.
Отрезок прямой, заключенный между основаниями трапеции – искомая вторая средняя линия трапеции.
Слайд 18Задача 4.
(№820) Докажите, что прямая, проходящая через середины оснований равнобедренной трапеции,
перпендикулярна к основаниям.
Решение: см. доказательство свойства 4.
Решение: см. доказательство свойства 4.
Слайд 20
Заключение
В результате проделанной работы я узнала, что такое вторая средняя линия
трапеции, какими свойствами она обладает; разобрала решение задач, связанных с этой линией.
Я выяснила, что вторая средняя линия трапеции используется в решении задач мало, видимо, поэтому она не проходится в школе. Но я не жалею, что потратила время на изучение этой темы, т.к. узнала много нового о трапеции.
Я выяснила, что вторая средняя линия трапеции используется в решении задач мало, видимо, поэтому она не проходится в школе. Но я не жалею, что потратила время на изучение этой темы, т.к. узнала много нового о трапеции.
Слайд 21
Литература
Л. С. Атанасян и др. «Геометрия 7-9» Учебник для образовательных учреждений/- М., Просвещение, 2006
Википедия.- ru.wikipedia.org/wiki/средняя линия
И. А. Кушнир «Вторая средняя линия трапеции», журнал «Математика в школе» №2, 1993.
В. Б. Лидский, Л. В. Овсянников, А. Н. Тулайков, М. И. Шабунин «Задачи по элементарной математике» - М., Физматгиз, 1960.
Научный форум dxdy. – dxdy.ru/topic20315.html
В. В. Прасолов «Задачи по планиметрии» -М.: Наука, 1986.
И. Х. Сивашинский «Задачник по элементарной математике», - М., Наука, 1966.
Фестиваль идей – portfolio.1september.ru/work
Л. С. Атанасян и др. «Геометрия 7-9» Учебник для образовательных учреждений/- М., Просвещение, 2006
Википедия.- ru.wikipedia.org/wiki/средняя линия
И. А. Кушнир «Вторая средняя линия трапеции», журнал «Математика в школе» №2, 1993.
В. Б. Лидский, Л. В. Овсянников, А. Н. Тулайков, М. И. Шабунин «Задачи по элементарной математике» - М., Физматгиз, 1960.
Научный форум dxdy. – dxdy.ru/topic20315.html
В. В. Прасолов «Задачи по планиметрии» -М.: Наука, 1986.
И. Х. Сивашинский «Задачник по элементарной математике», - М., Наука, 1966.
Фестиваль идей – portfolio.1september.ru/work