- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Виды математических понятий
Содержание
- 1. Презентация по математике на тему Виды математических понятий
- 2. Одной из задач развития математического
- 3. Объем понятия Объем понятия - это
- 4. Объем понятия
- 5. Содержание понятия - та система существенных свойств
- 6. Содержание понятияПараллелограмм:- выпуклый четырехугольник;- стороны попарно параллельны
- 7. Виды понятий Конъюнктивные понятия.
- 8. Правило заключения о принадлежности объекта к понятию
- 9. Логическое правило действия (написано на учебной
- 10. Логическое правило действия (написано на учебной карточке)
- 11. Правило заключения о принадлежности объекта к
- 12. Логическое правило действия (написано на учебной карточке)
- 13. Примеры понятийС дизъюнктивной структурой признаковНеправильная дробь:Числитель больше
- 14. Абсолютные понятия Абсолютные понятия объединяют предметы
- 15. Относительные понятия Относительные понятия объединяют объекты
- 16. Относительные понятия Число зависит и от
- 17. По степени обобщенности Родовое понятие (более
- 18. Примеры Четырехугольники — родовое понятие для параллелограмма;
- 19. Виды действий, используемых при формировании понятий.
- 20. Действие подведения под понятие-указание системы необходимых и
- 21. Действие подведения под понятие Например,
- 22. Выведение следствий Известно, что объект принадлежит
- 23. Прием выведения следствий на основе закона контрапозиции - важный логический прием
- 24. Примеры применения закона контрапозиции 1.
- 25. Классификация. Деление треугольников по углам
- 26. Список литературы1.Талызина Н.Ф. Педагогические технологии. Учебн. для
- 27. Автор шаблона:Ранько Елена Алексеевна учитель начальных классов МАОУ лицей №21 г. Иваново
Слайд 1Формирование математических
понятий
Учитель математики ГОУ ЯО
«Центр помощи детям»
Юстинова О.Б.
Слайд 2
Одной из задач развития математического образования в Российской
Понятия являются одной из главных составляющих в содержании любого предмета.
Понятие, усвоенное учеником, становится абстрактным и обобщенным образом, отражающим различные классы математических объектов.
Слайд 3Объем понятия
Объем понятия - это тот класс объектов, которые
Например, объем понятия треугольник —
все множество треугольников, независимо от их конкретных характеристик (видов углов, размеров сторон и др.)
Слайд 4Объем понятия
многоугольник:
множество
обыкновенная дробь:
правильные и неправильные дроби, положительные, отрицательные дроби.
Слайд 5Содержание понятия - та система существенных свойств (необходимых, достаточных признаков), по
Совокупность свойств, по которым объекты объединяются в единый класс, называются необходимыми и достаточными признаками.
Содержание понятия
Слайд 6Содержание понятия
Параллелограмм:
- выпуклый четырехугольник;
- стороны попарно параллельны и т.д.
Правильная дробь:
- обыкновенная
- числитель меньше знаменателя.
Треугольник:
- замкнутая ломаная;
-состоит из трех отрезков и т.д.
Слайд 7Виды понятий
Конъюнктивные понятия.
Признаки
вместе содержание, по которому объекты объединяются в единый класс.
Признаки связаны союзом «и».
Дизъюнктивные понятия.
Признаки не дополняют друг друга, а заменяют. Достаточно какого-то одного признака из всех перечисленных.
Признаки связаны союзом «или».
Слайд 8Правило заключения о принадлежности объекта к понятию с конъюнктивной структурой признаков:
-если объект не обладает хотя бы одним из признаков, он не относится к данному понятию ;
-если хотя бы про один из признаков ничего неизвестно, то при наличии остальных признаков неизвестно, принадлежит или не принадлежит объект к данному понятию.
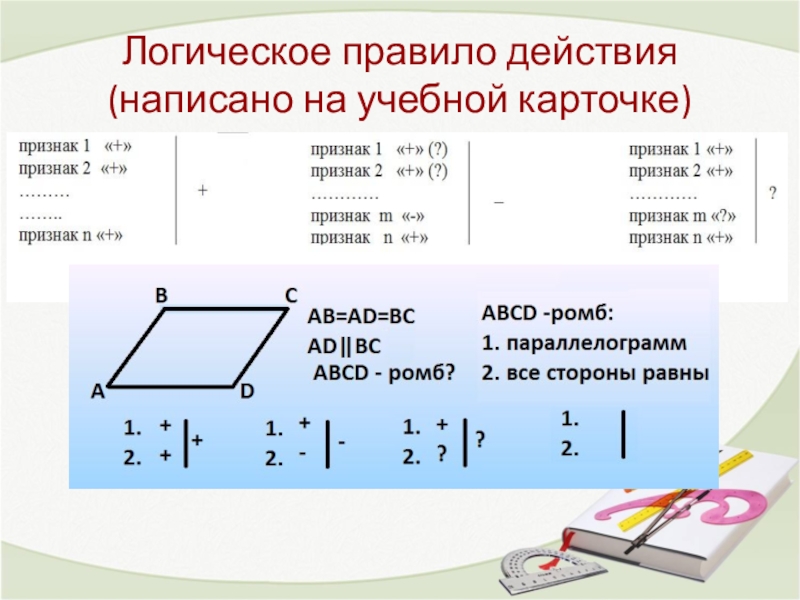
Слайд 9Логическое правило действия
(написано на учебной карточке)
+ наличие соответствующего признака
- отсутствие
? неизвестно (невозможно дать определенный ответ)
|+ предмет подходит под данное понятие
|- предмет не подходит под данное понятие
|? неизвестно, подходит или нет
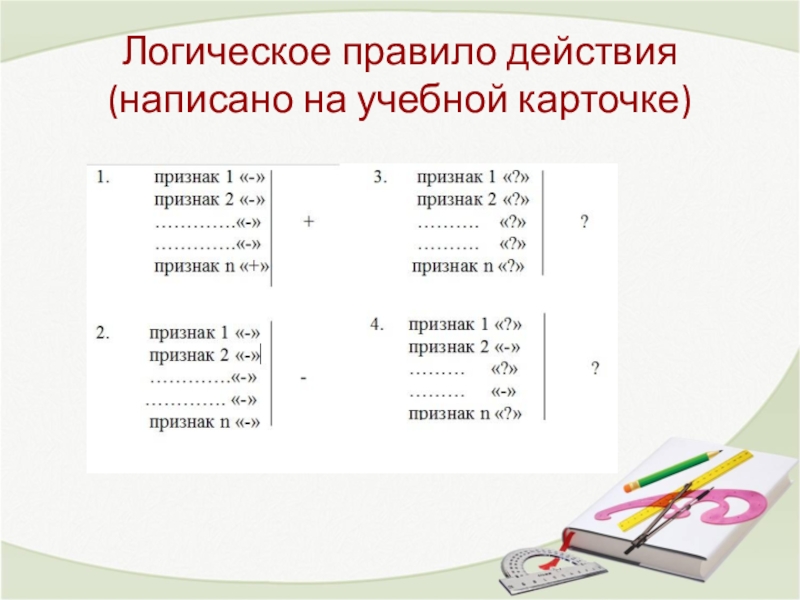
Слайд 11 Правило заключения о принадлежности объекта к данному понятию с дизъюнктивной структурой
-объект относится к данному понятию, если он обладает хотя бы одним признаком из числа альтернативных;
-если объект не обладает ни одним из этих признаков, он не относится к данному понятию ;
-если ни про один из признаков неизвестно, есть он или нет, то неизвестно, относится или не относится этот объект к данному понятию.
Слайд 13Примеры понятий
С дизъюнктивной структурой признаков
Неправильная дробь:
Числитель больше знаменателя или числитель равен
С конъюнктивной структурой признаков
Ромб — параллелограмм, у которого все стороны равны.
Слайд 14Абсолютные понятия
Абсолютные понятия объединяют предметы в классы по определенным
Например,
параллелограмм - четырехугольник , у которого стороны попарно параллельны.
Слайд 15Относительные понятия
Относительные понятия объединяют объекты в классы по свойствам,
Например:
1) В понятии перпендикулярные прямые фиксируется: две прямые, пересечение, образование при этом прямого угла.
2) Число-это отношение того, что подвергается количественной оценке(длина, вес, объем и др.)
к эталону, который используется
для этой оценки.
Слайд 16Относительные понятия
Число зависит и от измеряемой величины, и от
Относительные понятия вызывают у учащихся трудности, так как ученики не учитывают относительность понятий и оперируют с ними, как с абсолютными понятиями.
Слайд 17По степени обобщенности
Родовое понятие (более широкое) и видовое понятие.
Чем уже понятие, тем богаче его содержание.
Понятие определяется через
ближайшее родовое понятие .
Слайд 18Примеры
Четырехугольники — родовое понятие для параллелограмма; параллелограмм-видовое для четырехугольника;
параллелограмм—
прямоугольник ( ромб) — родовое понятие для квадрата.
Слайд 19
Виды действий, используемых при формировании понятий.
1. Действие распознавания,
2. Выведение следствий.
3. Сравнение.
4. Классификация.
5. Установление иерархических
отношений внутри системы понятий.
Слайд 20Действие подведения под понятие
-указание системы необходимых и достаточных свойств объектов данного
-установление , обладает ли данный объект выделенными свойствами или не обладает;
-заключение о принадлежности объекта к данному понятию.
Слайд 21Действие подведения под понятие
Например, чтобы доказать равенство углов,
-при наложении совпадают;
-состоят из равных частей;
-равные третьему равны;
-равные +равные =равны;
-равные -равные =равны;
-имеют равные градусные меры;
-соответствующие углы равных
треугольников и т.д.
Слайд 22Выведение следствий
Известно, что объект принадлежит данному классу. Из факта
Например, фигура является равнобедренным треугольником. Что можно сказать об этой фигуре? Какими свойствами она обладает?
Эти свойства называются необходимыми признаками.
Действие выведения следствия обогащает понятие треугольника, делает его более содержательным.
Слайд 24
Примеры применения закона контрапозиции
1. Если А, то В.
Если углы
2. Если не В, то не А.
Если углы не равны, то они не будут вертикальными.
3.Если не А, то вывод сделать нельзя.
Если углы не вертикальные, то о градусных мерах углов нельзя сделать вывод.
4. Если В, то вывод сделать нельзя.
Если углы равны, то какие это углы-неизвестно.
Слайд 25Классификация.
Деление треугольников по углам на остроугольные, прямоугольные, тупоугольные
Классификация треугольников по соотношению сторон: разносторонние треугольники, равнобедренные треугольники.
Равносторонний треугольник- следующий уровень этой классификации.
Слайд 26Список литературы
1.Талызина Н.Ф. Педагогические технологии. Учебн. для студ. сред. пед. учеб.
Электронный вариант
1.http://www.bsu.ru/content/page/1415/hecadem/talysina/talysina.pdf
2..МГУ им. М.В. Ломоносова. Формирование приемов математического мышления. Под редакцией Н.Ф. Талызиной. ТОО «Вентана-Граф», Москва, 1995