Тема урока:
Векторы в пространстве
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему: Векторы в пространстве
Содержание
- 1. Презентация по математике на тему: Векторы в пространстве
- 2. Слайд 2
- 3. Мало знать, надо и применять. Мало хотеть,
- 4. Цели урокаИзучить определение вектора в пространстве и связанные с ним понятия.Закрепить знания решением задач.
- 5. Слайд 5
- 6. Вектор развития веб -сайтаВектор развития личностиВектор развития мобильных приложений
- 7. Физические величиныСкорость Ускорение а
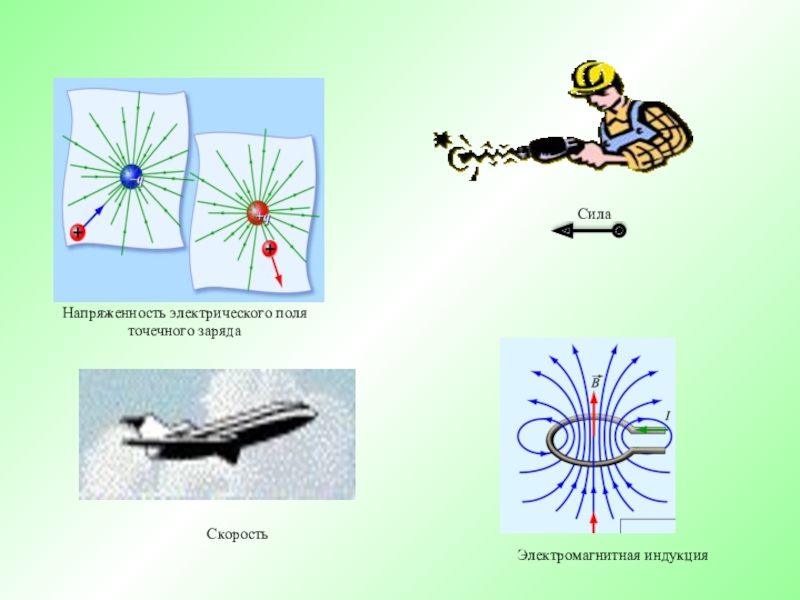
- 8. Напряженность электрического поля точечного зарядаСилаСкоростьЭлектромагнитная индукция
- 9. Понятие вектора появилось в 19 веке в работах математиков Г. Грассмана У. Гамильтона
- 10. Современная символика для обозначения вектора r была введена в 1853 году французским математиком О. Коши.
- 11. ЗаданиеЗаписать все термины по теме «Векторы на плоскости».
- 12. Термины по теме «Векторы на плоскости». ВекторНулевой векторДлина вектораКоллинеарные векторыСонаправленные векторыПротивоположно направленные векторыРавные векторы
- 13. Задание Заполнить таблицу: Задание Заполнить таблицу:
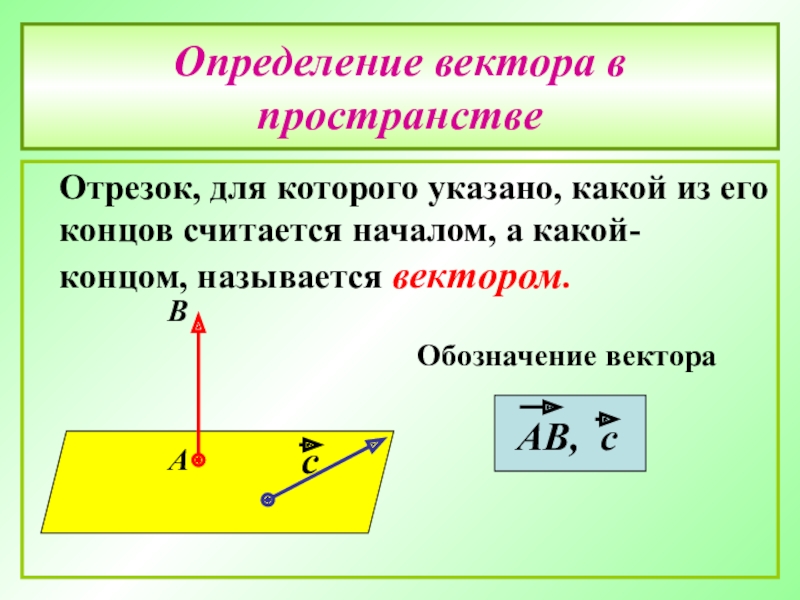
- 14. Определение вектора в пространстве Отрезок, для
- 15. ТТЛюбая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым.
- 16. Слайд 16
- 17. Длина вектора Длиной вектора АВ называется длина
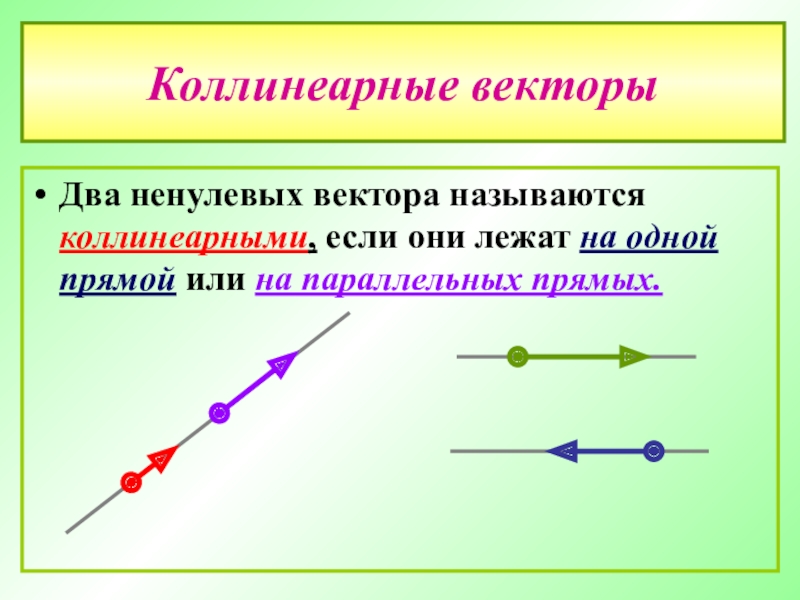
- 18. Коллинеарные векторы Два ненулевых вектора называются коллинеарными,
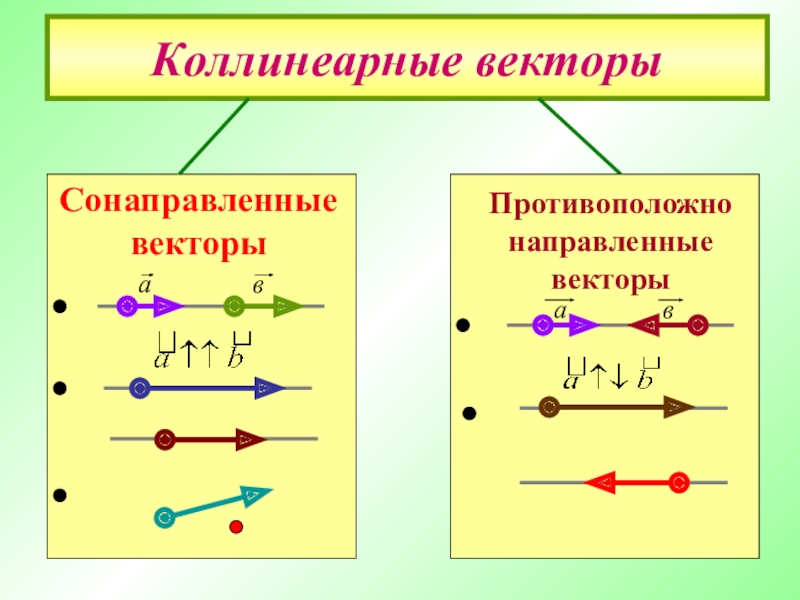
- 19. Коллинеарные векторыПротивоположно направленные векторыСонаправленные векторыавав
- 20. Какие векторы на рисунке сонаправленные? Какие векторы
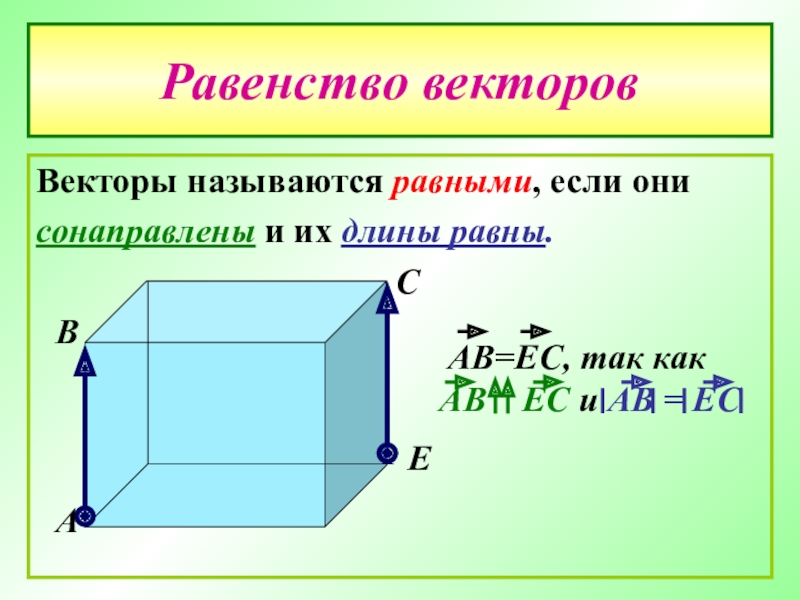
- 21. Равенство векторовВекторы называются равными, если они сонаправлены и их длины равны.АВСЕ
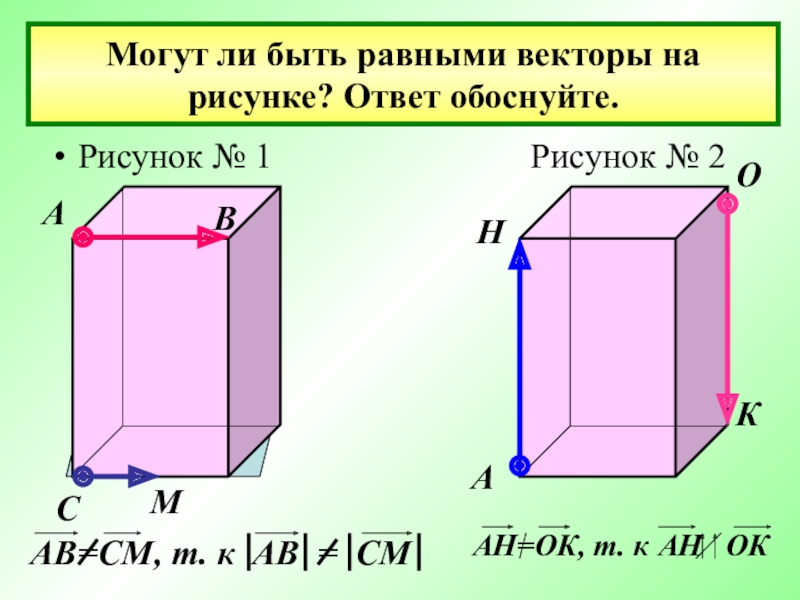
- 22. Могут ли быть равными векторы на рисунке?
- 23. Доказать, что от любой точки пространства можно
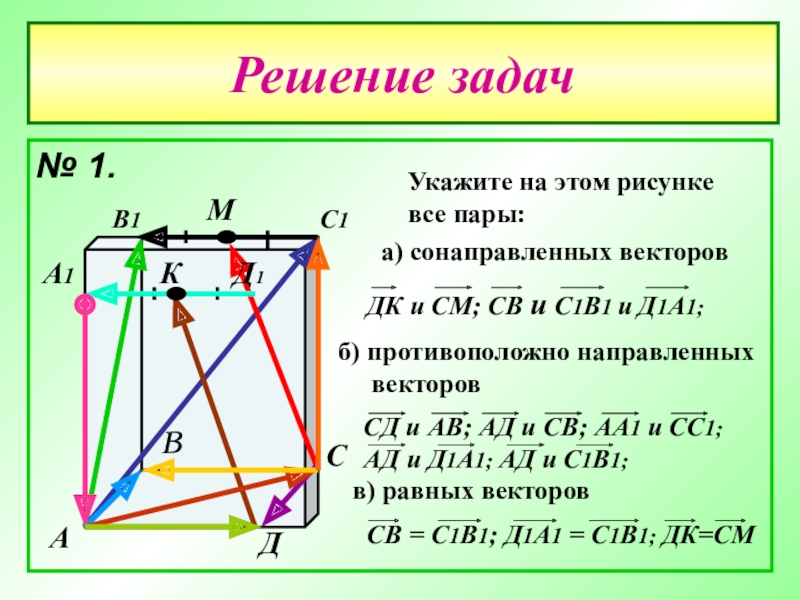
- 24. Решение задач№ 1.АВСДА1В1С1Д1МКУкажите на этом рисункевсе пары:а)
- 25. Решение задач№ 1.АВСДА1В1С1Д1МКУкажите на этом рисункевсе пары:а)
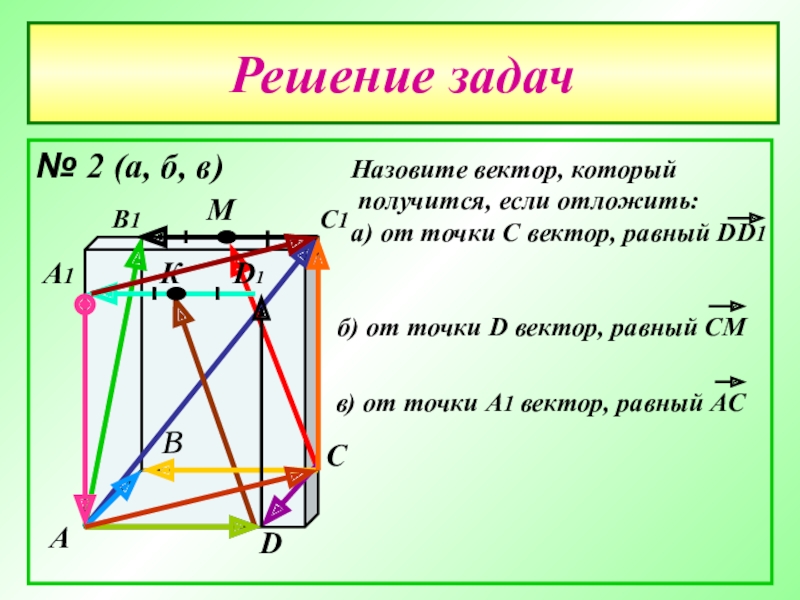
- 26. Решение задач№ 2 (а, б, в)АВСDА1В1С1D1МК
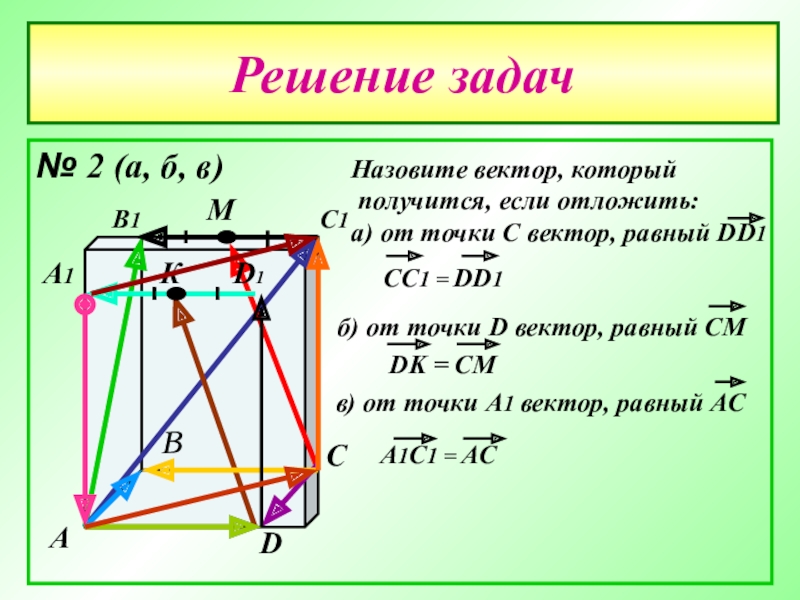
- 27. Решение задач№ 2 (а, б, в)АВСDА1В1С1D1МК
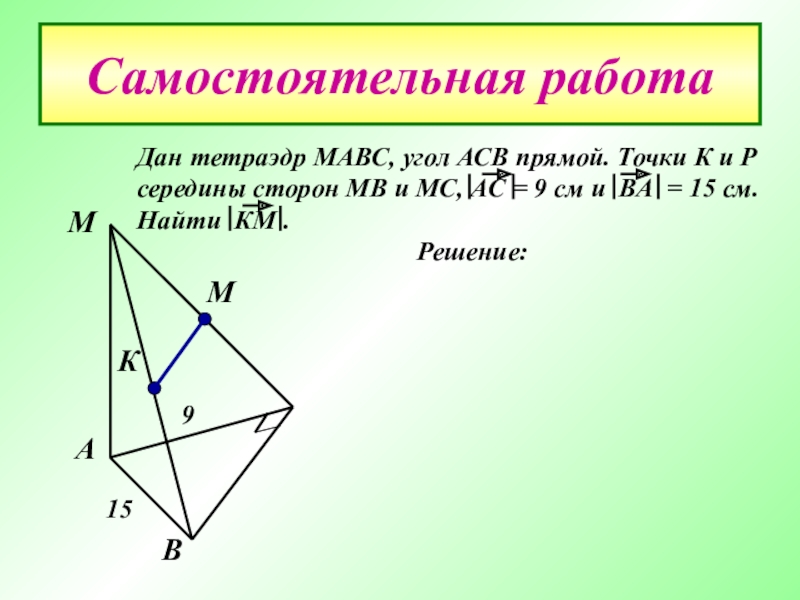
- 28. Самостоятельная работаДан тетраэдр МАВС, угол АСВ прямой.
- 29. Самостоятельная работаДан тетраэдр МАВС, угол АСВ прямой.
- 30. Слайд 30
- 31. Кроссворд1) Фамилия математика, в работе которого впервые
- 32. Кроссворд
- 33. АВСДА1В1С1Д1МКУкажите на этом рисункевсе пары:а) сонаправленных векторов б) противоположно направленных векторовв) равных векторовДомашнее задание
- 34. Цели урока:Изучить определение вектора в пространстве и
- 35. Мало знать, надо и применять. Мало хотеть,
- 36. Спасибо за урок!
Мало знать, надо и применять. Мало хотеть, надо и делать И Гете.Тема урока:
Слайд 3Мало знать, надо и применять.
Мало хотеть, надо и делать
И Гете.
Слайд 4Цели урока
Изучить определение вектора в пространстве и связанные с ним понятия.
Закрепить
знания решением задач.
Слайд 10Современная символика для обозначения вектора r была введена в 1853 году
французским математиком О. Коши.
Слайд 12Термины по теме «Векторы на плоскости».
Вектор
Нулевой вектор
Длина
вектора
Коллинеарные векторы
Сонаправленные векторы
Противоположно направленные векторы
Равные векторы
Коллинеарные векторы
Сонаправленные векторы
Противоположно направленные векторы
Равные векторы
Слайд 14Определение вектора в пространстве
Отрезок, для которого указано, какой из
его концов считается началом, а какой- концом, называется вектором.
Слайд 15ТТ
Любая точка пространства также
может рассматриваться как вектор. Такой вектор называется
нулевым.
Слайд 17
Длина вектора
Длиной вектора АВ называется длина отрезка АВ.
Длина вектора АВ
(вектора а) обозначается так:
АВ , а
Длина нулевого вектора считается равной нулю:
АВ , а
Длина нулевого вектора считается равной нулю:
0
= 0
Слайд 18Коллинеарные векторы
Два ненулевых вектора называются коллинеарными, если они лежат на
одной прямой или на параллельных прямых.
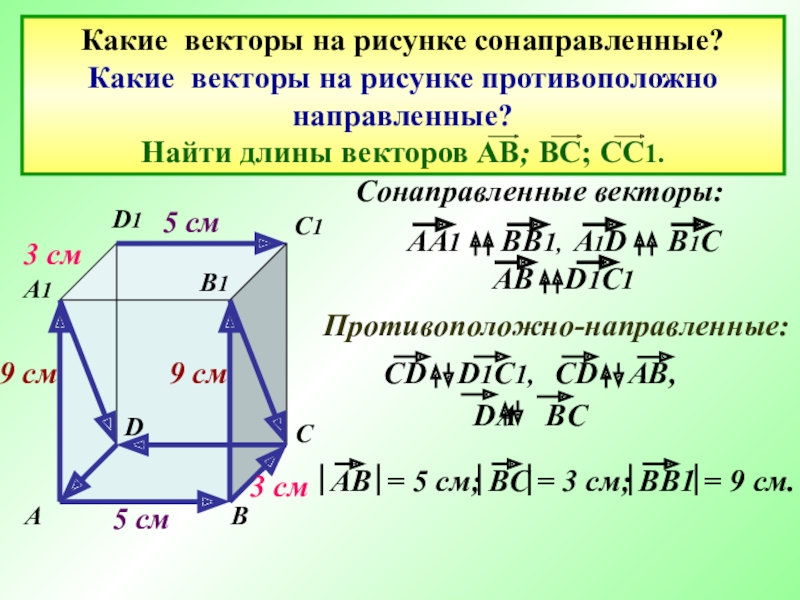
Слайд 20Какие векторы на рисунке сонаправленные? Какие векторы на рисунке противоположно направленные? Найти длины
векторов АВ; ВС; СС1.
A
B
C
D
В1
D1
A1
C1
Сонаправленные векторы:
Противоположно-направленные:
5 см
3 см
9 см
5 см
3 см
9 см
Слайд 23
Доказать, что от любой точки пространства можно отложить вектор, равный данному,
и притом только один
Дано: а, М.
Доказать: в = а, М в, единственный.
Доказательство:
Проведем через вектор а и точку
М плоскость.
М
К
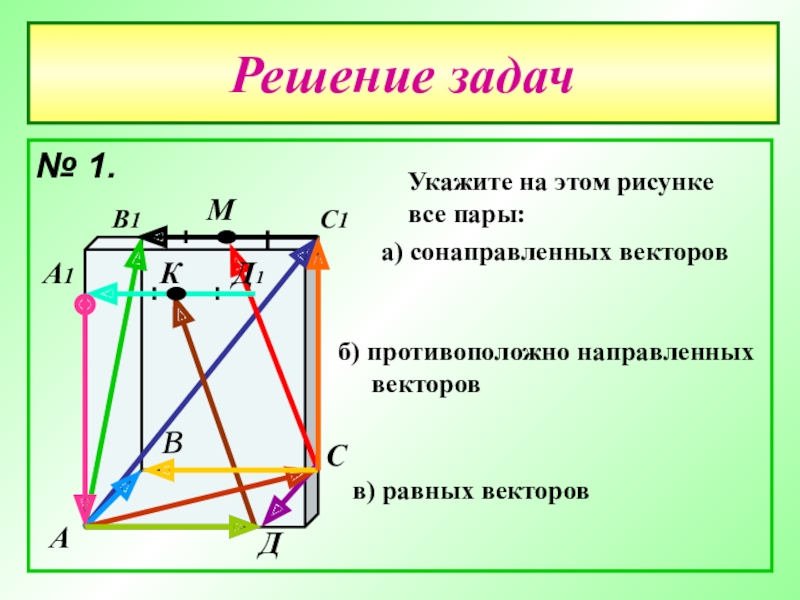
Слайд 24Решение задач
№ 1.
А
В
С
Д
А1
В1
С1
Д1
М
К
Укажите на этом рисунке
все пары:
а) сонаправленных векторов
б) противоположно
направленных
векторов
векторов
в) равных векторов
Слайд 25Решение задач
№ 1.
А
В
С
Д
А1
В1
С1
Д1
М
К
Укажите на этом рисунке
все пары:
а) сонаправленных векторов
б) противоположно
направленных
векторов
векторов
в) равных векторов
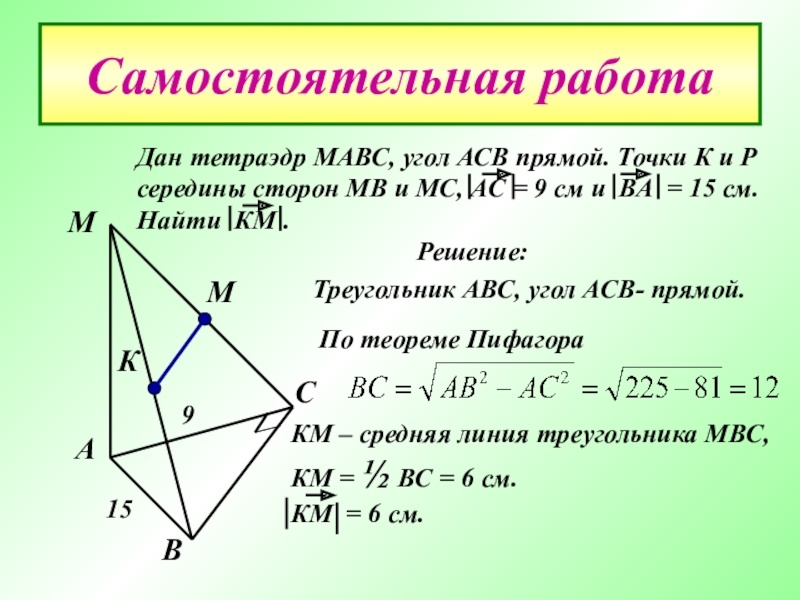
Слайд 28Самостоятельная работа
Дан тетраэдр МАВС, угол АСВ прямой. Точки К и Р
середины сторон МВ и МС, АС = 9 см и ВА = 15 см. Найти КМ .
Решение:
Решение:
М
А
В
К
М
9
15
Слайд 29Самостоятельная работа
Дан тетраэдр МАВС, угол АСВ прямой. Точки К и Р
середины сторон МВ и МС, АС = 9 см и ВА = 15 см. Найти КМ .
Решение:
Решение:
М
А
В
С
К
М
Треугольник АВС, угол АСВ- прямой.
9
15
Слайд 30
pingina.ru
Учебно – методические материалы
Студентам 1 курса
Тест по теме «Координаты и векторы»
Тест
Слайд 31Кроссворд
1) Фамилия математика, в работе которого впервые появилось понятие вектора.
2)
Как называется отрезок, для которого указано начало, конец и направление?
3) Название двух ненулевых векторов, лежащих на одной прямой или на двух параллельных прямых.
4) Математик, который ввел современное обозначение вектора.
5) Как называется расстояние между точками А и В у вектора АВ?
6) Как называются два вектора, если они сонаправлены, и их длины равны?
7) Векторная величина в физике.
7) Векторная величина в физике.
Слайд 33
А
В
С
Д
А1
В1
С1
Д1
М
К
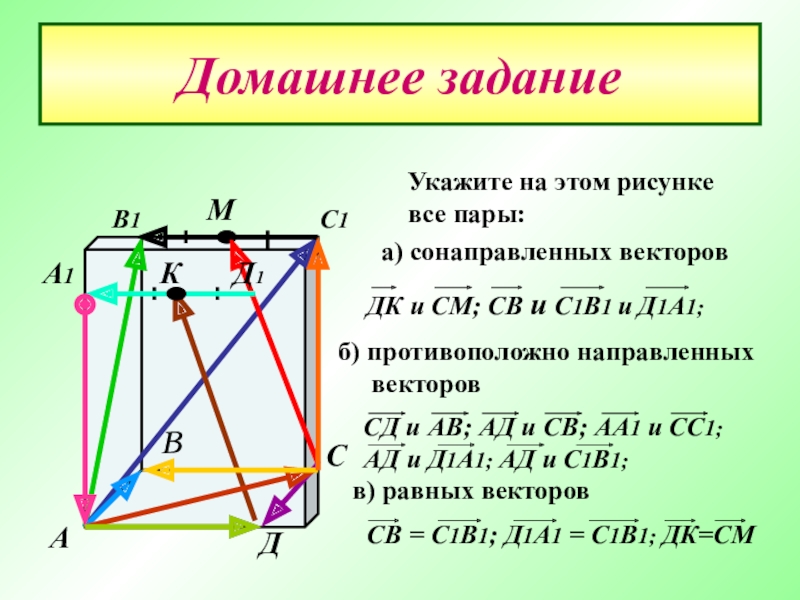
Укажите на этом рисунке
все пары:
а) сонаправленных векторов
б) противоположно направленных
векторов
в) равных векторов
Домашнее задание
Слайд 34Цели урока:
Изучить определение вектора в пространстве и связанные с ним понятия.
Закрепить
знания решением задач.
Тема урока: Векторы в пространстве
Слайд 35Мало знать, надо и применять.
Мало хотеть, надо и делать
И Гете.
Тема урока:
Векторы в пространстве
