- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему: Угол между прямыми.
Содержание
- 1. Презентация по математике на тему: Угол между прямыми.
- 2. Угол, образованный между пересекающимися прямыми. А)
- 3. Вывод:За угол между пересекающимися прямыми берут острый угол, если не оговорено дополнительное условие.
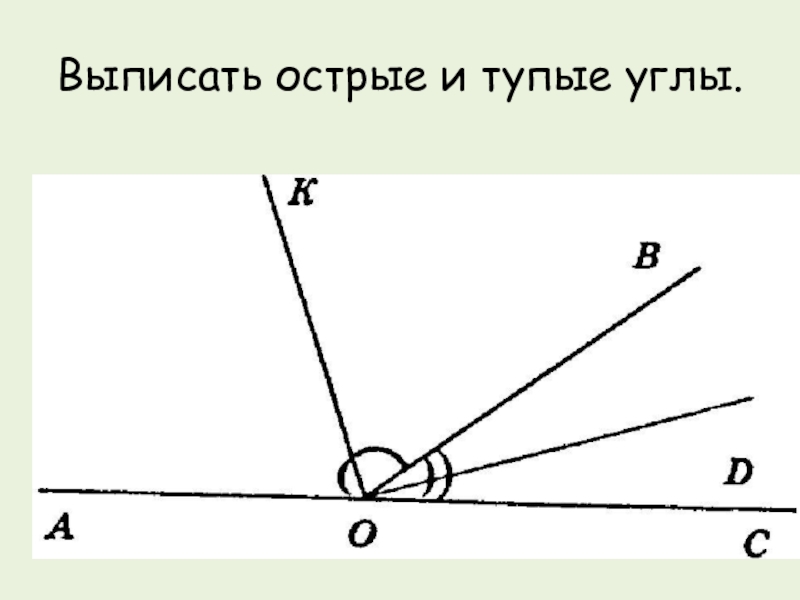
- 4. Выписать острые и тупые углы.
- 5. Повторим: теорема косинусов.Квадрат стороны треугольника равен сумме
- 6. ТеоремаЕсли одна прямая из двух лежит в
- 7. Угол между скрещивающимися прямыми.АВ и CD
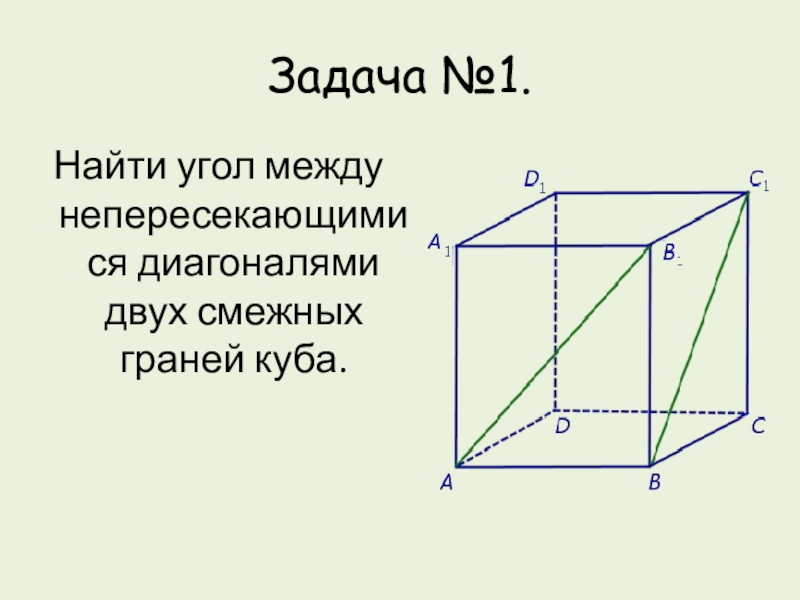
- 8. Задача №1.Найти угол между непересекающимися диагоналями двух смежных граней куба.
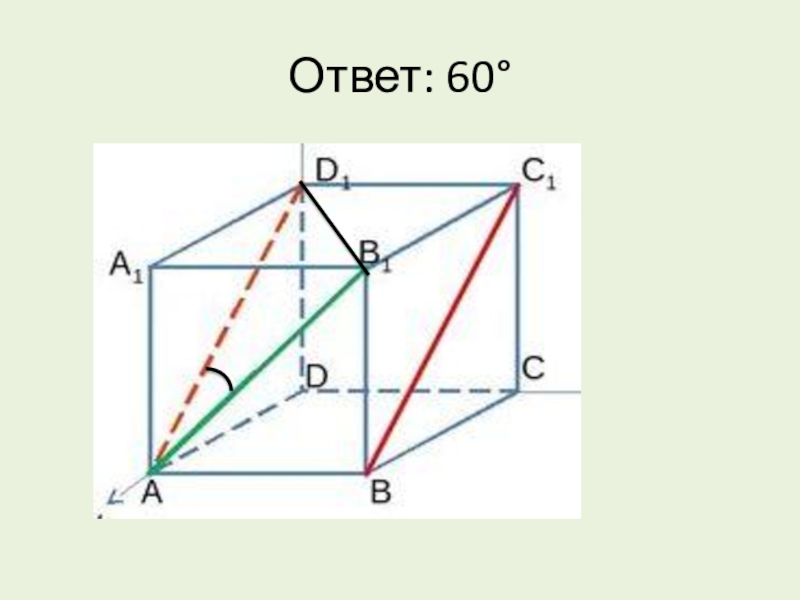
- 9. Ответ: 60°
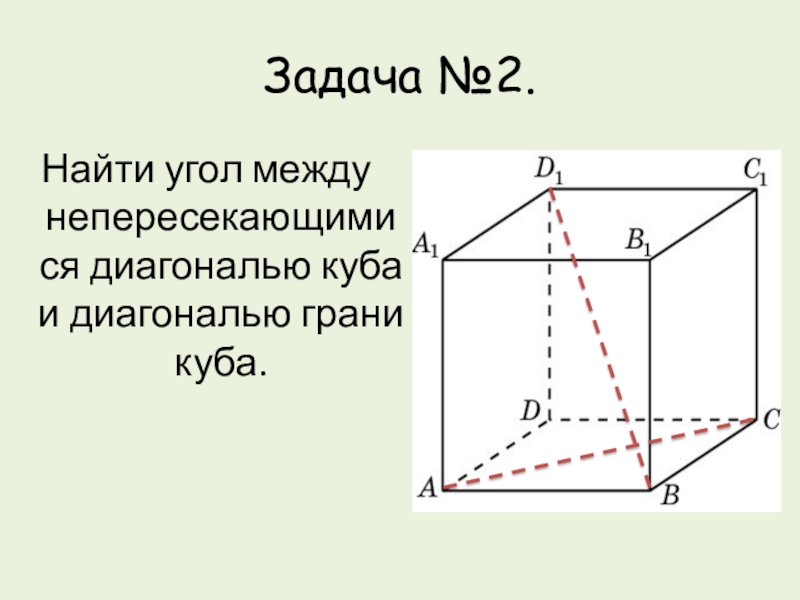
- 10. Задача №2.Найти угол между непересекающимися диагональю куба и диагональю грани куба.
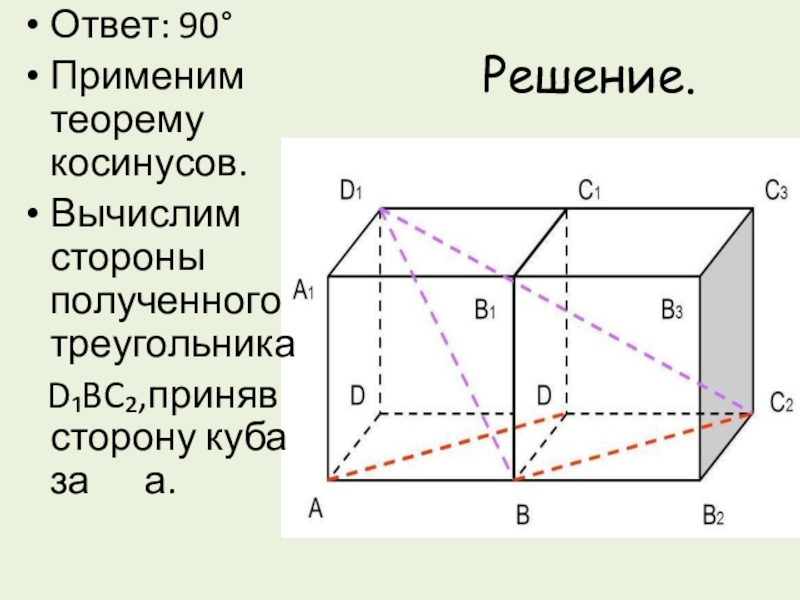
- 11. Решение.Ответ: 90°Применим теорему косинусов.Вычислим стороны полученного треугольника D₁BC₂,приняв сторону куба за а.
- 12. Теорема о трех косинусах.Cosϕ=coscos - величина угла
- 13. Задача №3. Решить задачу №2, применяя теорему
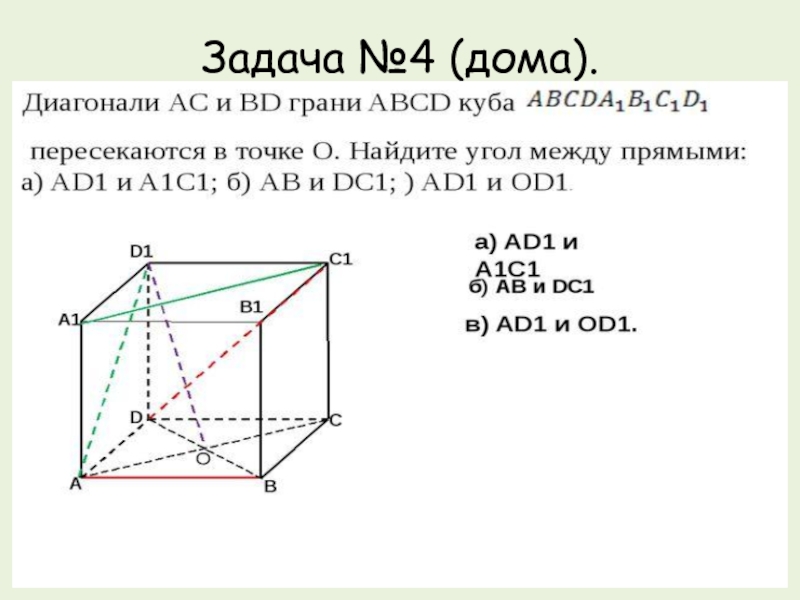
- 14. Задача №4 (дома).
- 15. Рефлексия.1. Понятие скрещивающихся прямых2. Могут ли быть
- 16. Слайд 16
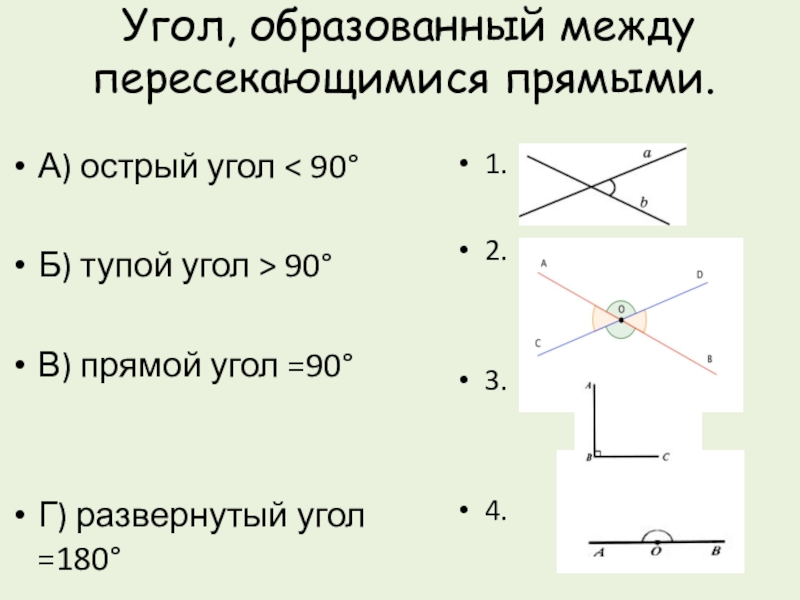
Угол, образованный между пересекающимися прямыми. А) острый угол < 90°Б) тупой угол > 90°В) прямой угол =90°Г) развернутый угол =180°1. 2. 3.4.
Слайд 2 Угол, образованный между пересекающимися прямыми.
А) острый угол < 90°
Б)
тупой угол > 90°
В) прямой угол =90°
Г) развернутый угол =180°
В) прямой угол =90°
Г) развернутый угол =180°
1.
2.
3.
4.
Слайд 3Вывод:
За угол между пересекающимися прямыми берут острый угол, если не оговорено
дополнительное условие.
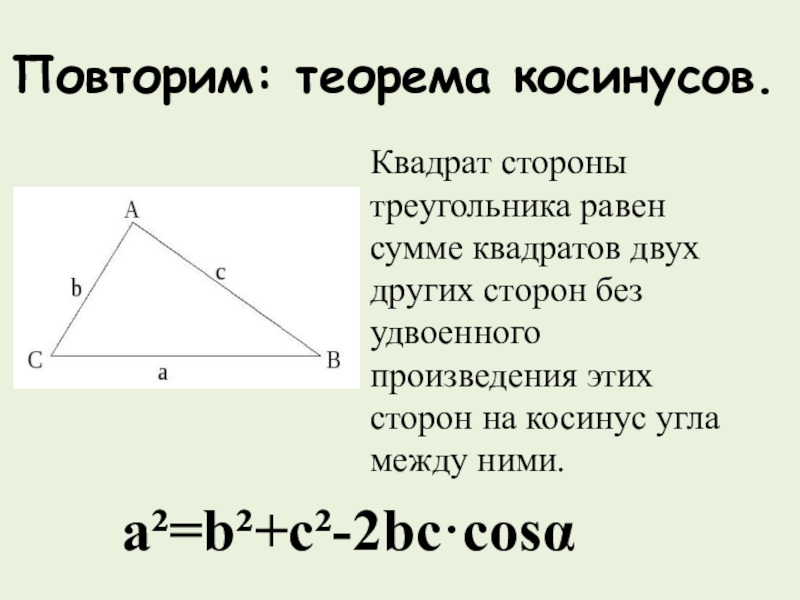
Слайд 5Повторим: теорема косинусов.
Квадрат стороны треугольника равен сумме квадратов двух других сторон
без удвоенного произведения этих сторон на косинус угла между ними.
a²=b²+c²-2bc·cosα
Слайд 6Теорема
Если одна прямая из двух лежит в плоскости, а другая пересекает
эту плоскость в точке, не лежащей на первой прямой то эти прямые скрещивающиеся.
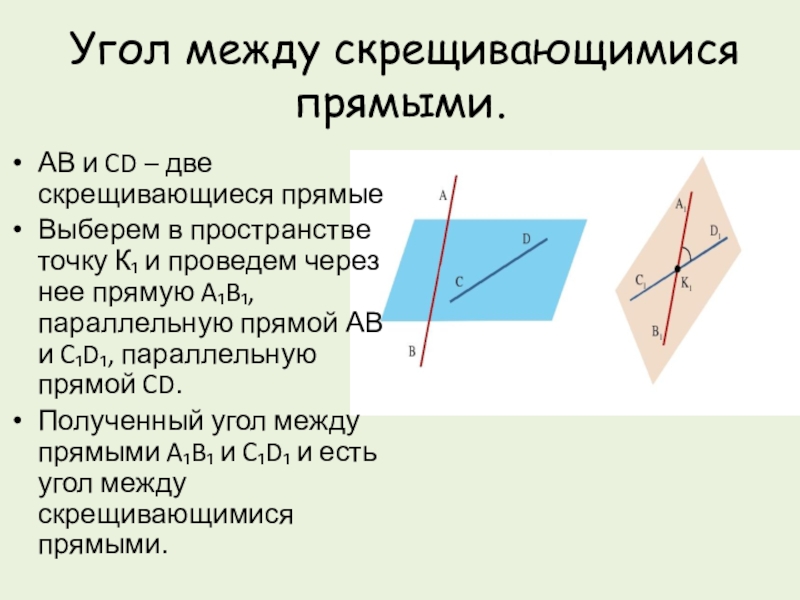
Слайд 7 Угол между скрещивающимися прямыми.
АВ и CD – две скрещивающиеся прямые
Выберем
в пространстве точку К₁ и проведем через нее прямую A₁B₁, параллельную прямой АВ и C₁D₁, параллельную прямой CD.
Полученный угол между прямыми A₁B₁ и C₁D₁ и есть угол между скрещивающимися прямыми.
Полученный угол между прямыми A₁B₁ и C₁D₁ и есть угол между скрещивающимися прямыми.
Слайд 11Решение.
Ответ: 90°
Применим теорему косинусов.
Вычислим стороны полученного треугольника
D₁BC₂,приняв сторону куба
за а.
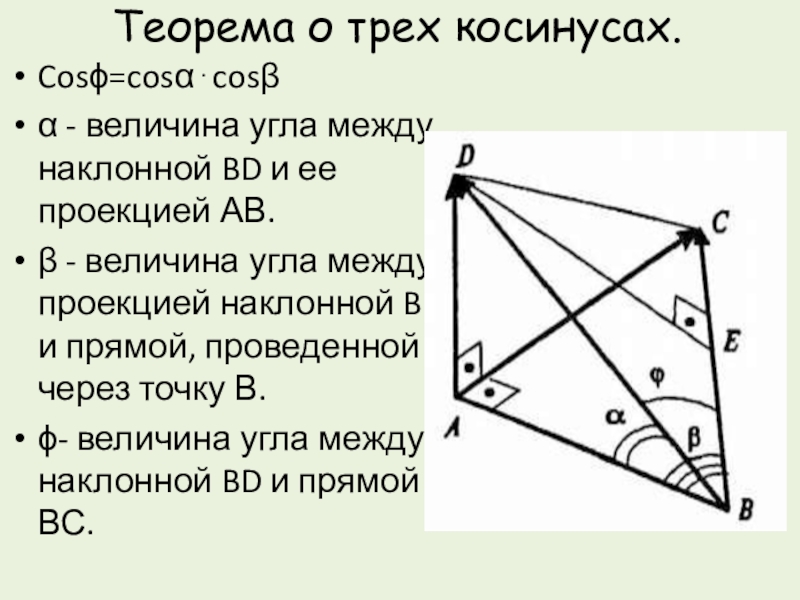
Слайд 12Теорема о трех косинусах.
Cosϕ=coscos
- величина угла между наклонной BD и
ее проекцией АВ.
- величина угла между проекцией наклонной BD и прямой, проведенной через точку В.
ϕ- величина угла между наклонной BD и прямой ВС.
- величина угла между проекцией наклонной BD и прямой, проведенной через точку В.
ϕ- величина угла между наклонной BD и прямой ВС.
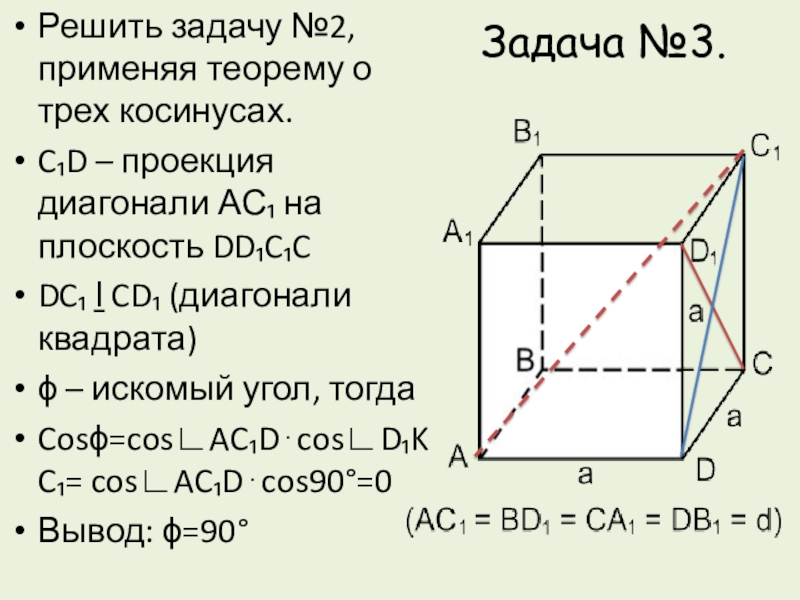
Слайд 13Задача №3.
Решить задачу №2, применяя теорему о трех косинусах.
C₁D –
проекция диагонали АС₁ на плоскость DD₁C₁C
DC₁ ḻ CD₁ (диагонали квадрата)
ϕ – искомый угол, тогда
Cosϕ=cos∟AC₁Dcos∟D₁KC₁= cos∟AC₁Dcos90°=0
Вывод: ϕ=90°
DC₁ ḻ CD₁ (диагонали квадрата)
ϕ – искомый угол, тогда
Cosϕ=cos∟AC₁Dcos∟D₁KC₁= cos∟AC₁Dcos90°=0
Вывод: ϕ=90°
Слайд 15Рефлексия.
1. Понятие скрещивающихся прямых
2. Могут ли быть скрещивающиеся прямые а и
в параллельными прямой с?
3. как определить угол между скрещивающимися прямыми?
4. теорема о трех косинусах?
5. что сложно было?
3. как определить угол между скрещивающимися прямыми?
4. теорема о трех косинусах?
5. что сложно было?