- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Цилиндр.Конус.Усеченный конус.Шар
Содержание
- 1. Презентация по математике на тему Цилиндр.Конус.Усеченный конус.Шар
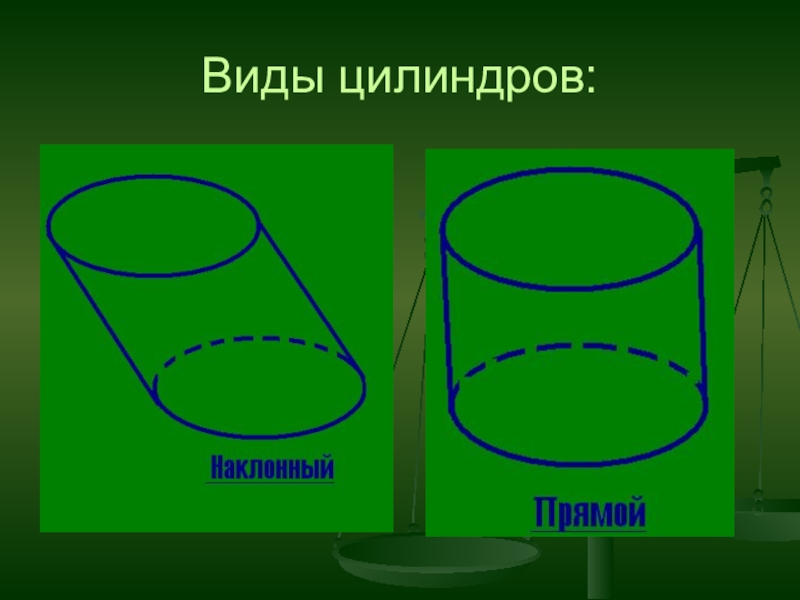
- 2. Виды цилиндров:
- 3. Определение цилиндра:Цилиндр – это тело, которое состоит
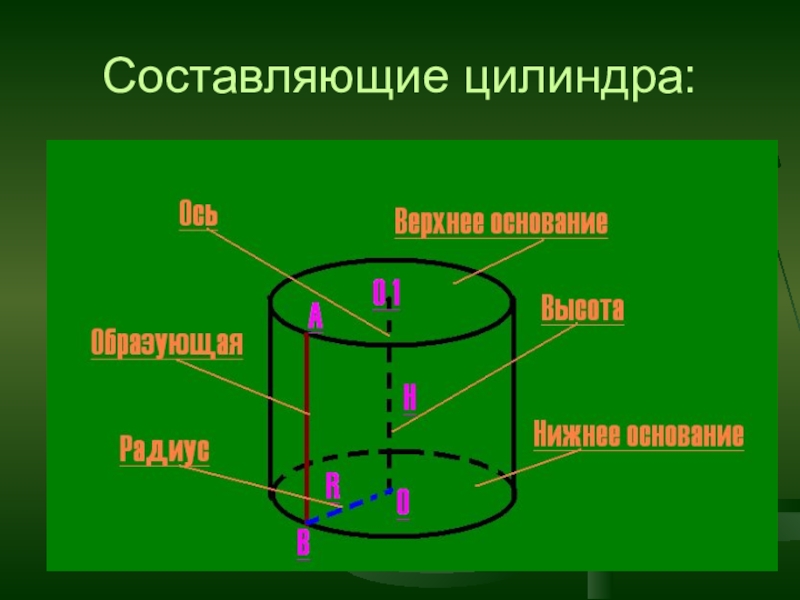
- 4. Составляющие цилиндра:
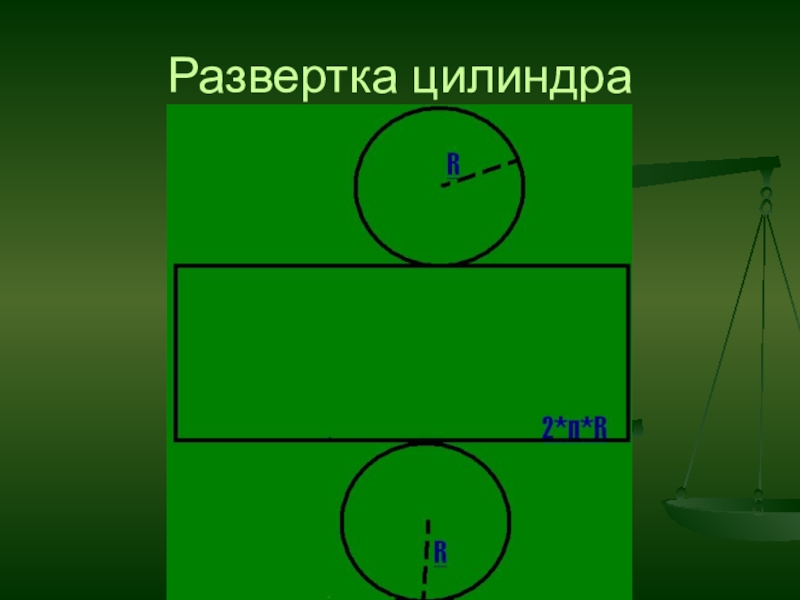
- 5. Развертка цилиндра
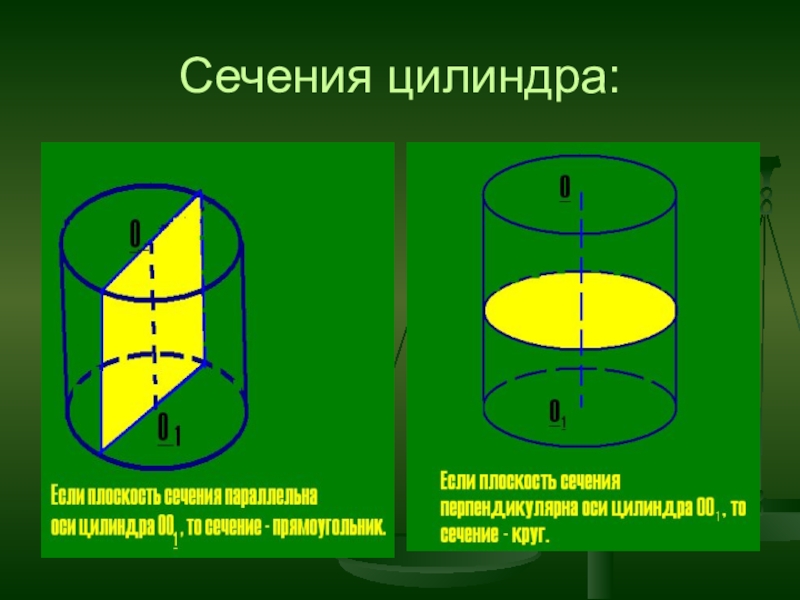
- 6. Сечения цилиндра:
- 7. Основные формулы:Sоснов= пR2Sбок =2пRHSполн = пR2+2пRH V= Sоснов* H = пR2 H
- 8. Слайд 8
- 9. Слайд 9
- 10. Задача: высота цилиндра равна 12 см, а
- 11. Конус.
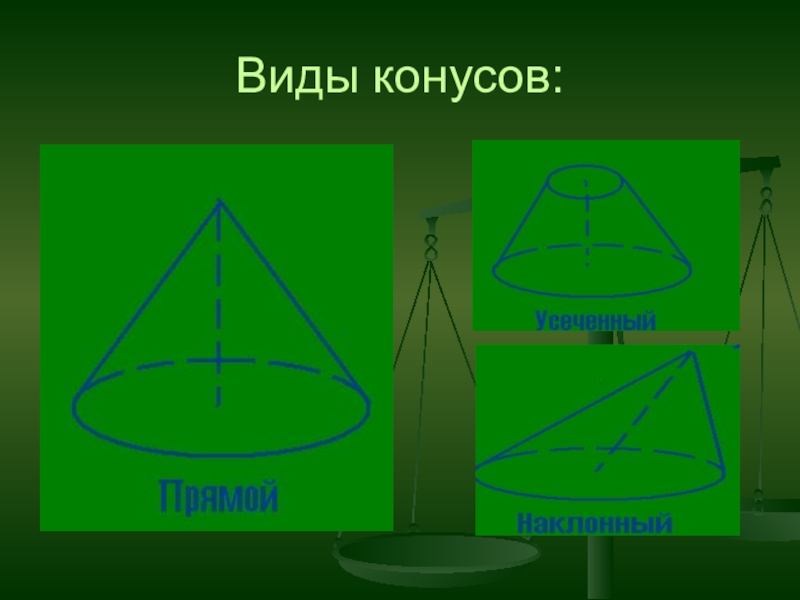
- 12. Виды конусов:
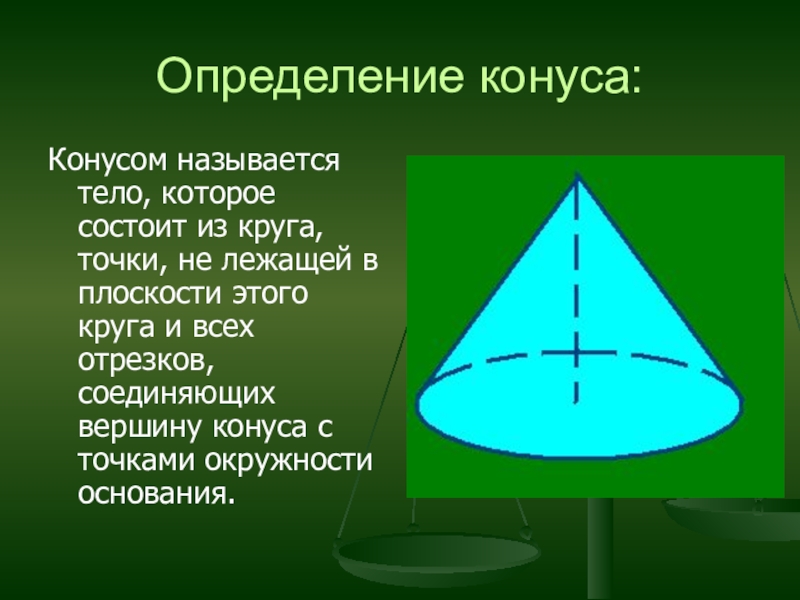
- 13. Определение конуса:Конусом называется тело, которое состоит из
- 14. Определение усеченного конуса:Усеченным конусом называется тело вращения, образованное вращением прямоугольной трапеции около боковой стороны, перпендикулярной основаниям.
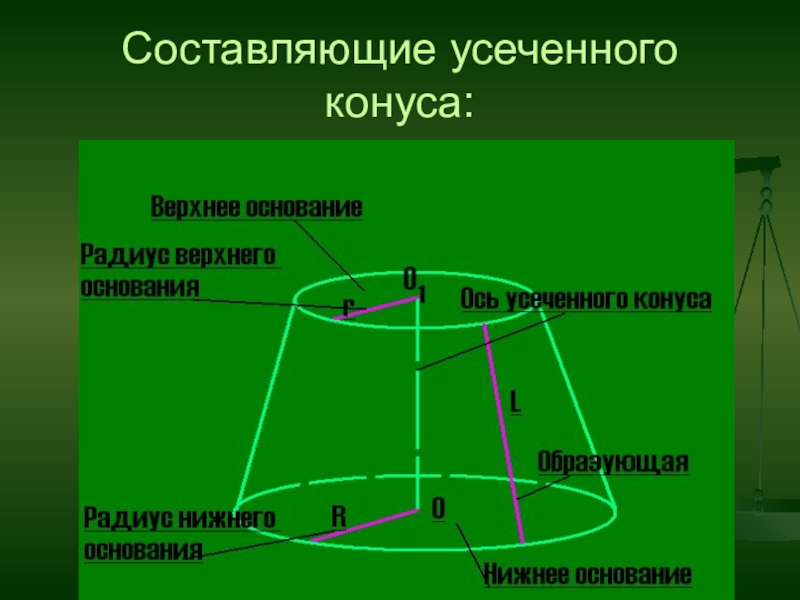
- 15. Составляющие усеченного конуса:
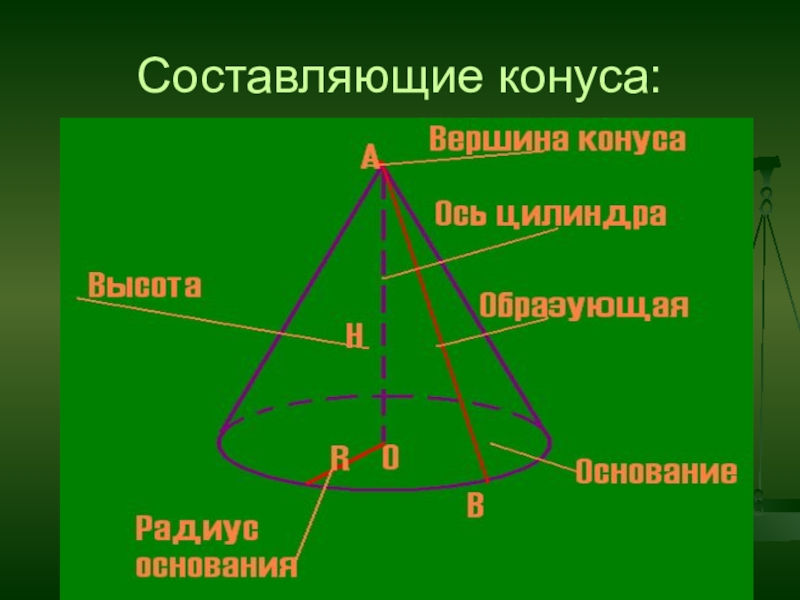
- 16. Составляющие конуса:
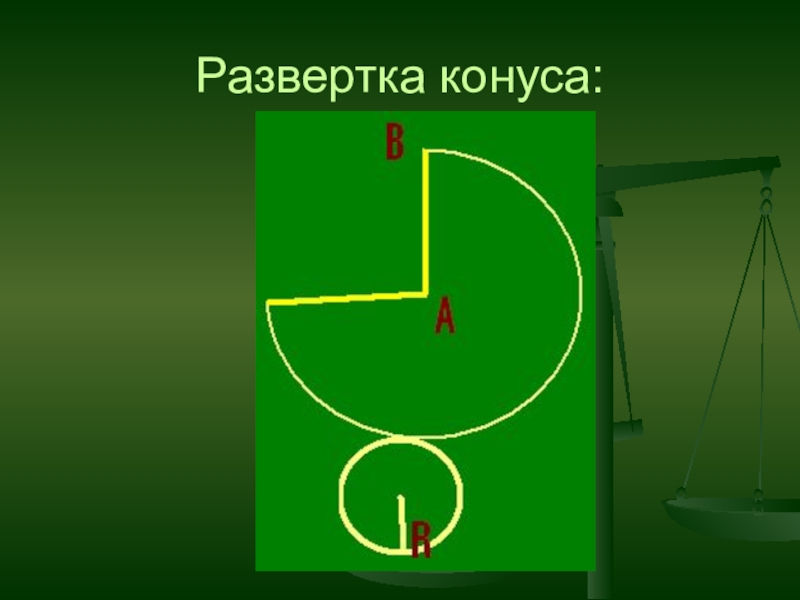
- 17. Развертка конуса:
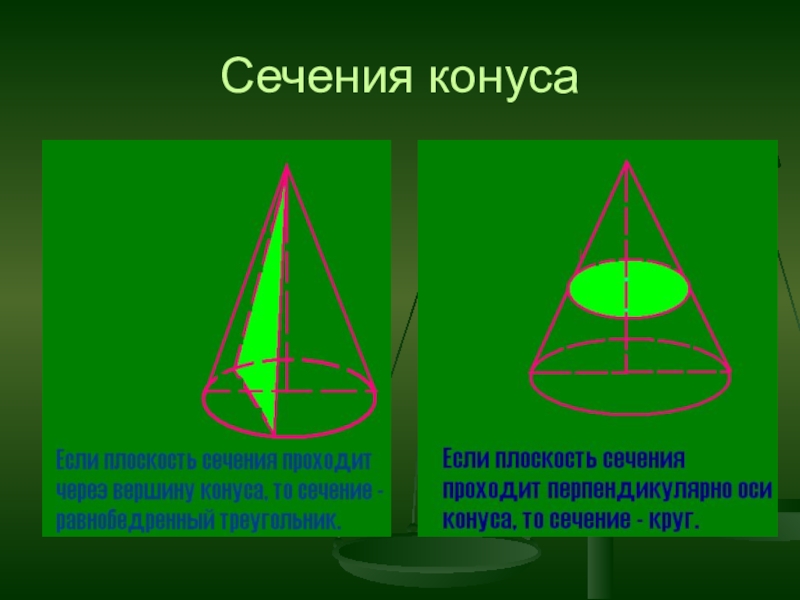
- 18. Сечения конуса
- 19. Основные формулы:Конус:Sбок = пRLSполн= пR(L+R)V=1/3пR2HУсеченный конус:Sбок = п(R+r)L
- 20. Слайд 20
- 21. Задача: высота конуса = 15 см, а
- 22. Шар
- 23. Определение шара:Сфера – поверхность, состоящая из всех
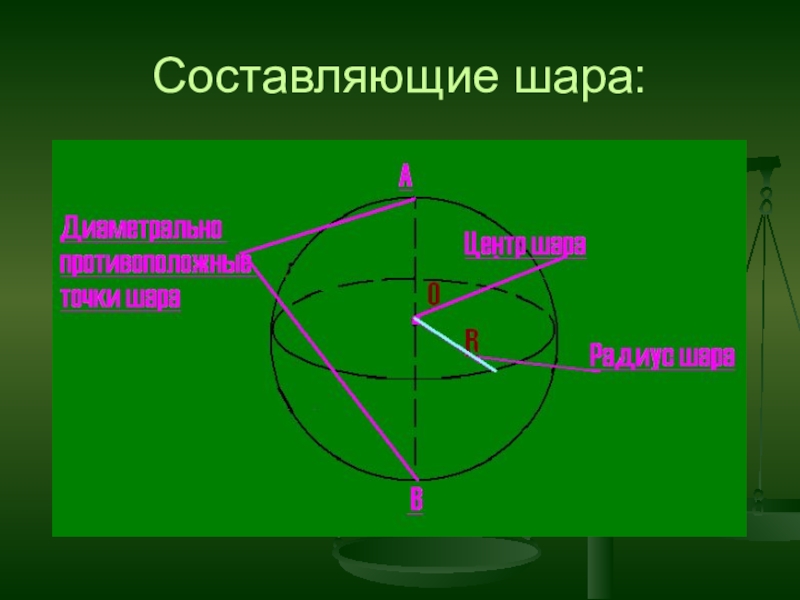
- 24. Составляющие шара:
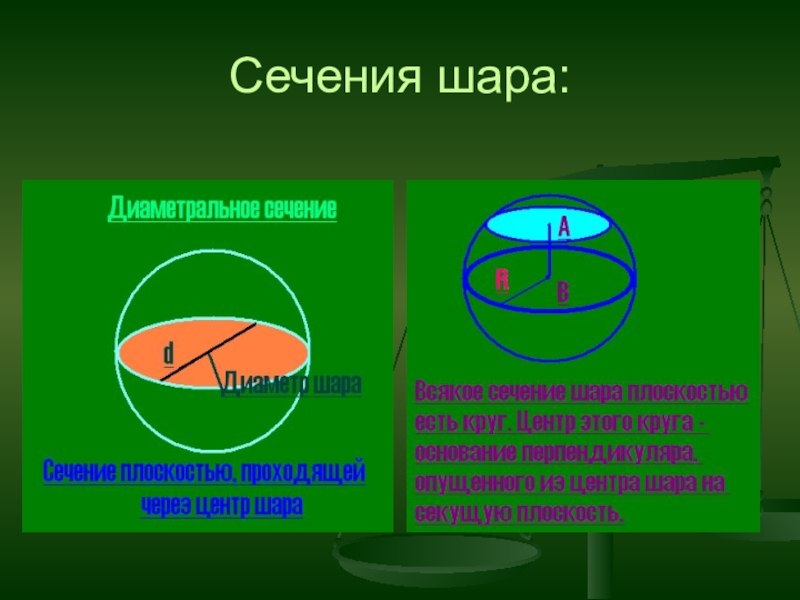
- 25. Сечения шара:
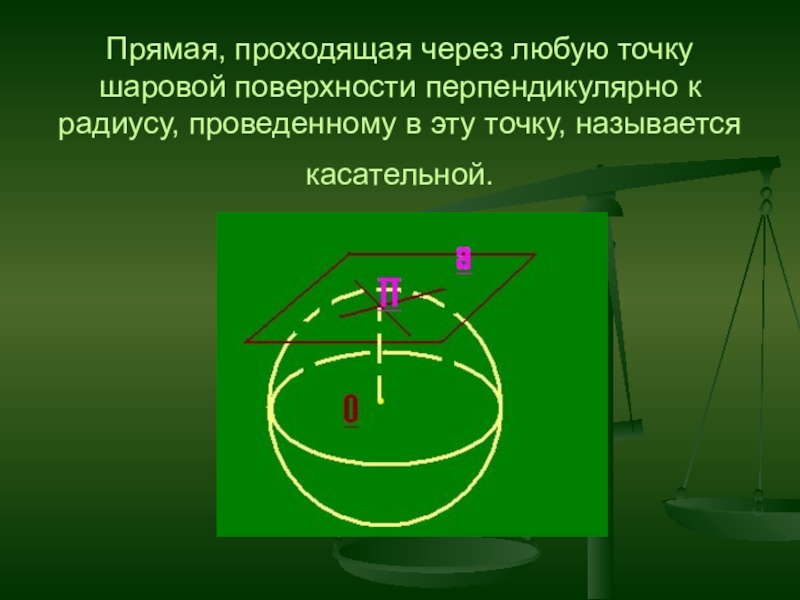
- 26. Прямая, проходящая через любую точку
- 27. Слайд 27
- 28. Основные формулы:Шар:Sполн = 4пR2V = 4/3пR3Шаровой сегмент:V
- 29. Задача: дан шар, радиус которого равен 25
- 30. В подготовке данной презентации нам помогли
- 31. Внесите верный вариант ответа в таблицу. В
- 32. Вариант 1 №1 Осевое сечение цилиндра –
- 33. Вариант 2 №1 Осевое
Слайд 3Определение цилиндра:
Цилиндр – это тело, которое состоит из двух кругов, совмещаемых
Слайд 8 При решении геометрических задач часто приходится рассматривать комбинации многогранников, в частности
Слайд 9 Призмой, вписанной в цилиндр, называется призма, основание которой – равные многоугольники,
Слайд 10Задача: высота цилиндра равна 12 см, а радиус основания –
Решение: формула площади боковой поверхности цилиндра - Sбок =2пRH.
R= 10 см,
H= 12 см
Sбок = 2п*10*12=240п см2.
Ответ: 240п см2.
Слайд 13Определение конуса:
Конусом называется тело, которое состоит из круга, точки, не лежащей
Слайд 14Определение усеченного конуса:
Усеченным конусом называется тело вращения, образованное вращением прямоугольной трапеции
Слайд 20 Пирамида описана около конуса, если ее основание – многоугольник, описанный около
Слайд 21Задача: высота конуса = 15 см, а радиус основания – 8
Решение: Так как высота конуса перпендикулярна к его основанию, то используя теорему Пифагора, получим: а2 = b2 + c2.
Где а- образующая,
b – высота,
C – радиус основания.
а = 17 см.
Ответ: 17см.
Слайд 23Определение шара:
Сфера – поверхность, состоящая из всех точек пространства, расположенных на
Шар – тело, ограниченное сферой.
Слайд 26 Прямая, проходящая через любую точку шаровой поверхности перпендикулярно к радиусу, проведенному
Слайд 27 Шаровой сегмент – часть шара, отсекаемая от него плоскостью. Шаровой слой –
Слайд 28Основные формулы:
Шар:
Sполн = 4пR2
V = 4/3пR3
Шаровой сегмент:
V = пН2(R –1/3H)
Sполн =
Шаровой сегмент:
V = 2/3пR2H
Sполн= пR(2H+(2RH-H2) 1/2)
Слайд 29Задача: дан шар, радиус которого равен 25 см, найти площадь полной
Решение: используя формулу площади полной поверхности шара, имеем –
Sполн = 4п25 см = 100п см2
Ответ: 100п см2