- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Теорема Менелая
Содержание
- 1. Презентация по математике на тему Теорема Менелая
- 2. • Исследовательская работа «Теорема Менелая» посвящена одной
- 3. • Гипотеза: знание особых свойств и подходов
- 4. Менелай Александрийский (1 век н.э.) написал «Сферику»
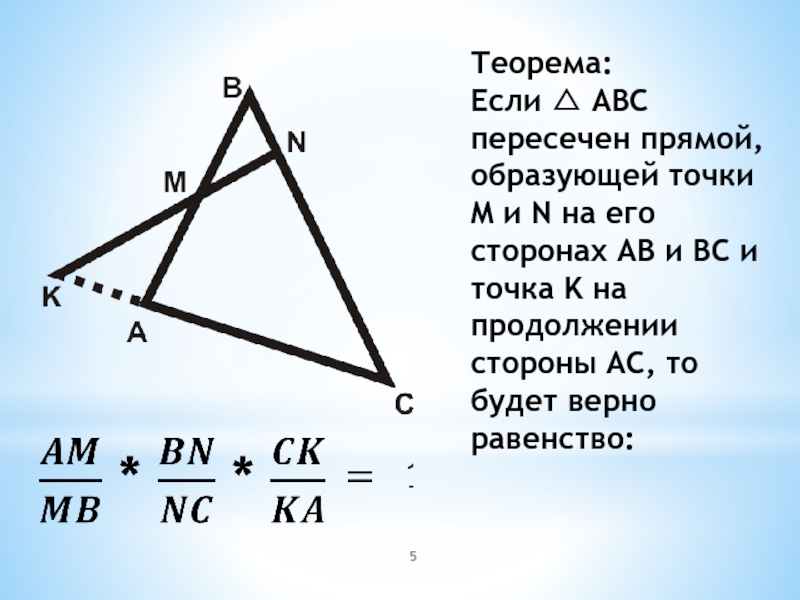
- 5. Теорема:Если △ ABC пересечен прямой, образующей точки
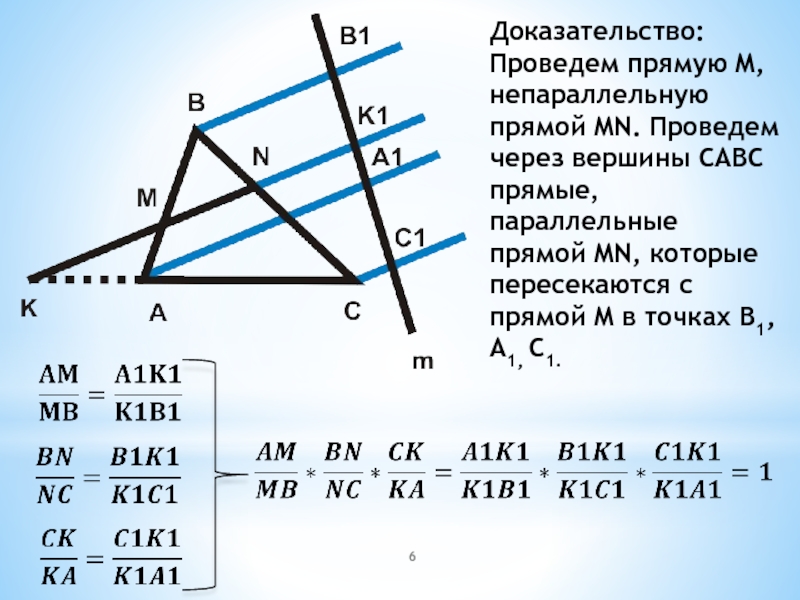
- 6. Доказательство:Проведем прямую M, непараллельную прямой MN. Проведем
- 7. Слайд 7
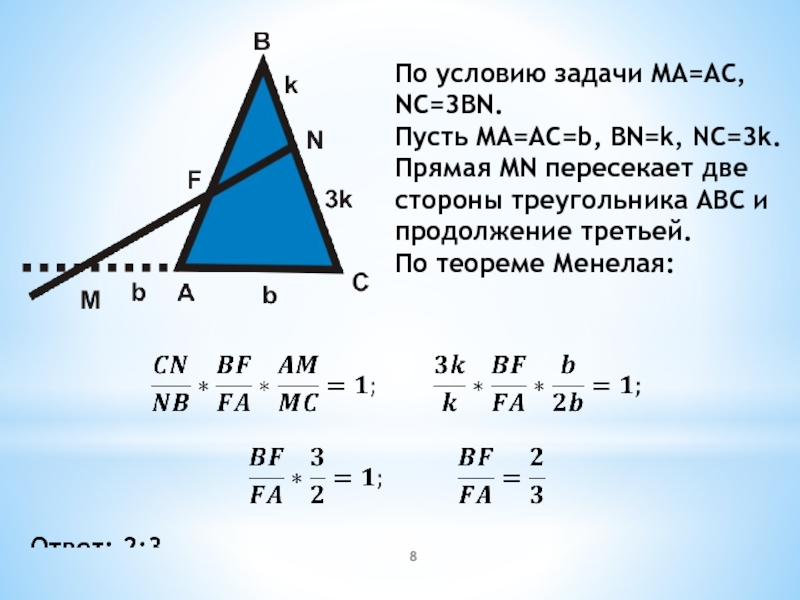
- 8. По условию задачи MA=AC, NC=3BN.Пусть MA=AC=b, BN=k,
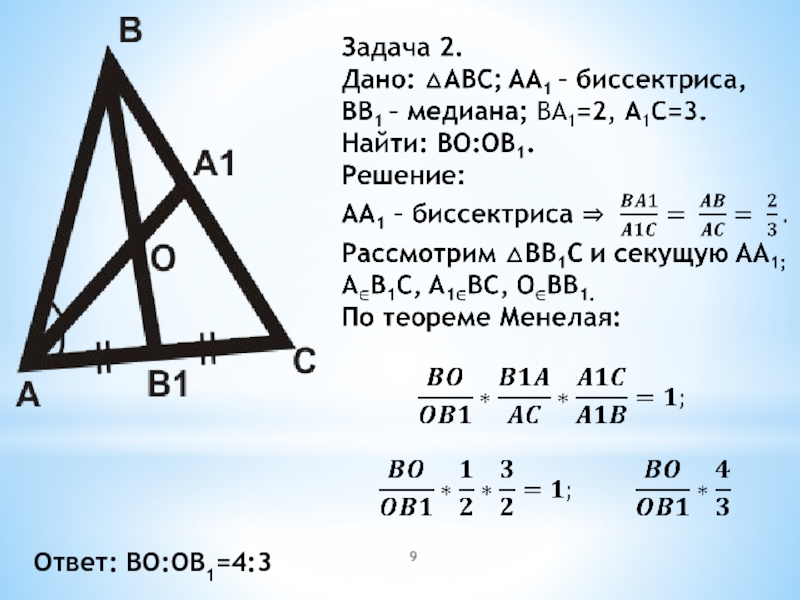
- 9. Ответ: BO:OB1=4:3
- 10. Задача 3.В треугольнике ABC точка D делит
- 11. Слайд 11
- 12. Слайд 12
- 13. Одним из замечательных свойств геометрических задач является
- 14. Спасибо за внимание!
• Исследовательская работа «Теорема Менелая» посвящена одной из самых трудных, но в то же время интересных и увлекательных тем геометрии - отношению отрезков. • Понятие пропорциональных отрезков используется при решении треугольников с применением теоремы Фалеса,
Слайд 2• Исследовательская работа «Теорема Менелая» посвящена одной из самых трудных, но
в то же время интересных и увлекательных тем геометрии - отношению отрезков.
• Понятие пропорциональных отрезков используется при решении треугольников с применением теоремы Фалеса, теоремы о свойстве биссектрисы треугольника, признаков подобия. Пропорциональность и подобие рассматриваются в трапециях и правильных многоугольниках.
• Обилие различных видов геометрических задач и многообразие приёмов и методов их решения делают геометрию наиболее трудным разделом школьной математики.
Введение
Слайд 3• Гипотеза: знание особых свойств и подходов к решению задач на
пропорциональные отрезки – необходимое условие успешного решения сложных планиметрических задач.
• Цель работы: ознакомление с теоремой Менелая ; исследование способов доказательства теоремы; овладение приемами решений планиметрических задач с использованием теоремы Менелая;
• Задачи исследования: проверить эффективность и целесообразность применения теоремы при решении задач;
научиться применять теорему Менелая в задачах разной сложности;
сравнить задачи, решенные с использованием теоремы Менелая с задачами, решенными традиционным способом.
• Объект исследования: задачи на свойства пропорциональных отрезков.
• Предмет исследования: методы решения задач.
О работе
Слайд 4Менелай Александрийский (1 век н.э.) написал «Сферику» в трех книгах. В
первой книге он представил основы для сферических треугольников. Вторая книга применяет сферическую геометрию к астрономии. Третья книга содержит «теорему Менелая», известную также как «правило шести величин».
Слайд 5Теорема:
Если △ ABC пересечен прямой, образующей точки M и N на
его сторонах AB и BC и точка K на продолжении стороны AC, то будет верно равенство:
Слайд 6Доказательство:
Проведем прямую M, непараллельную прямой MN. Проведем через вершины CABC прямые,
параллельные прямой MN, которые пересекаются с прямой M в точках B1, A1, C1.
Слайд 8По условию задачи MA=AC, NC=3BN.
Пусть MA=AC=b, BN=k, NC=3k.
Прямая MN пересекает две
стороны треугольника ABC и продолжение третьей.
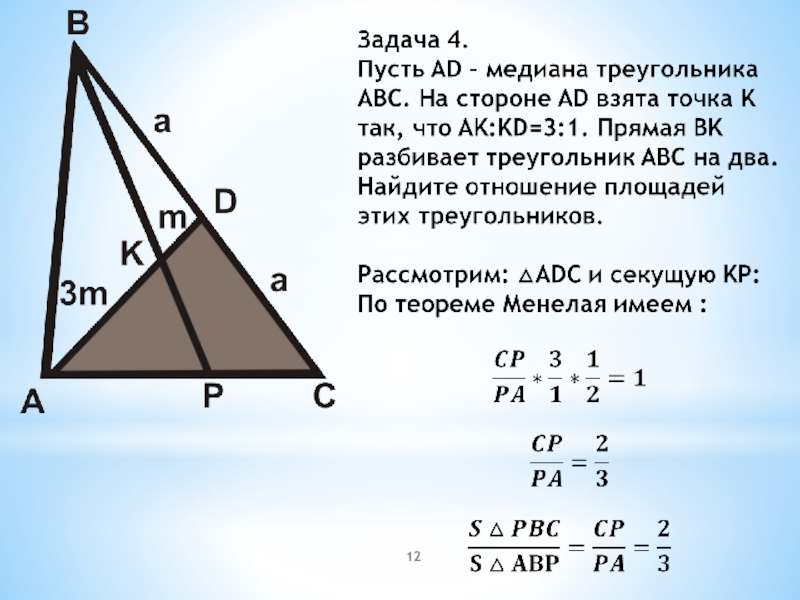
По теореме Менелая:
По теореме Менелая:
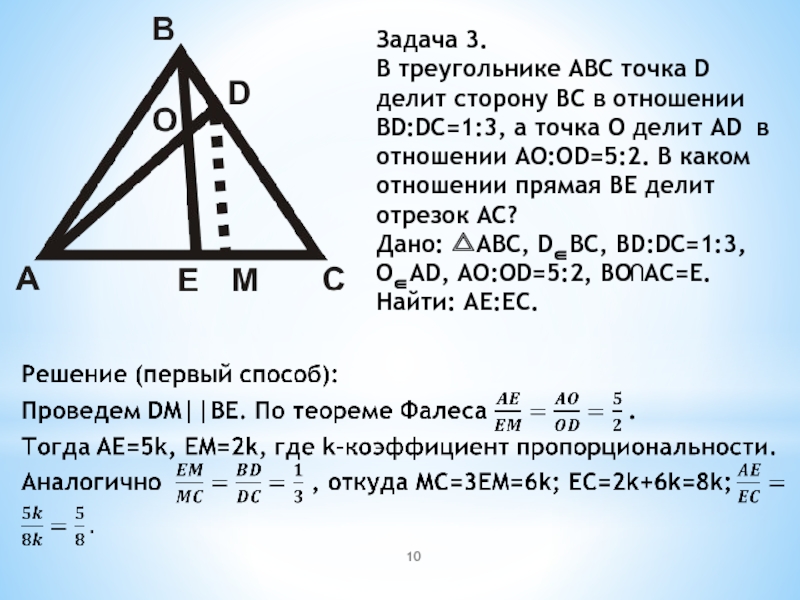
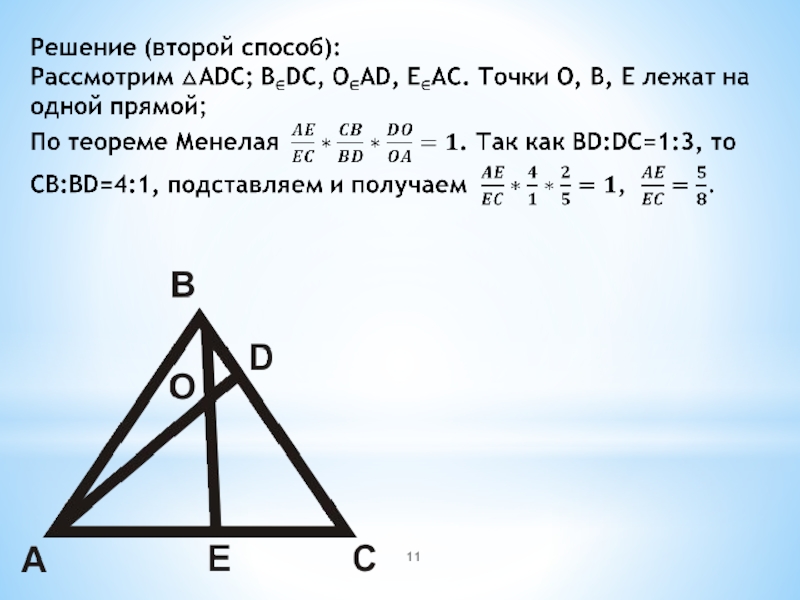
Слайд 10Задача 3.
В треугольнике ABC точка D делит сторону BC в отношении
BD:DC=1:3, а точка O делит AD в отношении AO:OD=5:2. В каком отношении прямая BE делит отрезок AC?
Дано: △ABC, D∈BC, BD:DC=1:3, O∈AD, AO:OD=5:2, BO⋂AC=E. Найти: AE:EC.
Дано: △ABC, D∈BC, BD:DC=1:3, O∈AD, AO:OD=5:2, BO⋂AC=E. Найти: AE:EC.
Слайд 13Одним из замечательных свойств геометрических задач является многообразие методов их решения.
Поэтому остановимся на том, когда же имеет смысл применять теорему Менелая при решении задач? Возможность применить теоремы Менелая имеет смысл, когда в условии задачи:
•идёт речь, об отношении отрезков (иногда завуалированном: доказать равенство отрезков, доказать, что точка является серединой отрезка);
•если на чертеже имеются элементы, присутствующие в теореме Менелая (треугольник и прямая, пересекающая его стороны или их продолжения);
•иногда полезно применять обратную теорему (если необходимо доказать, что какие-нибудь точки лежат на одной прямой). А также при доказательстве теорем.
Применение опыта решения планиметрических задач с использованием теоремы Менелая даёт дополнительные возможности при изучении геометрии, помогает повысить уровень пространственного воображения и уровень логической культуры.
Теорема Менелая помогает решить задачи более рационально, чем их решение другими способами; быстро и оригинально решить задачи повышенной сложности.
Эта теорема позволяют легко и изящно получить решение, в то время когда традиционные подходы приводят к громоздким и утомительным преобразованиям.
•идёт речь, об отношении отрезков (иногда завуалированном: доказать равенство отрезков, доказать, что точка является серединой отрезка);
•если на чертеже имеются элементы, присутствующие в теореме Менелая (треугольник и прямая, пересекающая его стороны или их продолжения);
•иногда полезно применять обратную теорему (если необходимо доказать, что какие-нибудь точки лежат на одной прямой). А также при доказательстве теорем.
Применение опыта решения планиметрических задач с использованием теоремы Менелая даёт дополнительные возможности при изучении геометрии, помогает повысить уровень пространственного воображения и уровень логической культуры.
Теорема Менелая помогает решить задачи более рационально, чем их решение другими способами; быстро и оригинально решить задачи повышенной сложности.
Эта теорема позволяют легко и изящно получить решение, в то время когда традиционные подходы приводят к громоздким и утомительным преобразованиям.
Заключение