- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Теорема Пифагора (8 класс)
Содержание
- 1. Презентация по математике на тему Теорема Пифагора (8 класс)
- 2. ЦЕЛИ: Познакомить с историей теоремы.Научить доказывать теорему.Показать
- 3. 1. Подготовительный этап(задачи на повторение)2. Историческая справка3. Теорема ПифагораПифагоровы тройки4. Применение теоремы5. Задачи6. «Золотые стихи» ПифагораСОДЕРЖАНИЕ
- 4. «…Геометрия владеет двумя сокровищами: Одно из них-
- 5. 1.Найдите площадь квадрата со стороной3 см; 1,2
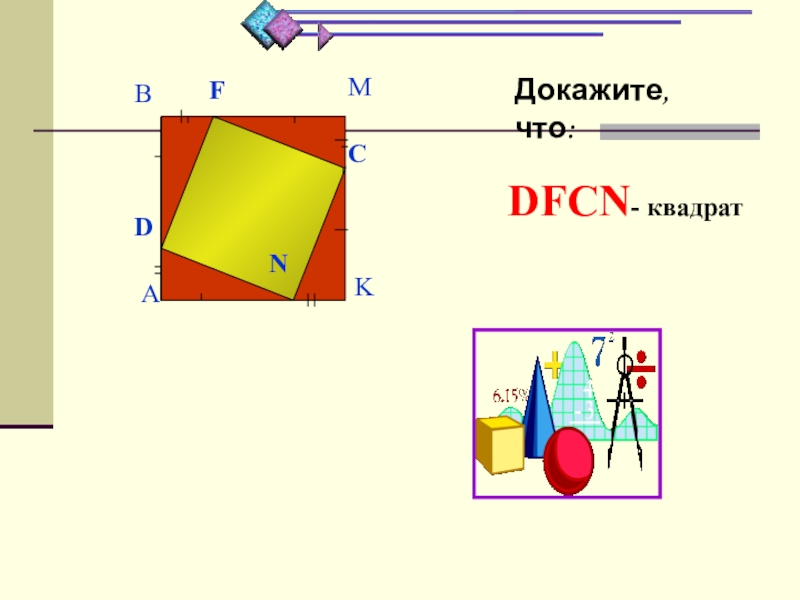
- 6. Докажите,что:DFCN- квадрат4.DFCNABMK
- 7. Знаменитый древнегреческий философ и математик Пифагор Самосский
- 8. Здесь в Кретоне, рождается школа Пифагора. В
- 9. делать то, что впоследствии не огорчит тебя
- 10. Пребудет вечной истина, как скороЕё познает слабый
- 11. Слайд 11
- 12. Теорема Пифагора в ЕгиптеЗа 2000 лет до
- 13. Теорема Пифагора в КитаеВ Древнем Китае за
- 14. Различные способы доказательства теоремы Пифагора.Доказательство, предложенное индусским
- 15. aaaaaaaabbbbbbbbСмотри!Среди пифагорейцев был распространён способ доказательства теоремы
- 16. Пифагоровы штаны во все стороны равны.
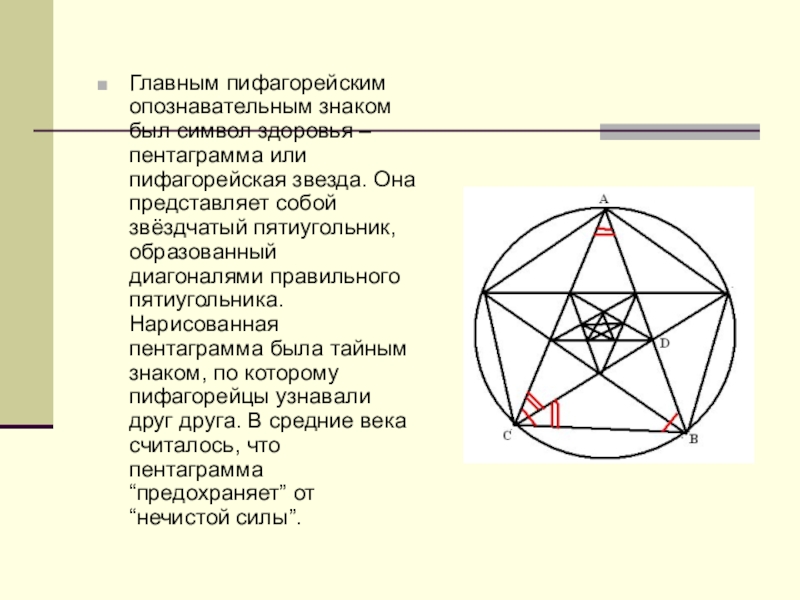
- 17. Главным пифагорейским опознавательным знаком был символ здоровья
- 18. Слайд 18
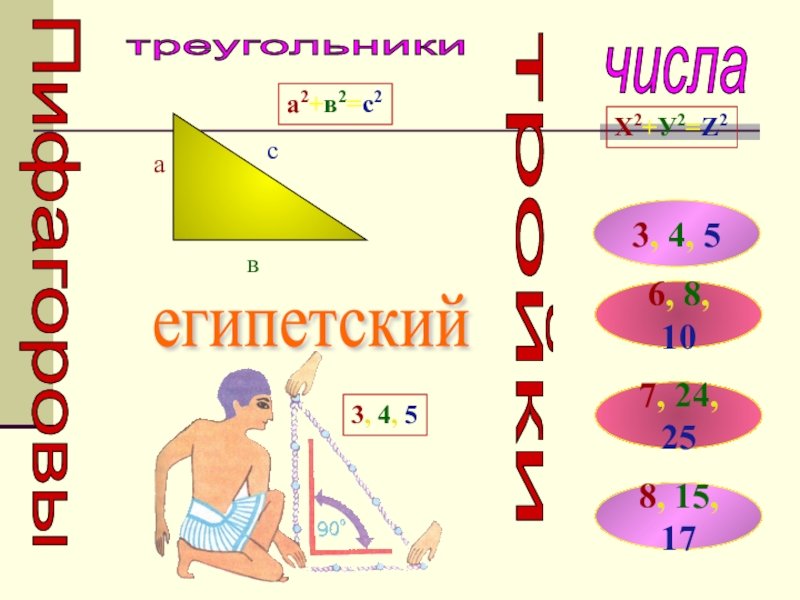
- 19. ПифагоровытройкичислатреугольникиХ2+У2=Z23, 4, 56, 8, 107, 24, 258, 15, 17асва2+в2=с2египетский3, 4, 5
- 20. abcabcabcabcВ прямоугольном треугольникеквадрат гипотенузы равенсумме квадратов катетов .а2+в2=с2Доказательство:S =(а+в)2S=c2+4·1/2ab(а+в)2=с2+4·1/2ава2+2ав+в2=с2+2ава2+в2=с2Теорема Пифагора
- 21. Слайд 21
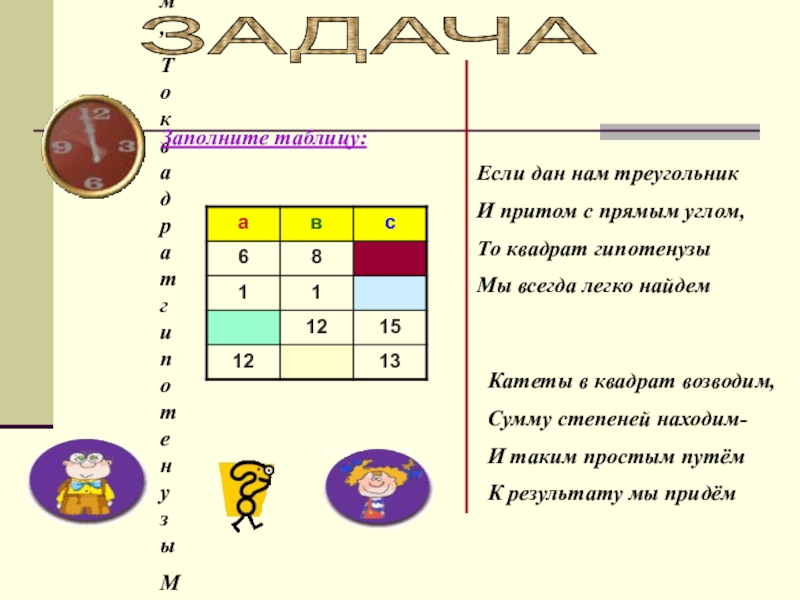
- 22. Если дан нам треугольникИ притом с прямым
- 23. Делай лишь
- 24. «Золотые стихи» ПифагораНе делай никогда того, что
- 25. «Золотые стихи» ПифагораНе закрывай глаз, когда хочется спать, не разобравши всех своих поступков в прошлый день.
- 26. Не пренебрегай здоровьем своего тела. Доставляй ему
- 27. это интересно«…что Иисус и Пифагор были уроженцами
- 28. ИТАК…Теорема Пифагора издавна широко применялась в разных
- 29. Домашнее задание:П.54, вопрос 8. Решить задачи №483 (в, г), №484 (в, г)
Слайд 1Презентация урока геометрии в 8 классе
по теме:”Теорема Пифагора”
Учитель математики Карцева Александра
МБОУ «Золотухинская средняя общеобразовательная школа»
Слайд 2ЦЕЛИ:
Познакомить с историей теоремы.
Научить доказывать теорему.
Показать применение теоремы.
Учить использовать полученные знания
Слайд 31. Подготовительный этап
(задачи на повторение)
2. Историческая справка
3. Теорема Пифагора
Пифагоровы тройки
4. Применение
5. Задачи
6. «Золотые стихи» Пифагора
СОДЕРЖАНИЕ
Слайд 4«…Геометрия владеет двумя сокровищами:
Одно из них- это теорема Пифагора,
Крайнем отношении…
Первое можно сравнить с мерой золота,
второе больше напоминает драгоценный камень.»
Иоганн Кеплер.
теорема
ПИФАГОРА
Слайд 5
1.Найдите площадь квадрата со стороной
3 см; 1,2 мм; 5\7 м;
Ответы: 9 см2; 1,44 см2; 25\49 см2; а2 см2.
2. Найдите площадь прямоугольного
треугольника с катетами 3 см и 4 см;
2,2 м и 5 см; а см и в см.
Ответы: 6 см2; 550 см2; 1\2 ав см2.
3. Чему равна площадь домика?
S
= 5 см2; S
=20 см2.
Ответ: 30 см2
Задачи на повторение
Слайд 7Знаменитый древнегреческий философ и математик Пифагор Самосский родился на острове Самос,
году до н. э. По античным свидетельствам он был красив и обладал незаурядными способностями. Совсем юношей он покинул родину, прошел по дорогам Египта и 12 лет жил в Вавилоне. После возвращения домой Пифагор переселился в Италию, затем в Сицилию.
580-500 г. до н. э.
Из жизни Пифагора
Слайд 8Здесь в Кретоне, рождается школа Пифагора. В пифагорейской школе занимались изучением
много внимания уделяли музыке, живописи, физическому развитию, здоровью. Пифагор и его ученики были трудолюбивы и аскетичны.
Здесь в Кретоне, рождается школа Пифагора. В пифагорейской школе занимались изучением чисел и их свойств,
много внимания уделяли музыке, живописи, физическому развитию, здоровью. Пифагор и его ученики были трудолюбивы и аскетичны.
Из жизни Пифагора
Слайд 9
делать то, что впоследствии не огорчит тебя и не принудит раскаиваться
не делай никогда того, что не знаешь, но научись всему, что следует знать;
не пренебрегай здоровьем своего тела;
приучайся жить просто и без роскоши.
Заповеди
Слайд 10Пребудет вечной истина, как скоро
Её познает слабый человек !
И ныне теорема
Верна, как и в его далекий век.
Они не в силах свету помешать,
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, её почуя , вслед.
Из истории теоремы
Слайд 12Теорема Пифагора в Египте
За 2000 лет до н.э. древние египтяне знали
Слайд 13Теорема Пифагора в Китае
В Древнем Китае за 1100 лет до н.э.
Слайд 14Различные способы доказательства теоремы Пифагора.
Доказательство, предложенное индусским математиком Бхаскара (12 в.)
Дано: АВС – прямоугольный треугольник, АВ = c, АС = a, ВС = b.
Достроить треугольник до квадрата со стороной, равной c.
Доказать, что с 2 = а 2 + b 2.
Доказательство Мёльманна.
Дано: АВС – прямоугольный треугольник, описанный около окружности
с центром О. АВ = с, АС = b, ВС = а.
Доказать, что с 2 = а 2 + b 2 . ( r = ( a + b +c ) / 2
Доказательство Гарфилла.
Дано: АВС – прямоугольный треугольник, АВ = с, АС = b, BC = c.
Доказать, что c 2 = a 2 + b 2.
Слайд 15
a
a
a
a
a
a
a
a
b
b
b
b
b
b
b
b
Смотри!
Среди пифагорейцев был распространён способ доказательства теоремы “без слов”. Слушателям представляли
Слайд 17Главным пифагорейским опознавательным знаком был символ здоровья – пентаграмма или пифагорейская
Слайд 19Пифагоровы
тройки
числа
треугольники
Х2+У2=Z2
3, 4, 5
6, 8, 10
7, 24, 25
8, 15, 17
а
с
в
а2+в2=с2
египетский
3, 4, 5
Слайд 20
a
b
c
a
b
c
a
b
c
a
b
c
В прямоугольном треугольнике
квадрат гипотенузы равен
сумме квадратов катетов .
а2+в2=с2
Доказательство:
S
=(а+в)2
S
=c2+4·1/2ab
(а+в)2=с2+4·1/2ав
а2+2ав+в2=с2+2ав
а2+в2=с2
Теорема Пифагора
Слайд 22Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда
Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем
Катеты в квадрат возводим,
Сумму степеней находим-
И таким простым путём
К результату мы придём
Заполните таблицу:
ЗАДАЧА
Слайд 23
Делай лишь то.что в последствии
«Золотые стихи» Пифагора
Слайд 24«Золотые стихи» Пифагора
Не делай никогда того, что не знаешь, но научись
Слайд 25«Золотые стихи» Пифагора
Не закрывай глаз, когда хочется спать, не разобравши всех
Слайд 26Не пренебрегай здоровьем своего тела.
Доставляй ему вовремя пищу и питьё,
«Золотые стихи» Пифагора
Не пренебрегай здоровьем своего тела.
Доставляй ему вовремя пищу и питьё, и упражнения, в которых он нуждается.
Слайд 27это интересно
«…что Иисус и Пифагор были уроженцами почти одной и той
«…их отцы были пророчески извещены о том, что у них родятся сыновья, которые явятся благодетелями человечества…» «…что оба родились в то время, когда их родители были вне дома…»
Слайд 28ИТАК…
Теорема Пифагора издавна широко применялась в разных областях науки, техники и
Пребудет вечной истина, как скоро, Все познает слабый человек! И ныне теорема Пифагора Верна, как и в его далекий век. А.Шамиссо