- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Теорема Пифагора (8 класс)
Содержание
- 1. Презентация по математике на тему Теорема Пифагора (8 класс)
- 2. Содержание:Кто такой Пифагор Самосский?Теорема Пифагора, её доказательство.Решение задачи.Практическое применение теоремы.
- 3. «Геометрия владеет двумя сокровищами: одно из
- 4. Пифагор Самосский(ок. 580 – ок. 500 г. до н.э.)
- 5. О ПифагореПифагор Самосский родился на острове Самосс
- 6. Трудно найти человека, который не знал бы
- 7. Теорема ПифагораВ прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетовсавс² = а² + в² гипотенузакатеты
- 8. Докажем теорему!Способ 1Дан треугольник AMK с катетами
- 9. Способ 2cДан треугольник ABC c катетами a
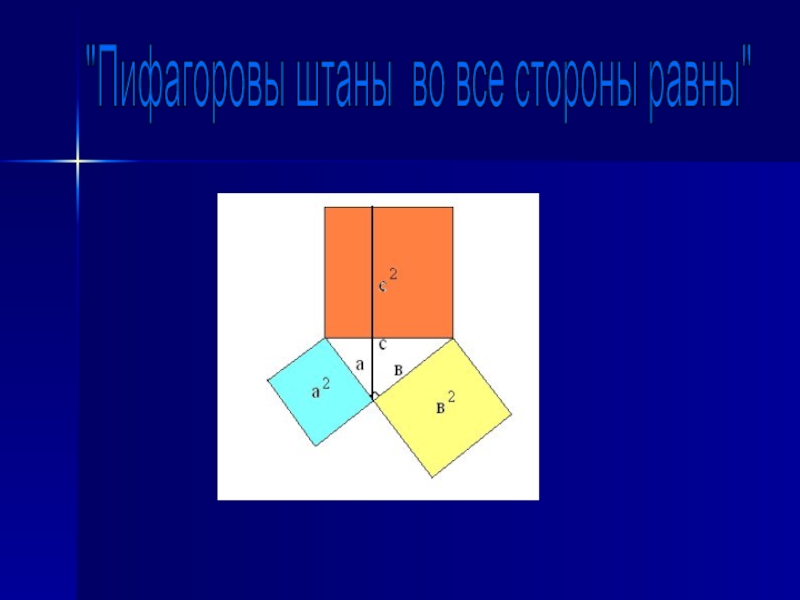
- 10. "Пифагоровы штаны во все стороны равны"
- 11. Решение старинных задач Теорема Пифагора всегда имела широкое
- 12. Задача из учебника «Арифметика»
- 13. В древней Индии был обычай предлагать задачи
- 14. Решение геометрических задачx43xx32x55Х² = 3² + 4²Х
- 15. ОБЛАСТИ ПРИМЕНЕНИЯАрхитектура и строительствоМобильная связьАстрономия
- 16. АрхитектураВ зданиях готического и романского стиля верхние
- 17. В романской архитектуре часто встречается мотив, представленный
- 18. СтроительствоПри строительстве любого сооружения, рассчитывают расстояния, центры тяжести, размещение опор, балок и т.д.
- 19. Строительство крыши При строительстве домов и коттеджей часто
- 20. Молниеотвод Известно, что молниеотвод защищает от
- 21. Мобильная связь Какую наибольшую высоту должна
- 22. Астрономия В конце девятнадцатого века высказывались
- 23. Пифагор- это не только великий математик, но и великий мыслитель своего времени.
- 24. Значение теоремы ПифагораЗначение теоремы Пифагора состоит в
- 25. В Германии недавно открылся кинотеатр,
- 26. В целом, значение теоремы, кроме вышесказанного, заключается
Слайд 2Содержание:
Кто такой Пифагор Самосский?
Теорема Пифагора, её доказательство.
Решение задачи.
Практическое применение теоремы.
Слайд 5О Пифагоре
Пифагор Самосский родился на острове Самосс в Ионическом море.
Пифагор был
Он принимал в свою школу только тех юношей, которые промолчали в течение пяти лет. Значит, при занятиях математикой нужна абсолютная тишина для того, чтобы можно было сосредоточить все внимание на решении того или другого утверждения.
Слайд 6Трудно найти человека, который не знал бы её шуточную формулировку: «Пифагоровы
Сегодня известно около 500 различных доказательств теоремы Пифагора геометрических, алгебраических, механических и прочих.
Слайд 7Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
с
а
в
с² =
гипотенуза
катеты
Слайд 8Докажем теорему!
Способ 1
Дан треугольник AMK с катетами a, b и гипотенузой
Достроим к треугольнику AMK квадрат со стороной a+b.
S кв = (a+b)²
Треугольники равны
Четырёхугольник KMNP – квадрат, т.к.<1=<2=<3=<4 и <5=<6=<7=<8 => <1+<8 = <2+<5 = <3+<6 = <4+<7 =90°.
Найдём площадь квадрата ABCD
S кв =4Sтр + S1кв =4x ½ ab + c² = 2ab +c²
Тогда (a+b)² = 2ab+c²
a² + 2ab + b² = 2ab +c² , a² + b² = c².
1
2
3
4
5
6
7
8
а
в
а
в
а
в
N
P
Слайд 9Способ 2
c
Дан треугольник ABC c катетами a и b.
Продолжим отрезок СВ
Точки А и М соединим отрезком АМ.
AMDC – прямоугольная трапеция.
В прямоугольных треугольниках ABC и BMD <1 + <2 =90° и <3+<4=90°, но так как <1 = <3, то <3 + <2 = 90°; тогда SABC + S ABM + S BMD = Sтрап , или Умножив обе части равенства на 2, получим 1 2 3 4
½ ab + ½ с²+ ½ ab = ½(a+b)(a+b).
ab + c² + ab = (a + b)², 2ab + c²= a² + 2ab + b², откуда c²= a² + b².
Слайд 11Решение старинных задач
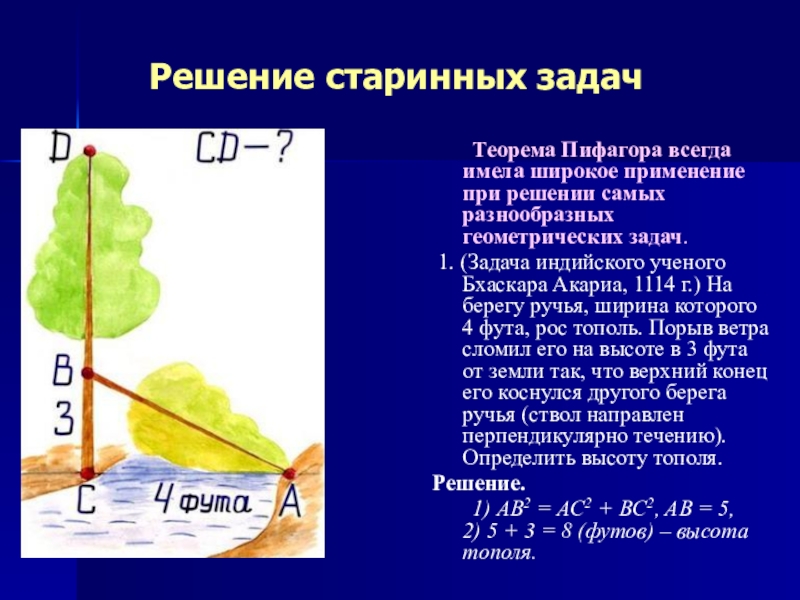
Теорема Пифагора всегда имела широкое применение при решении самых
1. (Задача индийского ученого Бхаскара Акариа, 1114 г.) На берегу ручья, ширина которого 4 фута, рос тополь. Порыв ветра сломил его на высоте в 3 фута от земли так, что верхний конец его коснулся другого берега ручья (ствол направлен перпендикулярно течению). Определить высоту тополя.
Решение.
1) AB2 = AC2 + BC2, AB = 5, 2) 5 + 3 = 8 (футов) – высота тополя.
Слайд 12Задача из учебника «Арифметика»
«Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать».
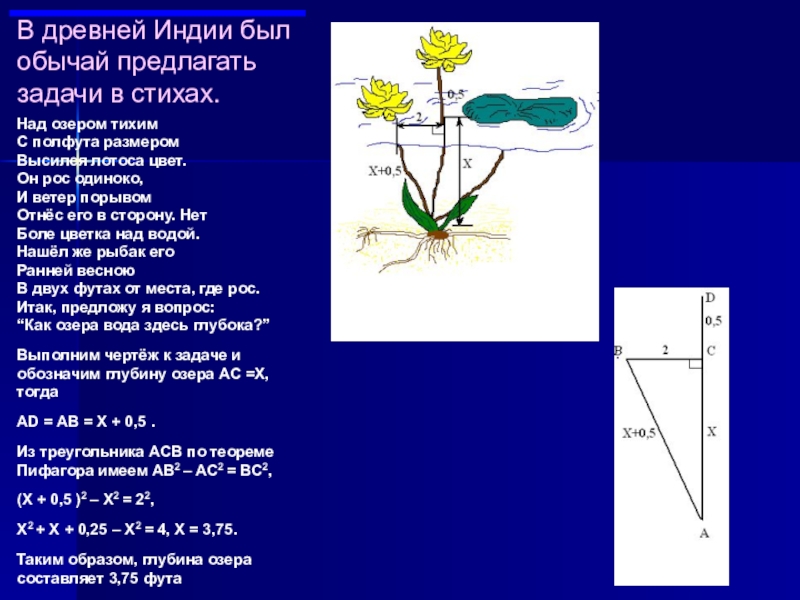
Слайд 13В древней Индии был обычай предлагать задачи в стихах.
Над озером тихим
С
Выполним чертёж к задаче и обозначим глубину озера АС =Х, тогда
AD = AB = Х + 0,5 .
Из треугольника ACB по теореме Пифагора имеем AB2 – AC2 = BC2,
(Х + 0,5 )2 – Х2 = 22,
Х2 + Х + 0,25 – Х2 = 4, Х = 3,75.
Таким образом, глубина озера составляет 3,75 фута
Слайд 14Решение геометрических задач
x
4
3
x
x
32
x
5
5
Х² = 3² + 4²
Х = 5
Х² + Х²
Х = 16√2
х² = 5²+ 5²
х =5√2
Слайд 16Архитектура
В зданиях готического и романского стиля верхние части окон расчленяются каменными
ширине окна (b) для наружных дуг
половине ширины, (b/2) для внутренних дуг
Остается еще полная окружность, касающаяся четырех дуг. Т. к. она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между
этими окружностями, т. е. b/2 и, следовательно,
радиус равен b/4. А тогда становится ясным и
положение ее центра.
Слайд 17В романской архитектуре часто встречается мотив, представленный на рисунке. Если b
(b/4+p)=( b/4)+( b/4-p)
или
b/16+ bp/2+p=b/16+b/4-bp+p,
откуда
bp/2=b/4-bp.
Разделив на b и приводя подобные члены, получим:
(3/2)p=b/4, p=b/6.
Слайд 18Строительство
При строительстве любого сооружения, рассчитывают расстояния, центры тяжести, размещение опор, балок
Слайд 19Строительство крыши
При строительстве домов и коттеджей часто встает вопрос о длине
Решение:
Треугольник ADC - равнобедренный AB=BC=4 м., BF=4 м. Если предположить, что FD=1,5 м., тогда:
А) Из треугольника DBC: DB=2,5 м.,
Б) Из треугольника ABF:
Слайд 20Молниеотвод
Известно, что молниеотвод защищает от молнии все предметы, расстояние
Решение:
По теореме Пифагора h2≥ a2+b2, значит h≥(a2+b2)1/2.
Слайд 21Мобильная связь
Какую наибольшую высоту должна иметь антенна мобильного оператора,
Решение:
Пусть AB= x, BC=R=200 км, OC= r =6380 км.
OB=OA+AB OB=r + x.
Используя теорему Пифагора, получим
Ответ: 2,3 км.
Слайд 22Астрономия
В конце девятнадцатого века высказывались разнообразные предположения о существовании
Слайд 24Значение теоремы Пифагора
Значение теоремы Пифагора состоит в том, что из нее
Кроме этого, практическое значение теоремы Пифагора и обратной ему теоремы заключается в том, что с их помощью можно найти длины отрезков, не измеряя самих отрезков.