- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Теорема Пифагора (8 класс)
Содержание
- 1. Презентация по математике на тему Теорема Пифагора (8 класс)
- 2. История открытия теоремы
- 3. История открытия теоремы Крупнейший немецкий
- 4. Значение теоремы «Геометрия владеет двумя сокровищами: одно
- 5. Значение теоремы Теорема Пифагора
- 6. Теорема о квадрате диагонали прямоугольного параллелепипеда —
- 7. Некоторые способы доказательства теоремы Пифагора
- 8. Простейшее доказательствоАВС Вероятно, факт, изложенный в
- 9. Доказательство, основанное на равновеликости фигураbcbabaabccc
- 10. Алгебраический метод доказательстваЭтот рисунок — иллюстрацию доказательства
- 11. Доказательство методом достроенияАВСЕFDPQMNЭтот способ доказательства предложил великий
- 12. Доказательство Гарфилда132baccabТри прямоугольных треугольника 1, 2 и
- 13. Пифагоровы штаны (доказательство Евклида) В
- 14. Устами Пифагора Нравственные принципы и
- 15. Слайд 15
Слайд 1Теорема Пифагора:
простота, красота, значимость.
Презентация к уроку
по теме «Теорема Пифагора»
8
Учитель математики
МКОУ Назаровская ООШ
Галкина Ирина Петровна.
Слайд 2История открытия теоремы
Обычно открытие знаменитой теоремы
Так, например, в древнекитайской математической книге Чу-пей так говорится о прямоугольном треугольнике со сторонами 3, 4 и 5: «Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4». Теорема Пифагора была обнаружена и в другом древнекитайском трактате, время создания которого точно неизвестно, но где утверждается, что в XV в. до н. э. китайцы знали свойства египетского треугольника и общий вид теоремы.
Слайд 3История открытия теоремы
Крупнейший немецкий историк математики Кантор считает,
32 + 42 = 52 было известно египтянам ещё около 2300 г. до н. э. известны египетские рисунки, на которых изображены плотники, пользующиеся треугольником со сторонами 3, 4 и 5.
В Вавилоне ещё в 2000 г. до н. э. умели вычислять гипотенузу прямоугольного треугольника.
У древних индусов геометрия была тесно связана с культом, и о теореме о квадрате гипотенузы было известно ещё в XVIII в. до н. э.
Но несмотря на все эти факты имя Пифагора так прочно срослось с теоремой Пифагора, что просто невозможно представить себе, что это словосочетание распадётся.
Слайд 4Значение теоремы
«Геометрия владеет двумя сокровищами:
одно из них – теорема
Иоганн Кеплер.
Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с его теоремой. Даже те, кто навсегда распрощался с математикой, знают, что «Пифагоровы штаны во все стороны равны». Существуют и стихотворные формулировки знаменитой теоремы:
Если дан нам треугольник Катеты в квадрат возводим,
И при том с прямым углом, Сумму степеней находим –
То квадрат гипотенузы И таким простым путём
Мы всегда легко найдём: К результату мы придём.
Теорема Пифагора — одна из важнейших теорем геометрии, и тот факт, что существует более 500 различных доказательств этой теоремы, свидетельствует о гигантском числе её конкретных реализаций.
Слайд 5Значение теоремы
Теорема Пифагора была первым утверждением, связавшим
Благодаря тому, что теорема Пифагора позволяет находить длину отрезка, не измеряя его непосредственно, она как бы открывает путь с прямой на плоскость, с плоскости в пространство.
В 10 классе изучается теорема о квадрате диагонали прямоугольного параллелепипеда, которую можно считать обобщением теоремы Пифагора.
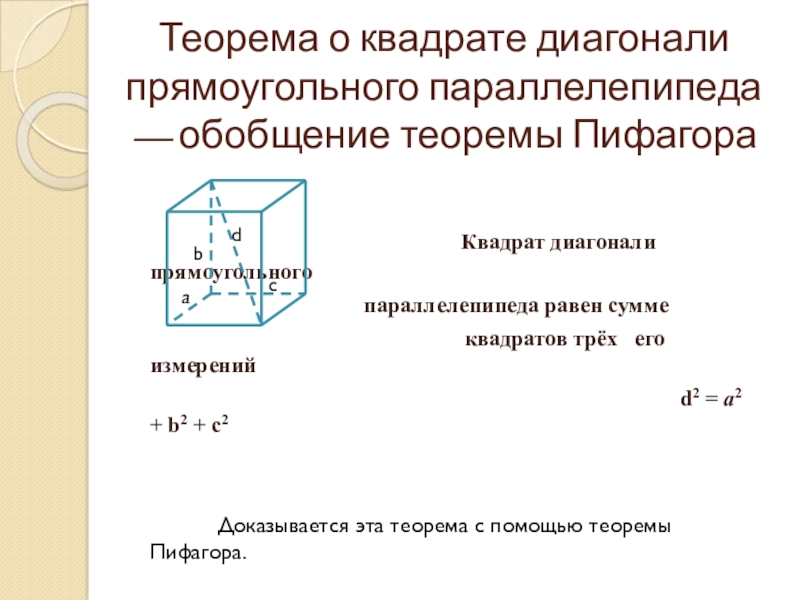
Слайд 6Теорема о квадрате диагонали прямоугольного параллелепипеда — обобщение теоремы Пифагора
параллелепипеда равен сумме
квадратов трёх его измерений
d2 = a2 + b2 + c2
Доказывается эта теорема с помощью теоремы Пифагора.
d
a
b
c
Слайд 8Простейшее доказательство
А
В
С
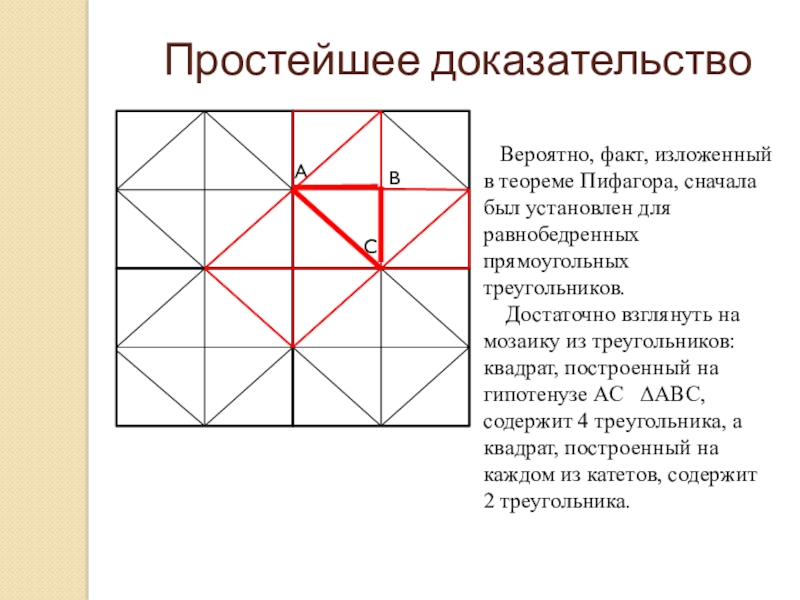
Вероятно, факт, изложенный в теореме Пифагора, сначала был
Достаточно взглянуть на мозаику из треугольников: квадрат, построенный на гипотенузе АС АВС, содержит 4 треугольника, а квадрат, построенный на каждом из катетов, содержит
2 треугольника.
Слайд 9Доказательство,
основанное на равновеликости фигур
а
b
c
b
a
b
a
a
b
c
c
c
Квадрат, длина стороны которого
a
квадрат и 4 равных прямоугольных треугольника.
Площадь внешнего квадрата
S = (a + b)2
Площадь внутреннего квадрата
Площадь одного треугольника
Тогда площадь внутреннего квадрата равна разности площадей внешнего квадрата и четырёх треугольников:
S = c2
S =
c2 = (a + b)2 4·
c2 = a2 + 2ab +b2 – 2
c2 = a2 + b2
Древние индусы, которым принадлежало это рассуждение, не записывали его, а сопровождали чертёж только одним словом: «СМОТРИ!»
Слайд 10Алгебраический метод доказательства
Этот рисунок — иллюстрацию доказательства великого индийского математика Бхаскары,
b
a
c
(b – a)2
На гипотенузе прямоугольного треугольника Бхаскара строил квадрат, площадь которого он находил как сумму площадей четырёх равных прямоугольных треугольников и малого квадрата.
- площадь одного треугольника.
Площадь большого квадрата S = c2
S =
Площадь малого квадрата: S = (b – a)2
c2 = 4· + (b – a)2 = 2аb+
b2 – 2ab+a2 =
a2 + b2
Слайд 11Доказательство методом достроения
А
В
С
Е
F
D
P
Q
M
N
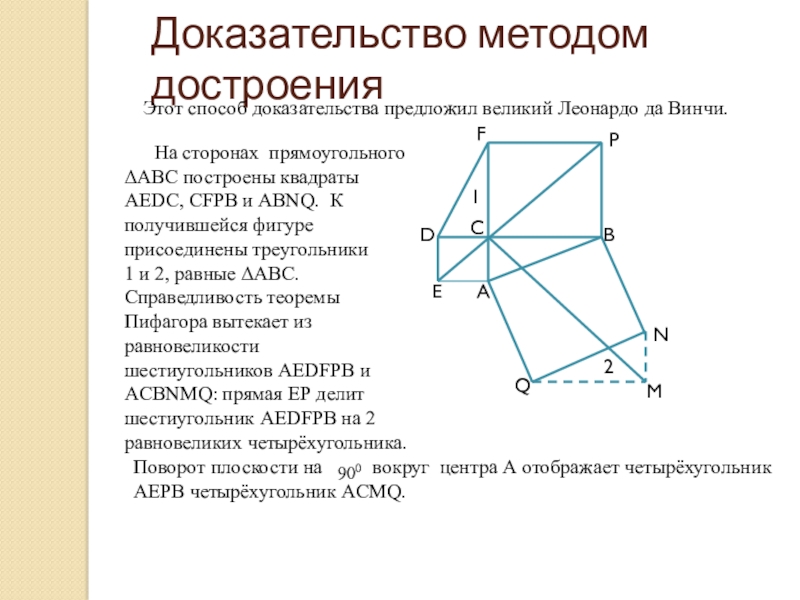
Этот способ доказательства предложил великий Леонардо да Винчи.
1
2
1 и 2, равные АВС.
Справедливость теоремы Пифагора вытекает из равновеликости шестиугольников AEDFPB и ACBNMQ: прямая ЕР делит шестиугольник AEDFPB на 2 равновеликих четырёхугольника.
900
Поворот плоскости на вокруг центра А отображает четырёхугольник АЕРВ четырёхугольник ACMQ.
Слайд 12Доказательство Гарфилда
1
3
2
b
a
c
c
a
b
Три прямоугольных треугольника 1, 2 и 3 составляют трапецию, площадь
Площадь трапеции равна сумме площадей треугольников, из которых она состоит:
Приравнивая эти выражения, получим теорему Пифагора:
c2 = a2 + b2
Слайд 13Пифагоровы штаны
(доказательство Евклида)
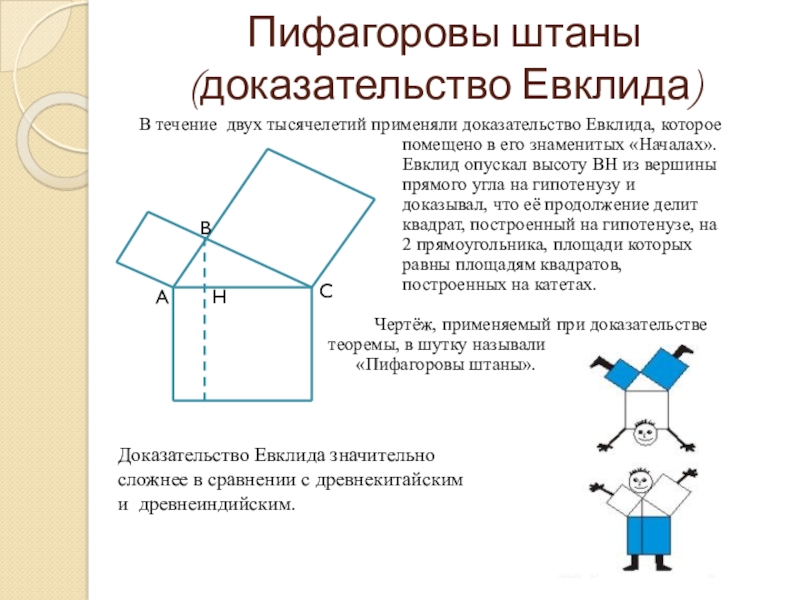
В течение двух тысячелетий применяли доказательство
помещено в его знаменитых «Началах».
Евклид опускал высоту ВН из вершины
прямого угла на гипотенузу и
доказывал, что её продолжение делит
квадрат, построенный на гипотенузе, на
2 прямоугольника, площади которых
равны площадям квадратов,
построенных на катетах.
Чертёж, применяемый при доказательстве
теоремы, в шутку называли
«Пифагоровы штаны».
Н
В
А
С
Доказательство Евклида значительно сложнее в сравнении с древнекитайским
и древнеиндийским.
Слайд 14Устами Пифагора
Нравственные принципы и правила, проповедуемые Пифагором, и
Беги от всякой хитрости; отсекай огнём, железом и любым оружием от тела болезнь, от души – невежество, от утробы – роскошь, от города – смуту, от семьи – ссору.
Будь справедлив и в словах, и в поступках своих…
Делай великое, не обещая великого.
Одному только разуму, как мудрому попечителю, должно вверять свою жизнь.
Статую красит вид, а человека – деяние его.
Пьянство есть упражнение в безумии.
Живи с людьми так, чтобы друзья не стали недругами, а недруги стали друзьями.
Только неблагородный человек способен в глаза хвалить, а за глаза злословить.