- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему: Сумма углов треугольника
Содержание
- 1. Презентация по математике на тему: Сумма углов треугольника
- 2. Тема урока: ТЕОРЕМА О СУММЕ УГЛОВ ТРЕУГОЛЬНИКА.
- 3. ЦЕЛЬ: Сформировать и доказать теоремы о сумме
- 4. Часто знает и дошкольник,Что такое треугольник.А уж
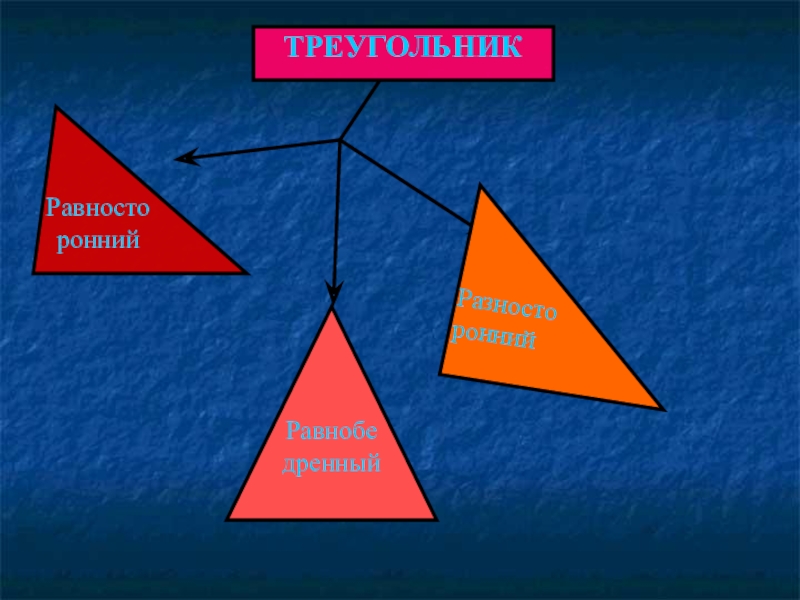
- 5. ТРЕУГОЛЬНИКРавностороннийРавнобедренныйРазносторонний
- 6. «УГОЛ» 1. Угол – это фигура…..... 2.
- 7. Угол – это фигура, образованная двумя лучами,
- 8. Внутренний угол треугольника – угол, образованный его
- 9. ТРЕУГОЛЬНИКТупоугольныйОстроугольныйПрямоугольный
- 10. Теорема: СУММА УГЛОВ ТРЕУГОЛЬНИКА РАВНА 180.ДАНО: ∆
- 11. ДОКАЗАТЕЛЬСТВО:1.ПРОВЕДЕМ а ‖ ВС, А
- 12. Физкультминутка.Встать из-за парты и показать руками:развернутый угол,прямой угол;тупой угол;острый угол;параллельные прямые.
- 13. 1) Что такое внешний угол треугольника? 2) Чему равна величина внешнего угла треугольника?
- 14. Ответы.Внешним углом треугольника называют угол, смежный с
- 15. ДАНО: ∆ АВС, ∠ 4 – внешний
- 16. ДОКАЗАТЕЛЬСТВО:1. ПО СВОЙСТВУ СМЕЖНЫХ УГЛОВ ∠
- 17. 1) Что утверждает новая теорема?2) Чему равен
- 18. Ответы.Сумма трёх углов любого треугольника равна 180°.100°
- 19. 3) Чему равен угол равностороннего треугольника?
- 20. Ответ на вопрос №3Все три угла равны
- 21. 4) Чему равна сумма острых углов прямоугольного треугольника? 12
- 22. Ответ на вопрос №4180° – 90° = 90° 90° составляет сумма острых углов прямоугольного треугольника.
- 23. 5) Чему равен острый угол прямоугольного равнобедренного треугольника? ==
- 24. Ответ на вопрос №545 , т.к. вместе
- 25. САМОСТОЯТЕЛЬНАЯ РАБОТАРешите из учебника задание №223 а) с.70
- 26. САМОПРОВЕРКАРешение:∠ А + ∠ В + ∠
- 27. ДОМАШНЕЕ ЗАДАНИЕ: п. 31 № 223(б), № 226 , 234*
Тема урока: ТЕОРЕМА О СУММЕ УГЛОВ ТРЕУГОЛЬНИКА.
Слайд 1Горловкий лицей №85
«Гармония»
учитель математики
Лазуткина И.П.
Разработка урока по геометрии
7 класс
Слайд 3ЦЕЛЬ: Сформировать и доказать теоремы о сумме углов треугольника и о
величине внешнего угла треугольника; формировать умения анализировать, обобщать; научить решать задачи на применение теорем, развивать и тренировать геометрическое зрение.
Слайд 4Часто знает и дошкольник,
Что такое треугольник.
А уж ВАМ – то как
не знать.
Но совсем другое дело –
Быстро, точно и умело
Треугольники считать.
Но совсем другое дело –
Быстро, точно и умело
Треугольники считать.
Слайд 6«УГОЛ»
1. Угол – это фигура….....
2. Если……., то угол называют……
3. Внутренний угол треугольника – это…..
Слайд 7Угол – это фигура, образованная двумя лучами, выходящими из одной точки.
Лучи называют сторонами угла, а точку – вершиной.
Если величина угла 90, то угол называют прямым, если 180, то развернутым. Угол, меньше 90 называют острым углом, больше 90, но меньше 180 – тупым. Таким образом, углы бывают тупые, острые, прямые, развёрнутые.
Если величина угла 90, то угол называют прямым, если 180, то развернутым. Угол, меньше 90 называют острым углом, больше 90, но меньше 180 – тупым. Таким образом, углы бывают тупые, острые, прямые, развёрнутые.
Слайд 8Внутренний угол треугольника – угол, образованный его сторонами, вершина треугольника является
вершиной его угла. Значит, в треугольнике углы могут быть различными: тупыми, острыми, прямыми
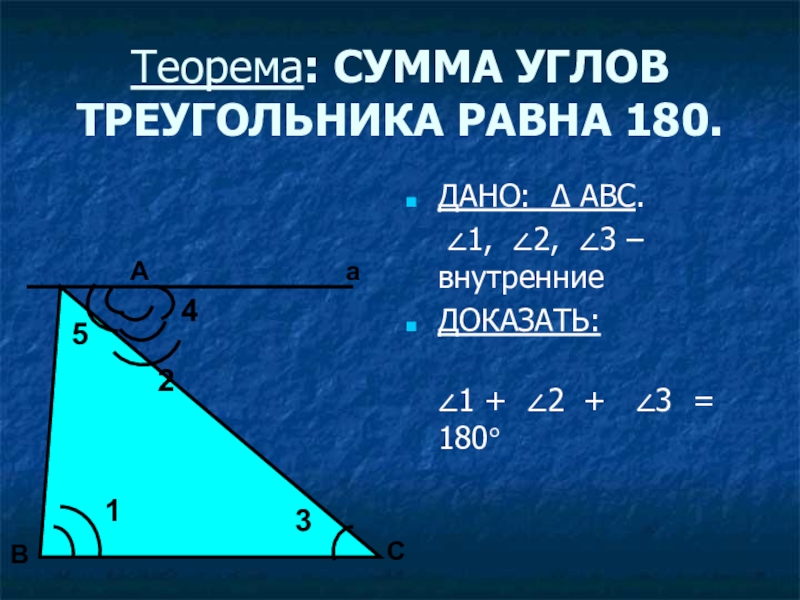
Слайд 10Теорема: СУММА УГЛОВ ТРЕУГОЛЬНИКА РАВНА 180.
ДАНО: ∆ АВС.
∠1, ∠2,
∠3 – внутренние
ДОКАЗАТЬ:
∠1 + ∠2 + ∠3 = 180°
ДОКАЗАТЬ:
∠1 + ∠2 + ∠3 = 180°
A
B
C
1
3
4
5
2
a
Слайд 11ДОКАЗАТЕЛЬСТВО:
1.ПРОВЕДЕМ а ‖ ВС, А є а
2. ∠5 =
∠1 (внутренние накрест лежащие при а ‖ ВС и АВ - секущей)
∠4 = ∠3 (внутренние накрест лежащие при а ‖ ВС и АС - секущей)
3. Представим развернутый угол в виде суммы
∠5 + ∠ 2 + ∠4 = 180 ° (развернутый угол)
4. Заменить слагаемые равными им углами треугольника
∠ 1 + ∠ 2 + ∠ 3 = 180 ° . ч. и т. д
∠4 = ∠3 (внутренние накрест лежащие при а ‖ ВС и АС - секущей)
3. Представим развернутый угол в виде суммы
∠5 + ∠ 2 + ∠4 = 180 ° (развернутый угол)
4. Заменить слагаемые равными им углами треугольника
∠ 1 + ∠ 2 + ∠ 3 = 180 ° . ч. и т. д
Слайд 12Физкультминутка.
Встать из-за парты и показать руками:
развернутый угол,
прямой угол;
тупой угол;
острый угол;
параллельные прямые.
Слайд 14Ответы.
Внешним углом треугольника называют угол, смежный с внутренним.
Внешний угол треугольника равен
сумме двух углов треугольника, не смежных с ним.
Слайд 16 ДОКАЗАТЕЛЬСТВО:
1. ПО СВОЙСТВУ СМЕЖНЫХ УГЛОВ
∠ 4 + ∠ 3
= 180° .
2. ПО ТЕОРЕМЕ О СУММЕ УГЛОВ ТРЕУГОЛЬНИКА
(∠ 1 + ∠ 2) + ∠ 3 = 180°
3. ∠ 4 = ∠ 1 + ∠ 2. ч. и т. д.
2. ПО ТЕОРЕМЕ О СУММЕ УГЛОВ ТРЕУГОЛЬНИКА
(∠ 1 + ∠ 2) + ∠ 3 = 180°
3. ∠ 4 = ∠ 1 + ∠ 2. ч. и т. д.
Слайд 171) Что утверждает новая теорема?
2) Чему равен третий угол в треугольнике,
если один из углов 30° , второй 100° ?
Слайд 18Ответы.
Сумма трёх углов любого треугольника равна 180°.
100° + 30° = 130°
180° – 130° = 50°
Третий угол равен 50°
Третий угол равен 50°
Слайд 20Ответ на вопрос №3
Все три угла равны =>
180° :
3 = 60°.
60° – величина каждого угла равностороннего треугольника.
60° – величина каждого угла равностороннего треугольника.
Слайд 22Ответ на вопрос №4
180° – 90° = 90°
90° составляет
сумма острых углов прямоугольного треугольника.
Слайд 24Ответ на вопрос №5
45 , т.к. вместе два угла составляют 90
(
180° – 90° = 90°; 90° : 2 = 45° )
Слайд 26САМОПРОВЕРКА
Решение:
∠ А + ∠ В + ∠ С = 180°
∠ С
=180° -(∠ А + ∠ В )
∠ С = 180° -(65°+57°)=58°
Ответ: ∠ С =58°
∠ С = 180° -(65°+57°)=58°
Ответ: ∠ С =58°