№12» г.Набережные Челны
Султангалиной Г.Г.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Справочник по геометрии (7 класс)
Содержание
- 1. Презентация по математике на тему Справочник по геометрии (7 класс)
- 2. отрезок1. Отрезок – часть прямой, ограниченная с
- 3. Стороны угла – лучи ВА и ВМ.
- 4. 4. Два дополнительных друг другу луча образуют развернутый угол.ОВАРазвернутый угол АОВ
- 5. Ф1Ф2Ф2Ф1 = Ф25. Две геометрические фигуры называются равными, если их можно совместить наложением.
- 6. АВТочка С – середина отрезка6. Точка отрезка, делящая его пополам, называется серединой отрезка.
- 7. ВМА АВО = ОВМOЛуч ВО –
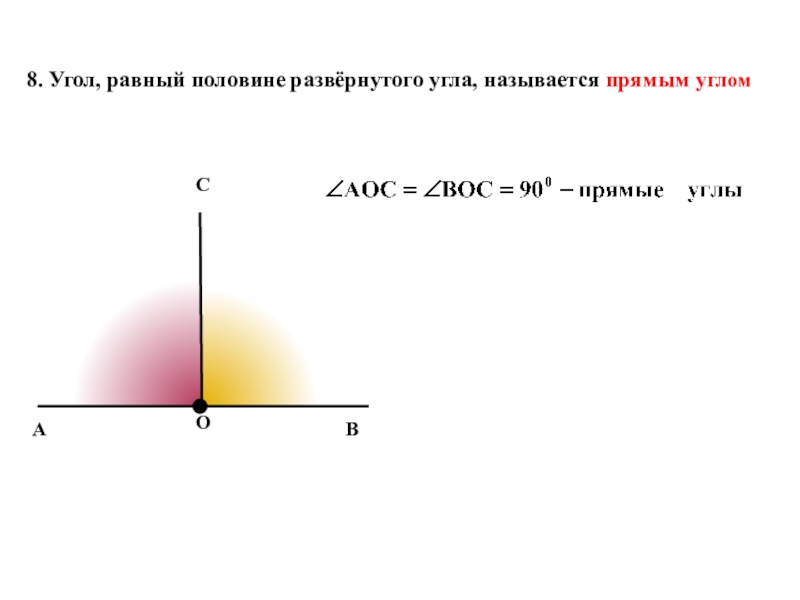
- 8. АВОС8. Угол, равный половине развёрнутого угла, называется прямым углом
- 9. Острый, тупой и прямой углыУгол называется острым,
- 10. 11. Два угла, у которых одна сторона
- 11. AB MNMN AB13. Две прямые, образующие при пересечении прямые углы, называются перпендикулярными
- 12. Точки А, В и С – вершины
- 13. С В 15. Два треугольника называются
- 14. AB = A1B1AC = A1C1A = A116.
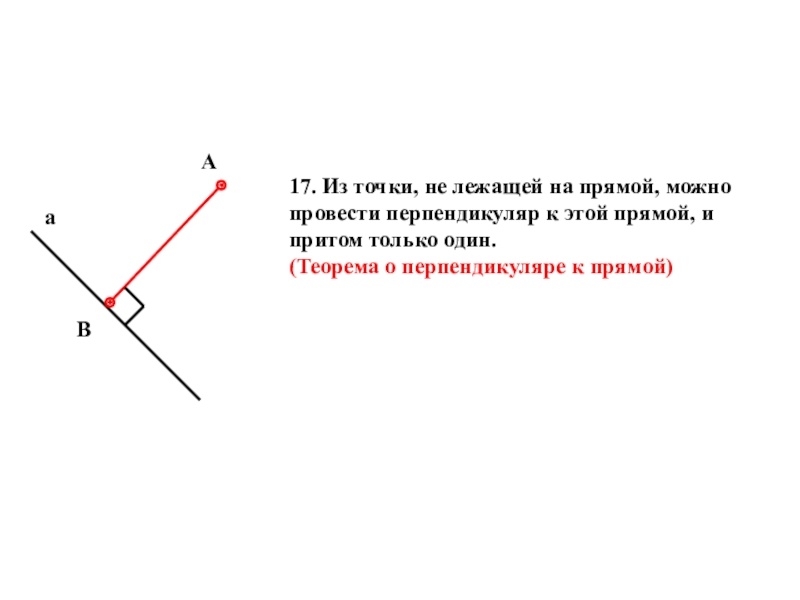
- 15. АВа17. Из точки, не лежащей на прямой,
- 16. АВМС18. Отрезок, соединяющий вершину с серединой противолежащей стороны, называется медианой треугольника
- 17. ВСSА19. Отрезок биссектрисы угла, соединяющий вершину и точку на противолежащей стороне, называется биссектрисой треугольника
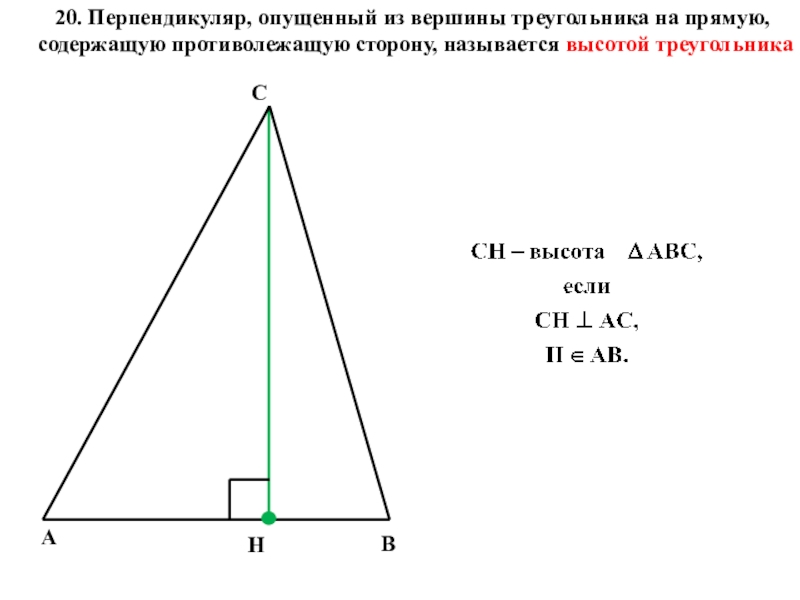
- 18. АВНС20. Перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону, называется высотой треугольника
- 19. NMFPKSONP ∩ FS ∩ MK = O....21. Замечательное свойство треугольникаМедианны треугольника пересекаются в одной точке
- 20. S1
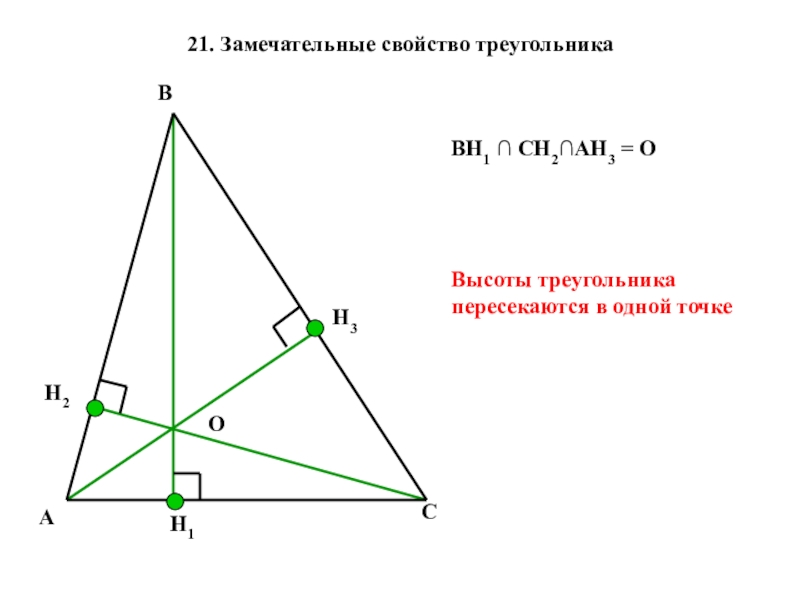
- 21. 21. Замечательные свойство треугольникаАВСH1H3H2Высоты треугольника пересекаются в одной точкеВН1 ∩ СН2∩АН3 = ОО
- 22. АВСАВ, ВС - боковые стороны равнобедренного треугольника
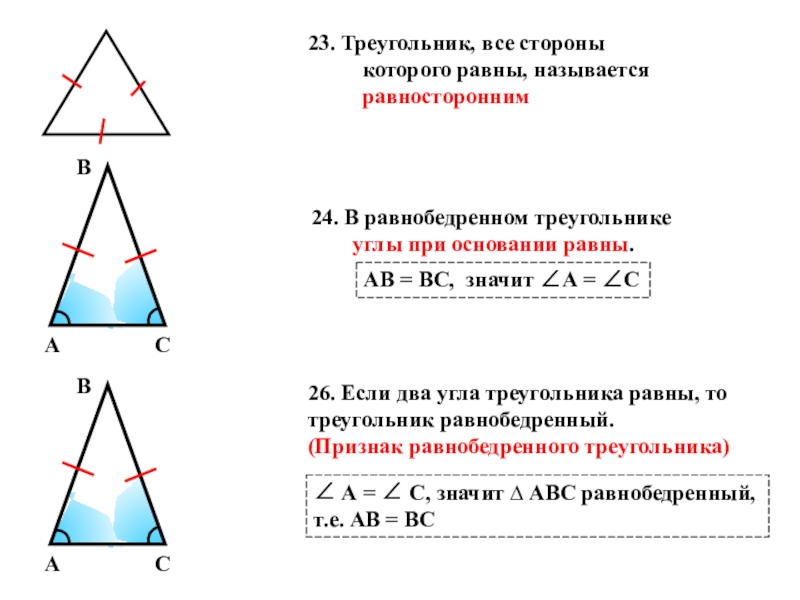
- 23. 23. Треугольник, все стороны которого
- 24. 1 = 2 = 90°
- 25. 1 = 2 = 90°
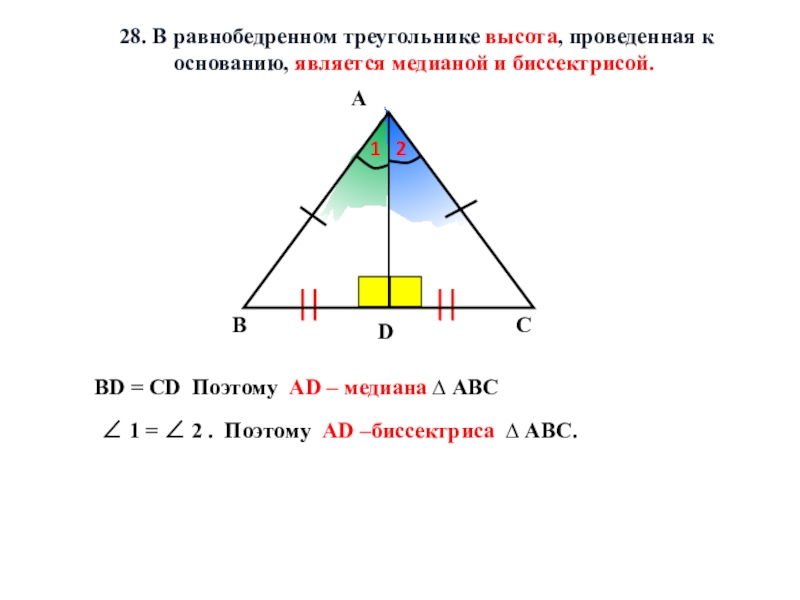
- 26. 1 = 2 . Поэтому
- 27. AB = A1B1A = A129. Второй признак
- 28. 30. Третий признак равенства треугольников. Если три
- 29. 31. Окружностью называется геометрическая фигура, состоящая из
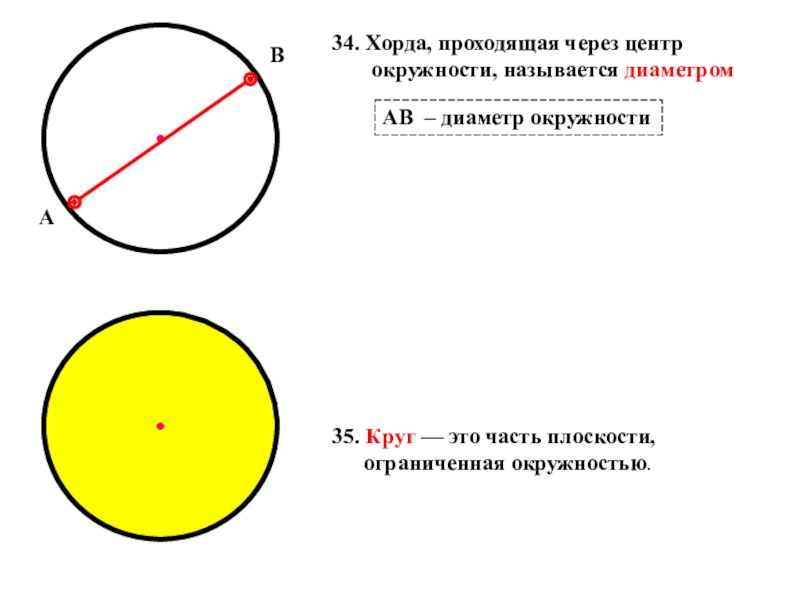
- 30. •АВАВ - радиус•А- центр окружностиАВ – диаметр
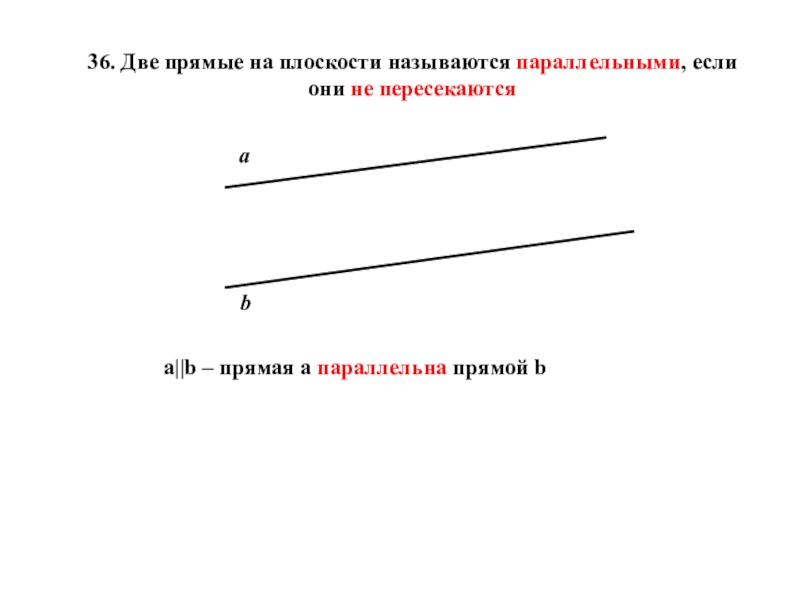
- 31. 36. Две прямые на плоскости называются параллельными,
- 32. Прямая с называется секущей по отношению к
- 33. 38. Если при пересечении двух прямых секущей
- 34. 41. Исходные положения, на основе которых доказываются
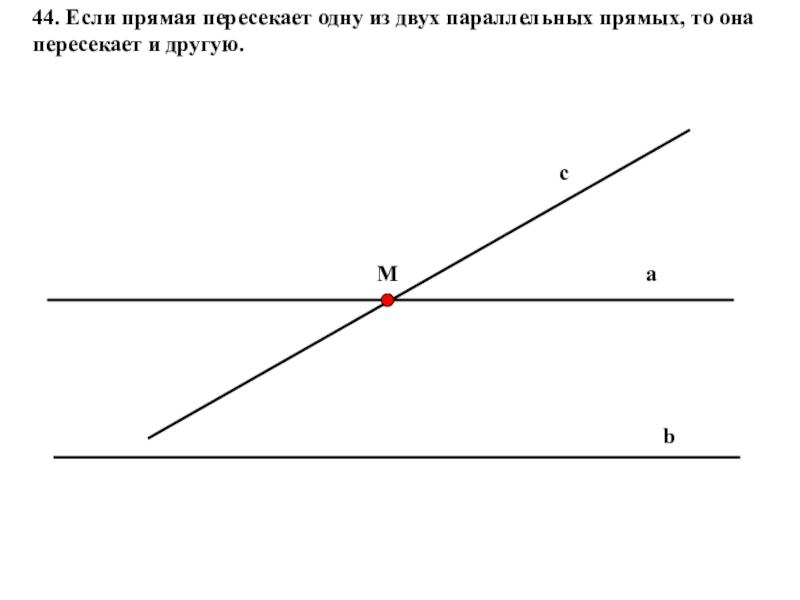
- 35. 44. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую. Маbс
- 36. 45. Если две прямые параллельны третьей прямой,
- 37. 46. Во всякой теореме две
- 38. 49. Если две параллельные прямые пересечены секущей,
- 39. 51. Сумма углов треугольника равна 1800.
- 40. 52. Внешним углом треугольника называется угол смежный
- 41. 54. Треугольник, у которого все три угла
- 42. 59. В треугольнике против большей
- 43. 61. Сумма двух острых углов прямоугольного треугольника
- 44. 64. Если катеты одного прямоугольного
- 45. 66. Если гипотенуза и острый
- 46. 68. Расстоянием от точки до прямой называется
- 47. Федеральный компонент государственного образовательного стандарта основного общего
отрезок1. Отрезок – часть прямой, ограниченная с двух сторон.2. Луч — это часть прямой, ограниченная одной точкой. Эта точка называется началом лучаNЛуч FN
Слайд 2отрезок
1. Отрезок – часть прямой, ограниченная с двух сторон.
2. Луч —
это часть прямой, ограниченная одной точкой. Эта точка называется началом луча
N
Луч FN
Слайд 3Стороны угла – лучи ВА и ВМ.
В
М
Вершина угла – точка
В
А
Луч ВА
Луч ВМ
Угол
АВМ
3. Угол – это геометрическая фигура, которая состоит
из точки и двух лучей, исходящих из этой точки.
Слайд 5Ф1
Ф2
Ф2
Ф1 = Ф2
5. Две геометрические фигуры называются равными, если их можно
совместить наложением.
Слайд 6А
В
Точка С – середина отрезка
6. Точка отрезка, делящая его пополам, называется
серединой отрезка.
Слайд 7В
М
А
АВО = ОВМ
O
Луч ВО – биссектриса угла АВМ
7. Луч,
исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла.
Слайд 9Острый, тупой и прямой углы
Угол называется острым, если он меньше 90°
(т.е. меньше прямого угла).
О
R
T
A
B
C
X
Y
Z
Острый угол
Тупой угол
Прямой угол
10. Угол называется тупым, если он больше 90°, но меньше 180°. (т.е. больше прямого, но меньше развёрнутого).
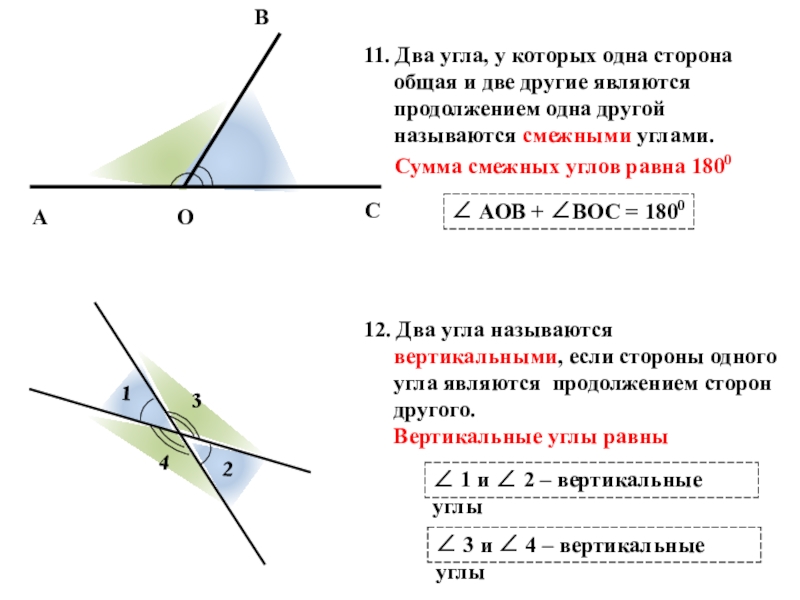
Слайд 1011. Два угла, у которых одна сторона общая и две другие
являются продолжением одна другой называются смежными углами.
Сумма смежных углов равна 1800
Сумма смежных углов равна 1800
АОВ + ВОС = 1800
12. Два угла называются вертикальными, если стороны одного угла являются продолжением сторон другого.
Вертикальные углы равны
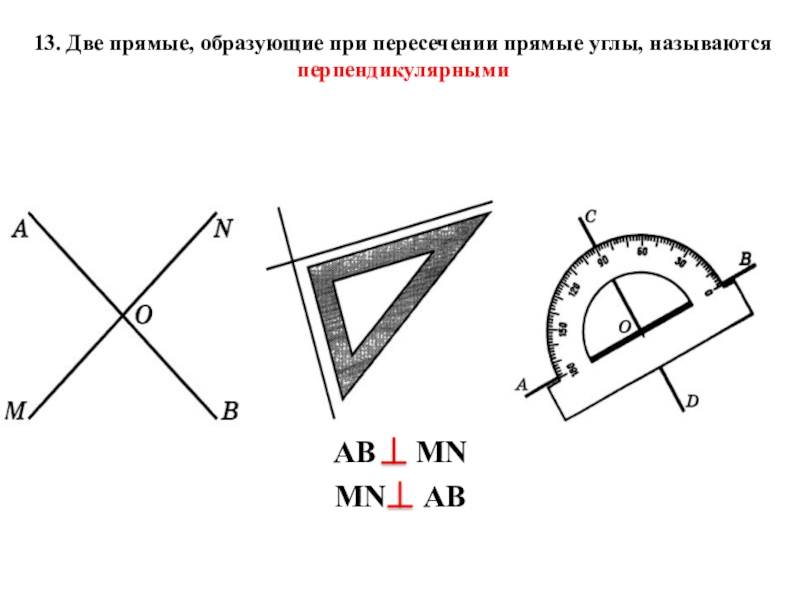
Слайд 11AB MN
MN AB
13. Две прямые, образующие при
пересечении прямые углы, называются
перпендикулярными
перпендикулярными
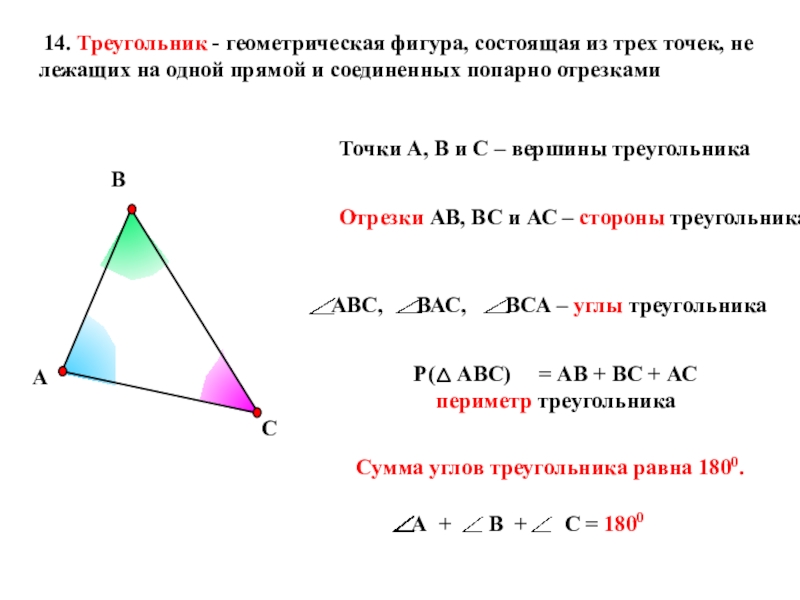
Слайд 12Точки А, В и С – вершины треугольника
Отрезки АВ, ВС и
АС – стороны треугольника
Р( АВС) = АВ + ВС + АС
периметр треугольника
14. Треугольник - геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой и соединенных попарно отрезками
Сумма углов треугольника равна 1800.
Слайд 13С
В
15. Два треугольника называются равными, если их можно
совместить наложением.
Если два треугольника равны, то элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
А
Слайд 14AB = A1B1
AC = A1C1
A = A1
16. Первый признак равенства треугольников.
Если
две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Слайд 15А
В
а
17. Из точки, не лежащей на прямой, можно провести перпендикуляр к
этой прямой, и притом только один.
(Теорема о перпендикуляре к прямой)
(Теорема о перпендикуляре к прямой)
Слайд 16А
В
М
С
18. Отрезок, соединяющий вершину с серединой противолежащей
стороны, называется медианой треугольника
Слайд 17В
С
S
А
19. Отрезок биссектрисы угла, соединяющий вершину и точку на противолежащей стороне,
называется биссектрисой треугольника
Слайд 18А
В
Н
С
20. Перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону,
называется высотой треугольника
Слайд 19N
M
F
P
K
S
O
NP ∩ FS ∩ MK = O
.
.
.
.
21. Замечательное свойство треугольника
Медианны треугольника
пересекаются в одной точке
Слайд 20S1
S2
S3
O
21. Замечательное свойство треугольника
Биссектрисы треугольника пересекаются в одной точке
С
В
А
AS1 ∩ BS2∩АCS3 = О
Слайд 2121. Замечательные свойство треугольника
А
В
С
H1
H3
H2
Высоты треугольника пересекаются в одной точке
ВН1 ∩ СН2∩АН3
= О
О
Слайд 22А
В
С
АВ, ВС - боковые стороны равнобедренного треугольника
А, С –
углы при основании равнобедренного треугольника
АС - основание равнобедренного треугольника
В – угол при вершине равнобедренного
треугольника
22. Треугольник называется равнобедренным, если две его стороны равны
Слайд 2323. Треугольник, все стороны которого равны, называется равносторонним
24. В
равнобедренном треугольнике
углы при основании равны.
углы при основании равны.
АВ = ВС, значит А = С
26. Если два угла треугольника равны, то треугольник равнобедренный. (Признак равнобедренного треугольника)
А = С, значит ∆ АВС равнобедренный, т.е. АВ = ВС
Слайд 24 1 = 2 = 90° (смежные углы), поэтому AD
–высота ∆ АВС.
25. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
BD = CD, поэтому AD – медиана ∆ АВС
В
D
С
А
Слайд 25 1 = 2 = 90° (смежные углы), поэтому AD
–высота ∆ АВС.
В
А
D
С
27. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
3 = 4 , поэтому AD – биссектриса ∆ АВС
3
4
Слайд 26 1 = 2 . Поэтому AD –биссектриса ∆ АВС.
28. В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
BD = CD Поэтому AD – медиана ∆ АВС
В
D
С
А
1
2
Слайд 27AB = A1B1
A = A1
29. Второй признак равенства треугольников.
Если сторона и
два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
В = В1
Слайд 2830. Третий признак равенства треугольников.
Если три стороны одного треугольника соответственно равны
трем сторонам другого треугольника, то такие треугольники равны.
Слайд 2931. Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на
заданном расстоянии от данной точки. Эта точка называется центром окружности
•
А
В
•
АВ - радиус
•А- центр окружности
32. Радиус окружности – отрезок, соединяющий центр окружности с какой-либо её точкой.
АВ – радиус окружности
А – центр окружности
В – точка на окружности
•
С
D
33. Отрезок, соединяющий две точки окружности, называется ее хордой.
CD – хорда окружности
Слайд 30•
А
В
АВ - радиус
•А- центр окружности
АВ – диаметр окружности
34. Хорда, проходящая через
центр окружности, называется диаметром
•
35. Круг — это часть плоскости, ограниченная окружностью.
Слайд 3136. Две прямые на плоскости называются параллельными, если они не пересекаются
a||b
– прямая а параллельна прямой b
Слайд 32Прямая с называется секущей по отношению к прямым а и в,
если она пересекает их в двух точках
37. При пересечении двух прямых секущей образуется восемь углов: накрест лежащие, односторонние и соответственные.
Накрест лежащие углы: 3 и 5, 4 и 6
Односторонние углы: 4 и 5, 3 и 6
Соответственные углы: 1 и 5, 4 и 8,
2 и 6, 3 и 7.
Слайд 3338. Если при пересечении двух прямых секущей накрест лежащие углы равны,
то прямые параллельны.
1 = 2, значит a II b
39. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
3 = 4, значит a II b
40. Если при пересечении двух прямых секущей сумма внутренних односторонних углов равна 180˚, то прямые параллельны
1 + 2 = 1800 , значит a II b
Слайд 3441. Исходные положения, на основе которых доказываются теоремы, называются аксиомами.
42.
Например, аксиомой является утверждение о том, что через любые две точки проходит прямая, и притом только одна.
А
В
43. Аксиома параллельных прямых. Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
а
b
М
с
a || b
Слайд 3544. Если прямая пересекает одну из двух параллельных прямых, то она
пересекает и другую.
М
а
b
с
Слайд 3645. Если две прямые параллельны третьей прямой, то они параллельны
с
b
а
a
|| с и b || с, значит a || b
Слайд 37 46. Во всякой теореме две части: условие (то, что дано) и
заключение (то, что требуется доказать).
47. Теоремой, обратной данной, называется такая теорема, в которой условием является заключение данной теоремы, а заключением – условие данной теоремы.
48. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
a II b, значит 1= 2
Слайд 3849. Если две параллельные прямые пересечены секущей, то соответственные углы равны.
a II b, значит 1= 2
50. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 1800.
a II b, значит 3+ 4 = 1800
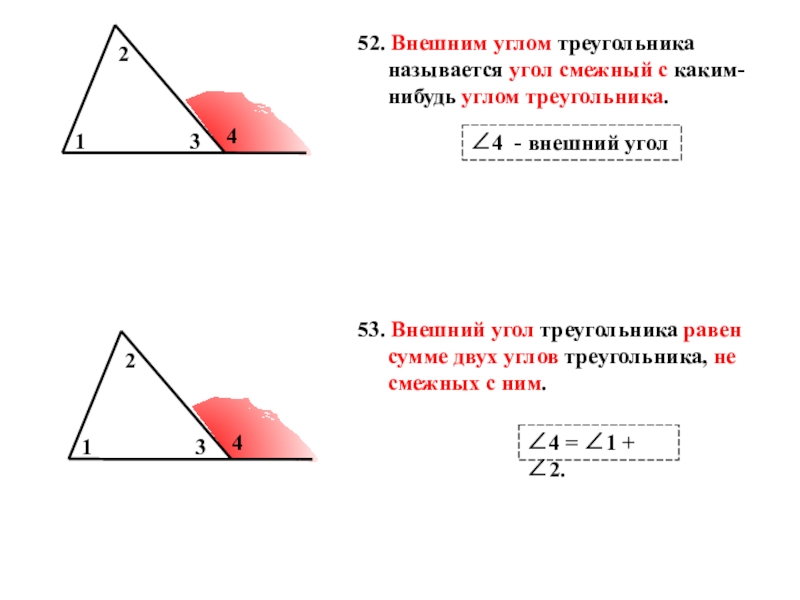
Слайд 4052. Внешним углом треугольника называется угол смежный с каким-нибудь углом треугольника.
53.
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
4 = 1 + 2.
4 - внешний угол
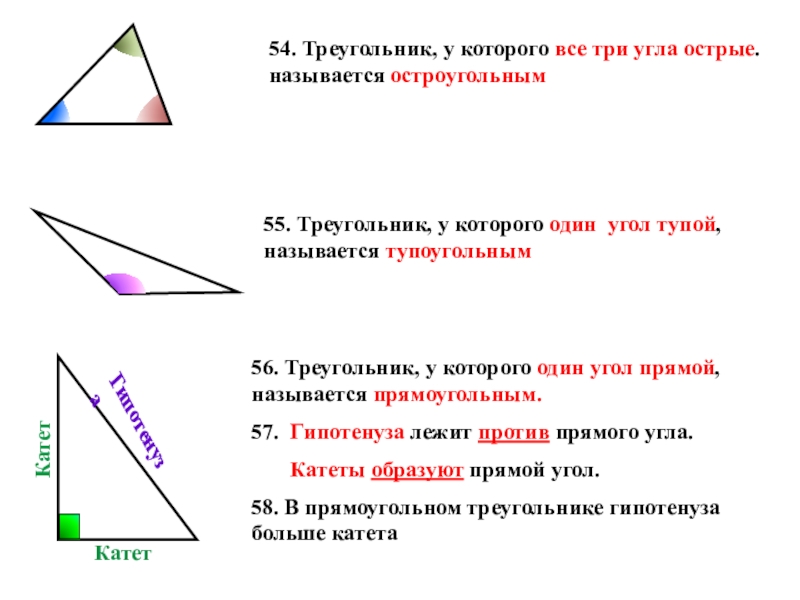
Слайд 4154. Треугольник, у которого все три угла острые. называется остроугольным
56. Треугольник,
у которого один угол прямой, называется прямоугольным.
57. Гипотенуза лежит против прямого угла.
Катеты образуют прямой угол.
58. В прямоугольном треугольнике гипотенуза больше катета
57. Гипотенуза лежит против прямого угла.
Катеты образуют прямой угол.
58. В прямоугольном треугольнике гипотенуза больше катета
55. Треугольник, у которого один угол тупой, называется тупоугольным
Слайд 42 59. В треугольнике против большей стороны лежит больший угол
АВ
> АС, значит С > В
В треугольнике против большего угла лежит большая сторона
С > В, значит АВ > АС
60. Каждая сторона треугольника меньше суммы двух других сторон. ( Неравенство треугольника)
АС АВ + ВС
АВ АС + ВС
ВС АС + АВ
Слайд 4361. Сумма двух острых углов прямоугольного треугольника равна 90°
62. Катет прямоугольного
треугольника , лежащий против угла в 30°, равен половине гипотенузы.
63. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
А + В = 900
Свойства прямоугольного треугольника
Слайд 44 64. Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то
такие треугольники равны. (Признак равенства прямоугольных треугольников по двум катетам)
65. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого, то такие треугольники равны. (Признак равенства прямоугольных треугольников по катету и острому углу)
Слайд 45 66. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны
гипотенузе и острому углу другого, то такие треугольники равны. (Признак равенства прямоугольных треугольников по гипотенузе и острому углу)
67. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны. (Признак равенства прямоугольных треугольников по гипотенузе и катету)
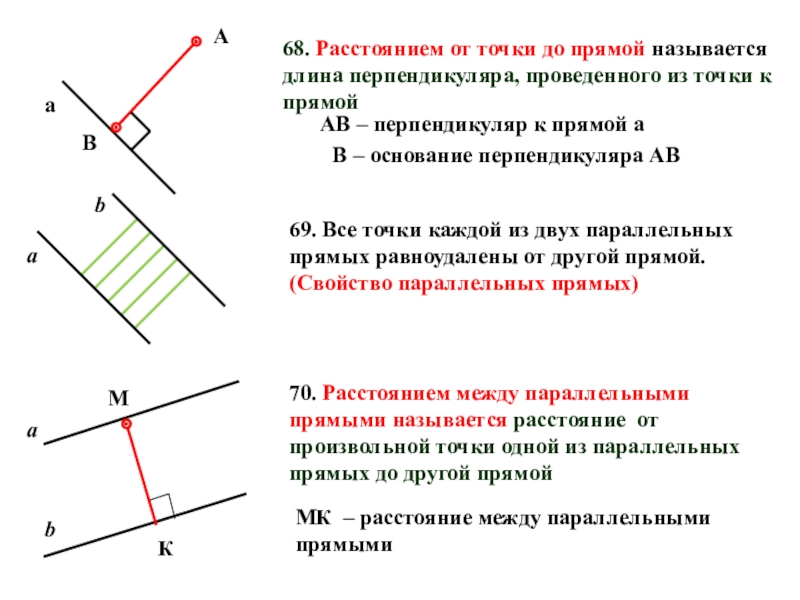
Слайд 4668. Расстоянием от точки до прямой называется длина перпендикуляра, проведенного из
точки к прямой
М
а
b
К
70. Расстоянием между параллельными прямыми называется расстояние от произвольной точки одной из параллельных прямых до другой прямой
А
В
а
АВ – перпендикуляр к прямой а
В – основание перпендикуляра АВ
МК – расстояние между параллельными прямыми
69. Все точки каждой из двух параллельных прямых равноудалены от другой прямой. (Свойство параллельных прямых)
Слайд 47Федеральный компонент государственного образовательного стандарта основного общего образования по математике (пр.министерства
образования РФ №1089 от 05.03.2004г).
Авторская программа Атанасян Л.С., Бутузов В.Ф., Кодомцев С.Б. составитель БурмистроваТ.А., М. «Просвещение», 2015
УМК «Геометрия 7-9» Атанасян Л.С., Бутузов В.Ф.,и др- М.:Просвещение, 2015г
Интернет – ресурсы: http://le-savchen.uCoz.ru
Авторская программа Атанасян Л.С., Бутузов В.Ф., Кодомцев С.Б. составитель БурмистроваТ.А., М. «Просвещение», 2015
УМК «Геометрия 7-9» Атанасян Л.С., Бутузов В.Ф.,и др- М.:Просвещение, 2015г
Интернет – ресурсы: http://le-savchen.uCoz.ru
Литература:
