- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Справочник по геометрии (9 класс)
Содержание
- 1. Презентация по математике на тему Справочник по геометрии (9 класс)
- 2. 2. Длиной или модулем вектора называется длина
- 3. 3. Любая точка плоскости также
- 4. 5. Ненулевые векторы называются коллинеарными,
- 5. Коллинеарные, противоположно направленные векторы
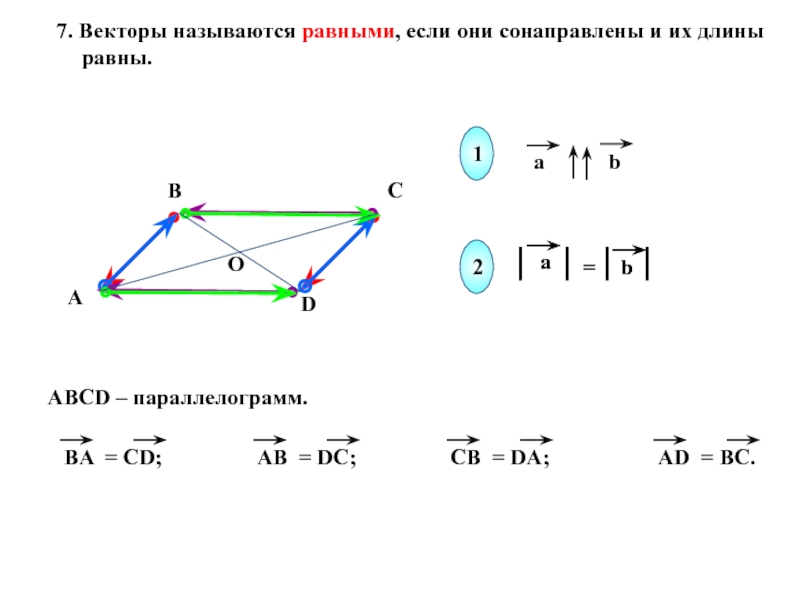
- 6. 7. Векторы называются равными, если они сонаправлены и их длины равны.12
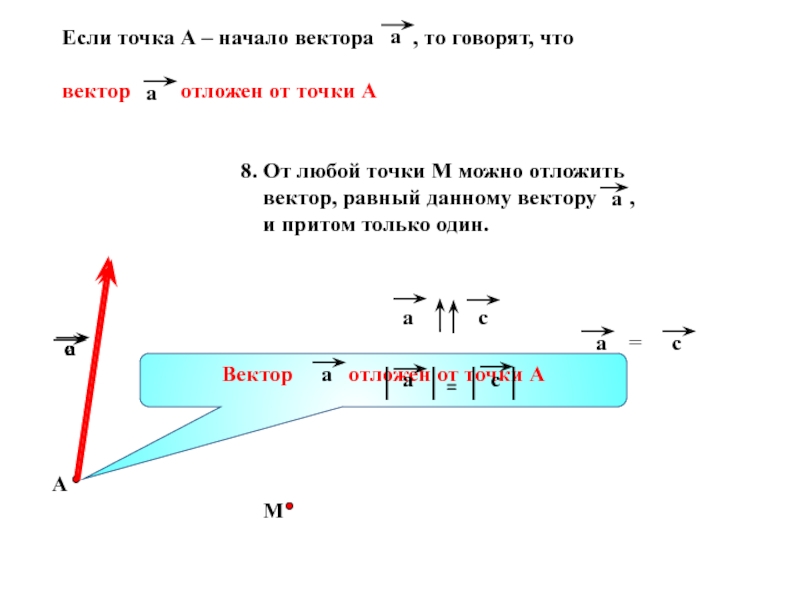
- 7. Если точка А –
- 8. 9. Вектор а
- 9. Законы сложения векторов10. Для любых векторов а,
- 10. Вычитание векторов11. Разностью двух векторов а и
- 11. Умножение вектора на число13.Произведением ненулевого вектора а
- 12. Умножение вектора на число17. Для любых чисел
- 13. 18. Координаты суммы векторов равны сумме соответствующих
- 14. 23.24.22. Каждая координата середины отрезка равна полусумме
- 15. 27. А(х0; у0) – центр окружности
- 16. 29. Формулы приведения30. Площадь треугольника равна половине произведения его сторон на синус угла между ними.
- 17. 31. Теореме синусов
- 18. Дано:Найти: c, AC = b BC =
- 19. Дано:Найти: с, b, Решение: ABC34.
- 20. Решение:35. Решение треугольника по трем сторонамПользуясь теоремой
- 21. 36. Скалярным произведением двух векторов называется произведение
- 22. Действия над векторами(свойства)40. Свойства скалярного произведения векторов
- 23. 41. Выпуклый многоугольник называется правильным, если у
- 24. 42. Сумма всех углов правильного
- 25. 44. Около всякого правильного многоугольника можно описать
- 26. 51. Вычисление угла правильного многоугольника: 48. Площадь
- 27. S = πR253. Площадь круга52. Длина окружности54.
- 28. Федеральный компонент государственного образовательного стандарта основного общего
Слайд 1Справочник по геометрии
9 класс
Из опыта работы учителя математики
МБОУ «СОШ
Султангалиной Г.Г.
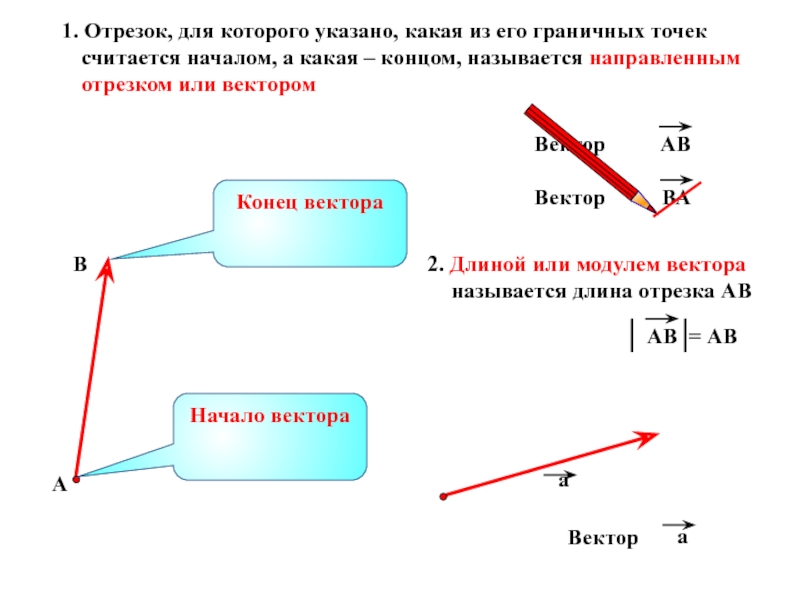
Слайд 22. Длиной или модулем вектора называется длина отрезка АВ
Начало вектора
Конец вектора
Слайд 3 3. Любая точка плоскости также является вектором.
4. Длина нулевого вектора считается равной нулю
Начало нулевого вектора совпадает с его концом, поэтому нулевой вектор не имеет какого-либо определенного направления. Иначе говоря, любое направление можно считать направлением нулевого вектора.
Слайд 4 5. Ненулевые векторы называются коллинеарными, если они лежат на
Коллинеарные, сонаправленные векторы
Слайд 5
Коллинеарные, противоположно направленные векторы
5. Ненулевые векторы называются
6. Нулевой вектор считается коллинеарным, сонаправленным с любым вектором.
Слайд 8
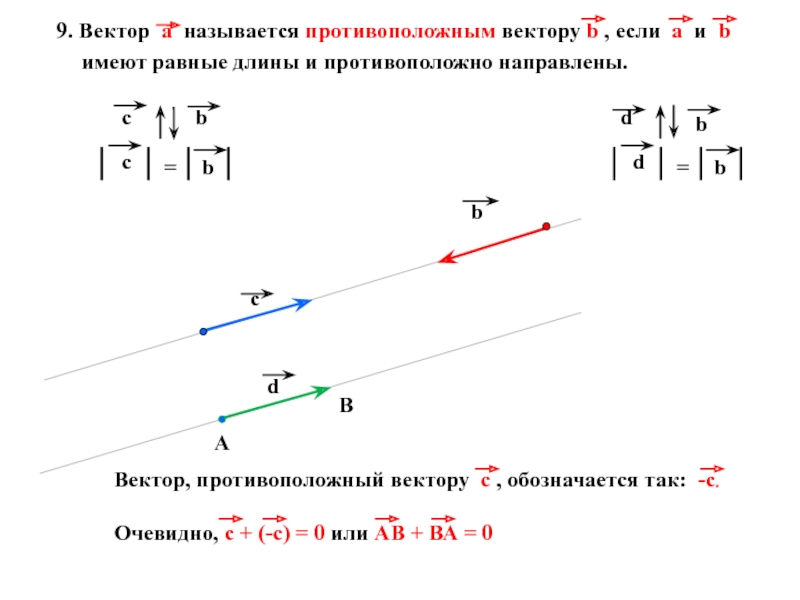
9. Вектор а называется противоположным вектору b
А
В
Вектор, противоположный вектору c , обозначается так: -c.
Очевидно, с + (-с) = 0 или АВ + ВА = 0
Слайд 9Законы сложения векторов
10. Для любых векторов а, b, с справедливы равенства
( а + b ) + c = a + ( b + c ) (сочетательный закон)
Правило параллелограмма
Пусть а и b – два вектора. Отметим произвольную точку А отложим от этой точки АВ = а, затем вектор АD = b. На этих векторах построим параллелограмм АВСD.
АС = АВ + BС = а + b
АС = АD + DС = b + a
a
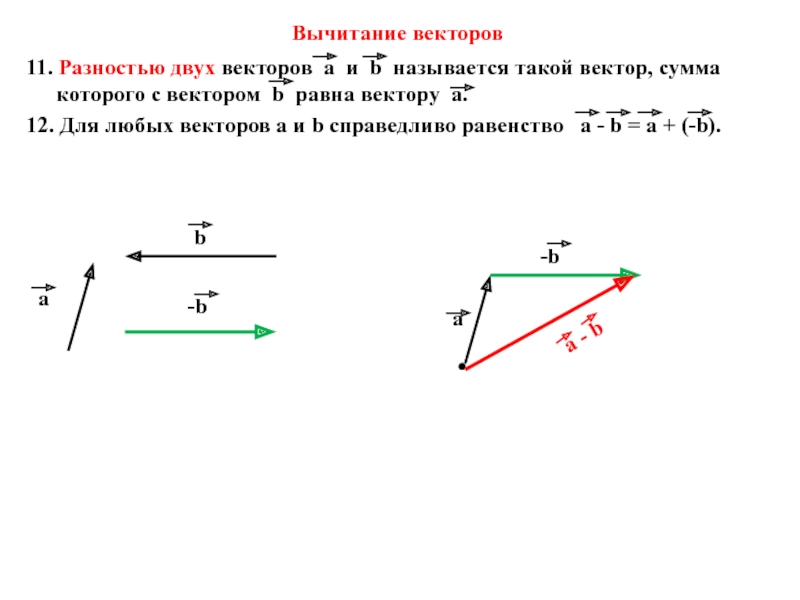
Слайд 10Вычитание векторов
11. Разностью двух векторов а и b называется такой вектор,
12. Для любых векторов а и b справедливо равенство а - b = а + (-b).
а
а
b
-b
-b
a - b
Слайд 11Умножение вектора на число
13.Произведением ненулевого вектора а на число k называется
14. Произведением нулевого вектора на любое число считается нулевой вектор.
16. Для любого числа k и любого вектора а векторы а и ka коллинеарные.
15. Произведение любого вектора на число нуль есть нулевой вектор.
Слайд 12Умножение вектора на число
17. Для любых чисел k, n и любых
(kn) а = k (na) (сочетательный закон)
(k+n) а = kа + na (первый распределительный закон)
k( а+ b ) = kа + kb (второй распределительный закон)
Свойства действий над векторами позволяют в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования по тем же правилам, что и в числовых выражениях. Например,
p = 2( a – b) + ( c + a ) – 3( b – c + a ) =
= 2a – 2b + c + a – 3b + 3c – 3a = - 5b + 4c
Слайд 1318. Координаты суммы векторов равны сумме соответствующих координат этих векторов.
19. Координаты
20. Координаты произведения вектора на число равны произведению соответствующих координат вектора на это число.
21. Каждая координата вектора равна
разности соответствующих координат его конца и начала.
А(х1 ;у1), В(х2 ;у2)
АВ {х2 - х1; у2 - у1}
Слайд 1423.
24.
22. Каждая координата середины отрезка равна полусумме соответствующих координат её концов
С(х
25. Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.
MN – средняя линия трапеции АВСD
26. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Слайд 1527. А(х0; у0) – центр окружности
В(х; у)
r – радиус окружности
Уравнение окружности:
(х-х0)² + (у-у0)² = r²
Уравнение окружности с центром в начале координат: х² + у² = r²
(0;0) – центр окружности, r – радиус окружности
28. Прямая на плоскости задается уравнением
ax + by + c = 0,
где a, b, c - некоторые числа, причем
a,b одновременно не равны нулю
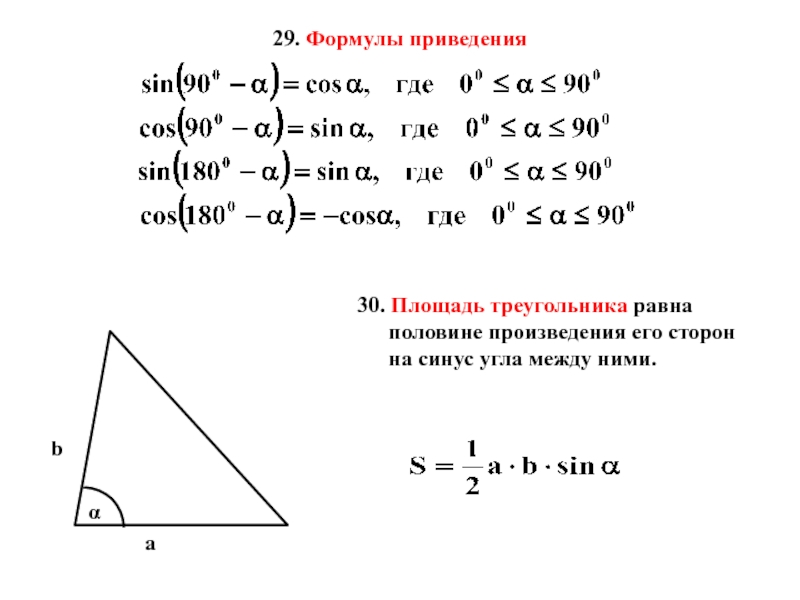
Слайд 1629. Формулы приведения
30. Площадь треугольника равна половине произведения его сторон на
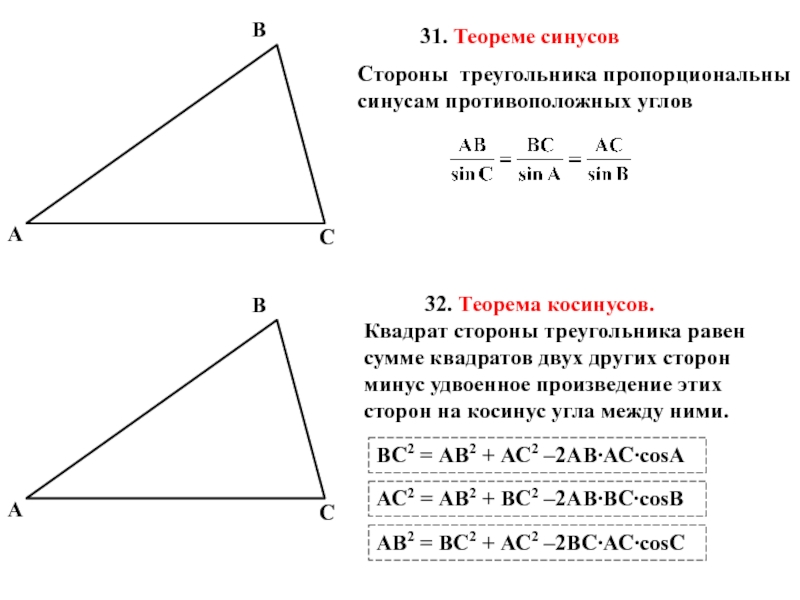
Слайд 1731. Теореме синусов
32. Теорема
ВС2 = АВ2 + АС2 –2АВ∙АС∙cosA
Стороны треугольника пропорциональны синусам противоположных углов
АС2 = АВ2 + ВС2 –2АВ∙ВС∙cosВ
АВ2 = ВС2 + АС2 –2ВС∙АС∙cosС
Слайд 18Дано:
Найти: c,
AC = b
BC = a
33. Решение треугольника по
С
А,
В
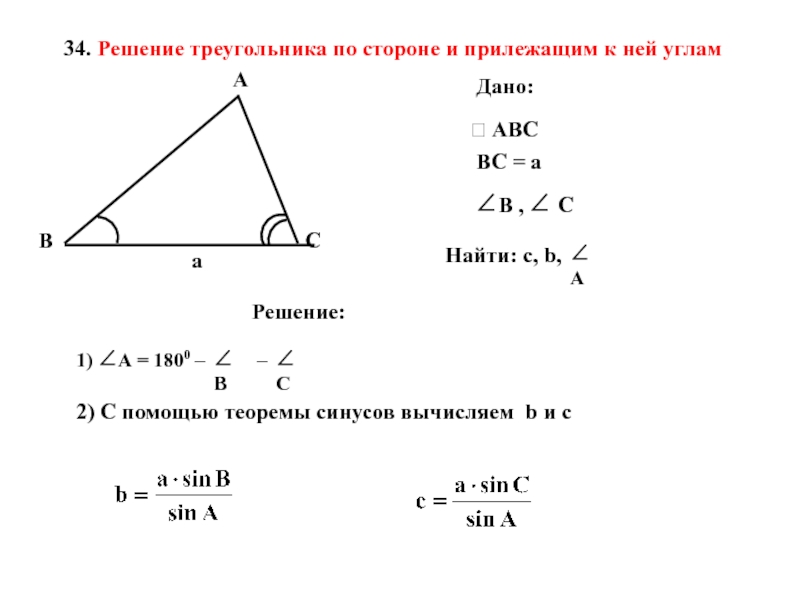
Слайд 19Дано:
Найти: с, b,
Решение:
ABC
34. Решение треугольника по стороне
ВC = а
В , С
А
Слайд 20Решение:
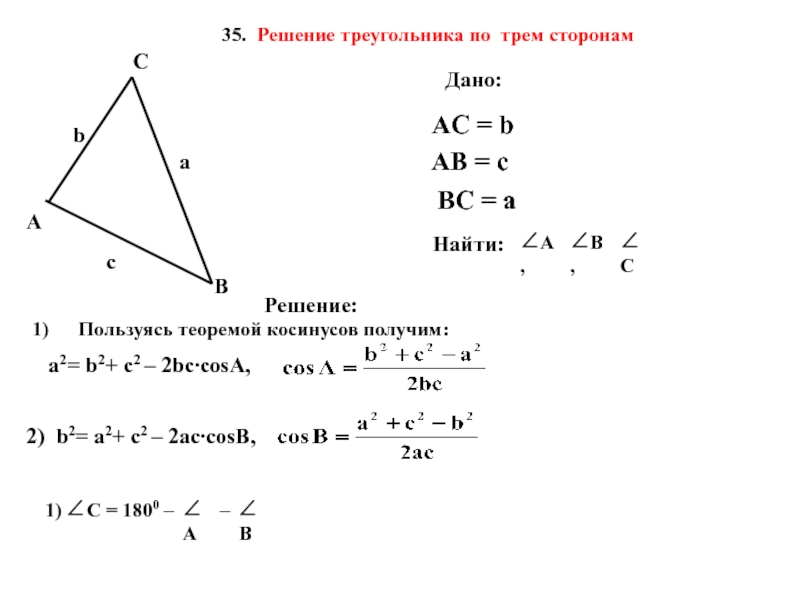
35. Решение треугольника по трем сторонам
Пользуясь теоремой косинусов получим:
а2= b2+
2) b2= a2+ c2 – 2ac∙cosB,
1) C = 1800 –
A
B
–
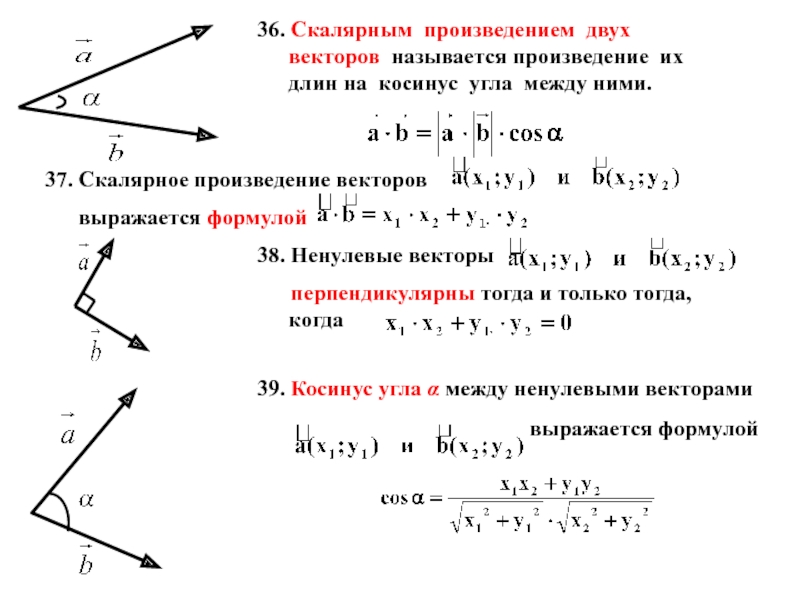
Слайд 2136. Скалярным произведением двух векторов называется произведение их длин на косинус
37. Скалярное произведение векторов
выражается формулой
38. Ненулевые векторы
перпендикулярны тогда и только тогда, когда
39. Косинус угла α между ненулевыми векторами
выражается формулой
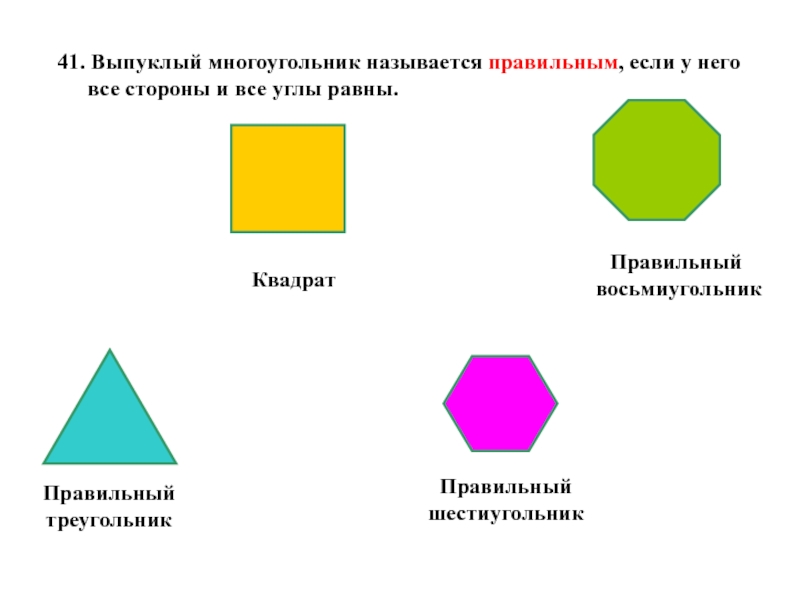
Слайд 2341. Выпуклый многоугольник называется правильным, если у него все стороны и
Правильный
треугольник
Квадрат
Правильный
шестиугольник
Правильный
восьмиугольник
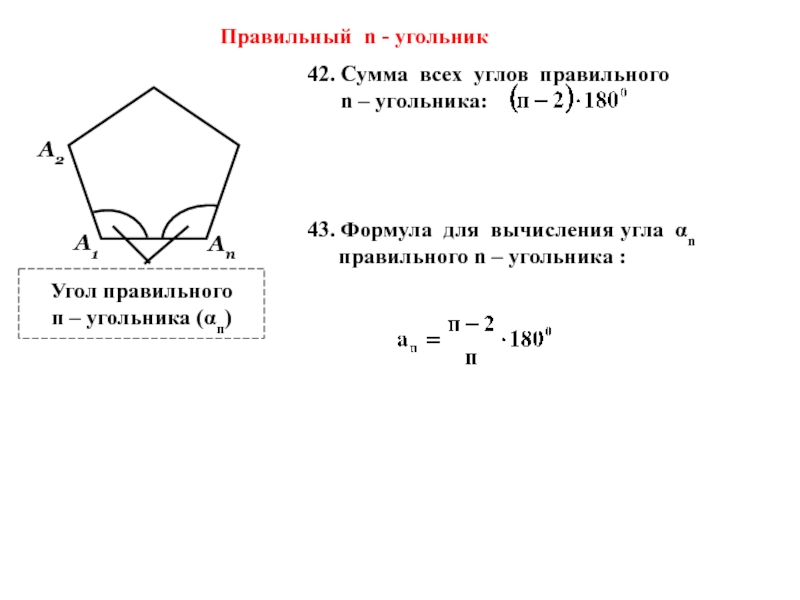
Слайд 2442. Сумма всех углов правильного
n – угольника:
Правильный n
Угол правильного
п – угольника (αп)
А1
А2
Ап
43. Формула для вычисления угла αn правильного n – угольника :
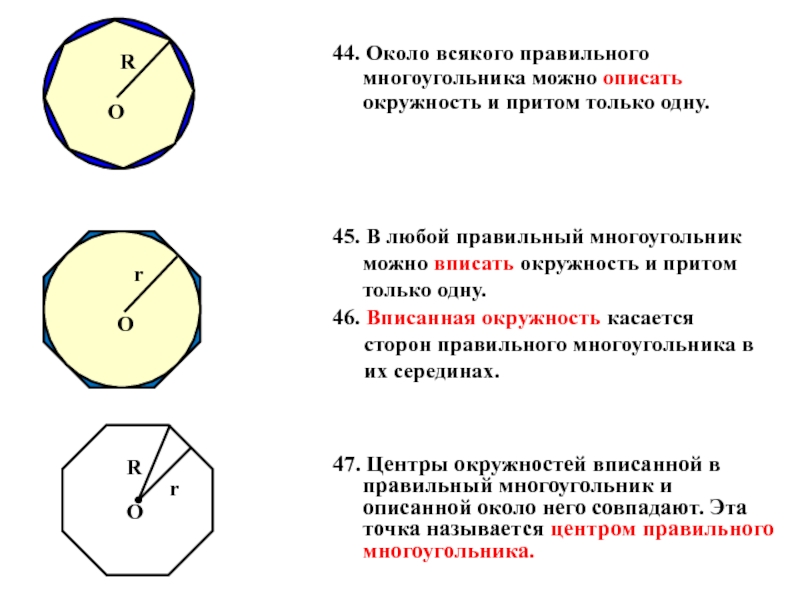
Слайд 2544. Около всякого правильного многоугольника можно описать окружность и притом только
45. В любой правильный многоугольник можно вписать окружность и притом только одну.
46. Вписанная окружность касается сторон правильного многоугольника в их серединах.
47. Центры окружностей вписанной в правильный многоугольник и описанной около него совпадают. Эта точка называется центром правильного многоугольника.
Слайд 2651. Вычисление угла правильного многоугольника:
48. Площадь правильного многоугольника:
49. Сторона
50. Радиус вписанной окружности:
Для правильного треугольника:
Для правильного четырехугольника (квадрата):
Для правильного шестиугольника:
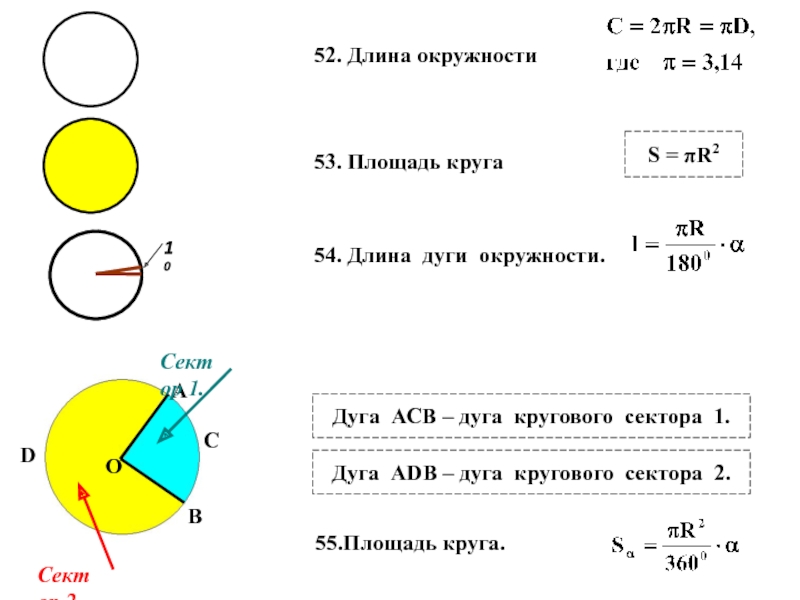
Слайд 27S = πR2
53. Площадь круга
52. Длина окружности
54. Длина дуги окружности.
Дуга АСВ
Дуга АDВ – дуга кругового сектора 2.
55.Площадь круга.
Слайд 28Федеральный компонент государственного образовательного стандарта основного общего образования по математике (пр.министерства
Авторская программа Атанасян Л.С., Бутузов В.Ф., Кодомцев С.Б. составитель БурмистроваТ.А., М. «Просвещение», 2015
УМК «Геометрия 7-9» Атанасян Л.С., Бутузов В.Ф.,и др- М.:Просвещение, 2015г
Интернет – ресурсы: http://le-savchen.uCoz.ru
Литература: