- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Справочник по геометрии (8 класс)
Содержание
- 1. Презентация по математике на тему Справочник по геометрии (8 класс)
- 2. AB||CD, AD||BC1. Параллелограммом называется четырехугольник, у которого
- 3. 4. Если в четырехугольнике две стороны равны
- 4. 7. Трапецией называется четырехугольник, у которого две
- 5. 10. Если на одной из двух прямых
- 6. 11. Прямоугольник – это параллелограмм, у которого
- 7. 14. Ромб – это параллелограмм, у которого
- 8. 16. Квадратом называется прямоугольник, у которого
- 9. 19. S = a2, где a –
- 10. 24. Если высоты треугольников равны, то их
- 11. ∆АВС прямоугольный (∠О прямой), значит ВС2 =
- 12. АВСС1В1А129. Два треугольника называются подобными, если их
- 13. 30. Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
- 14. 31. Отношение площадей двух подобных треугольников равно
- 15. 33. Если две стороны одного треугольника пропорциональны
- 16. 35. Средней линией треугольника называется отрезок, соединяющий
- 17. NMFPKSONP ∩ FS ∩ MK = O37.
- 18. Высота прямоугольного треугольника, проведенная
- 19. 40. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- 20. 41. Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- 21. 42. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
- 22. 44. Sin2 +cos2 = 1 – основное тригонометрическое тождество45.
- 23. 46. Если расстояние от центра окружности до
- 24. Слайд 24
- 25. 51. Угол с вершиной в центре
- 26. 52. Угол, вершина которого лежит на окружности,
- 27. 56. Если хорды окружности пересекаются, то произведение
- 28. Слайд 28
- 29. 61. Серединным перпендикуляром к отрезку называется прямая,
- 30. 65. Если все стороны многоугольника касаются окружности,
- 31. 69. Если все вершины многоугольника лежат на
- 32. Федеральный компонент государственного образовательного стандарта основного общего
Слайд 1Справочник по геометрии
8 класс
Из опыта работы учителя математики
МБОУ «СОШ
Султангалиной Г.Г.
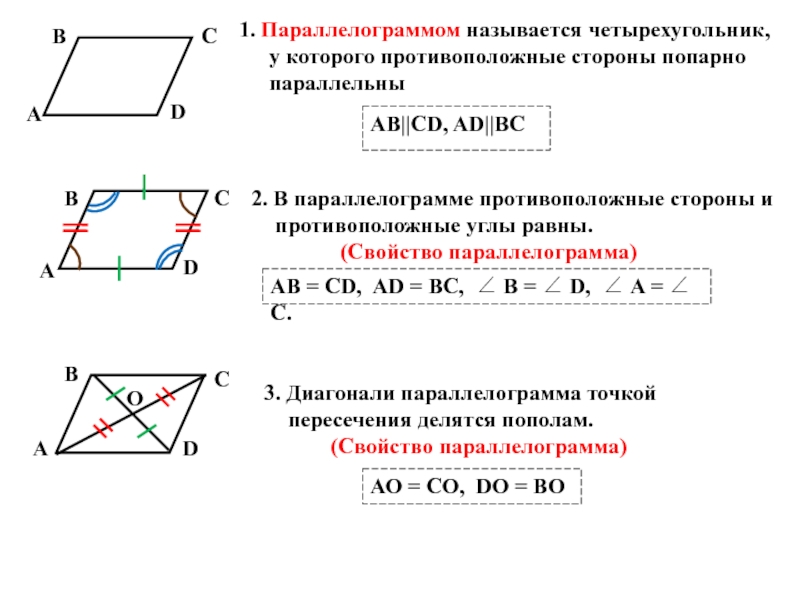
Слайд 2AB||CD, AD||BC
1. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны
2.
(Свойство параллелограмма)
АВ = СD, AD = BC, B = D, A = C.
3. Диагонали параллелограмма точкой пересечения делятся пополам.
(Свойство параллелограмма)
АО = СО, DО = BО
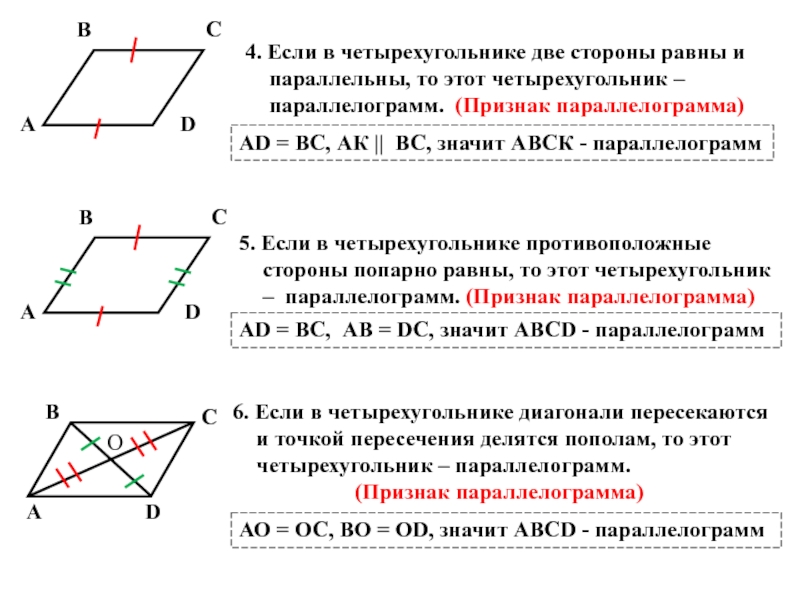
Слайд 34. Если в четырехугольнике две стороны равны и параллельны, то этот
АD = ВС, АК || ВС, значит АВСК - параллелограмм
5. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм. (Признак параллелограмма)
АD = ВС, АВ = DС, значит АВСD - параллелограмм
6. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
(Признак параллелограмма)
АО = ОС, ВО = ОD, значит АВСD - параллелограмм
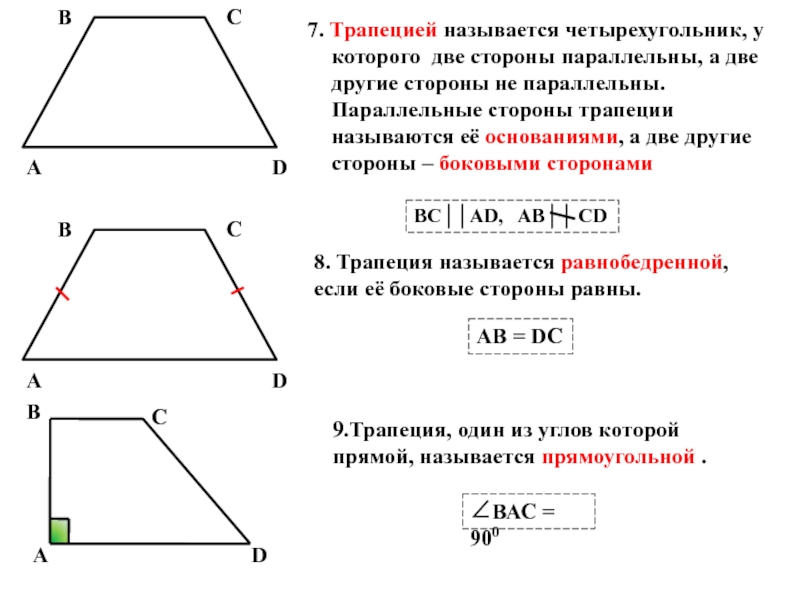
Слайд 47. Трапецией называется четырехугольник, у которого две стороны параллельны, а две
8. Трапеция называется равнобедренной, если её боковые стороны равны.
9.Трапеция, один из углов которой прямой, называется прямоугольной .
BC││AD, AB││ CD
АВ = DC
ВАС = 900
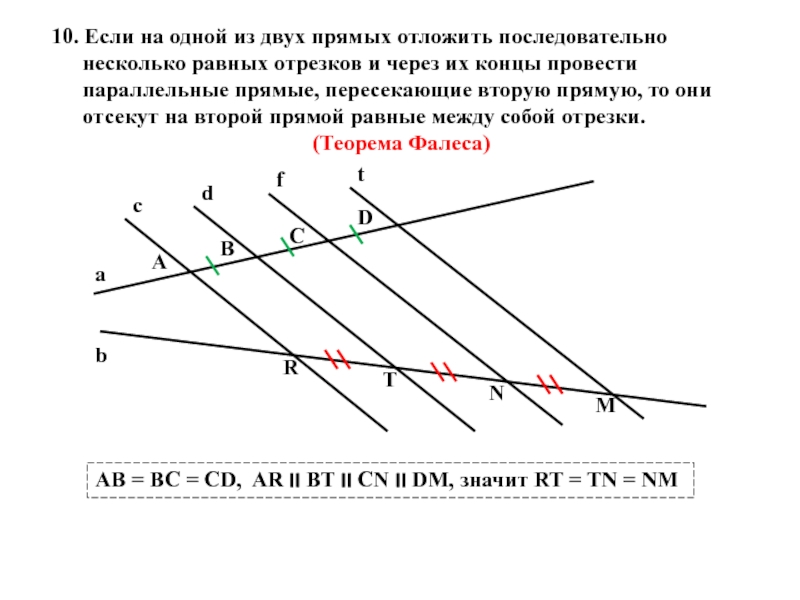
Слайд 510. Если на одной из двух прямых отложить последовательно несколько равных
(Теорема Фалеса)
AB = BC = CD, AR II BT II CN II DM, значит RT = TN = NM
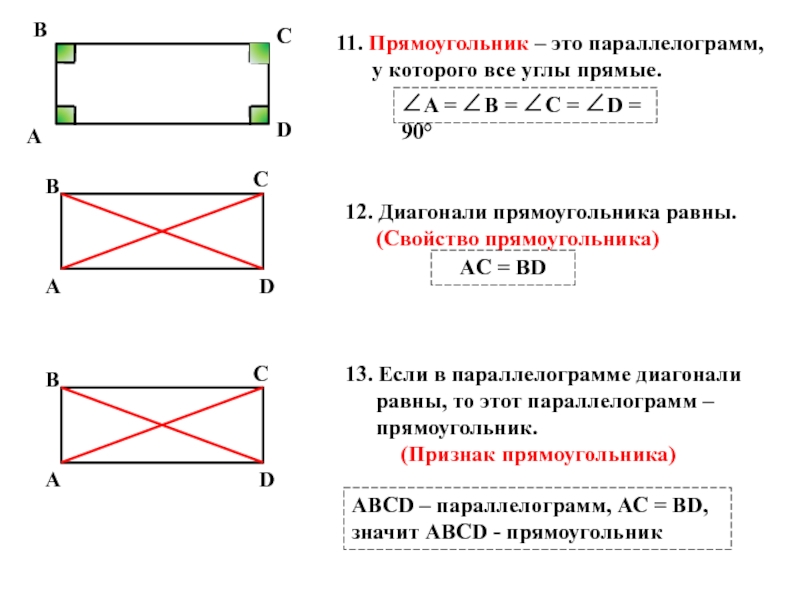
Слайд 611. Прямоугольник – это параллелограмм, у которого все углы прямые.
∠A =
12. Диагонали прямоугольника равны. (Свойство прямоугольника)
AC = BD
13. Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
(Признак прямоугольника)
АВСD – параллелограмм, АС = ВD,
значит АВСD - прямоугольник
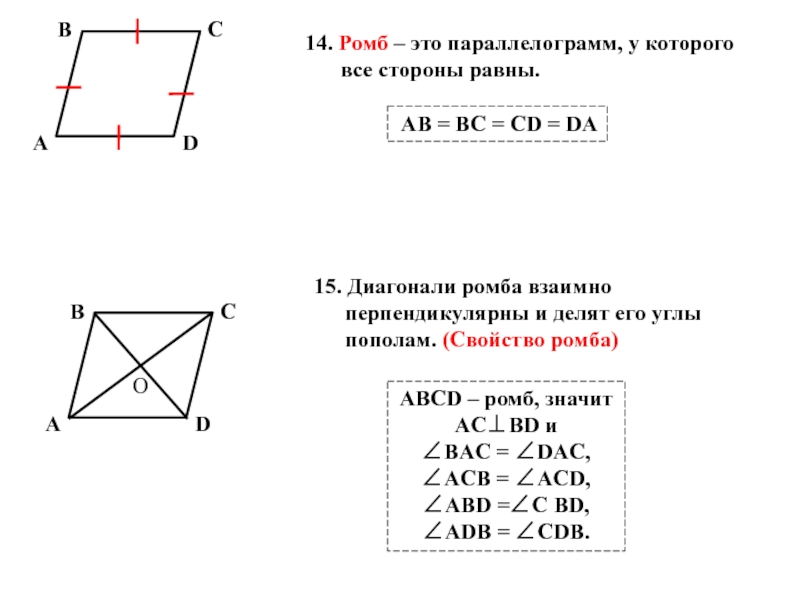
Слайд 714. Ромб – это параллелограмм, у которого все стороны равны.
AB =
15. Диагонали ромба взаимно перпендикулярны и делят его углы пополам. (Свойство ромба)
АВСD – ромб, значит
AC⊥BD и
∠BAC = ∠DAC,
∠AСВ = ∠AСD,
∠AВD =∠С BD,
∠ADВ = ∠СDB.
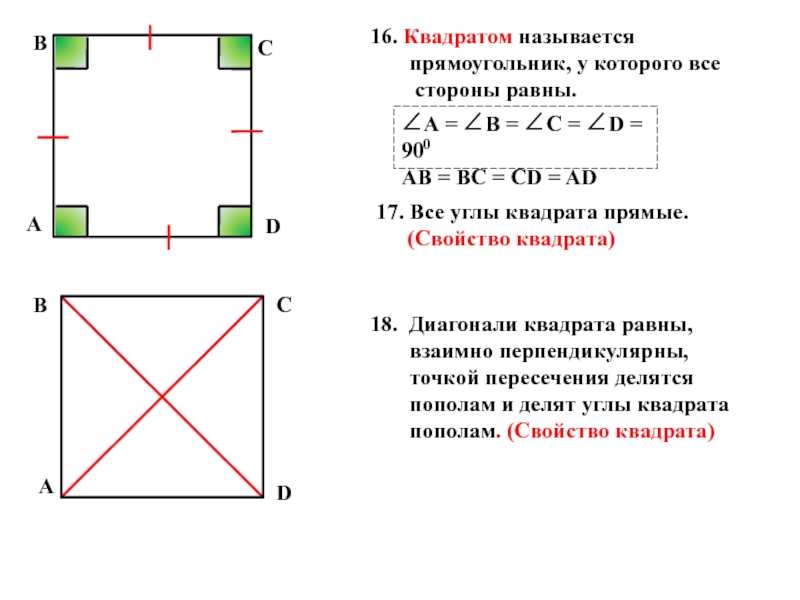
Слайд 816. Квадратом называется прямоугольник, у которого все
стороны равны.
А
D
∠А =
АВ = ВC = CD = AD
17. Все углы квадрата прямые. (Свойство квадрата)
18. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам. (Свойство квадрата)
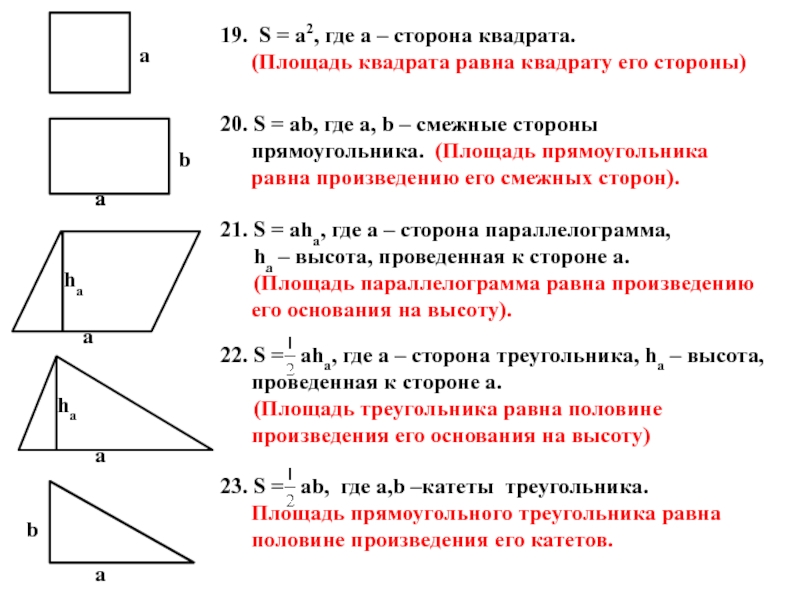
Слайд 919. S = a2, где a – сторона квадрата. (Площадь квадрата
20. S = ab, где a, b – смежные стороны прямоугольника. (Площадь прямоугольника равна произведению его смежных сторон).
21. S = aha, где a – сторона параллелограмма,
ha – высота, проведенная к стороне a.
(Площадь параллелограмма равна произведению его основания на высоту).
22. S = aha, где a – сторона треугольника, ha – высота, проведенная к стороне a.
(Площадь треугольника равна половине произведения его основания на высоту)
23. S = ab, где a,b –катеты треугольника. Площадь прямоугольного треугольника равна половине произведения его катетов.
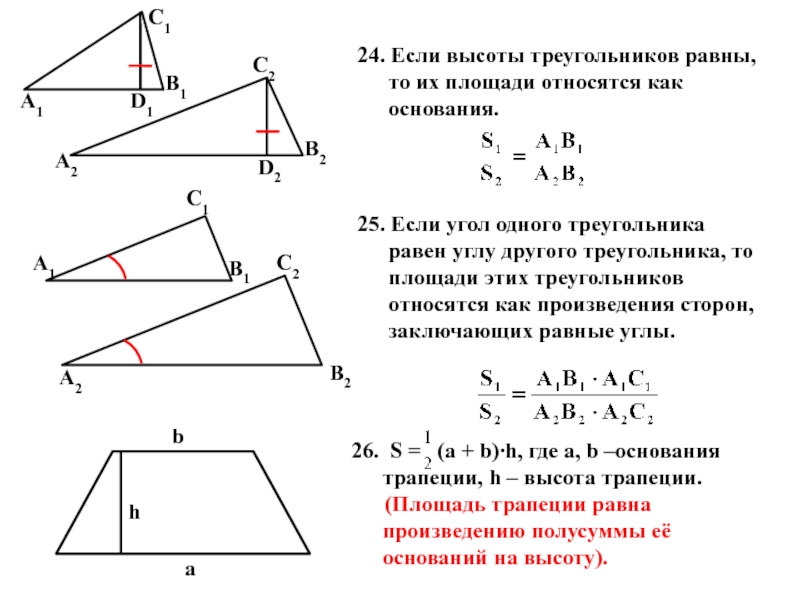
Слайд 1024. Если высоты треугольников равны, то их площади относятся как основания.
25.
26. S = (a + b)∙h, где a, b –основания трапеции, h – высота трапеции.
(Площадь трапеции равна произведению полусуммы её оснований на высоту).
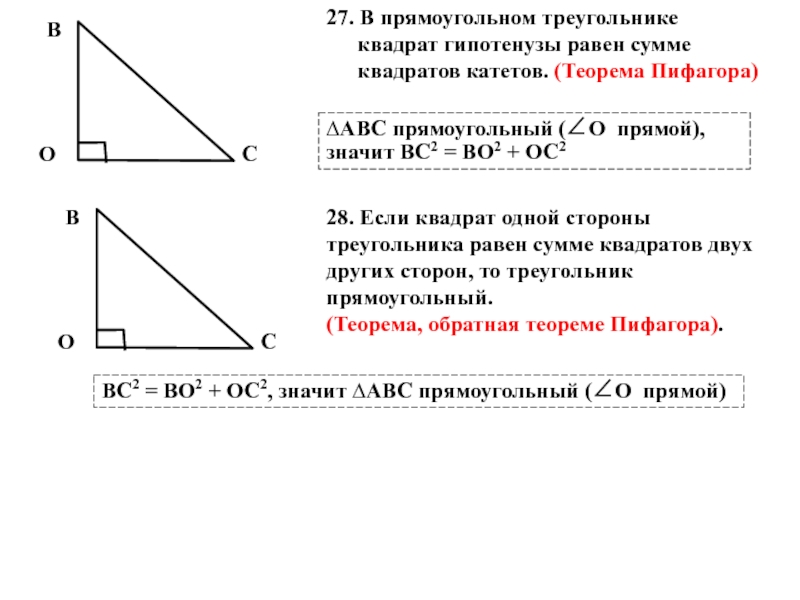
Слайд 11∆АВС прямоугольный (∠О прямой), значит ВС2 = ВО2 + ОС2
27. В
28. Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
(Теорема, обратная теореме Пифагора).
ВС2 = ВО2 + ОС2, значит ∆АВС прямоугольный (∠О прямой)
Слайд 12А
В
С
С1
В1
А1
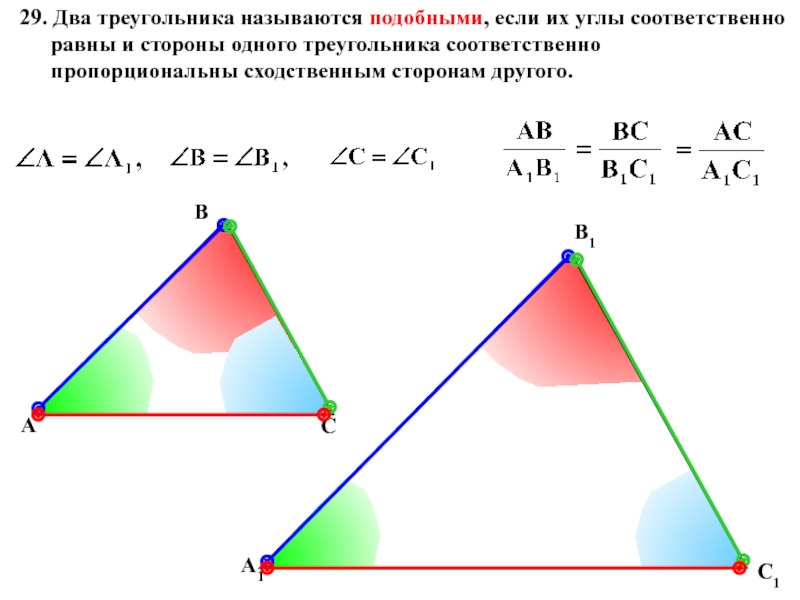
29. Два треугольника называются подобными, если их углы соответственно равны и
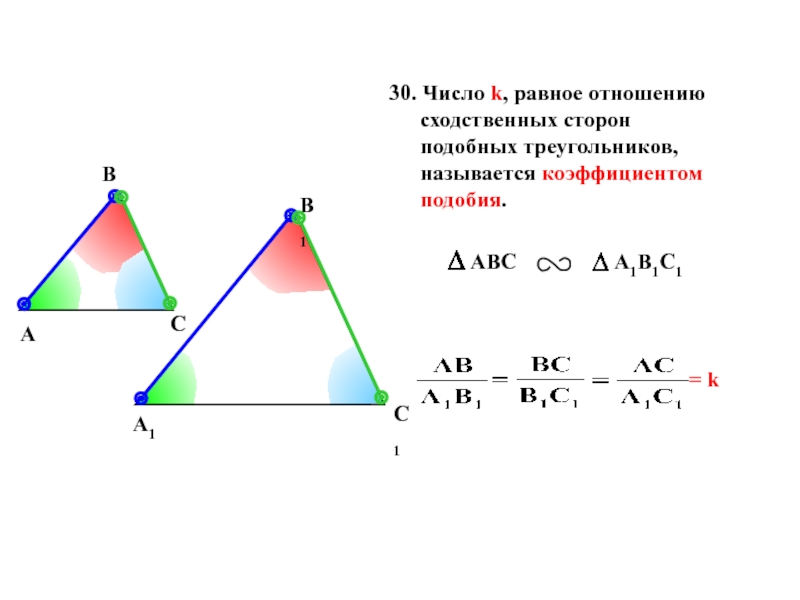
Слайд 1330. Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом
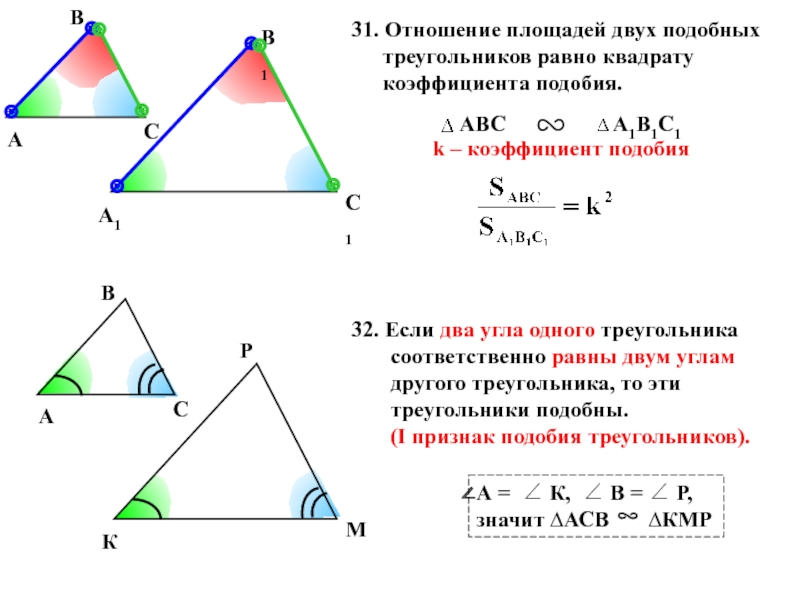
Слайд 1431. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
32. Если
(I признак подобия треугольников).
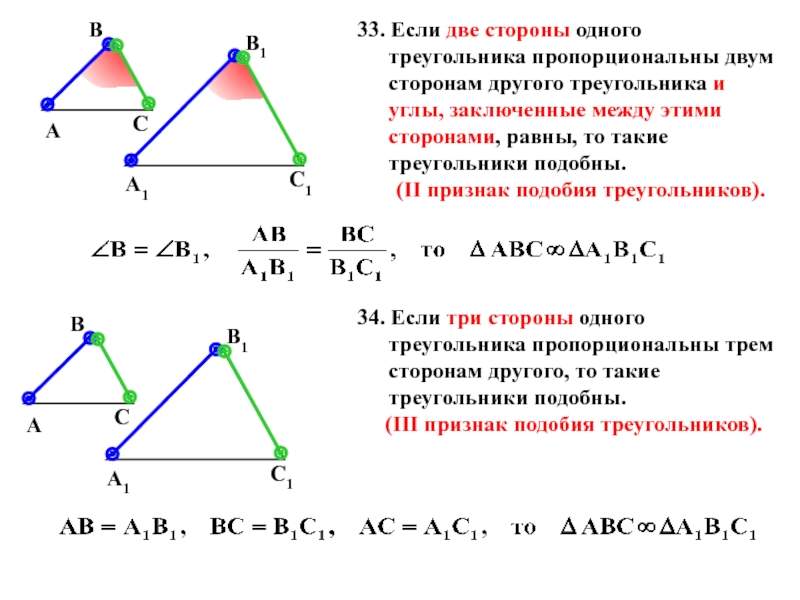
Слайд 1533. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника
(II признак подобия треугольников).
34. Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
(III признак подобия треугольников).
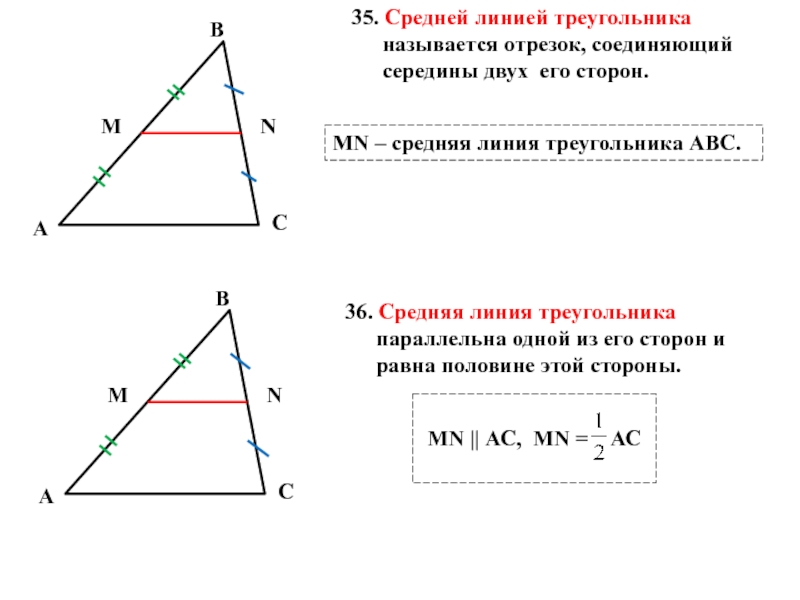
Слайд 1635. Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
МN
36. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Слайд 17N
M
F
P
K
S
O
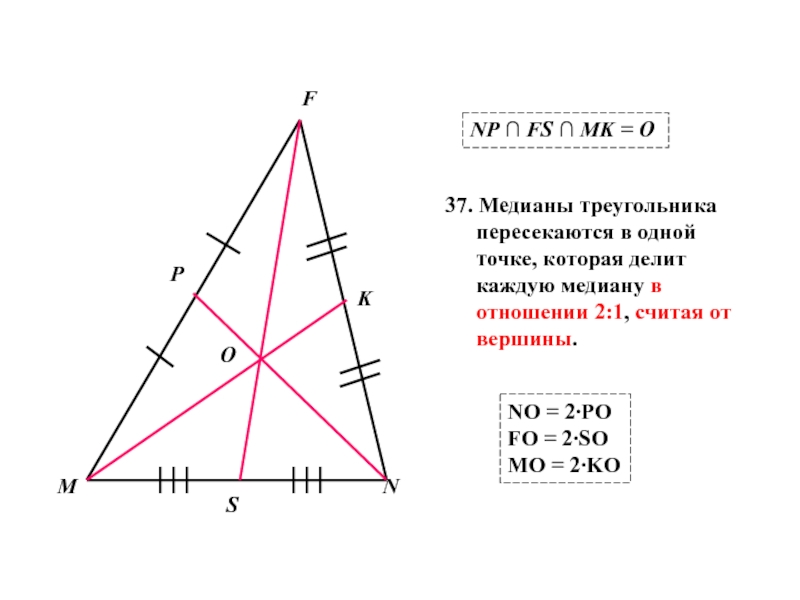
NP ∩ FS ∩ MK = O
37. Медианы треугольника пересекаются в
NO = 2∙PO
FO = 2∙SO
MO = 2∙KO
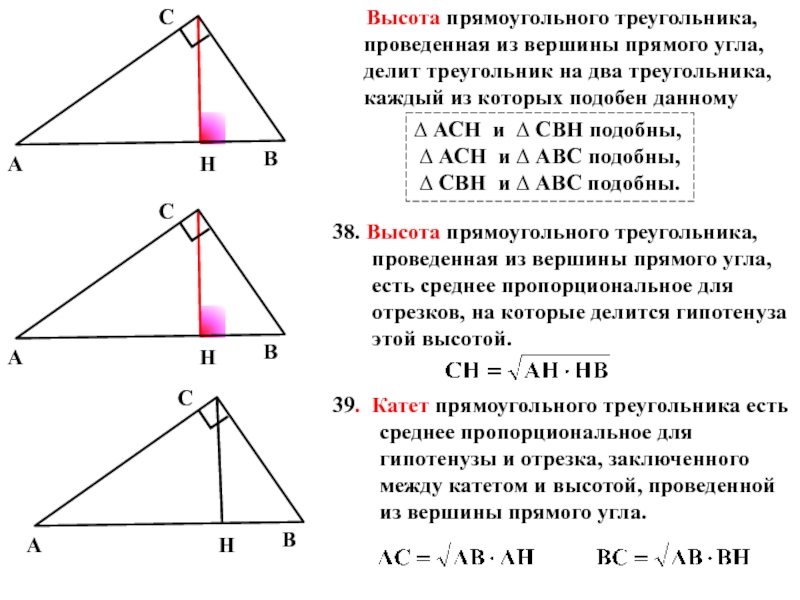
Слайд 18 Высота прямоугольного треугольника, проведенная из вершины прямого угла,
38. Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.
39. Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка, заключенного между катетом и высотой, проведенной из вершины прямого угла.
∆ АСН и ∆ СВН подобны,
∆ АСН и ∆ АВС подобны,
∆ СВН и ∆ АВС подобны.
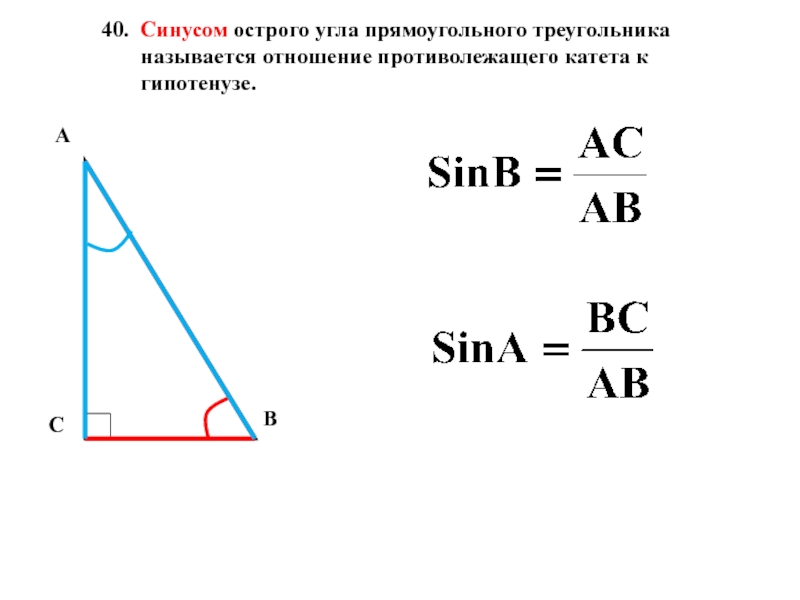
Слайд 1940. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета
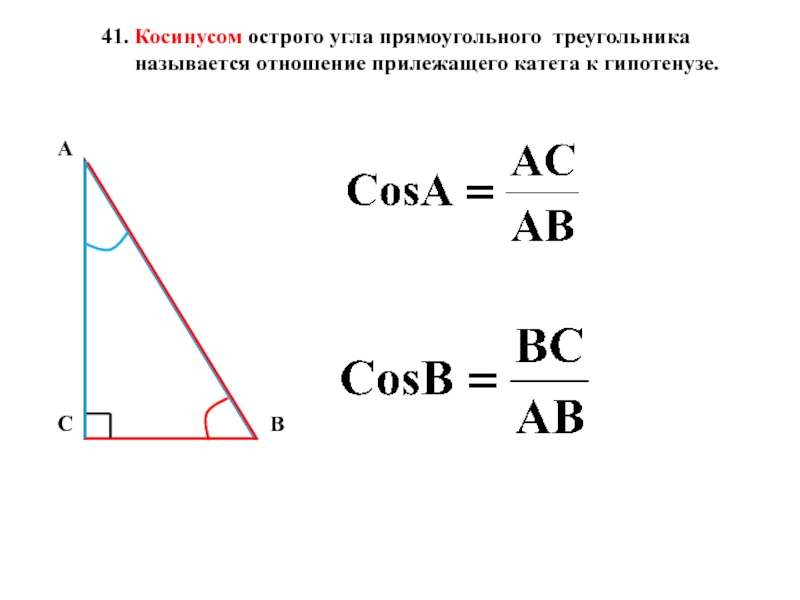
Слайд 2041. Косинусом острого угла прямоугольного треугольника
называется отношение прилежащего
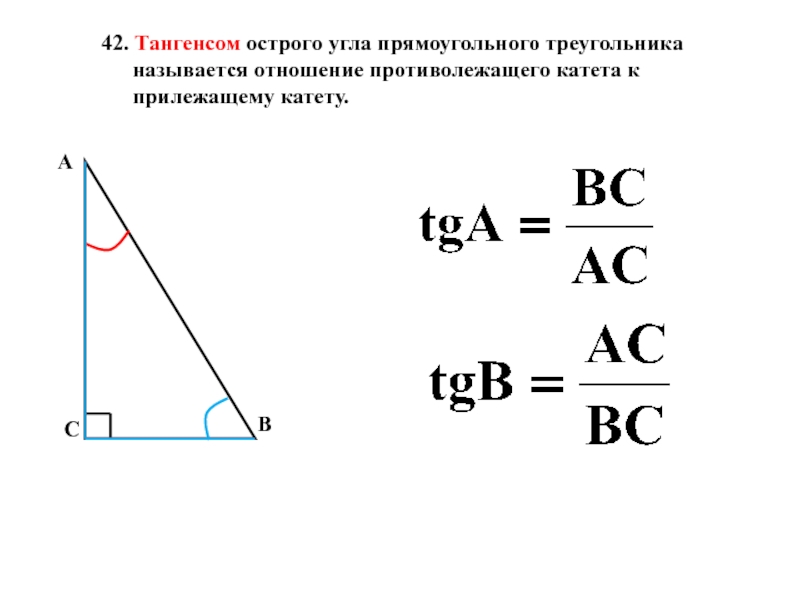
Слайд 2142. Тангенсом острого угла прямоугольного треугольника называется отношение
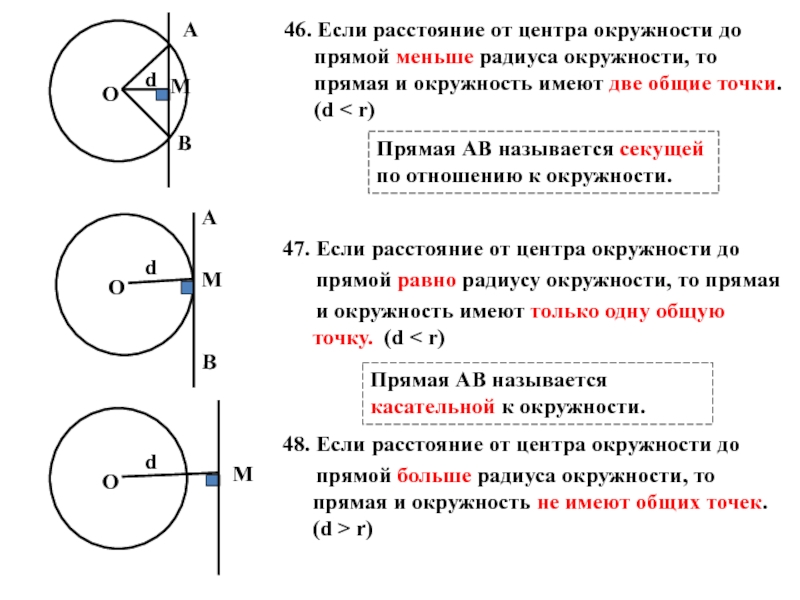
Слайд 2346. Если расстояние от центра окружности до прямой меньше радиуса окружности,
Прямая АВ называется секущей
по отношению к окружности.
47. Если расстояние от центра окружности до
прямой равно радиусу окружности, то прямая
и окружность имеют только одну общую точку. (d < r)
48. Если расстояние от центра окружности до
прямой больше радиуса окружности, то прямая и окружность не имеют общих точек. (d > r)
Прямая АВ называется касательной к окружности.
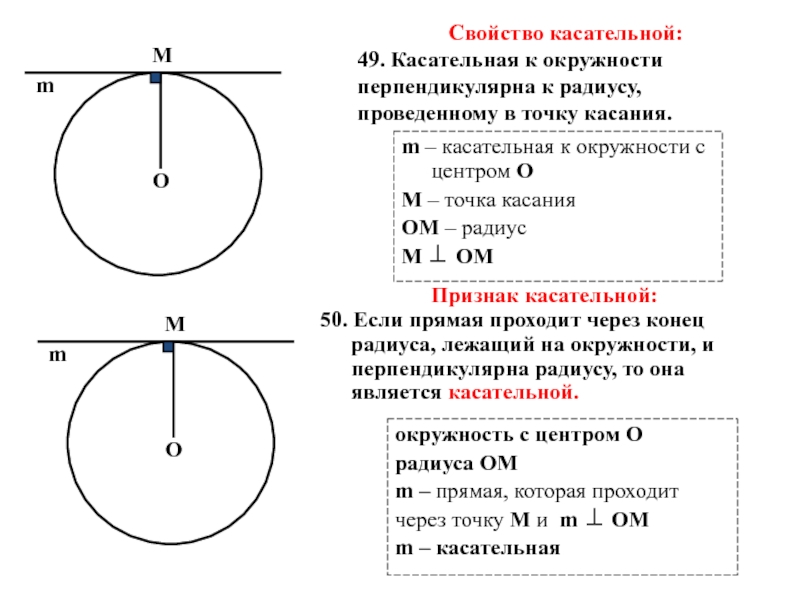
Слайд 24
m – касательная к окружности с центром О
М – точка касания
OM – радиус
M ⊥ ОМ
Признак касательной:
50. Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна радиусу, то она является касательной.
окружность с центром О
радиуса OM
m – прямая, которая проходит
через точку М и m ⊥ ОМ
m – касательная
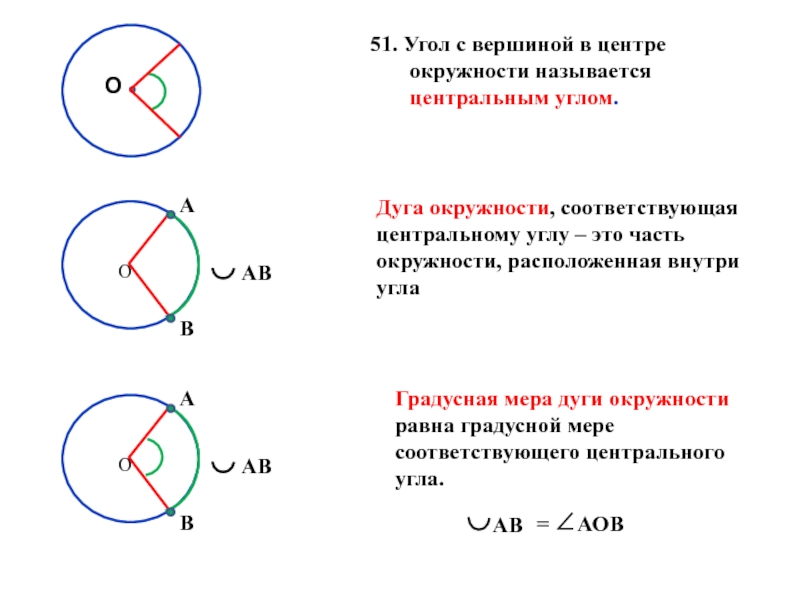
Слайд 2551. Угол с вершиной в центре окружности называется центральным углом.
Дуга
Градусная мера дуги окружности
равна градусной мере соответствующего центрального угла.
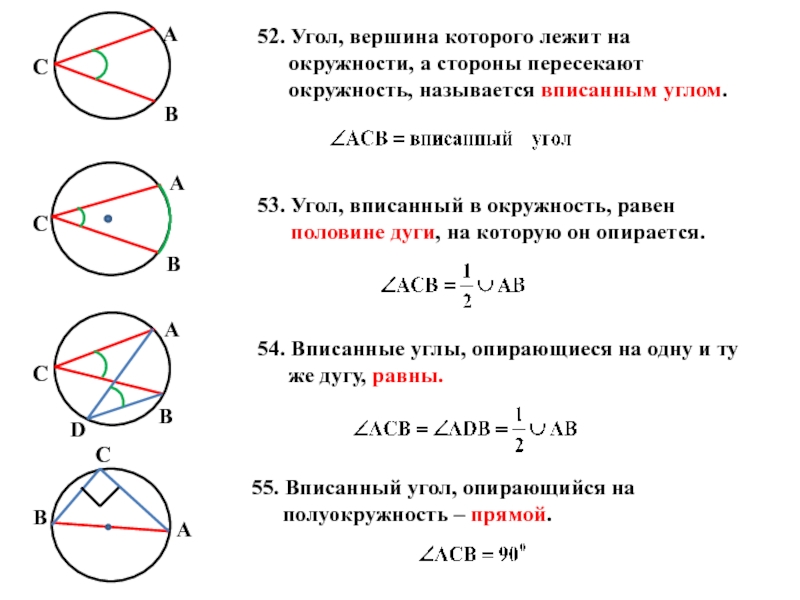
Слайд 2652. Угол, вершина которого лежит на окружности, а стороны пересекают окружность,
53. Угол, вписанный в окружность, равен
половине дуги, на которую он опирается.
54. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
55. Вписанный угол, опирающийся на полуокружность – прямой.
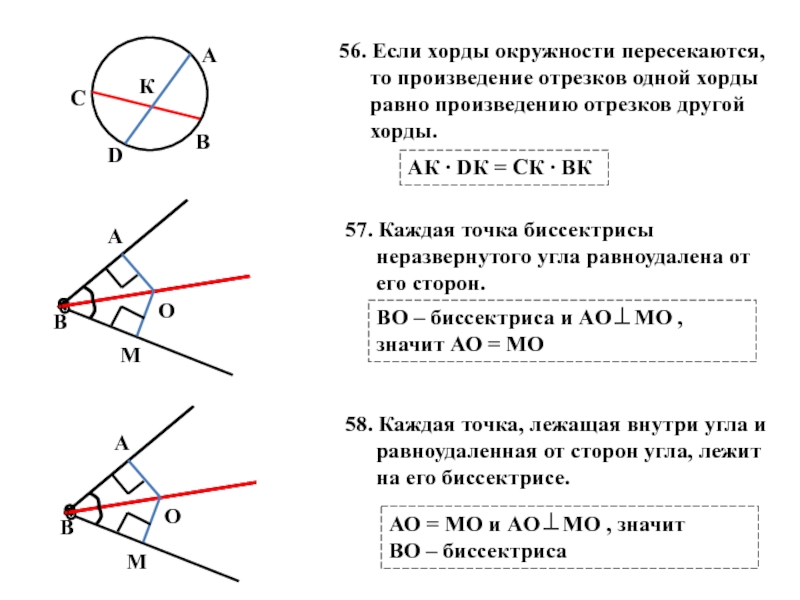
Слайд 2756. Если хорды окружности пересекаются, то произведение отрезков одной хорды равно
АК ∙ DК = СК ∙ ВК
57. Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.
58. Каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе.
ВО – биссектриса и AО⊥МО , значит АО = МО
АО = МО и AО⊥МО , значит
ВО – биссектриса
Слайд 28
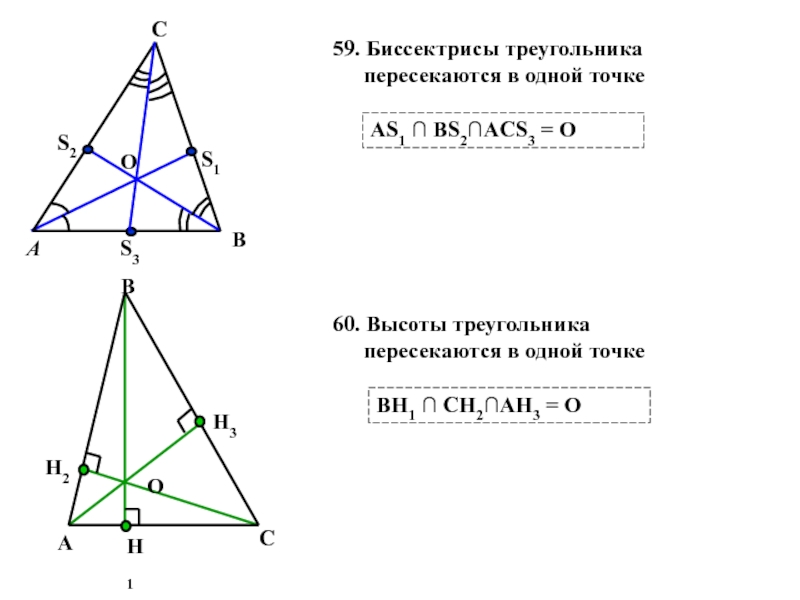
59. Биссектрисы треугольника пересекаются в одной точке
AS1 ∩ BS2∩АCS3 = О
60. Высоты треугольника пересекаются в одной точке
ВН1 ∩ СН2∩АН3 = О
Слайд 2961. Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного
m ⊥ AB и АО = ВО, значит m – серединный перпендикуляр
62. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
m – серединный перпендикуляр и С ϵ m, значит АС = ВС
63. Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
АС = ВС , значит m – серединный перпендикуляр
64 . Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
m, n, k – серединные перпендикуляры к сторонам треугольника, пересекаются в точке О
Слайд 3065. Если все стороны многоугольника касаются окружности, то окружность называется вписанной
АВСD – многоугольник описанный около окружности.
Окружность – вписана в многоугольник АВСD
66. В любой треугольник можно вписать окружность
67. В любом описанном четырехугольнике суммы противоположных сторон равны.
Четырехугольник АВСD описан около окружности, значит АВ + DС = АD + ВС
68. Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
АВ + DС = АD + ВС , значит в четырехугольник АВСD можно вписать окружность
Слайд 3169. Если все вершины многоугольника лежат на окружности, то окружность называется
70. Около любого треугольника можно описать окружность.
71.В любом вписанном четырехугольнике сумма противоположных углов равна 1800.
72. Если сумма противоположных углов четырехугольника равна 1800, то около него можно описать окружность.
АВСDE – многоугольник вписанный в окружность.
Окружность – описана около многоугольника АВСDЕ
Четырехугольник АВСD вписан в окружности, значит А + С = В + D = 1800
А + С = В + D = 1800 , значит около четырехугольника АВСD можно описать окружность
Слайд 32Федеральный компонент государственного образовательного стандарта основного общего образования по математике (пр.министерства
Авторская программа Атанасян Л.С., Бутузов В.Ф., Кодомцев С.Б. составитель БурмистроваТ.А., М. «Просвещение», 2015
УМК «Геометрия 7-9» Атанасян Л.С., Бутузов В.Ф.,и др- М.:Просвещение, 2015г
Интернет – ресурсы: http://le-savchen.uCoz.ru
Литература: