- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Симметрия в геометрии
Содержание
- 1. Презентация по математике на тему Симметрия в геометрии
- 2. ОпределениеСимметрия — слово греческого происхождения, как и
- 3. Центральная симметрия
- 4. Центральная симметрияСимметрию относительно точки называют центральной
- 5. Центральная симметрияПостроим треугольник A1B1C1, симметричный треугольнику
- 6. Осевая симметрия
- 7. Осевая симметрияОсевая симметрия — это симметрия
- 8. Осевая симметрияПостроим треугольник A1B1C1, симметричный треугольнику
- 9. Зеркальная симметрия
- 10. Зеркальная симметрияЗеркальной симметрией (симметрией относительно плоскости
- 11. Спасибо за внимание!!!
Слайд 2Определение
Симметрия — слово греческого происхождения, как и многие другие слова, которые
Люди с давних времён использовали симметрию в рисунках, орнаментах, предметах быта, в архитектуре, художестве, строительстве.
Но симметрия широко распространена и в природе, где не было вмешательства человеческой руки. Её можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных, в форме кристаллических тел, в порхающей бабочке, загадочной снежинке, морской звезде.
Слайд 4Центральная
симметрия
Симметрию относительно точки называют центральной симметрией.
Точки M и M1 симметричны
Точка O называется центром симметрии.
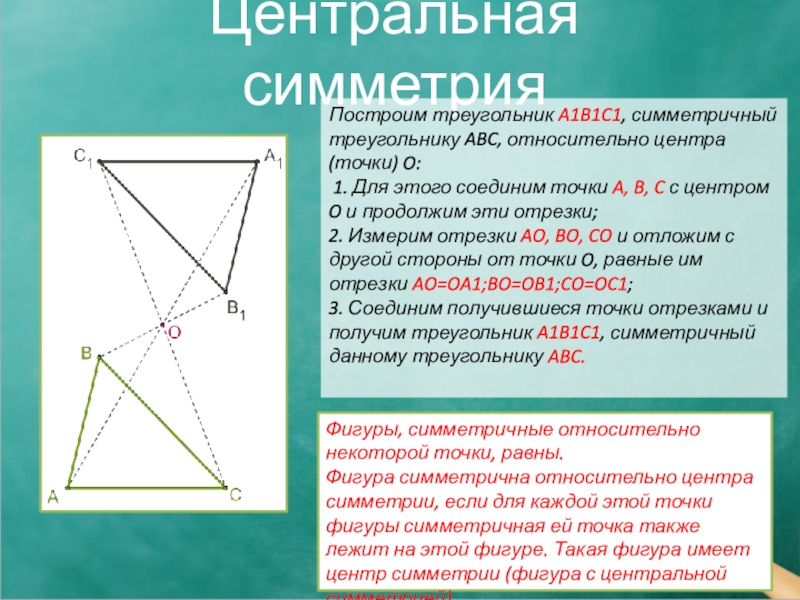
Слайд 5Центральная симметрия
Построим треугольник A1B1C1, симметричный треугольнику ABC, относительно центра (точки)
1. Для этого соединим точки A, B, C с центром O и продолжим эти отрезки;
2. Измерим отрезки AO, BO, CO и отложим с другой стороны от точки O, равные им отрезки AO=OA1;BO=OB1;CO=OC1;
3. Соединим получившиеся точки отрезками и получим треугольник A1B1C1, симметричный данному треугольнику ABC.
Фигуры, симметричные относительно некоторой точки, равны.
Фигура симметрична относительно центра симметрии, если для каждой этой точки фигуры симметричная ей точка также лежит на этой фигуре. Такая фигура имеет центр симметрии (фигура с центральной симметрией).
Слайд 7Осевая
симметрия
Осевая симметрия — это симметрия относительно проведённой прямой (оси).
Точки M
Слайд 8Осевая
симметрия
Построим треугольник A1B1C1, симметричный треугольнику ABC относительно красной прямой:
1.
2. Измерим расстояния от вершин треугольника до получившихся точек на прямой и отложим с другой стороны прямой такие же расстояния.
3. Соединим получившиеся точки отрезками и получим треугольник A1B1C1, симметричный данному треугольнику ABC.
Фигуры, симметричные относительно прямой, равны.
Фигура считается симметричной относительно прямой, если для каждой точки рассматриваемой фигуры, симметричная для неё точка относительно данной прямой также находится на этой фигуре. Прямая является в этом случае осью симметрии фигуры.
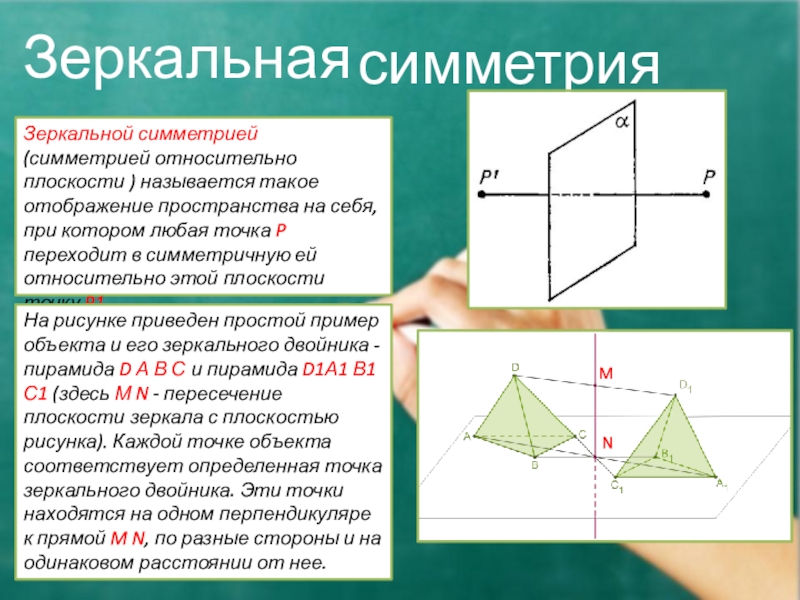
Слайд 10Зеркальная
симметрия
Зеркальной симметрией (симметрией относительно плоскости ) называется такое отображение пространства
На рисунке приведен простой пример объекта и его зеркального двойника - пирамида D А В С и пирамида D1А1 В1 С1 (здесь М N - пересечение плоскости зеркала с плоскостью рисунка). Каждой точке объекта соответствует определенная точка зеркального двойника. Эти точки находятся на одном перпендикуляре к прямой M N, по разные стороны и на одинаковом расстоянии от нее.
M
N