- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
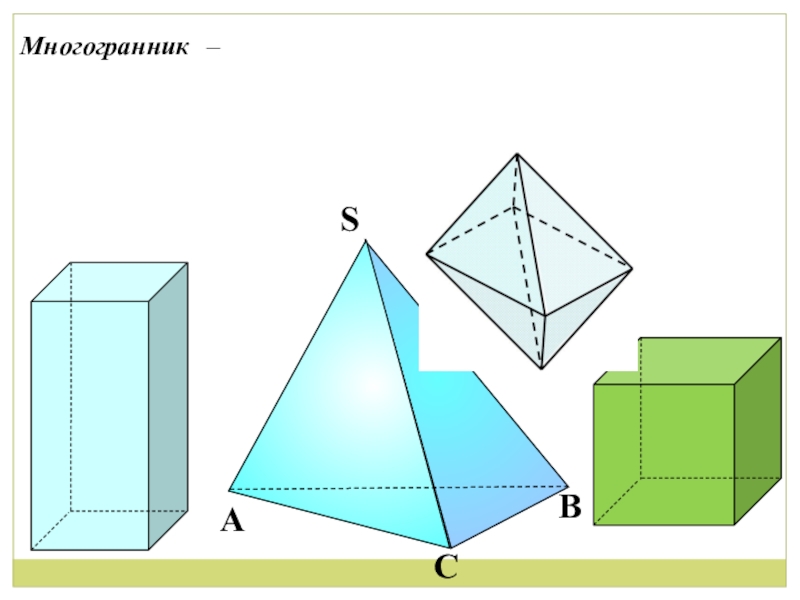
Презентация, доклад по математике на тему Призма (10 класс)
Содержание
- 1. Презентация по математике на тему Призма (10 класс)
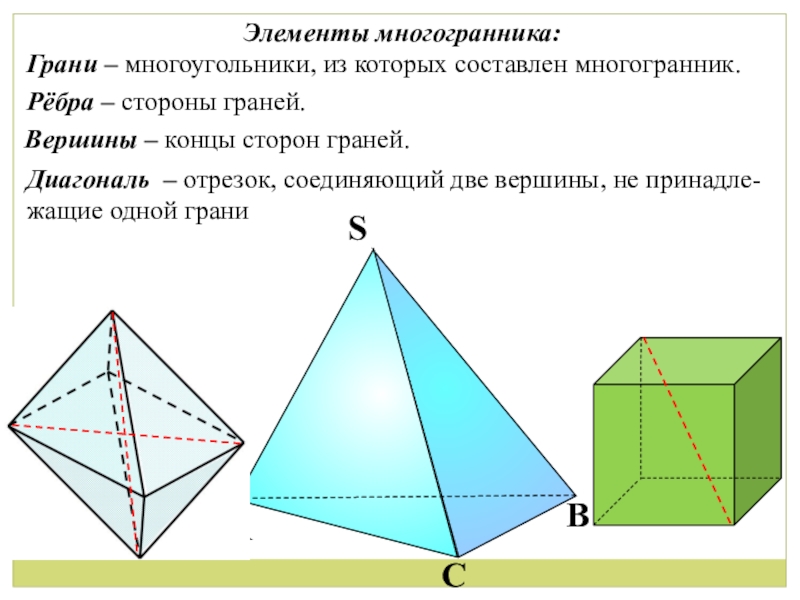
- 2. Элементы многогранника:Грани – многоугольники, из которых составлен
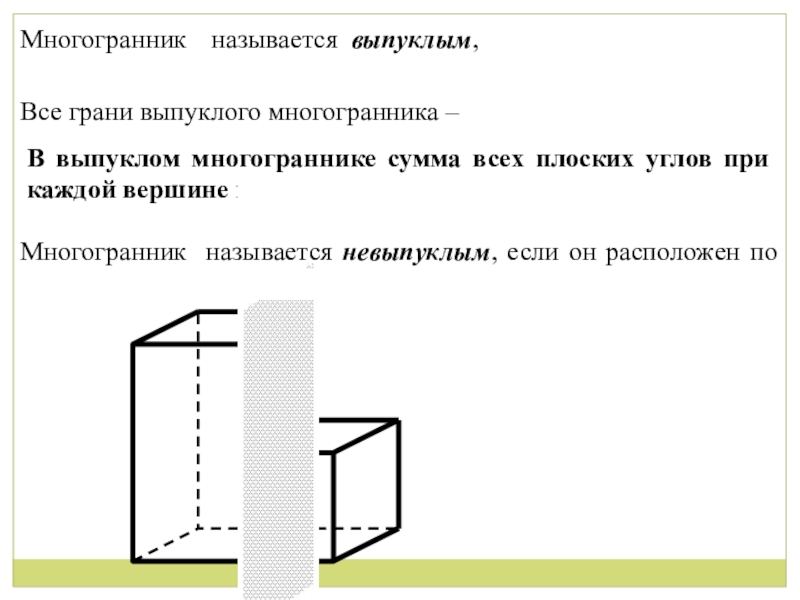
- 3. Многогранник называется выпуклым, если он расположен по
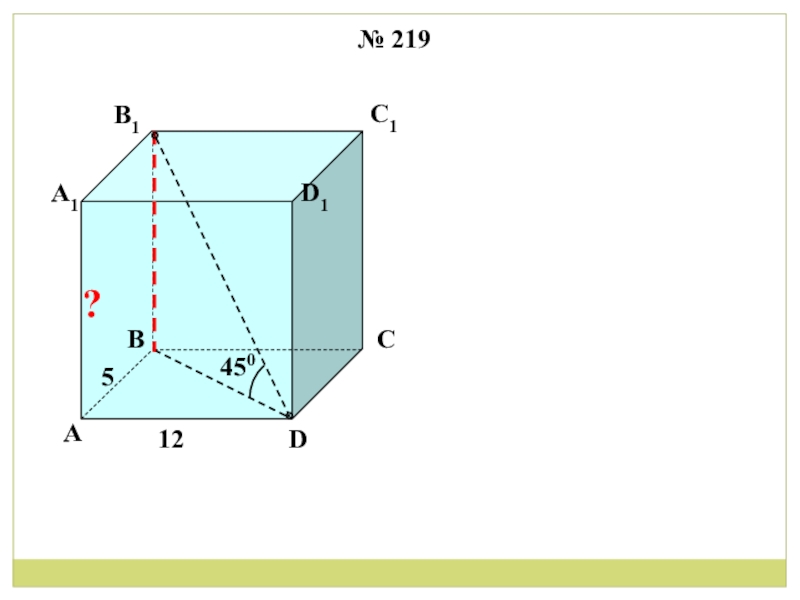
- 4. 125450АВDСА1В1D1С1№ 219?
- 5. Дома: п. 30 с. 60-61,с. 67 № 218 а), № 229 а)Призма
- 6. abРассмотрим два равных многоугольника А1А2…Аn и B1B2…Bn
- 7. А1А2АnB1Bn B2Равные многоугольники А1А2…Аn и B1B2…Bn называются
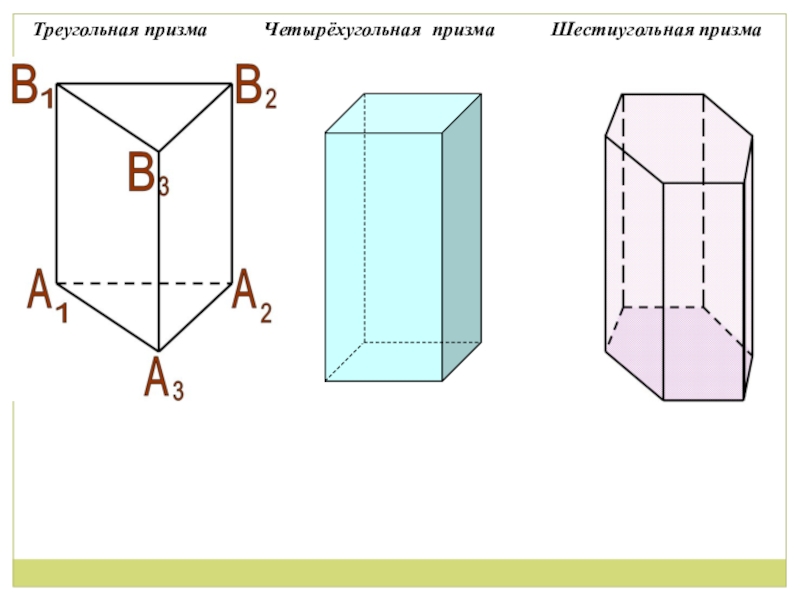
- 8. Треугольная призмаЧетырёхугольная призмаШестиугольная призма
- 9. Призма называется наклонной, если боковые рёбра призмы
- 10. Призма называется прямой, если боковые рёбра призмы
- 11. Теорема Площадь боковой поверхности прямой призмы равна
- 12. № 229 (б, г) с. 68В правильной
Слайд 2Элементы многогранника:
Грани – многоугольники, из которых составлен многогранник.
С
А
В
S
S
Рёбра – стороны граней.
Вершины
Диагональ – отрезок, соединяющий две вершины, не принадле-жащие одной грани
Слайд 3Многогранник называется выпуклым, если он расположен по одну сторону от плоскости
Все грани выпуклого многогранника – выпуклые многоугольники.
В выпуклом многограннике сумма всех плоских углов при каждой вершине меньше 360.
Многогранник называется невыпуклым, если он расположен по разные стороны от плоскости его граней.
Слайд 6a
b
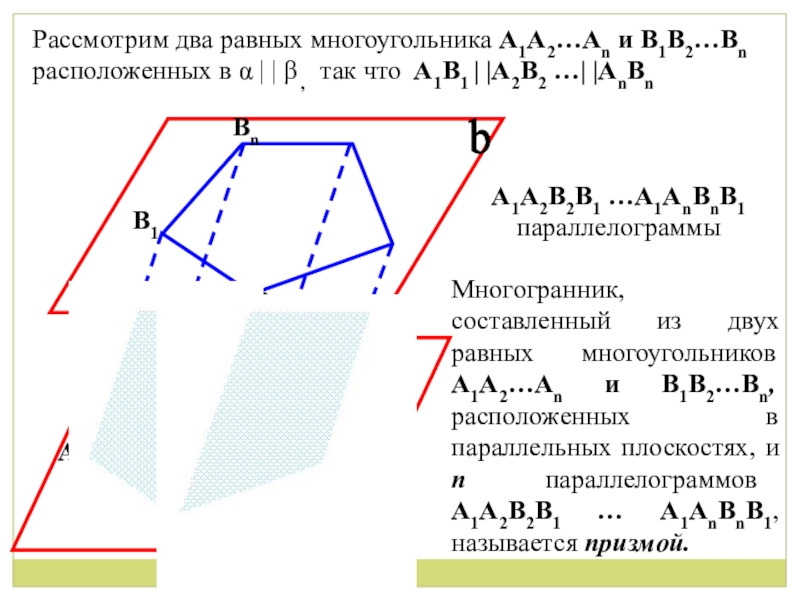
Рассмотрим два равных многоугольника А1А2…Аn и B1B2…Bn
расположенных в
А1
А2
Аn
B1
Bn
B2
так что
А1B1 А2B2 … АnBn
А1А2B2B1 …А1АnBnB1 параллелограммы
Многогранник, составленный из двух равных многоугольников А1А2…Аn и В1B2…Bn, расположенных в параллельных плоскостях, и п параллелограммов А1А2B2B1 … А1АnBnB1, называется призмой.
Слайд 7А1
А2
Аn
B1
Bn
B2
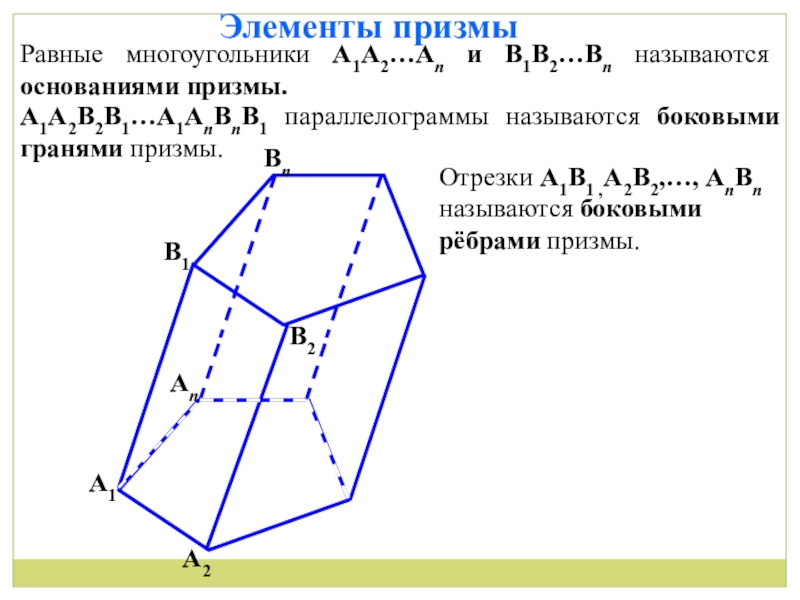
Равные многоугольники А1А2…Аn и B1B2…Bn называются основаниями призмы.
А1А2B2B1…А1АnBnB1 параллелограммы называются
Отрезки А1B1 ,А2B2,…, АnBn называются боковыми рёбрами призмы.
Элементы призмы
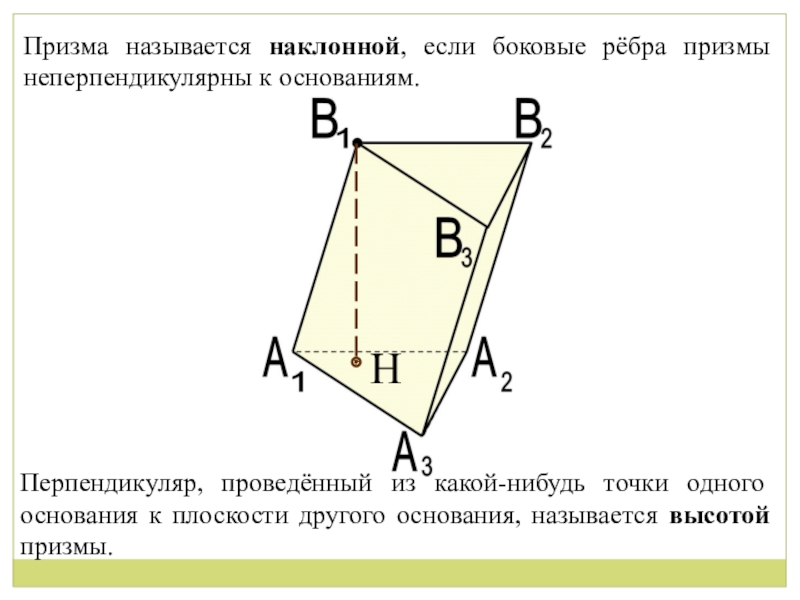
Слайд 9Призма называется наклонной, если боковые рёбра призмы неперпендикулярны к основаниям.
Перпендикуляр, проведённый
Н
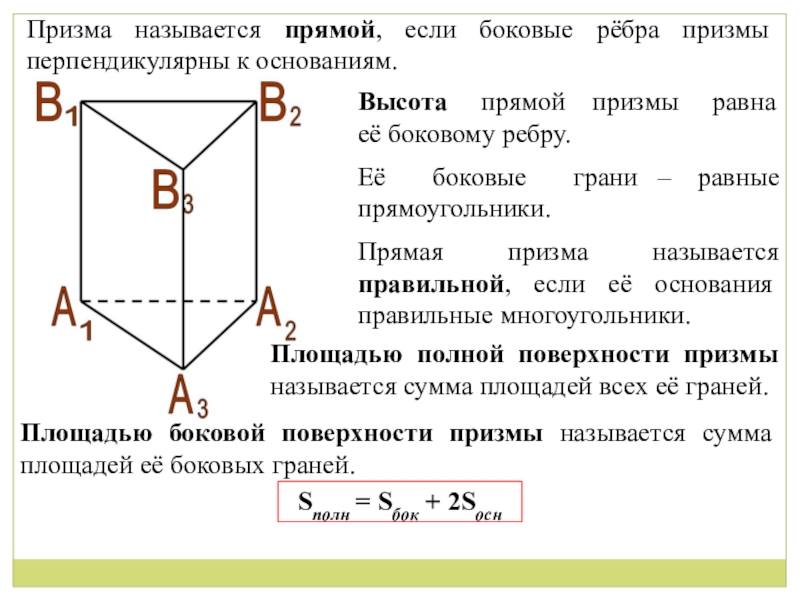
Слайд 10Призма называется прямой, если боковые рёбра призмы перпендикулярны к основаниям.
Высота
её боковому ребру.
Прямая призма называется правильной, если её основания правильные многоугольники.
Её боковые грани – равные
прямоугольники.
Площадью полной поверхности призмы называется сумма площадей всех её граней.
Площадью боковой поверхности призмы называется сумма площадей её боковых граней.
Sполн = Sбок + 2Sосн
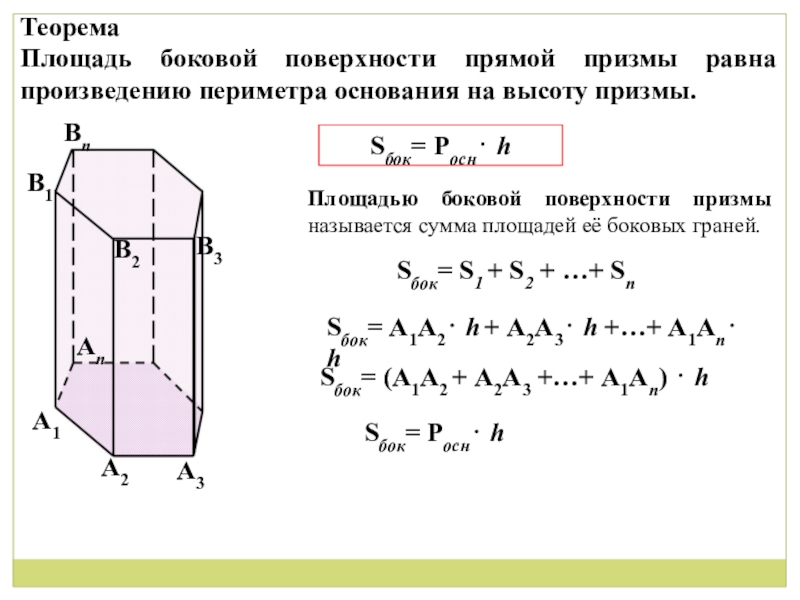
Слайд 11Теорема
Площадь боковой поверхности прямой призмы равна произведению периметра основания на
Площадью боковой поверхности призмы называется сумма площадей её боковых граней.
Sбок= Росн h
Sбок= S1 + S2 + …+ Sn
Sбок= А1А2 h + А2А3 h +…+ А1Аn h
Sбок= (А1А2 + А2А3 +…+ А1Аn) h
Sбок= Росн h
А1
А2
Аn
А3
В1
В2
В3
Вn
Слайд 12№ 229 (б, г) с. 68
В правильной n-угольной призме сторона основания
в) n = 6, а = 23 см, h = 5 дм.
Sполн = Sбок + 2Sосн
Sбок= Росн h
23
23
23
600