- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Призма
Содержание
- 1. Презентация по математике на тему Призма
- 2. Призмой называется многогранник, который состоит из двух
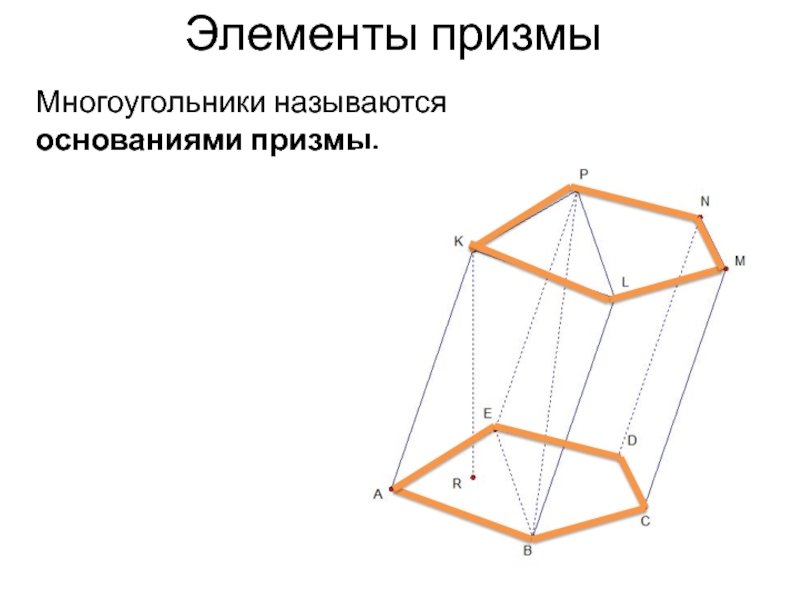
- 3. Многоугольники называются основаниями призмы.Элементы призмы
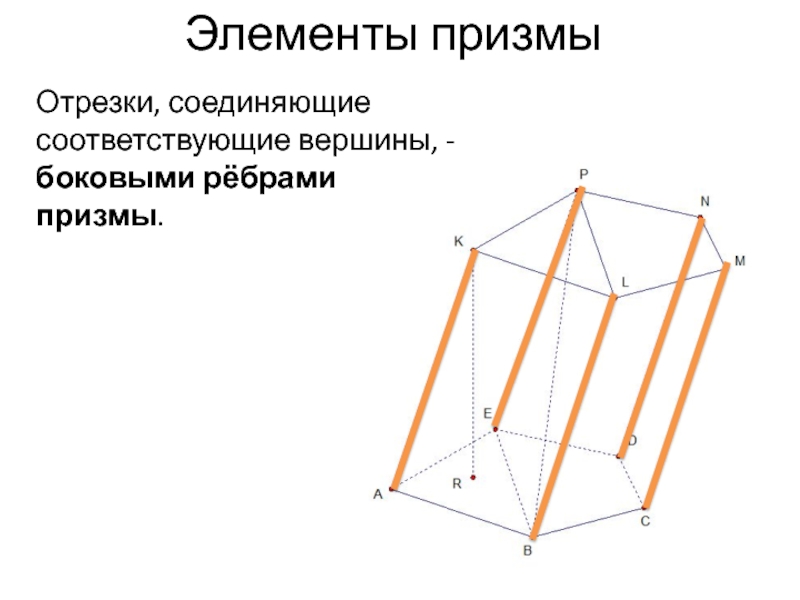
- 4. Отрезки, соединяющие соответствующие вершины, -боковыми рёбрами призмы.Элементы призмы
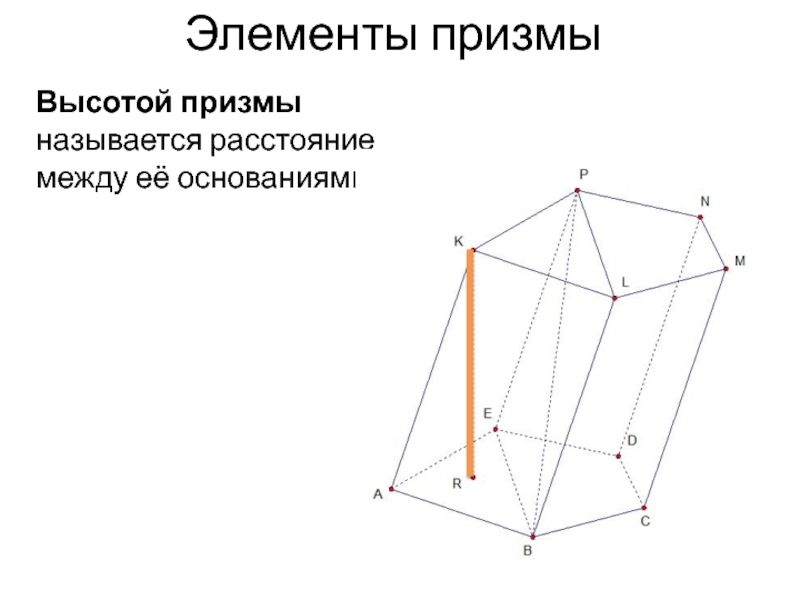
- 5. Высотой призмы называется расстояние между её основаниями.Элементы призмы
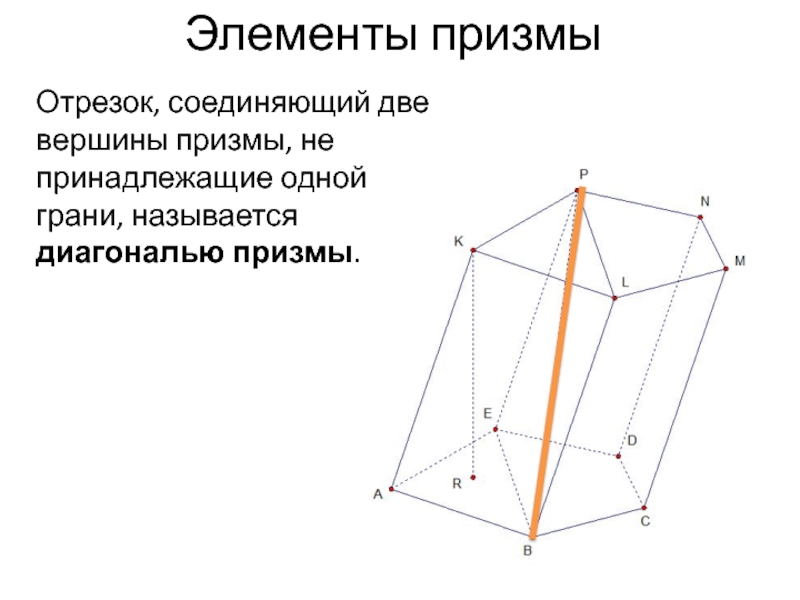
- 6. Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, называется диагональю призмы.Элементы призмы
- 7. Элементы призмыБоковой гранью призмы называются все грани,
- 8. Свойства призмыОснования призмы равны.Основания призмы лежат в
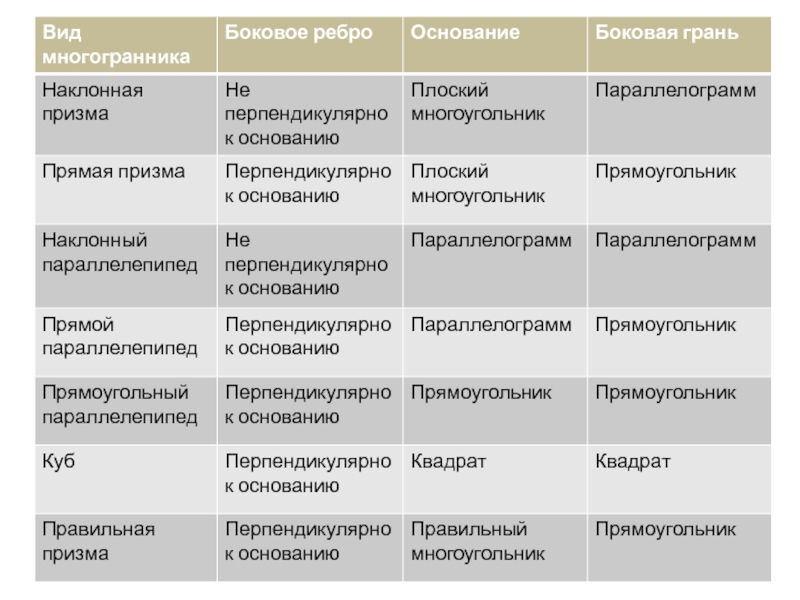
- 9. Виды призмПризма называется прямой, если её боковые рёбра перпендикулярны основаниям.В противном случае призма называется наклонной.
- 10. Виды призмПараллелепи́пед — призма, основанием которой служит параллелограмм,
- 11. Виды призмПрямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом.
- 12. Виды призмКуб (частный случай параллелепипеда и призмы)— правильный многогранник, каждая грань которого представляет собой квадрат.
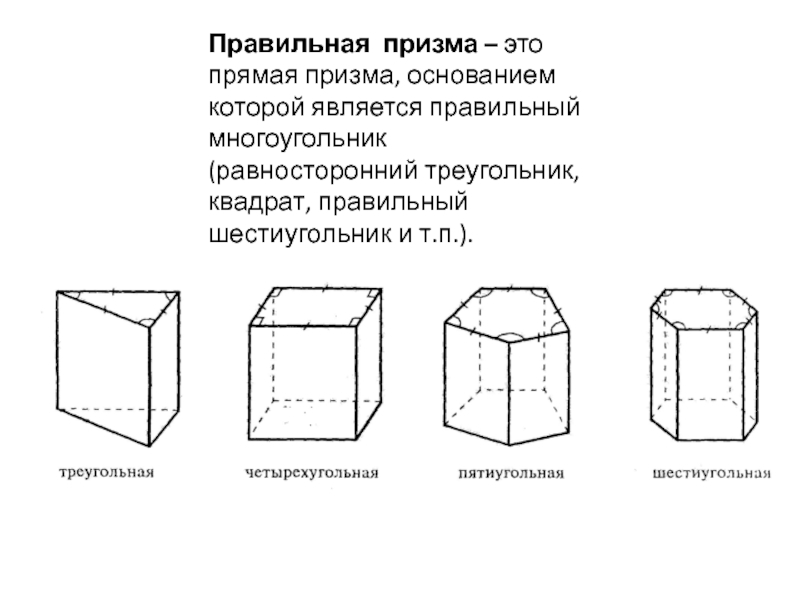
- 13. Правильная призма – это прямая призма, основанием
- 14. Слайд 14
Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников.Определение призмы
Слайд 2Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в
разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников.
Определение призмы
Слайд 6Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, называется диагональю
призмы.
Элементы призмы
Слайд 7Элементы призмы
Боковой гранью призмы называются все грани, кроме её оснований.
Боковой поверхностью
призмы (точнее боковой поверхности) называется сумма площадей боковых граней.
Полная поверхность призмы равна сумме поверхности и площадей оснований.
Полная поверхность призмы равна сумме поверхности и площадей оснований.
Слайд 8Свойства призмы
Основания призмы равны.
Основания призмы лежат в параллельных плоскостях.
Боковые ребра призмы
параллельны и равны.
У параллелепипеда противолежащие грани равны и параллельны.
Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
Площадь боковой поверхности призмы S=Pl, где — P периметр основания, l — высота призмы (длина бокового ребра).
Точка пересечения диагоналей параллелепипеда является центром симметрии.
В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трёх его измерений.
У параллелепипеда противолежащие грани равны и параллельны.
Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
Площадь боковой поверхности призмы S=Pl, где — P периметр основания, l — высота призмы (длина бокового ребра).
Точка пересечения диагоналей параллелепипеда является центром симметрии.
В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трёх его измерений.
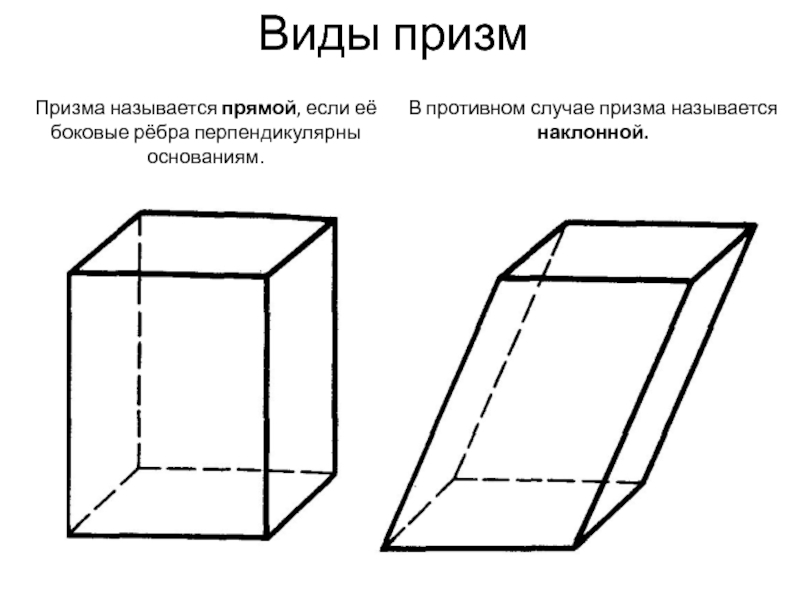
Слайд 9Виды призм
Призма называется прямой, если её боковые рёбра перпендикулярны основаниям.
В противном
случае призма называется наклонной.
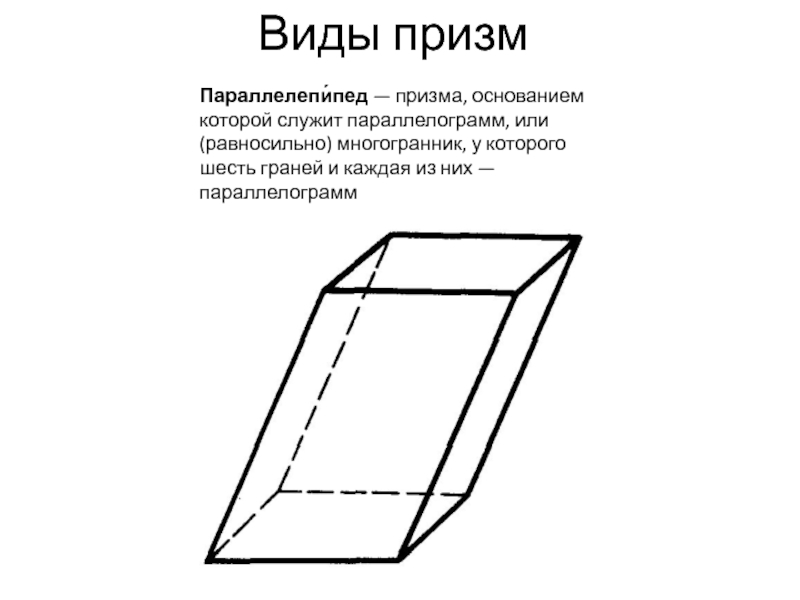
Слайд 10Виды призм
Параллелепи́пед — призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у
которого шесть граней и каждая из них — параллелограмм
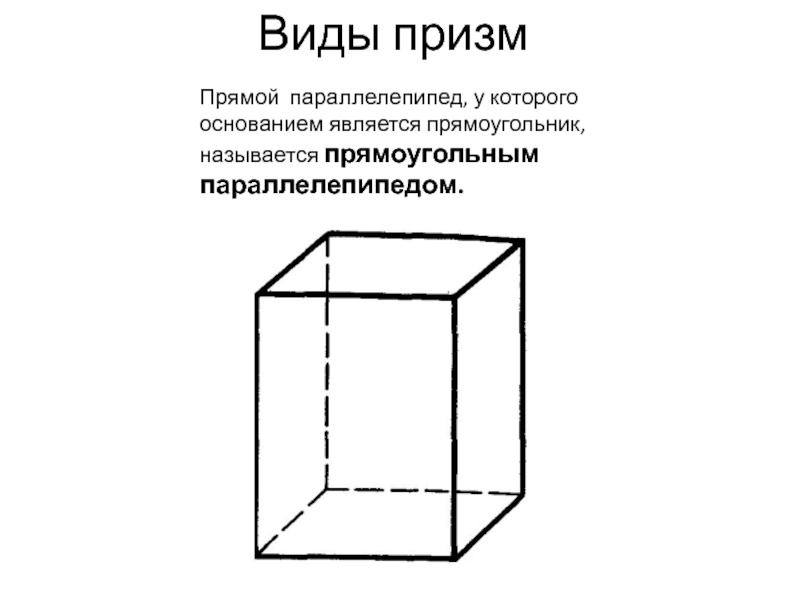
Слайд 11Виды призм
Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом.
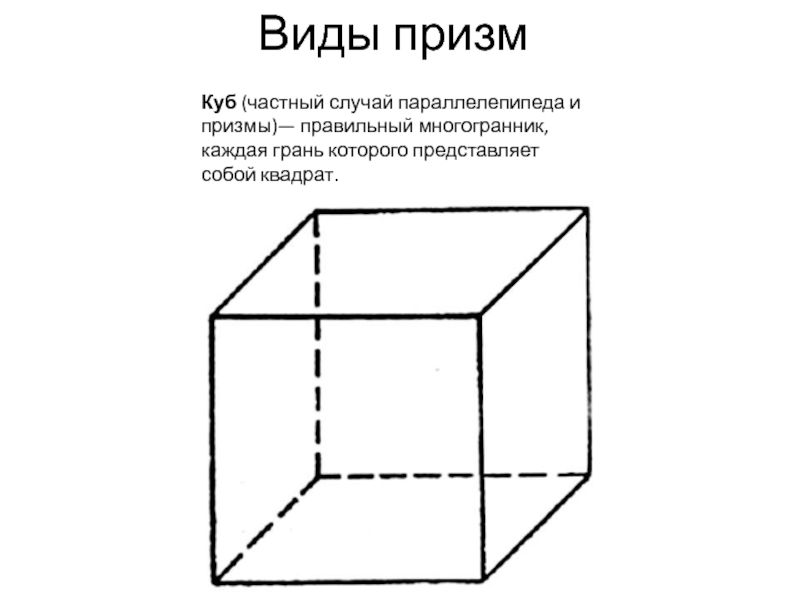
Слайд 12Виды призм
Куб (частный случай параллелепипеда и призмы)— правильный многогранник, каждая грань
которого представляет собой квадрат.
Слайд 13Правильная призма – это прямая призма, основанием которой является правильный многоугольник
(равносторонний треугольник, квадрат, правильный шестиугольник и т.п.).