- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему :Правильные многогранники
Содержание
- 1. Презентация по математике на тему :Правильные многогранники
- 2. Общие сведения и определениеВ трёхмерном пространстве правильным
- 3. Историческое происхождениеПравильные многогранники интересовали многих великих учёных.
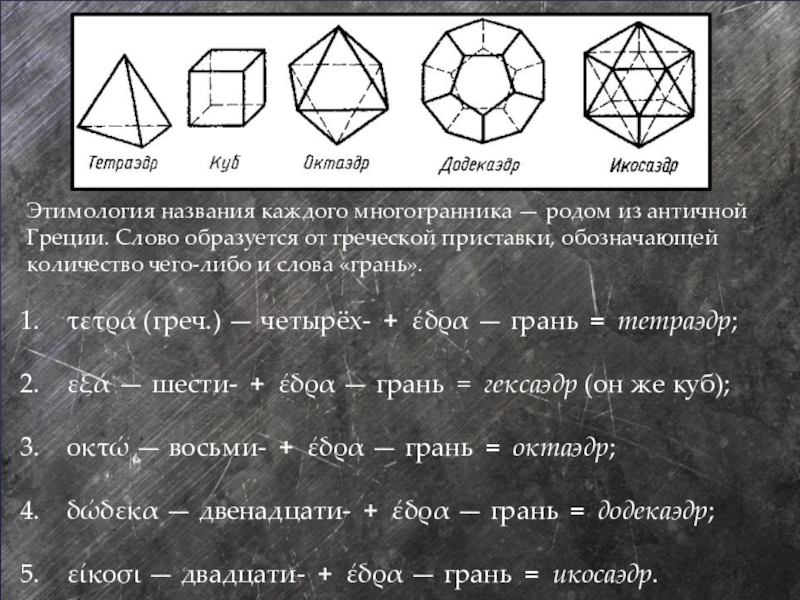
- 4. Этимология названия каждого многогранника — родом из
- 5. Комбинаторные свойства и общие формулыЭйлер вывел формулу, связывающую
- 6. Отдельно стоит оговорить символы Шлефли {p, q}:p — число рёбер
- 7. #1 Правильный тетраэдрНе всякий тетраэдр по определению
- 8. Формулы правильного тетраэдраУ тетраэдра 4 грани, 4
- 9. Тетраэдр в молекулярном миреТетраэдр в архитектуреКонструкция тетраэдрической
- 10. #2 Куб (правильный гексаэдр)ABCDКуб — правильный многогранник,
- 11. Формулы кубаУ куба 6 граней, 8 вершин
- 12. Кубик РубикаИгральные костиКубическая форма игральных костей регулирует
- 13. #3 Правильный октаэдрABCDHH1Октаэдр является правильным, если его грани —
- 14. Формулы правильного октаэдраУ октаэдра 8 граней, 6
- 15. В природе многие кубические кристаллы имеют форму октаэдра: алмаз, сульфат
- 16. #4 Правильный додекаэдрДодекаэдр составлен из двенадцати правильных пятиугольников,
- 17. Формулы додекаэдраУ додекаэдра 12 граней, 20 вершин
- 18. Интересно, что форму, близкую к додекаэдру, имеет
- 19. #5 Правильный икосаэдрBACDEFGKMHPLИкосаэдр — правильный многогранник, который составлен из
- 20. Формулы икосаэдраУ додекаэдра 20 граней, 12 вершин
- 21. Микроорганизмы в виде икосаэдраБактериофагМимивирусДанные виды микроорганизмов являются вирусами.
- 22. Подведём итоги услышанногоФорма «вопрос-ответ»:Как звали учёного, который
- 23. Подведём итоги услышанногоФорма «вопрос-ответ»:Как звали учёного, который
- 24. Спасибо за внимание! ( неспасибо за невнимание)
Слайд 2Общие сведения и определение
В трёхмерном пространстве правильным многогранником называется выпуклый многогранник,
Многогранник называется правильным, если:
он выпуклый;
все его грани являются равными правильными многоугольниками;
в каждой его вершине сходится одинаковое число рёбер.
Слайд 3Историческое происхождение
Правильные многогранники интересовали многих великих учёных. И этот интерес выходил
Возможно, именно красота и гармония правильных многогранников заставляла великих учёных прошлого видеть их назначение более масштабным, чем просто геометрических объектов.
В трёхмерном пространстве существует ровно пять правильных многогранников: тетраэдр, октаэдр, куб (гексаэдр), икосаэдр, додекаэдр.
То, что других правильных многогранников не существует, было доказано Евклидом (около 300 г. до н.э.) в его великих Началах. Евклид также нашёл для каждого правильного многогранника отношение диаметра описанной сферы к длине ребра.
Слайд 4Этимология названия каждого многогранника — родом из античной Греции. Слово образуется
τετρά (греч.) — четырёх- + έδρα — грань = тетраэдр;
εξά — шести- + έδρα — грань = гексаэдр (он же куб);
οκτώ — восьми- + έδρα — грань = октаэдр;
δώδεκα — двенадцати- + έδρα — грань = додекаэдр;
είκοσι — двадцати- + έδρα — грань = икосаэдр.
Слайд 5Комбинаторные свойства и общие формулы
Эйлер вывел формулу, связывающую число вершин (В), граней
В + Г = Р + 2
Отношение количества вершин правильного многогранника к количеству рёбер одной его грани равно отношению количества граней этого же многогранника к количеству рёбер, выходящих из одной его вершины. У тетраэдра это отношение равно 4:3, у гексаэдра и октаэдра — 2:1, а у додекаэдра и икосаэдра — 4:1
Слайд 6Отдельно стоит оговорить символы Шлефли {p, q}:
p — число рёбер в каждой грани;
q — число
Важной комбинаторной характеристикой многогранника, которую можно выразить через числа p и q, является общее количество вершин (В), рёбер (Р) и граней (Г). Постольку поскольку любое ребро соединяет две вершины и лежит между двумя гранями, выполняется соотношение:
Из этих соотношений и формулы Эйлера можно получить следующие выражения для В, Р и Г:
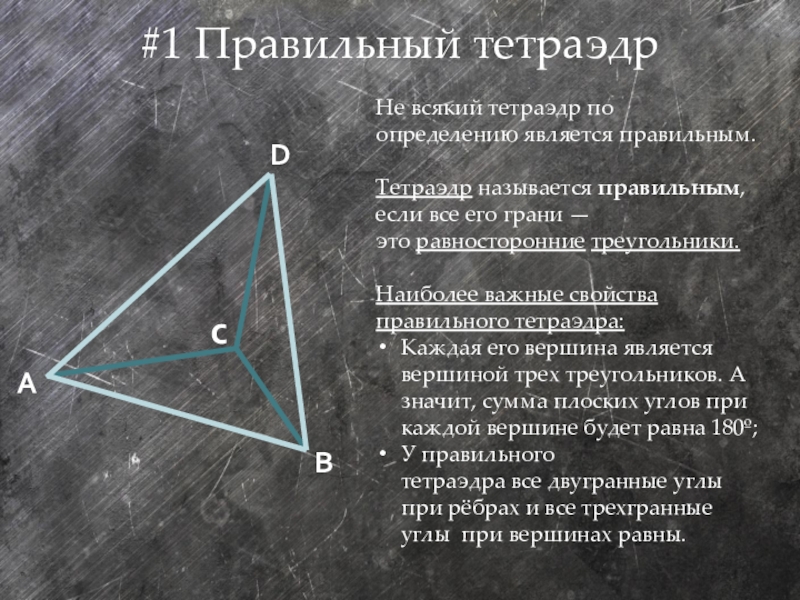
Слайд 7#1 Правильный тетраэдр
Не всякий тетраэдр по определению является правильным.
Тетраэдр называется правильным, если все
Наиболее важные свойства правильного тетраэдра:
Каждая его вершина является вершиной трех треугольников. А значит, сумма плоских углов при каждой вершине будет равна 180º;
У правильного тетраэдра все двугранные углы при рёбрах и все трехгранные углы при вершинах равны.
А
B
c
D
Слайд 8Формулы правильного тетраэдра
У тетраэдра 4 грани, 4 вершины и 6 ребер.
Площадь одной грани тетраэдра
Площадь поверхности правильного тетраэдра
Объем правильного тетраэдра
Высота, опущенная на основание
Радиус вписанной в тетраэдр окружности
Радиус описанной окружности
Слайд 9Тетраэдр в молекулярном мире
Тетраэдр в архитектуре
Конструкция тетраэдрической формы образует жёсткую, статически
Молекула метана
Тетраэдр
пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм, мостов и т. д. Стержни испытывают только продольные нагрузки.
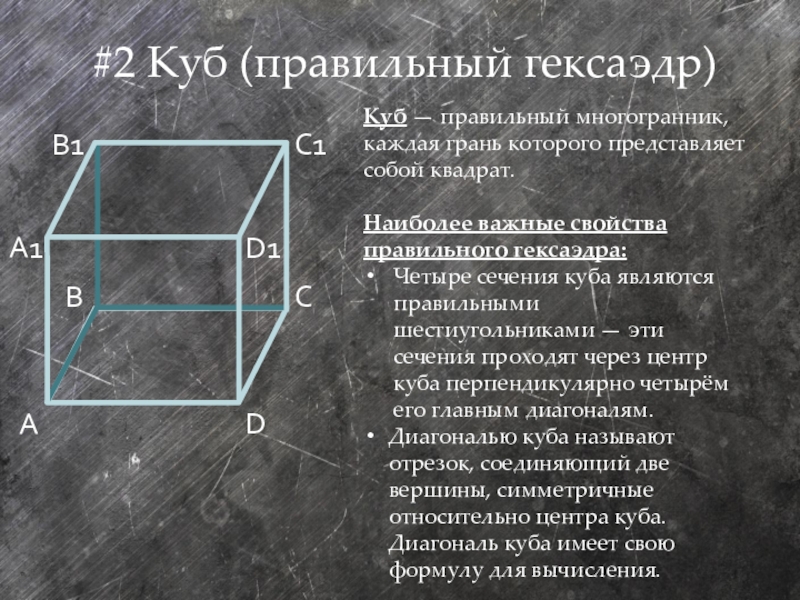
Слайд 10#2 Куб (правильный гексаэдр)
A
B
C
D
Куб — правильный многогранник, каждая грань которого представляет
Наиболее важные свойства правильного гексаэдра:
Четыре сечения куба являются правильными шестиугольниками — эти сечения проходят через центр куба перпендикулярно четырём его главным диагоналям.
Диагональю куба называют отрезок, соединяющий две вершины, симметричные относительно центра куба. Диагональ куба имеет свою формулу для вычисления.
A1
B1
C1
D1
Слайд 11Формулы куба
У куба 6 граней, 8 вершин и 12 ребер.
Для
Площадь одной грани куба
Площадь поверхности куба
Объем куба
Диагональ квадрата (грани) куба
Диагональ куба
Слайд 12Кубик Рубика
Игральные кости
Кубическая форма игральных костей регулирует справедливость вероятности выпадения того
Структура трёхмерного пространства такова, что любой прямоугольный параллелепипед условно разбиваем на равные друг другу меньшие по размеру кубы, которые, в свою очередь, разбиваются на более меньшие.
В компьютерной 3D-анимации (трехмерная графика в видеоиграх и компьютерных анимационных фильмах) первоначальной единицей моделирования пространства является куб.
Приобрела широкое распространение (в отличие от формы других правильных многогранников) вследствие своей простоты.
Слайд 13#3 Правильный октаэдр
A
B
C
D
H
H1
Октаэдр является правильным, если его грани — восемь равносторонних треугольников.
Из определения
Октаэдр можно вписать в тетраэдр, притом четыре из восьми граней октаэдра будут совмещены с четырьмя гранями тетраэдра, все шесть вершин октаэдра будут совмещены с центрами шести ребер тетраэдра.
Октаэдр можно вписать в куб, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.
В октаэдр можно вписать куб, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра.
Слайд 14Формулы правильного октаэдра
У октаэдра 8 граней, 6 вершин и 12 ребер.
Площадь одной грани октаэдра
Площадь поверхности октаэдра
Объем октаэдра
Высота октаэдра
Слайд 15В природе многие кубические кристаллы имеют форму октаэдра: алмаз, сульфат алюминия-калия, хлорид натрия, перовскит, оливин, флюорит, шпинель.
В молекулярном мире
Интересно, что шесть музыкальных нот можно расположить на вершинах октаэдра так, что каждое ребро будет представлять собой созвучную пару, а каждая грань — созвучную тройку.
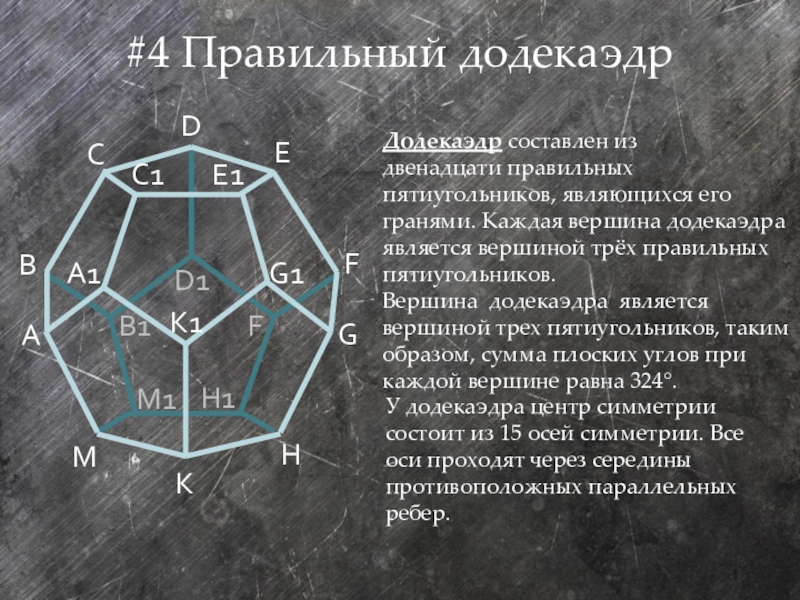
Слайд 16#4 Правильный додекаэдр
Додекаэдр составлен из двенадцати правильных пятиугольников, являющихся его гранями. Каждая вершина додекаэдра
Вершина додекаэдра является вершиной трех пятиугольников, таким образом, сумма плоских углов при каждой вершине равна 324°.
D
A
B
C
E
C1
E1
B1
F
G
H
K
M
D1
A1
M1
G1
H1
F
K1
У додекаэдра центр симметрии состоит из 15 осей симметрии. Все оси проходят через середины
противоположных параллельных ребер.
Слайд 17Формулы додекаэдра
У додекаэдра 12 граней, 20 вершин и 30 ребер.
Для
Периметр додекаэдра
Площадь одной грани додекаэдра
Площадь поверхности додекаэдра
Объем додекаэдра
Слайд 18Интересно, что форму, близкую к додекаэдру, имеет описанная Эрнстом Геккелем в 1887 году радиолярия
В 2003 году, при анализе данных космического аппарата WMAP, была выдвинута гипотеза, что Вселенная представляет собой додекаэдрическое пространство Пуанкаре (сферическое пространство Пуанкаре может быть получено из додекаэдра склеиванием каждой грани с противоположной, повёрнутой на угол Пи/5 по часовой стрелке).
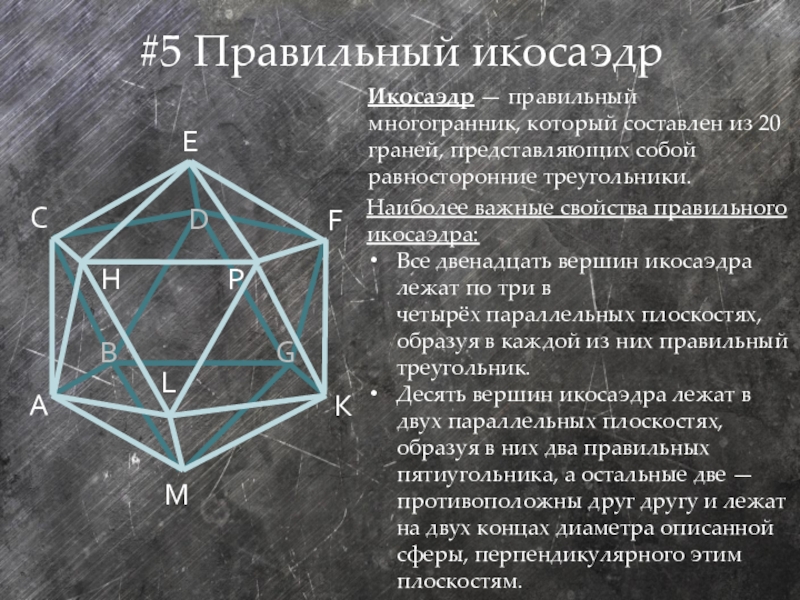
Слайд 19#5 Правильный икосаэдр
B
A
C
D
E
F
G
K
M
H
P
L
Икосаэдр — правильный многогранник, который составлен из 20 граней, представляющих собой
Наиболее важные свойства правильного икосаэдра:
Все двенадцать вершин икосаэдра лежат по три в четырёх параллельных плоскостях, образуя в каждой из них правильный треугольник.
Десять вершин икосаэдра лежат в двух параллельных плоскостях, образуя в них два правильных пятиугольника, а остальные две — противоположны друг другу и лежат на двух концах диаметра описанной сферы, перпендикулярного этим плоскостям.
Слайд 20Формулы икосаэдра
У додекаэдра 20 граней, 12 вершин и 30 ребер.
Для
Периметр икосаэдра
Площадь одной грани икосаэдра
Площадь поверхности икосаэдра
Объем икосаэдра
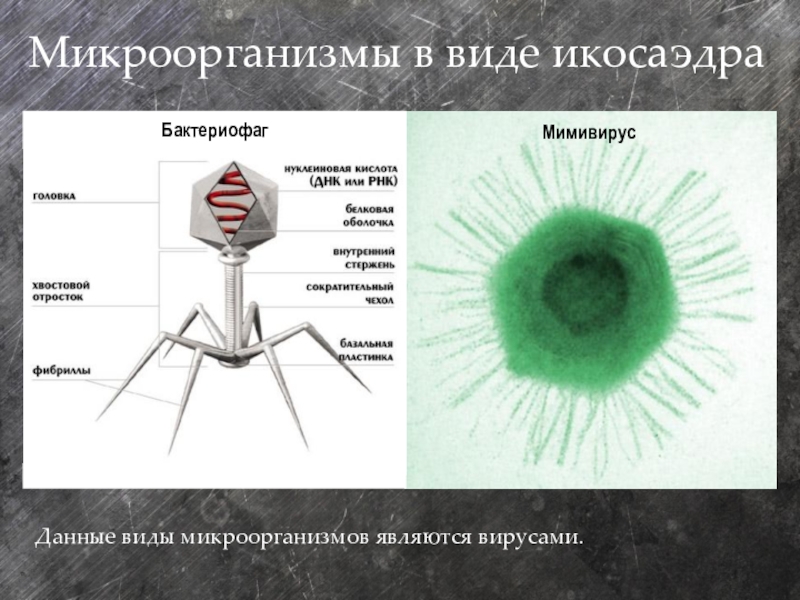
Слайд 21Микроорганизмы в виде икосаэдра
Бактериофаг
Мимивирус
Данные виды микроорганизмов являются вирусами.
Слайд 22Подведём итоги услышанного
Форма «вопрос-ответ»:
Как звали учёного, который вывел формулу, связывающую число
Какие многогранники называются правильными? Какие условия должны иметь место, чтобы многогранник назывался правильным?
Формула площади поверхности правильного тетраэдра?
Попробуйте объяснить, почему игральная кость обязательно должна иметь форму правильного многогранника?
Сколько граней у икосаэдра?
Задача.
Объём куба — 64 метра. Чему равно его ребро (в сантиметрах)?
Слайд 23Подведём итоги услышанного
Форма «вопрос-ответ»:
Как звали учёного, который вывел формулу, связывающую число
Какие многогранники называются правильными? Какие условия должны иметь место, чтобы многогранник назывался правильным?
Формула площади поверхности правильного тетраэдра?
Попробуйте объяснить, почему игральная кость обязательно должна иметь форму правильного многогранника?
Сколько граней у икосаэдра?
Задача.
Объём куба — 64 метра. Чему равно его ребро (в сантиметрах)?
ответ: Эйлер
ответ: S = a2√3
ответ: 20
ответ: 400 см