- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Правильные многогранники
Содержание
- 1. Презентация по математике на тему Правильные многогранники
- 2. Правильных многогранников вызывающе мало…
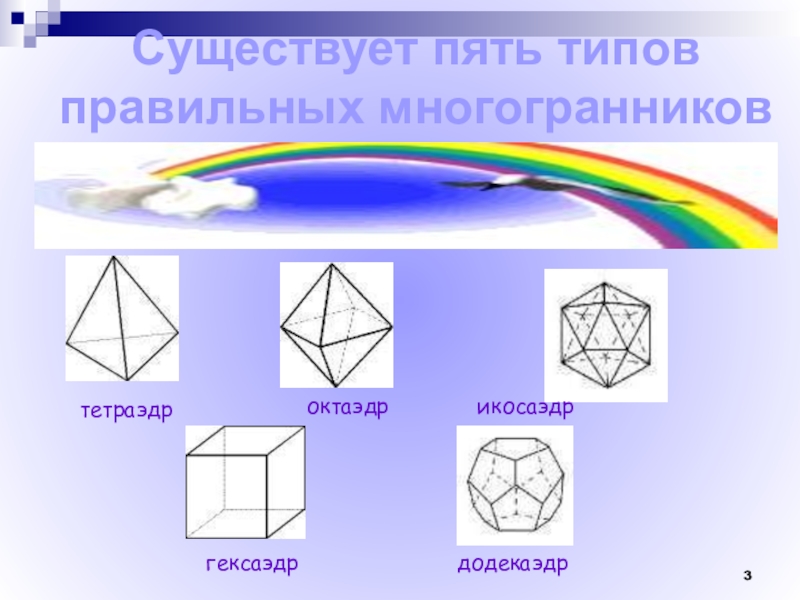
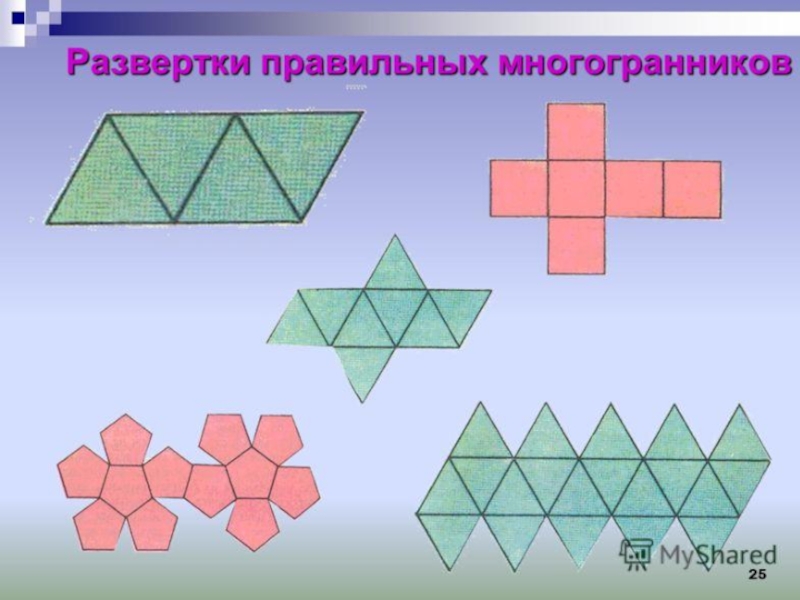
- 3. Существует пять типов правильных многогранниковтетраэдроктаэдрикосаэдргексаэдрдодекаэдр
- 4. Определение многогранника: Многогранник – это часть пространства,
- 5. ПРАВИЛЬНЫЙ МНОГОГРАННИК - выпуклый многогранник, грани которого являются
- 6. Правильный многогранник, у которого грани правильные треугольники
- 7. ОКТАЭДРПравильный многогранник, у которого грани- правильные
- 8. ИКОСОЭДРПравильный многогранник, у которого грани - правильные
- 9. КУБ -правильный многогранник, у которого грани –
- 10. ДодекаэдрПравильный многогранник, у которого грани правильные пятиугольники
- 11. Правильные многогранники называют также «платоновыми телами» -
- 12. Слайд 12
- 13. Иоганн Кеплер (1571-1630) – немецкий астроном и
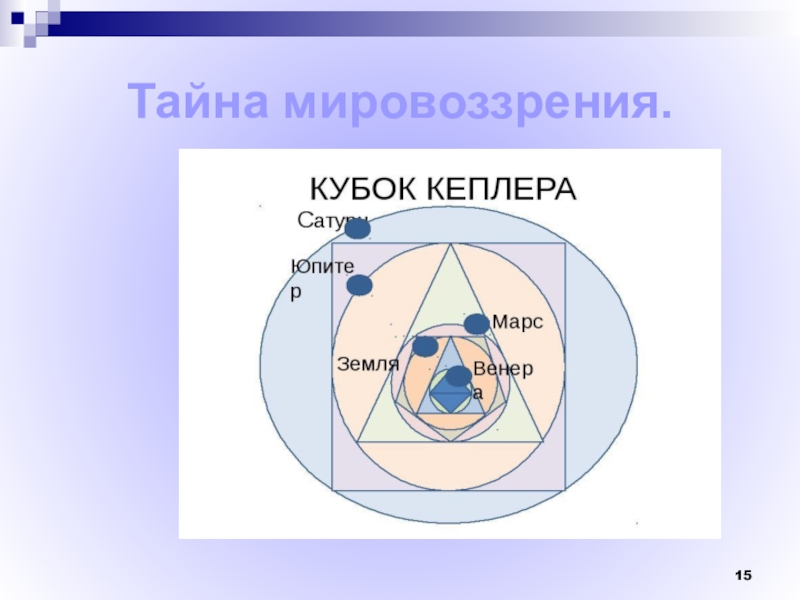
- 14. Тайна мировоззрения.
- 15. Тайна мировоззрения.
- 16. Икосаэдрово-додекаэдрова сетка на коре Земли по В. Морозову и В. Макарову
- 17. Исследовательская работа «Формула Эйлера»
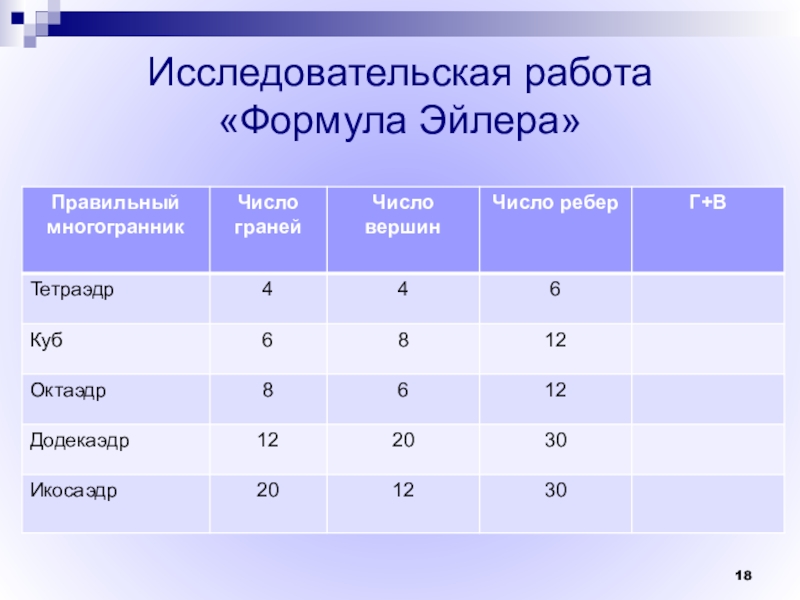
- 18. Исследовательская работа «Формула Эйлера»
- 19. Исследовательская работа «Формула Эйлера»
- 20. Теорема Эйлера. Для любого выпуклого многогранника
- 21. Слайд 21
- 22. СПАСИБО ЗА ВНИМАНИЕ
Правильных многогранников вызывающе мало…
Слайд 4Определение многогранника:
Многогранник – это часть пространства, ограниченная совокупностью конечного числа
плоских многоугольников, соединённых таким образом, что каждая сторона любого многогранника является стороной ровно одного многоугольника. Многоугольники называются гранями, их стороны – рёбрами, а вершины – вершинами.
Слайд 5ПРАВИЛЬНЫЙ МНОГОГРАННИК - выпуклый многогранник, грани которого являются правильными многоугольниками с одним
и тем же числом сторон и в каждой вершине которого сходится одно и то же число ребер.
Приведён пример правильного многогранника (икосаэдр), его гранями являются правильные (равносторонние) треугольники.
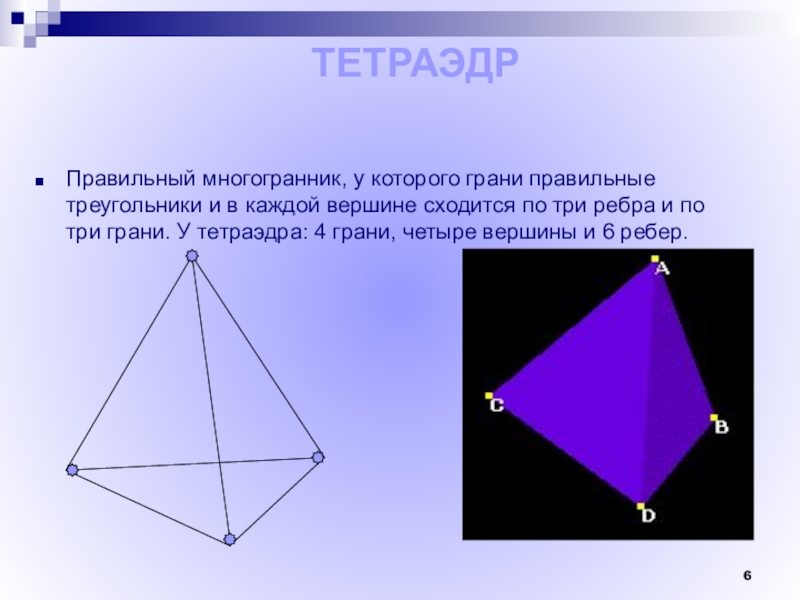
Слайд 6
Правильный многогранник, у которого грани правильные треугольники и в каждой вершине
сходится по три ребра и по три грани. У тетраэдра: 4 грани, четыре вершины и 6 ребер.
ТЕТРАЭДР
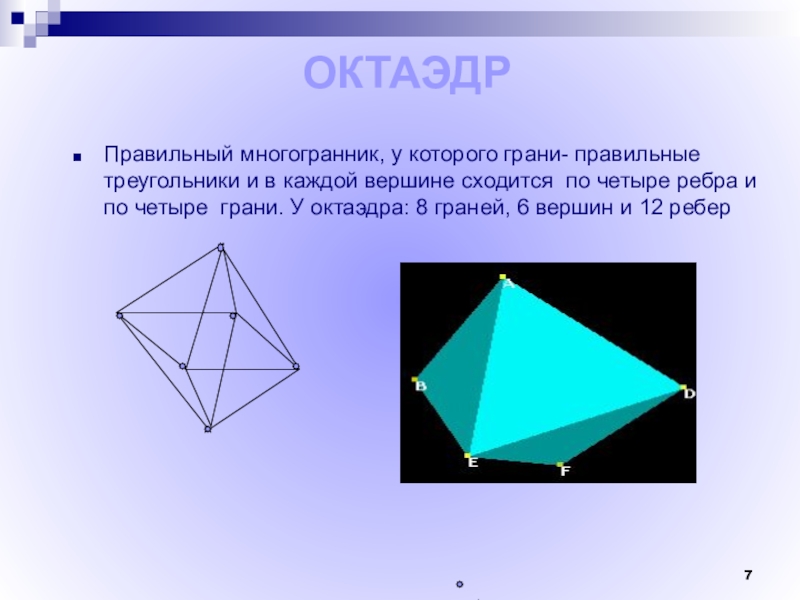
Слайд 7 ОКТАЭДР
Правильный многогранник, у которого грани- правильные треугольники и в каждой
вершине сходится по четыре ребра и по четыре грани. У октаэдра: 8 граней, 6 вершин и 12 ребер
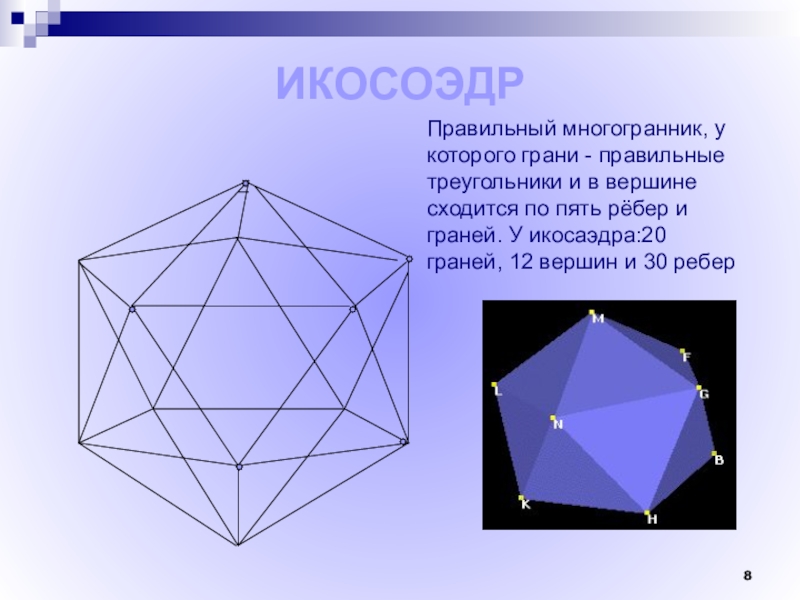
Слайд 8ИКОСОЭДР
Правильный многогранник, у которого грани - правильные треугольники и в вершине
сходится по пять рёбер и граней. У икосаэдра:20 граней, 12 вершин и 30 ребер
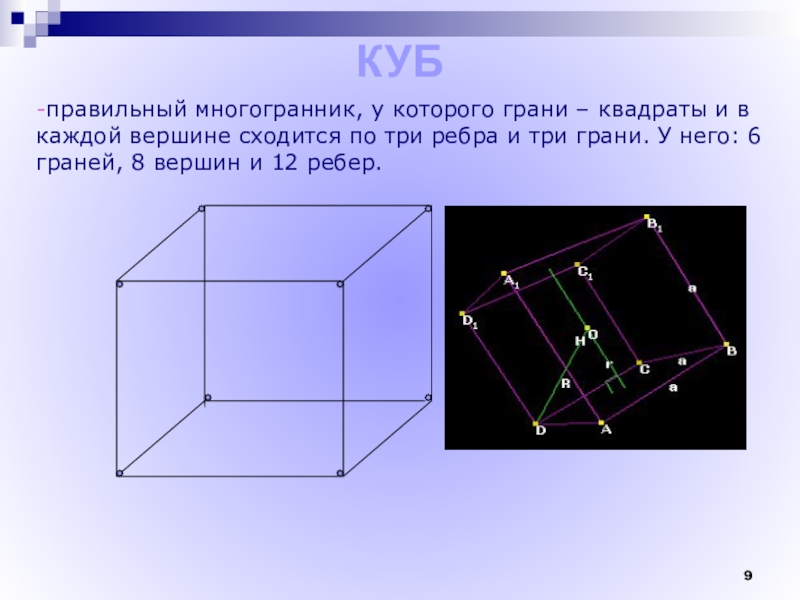
Слайд 9КУБ
-правильный многогранник, у которого грани – квадраты и в каждой
вершине сходится по три ребра и три грани. У него: 6 граней, 8 вершин и 12 ребер.
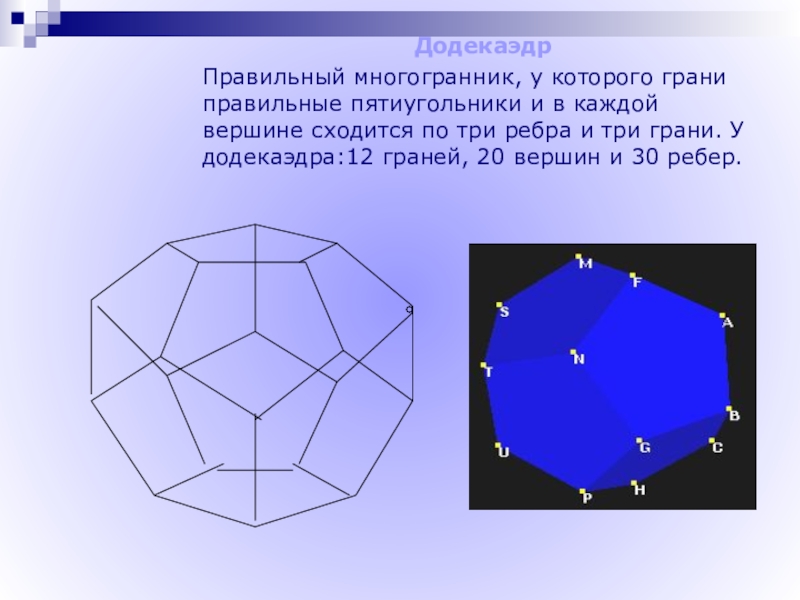
Слайд 10Додекаэдр
Правильный многогранник, у которого грани правильные пятиугольники и в каждой вершине
сходится по три ребра и три грани. У додекаэдра:12 граней, 20 вершин и 30 ребер.
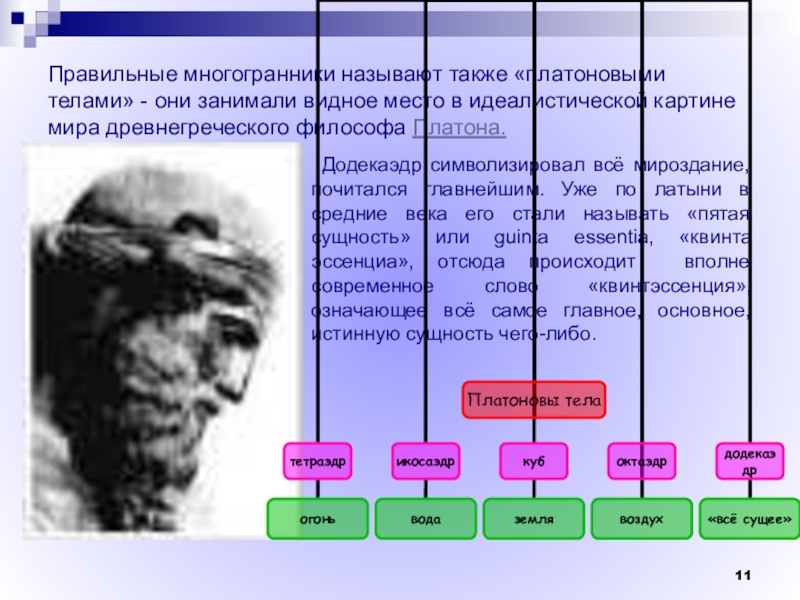
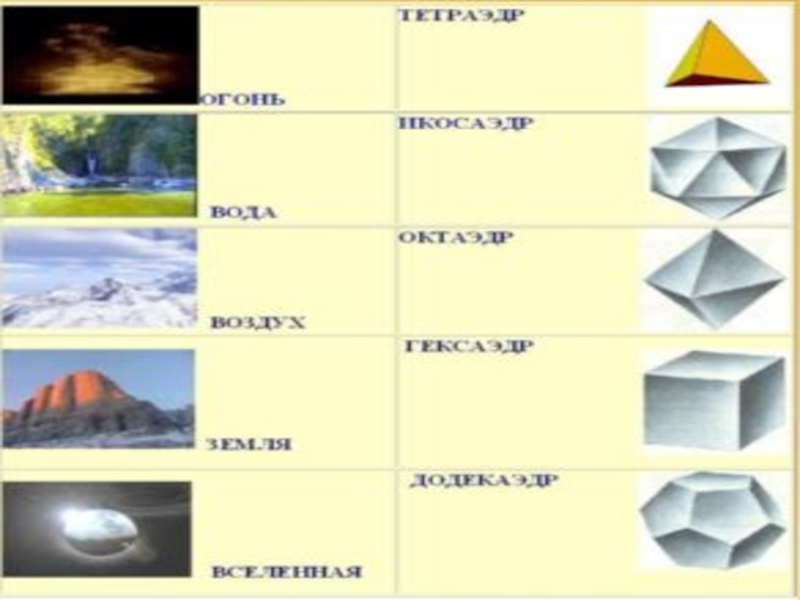
Слайд 11Правильные многогранники называют также «платоновыми телами» - они занимали видное место
в идеалистической картине мира древнегреческого философа Платона.
Додекаэдр символизировал всё мироздание, почитался главнейшим. Уже по латыни в средние века его стали называть «пятая сущность» или guinta essentia, «квинта эссенциа», отсюда происходит вполне современное слово «квинтэссенция», означающее всё самое главное, основное, истинную сущность чего-либо.
Слайд 13Иоганн Кеплер (1571-1630) – немецкий астроном и математик.
Один из создателей
современной астрономии - открыл законы движения планет (законы Кеплера)
Слайд 20
Теорема Эйлера. Для любого выпуклого многогранника
В + Г =
Р + 2
где В – число вершин,
Г – число граней,
Р – число ребер этого
многогранника.
где В – число вершин,
Г – число граней,
Р – число ребер этого
многогранника.
