- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Площади и объемы (11 класс)
Содержание
- 1. Презентация по математике на тему Площади и объемы (11 класс)
- 2. ПЛОЩАДИ И ОБЪЕМЫПлощадь сечения многогранника.Площадь поверхности многогранника.Объем многогранника.
- 3. Задача 1.Сторона основания правильной четырехугольной пирамиды SABCD
- 4. SLMNCROYBPAKTDL1M1N1α = ∠MYM1 1. BD =
- 5. ADCBOyM1L1N1KPL1N1 =2∙OL1= 2∙(OC-L1C)=2∙(OC-1/4∙OC) = 3/2∙OCL1N1 Ответ:
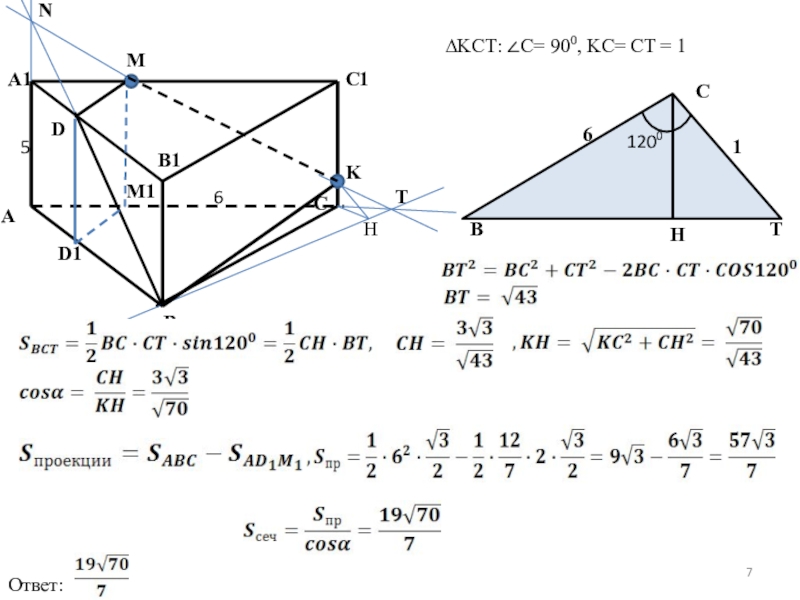
- 6. Задача 2.В правильной треугольной призме ABCA1B1C1
- 7. MKDC1BANB1CD1M156HT∆KCT: ∠С= 900, KC= CT = 1BCTH161200A1Ответ:
- 8. Задача 3.Дана правильная четырехугольная пирамида PABCD вершиной
- 9. Задача 4.В кубе ABCDA1B1C1D1 точка K –
- 10. ABCDD1NKMC1B1A1PFHELb) 1. CH ⊥PE (построение), MH⊥PE (по
- 11. ABCDNKMC1B1A1PFHELL1K1Проекция сечения LKMFP на плоскость (ABC) – есть пятиугольник CK1L1PFABCDL1PK1F331351Ответ:
- 12. Задача 5Основанием пирамиды является равнобокая трапеция с
- 13. SHCMPNBO99441. Так как H – центр вписанной
- 14. Задача 6.Основанием пирамиды является трапеция
- 15. SABDHMABCDHKL799arccos0,6∆ABK: cosA =AK:AB; 0,6 = 9:AB;
- 16. Задача 7В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что
- 17. ABCDOKC1B1D1A186b)HCH⊥BD⇒KH⊥BD (по теореме о трех перпендикулярах)∆ DCB:
- 18. Задача 8.В прямоугольном параллелепипеде ABCDA1B1C1D1 AB =
- 19. ABCDC1D1B1KPEL886Tb)Ответ: a) 40; b) 336.
- 20. Задача 9.Дан прямоугольный параллелепипед ABCDA1B1C1D1Постройте сечение параллелепипеда
- 21. Задача 10В правильной треугольной пирамиде PABC M
- 22. CPOMQFE1012b) BA∆ ABQ: ∠Q =90⁰, ∠B =60⁰,
- 23. Задача 11В правильной треугольной пирамиде PABC боковое
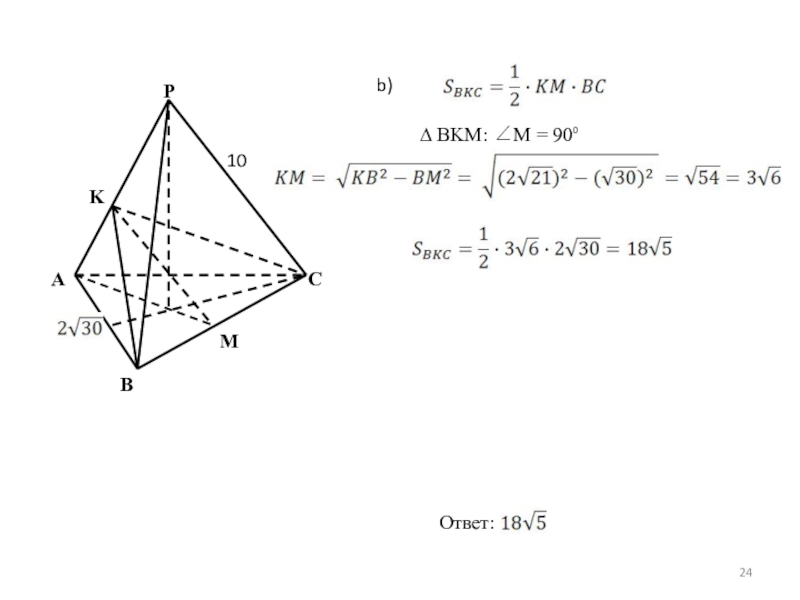
- 24. ABPKM10Cb) ∆ BKM: ∠M = 90⁰Ответ:
- 25. Задача 12.В кубе ABCDA1B1C1D1 все ребра равны
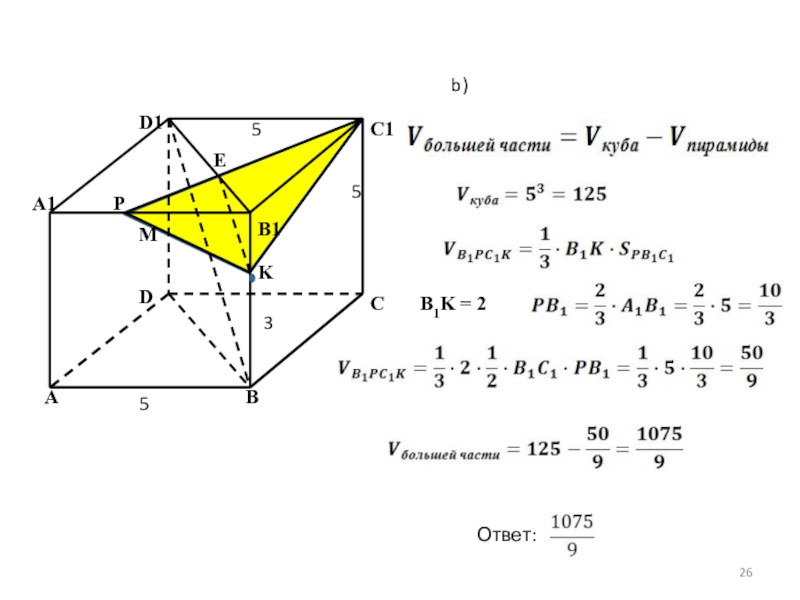
- 26. ABCDMB1C1D1KEPb) B1K = 2Ответ: A15355
- 27. Задачи для самостоятельного решения1. В правильной
- 28. Спасибо за сотрудничество!
Слайд 1Площади и объемы
Учитель: Шарова Светлана Геннадьевна,
МБОУ гимназия, г. Урюпинск, Волгоградская область
Учимся
Слайд 2ПЛОЩАДИ И ОБЪЕМЫ
Площадь сечения многогранника.
Площадь поверхности многогранника.
Объем многогранника.
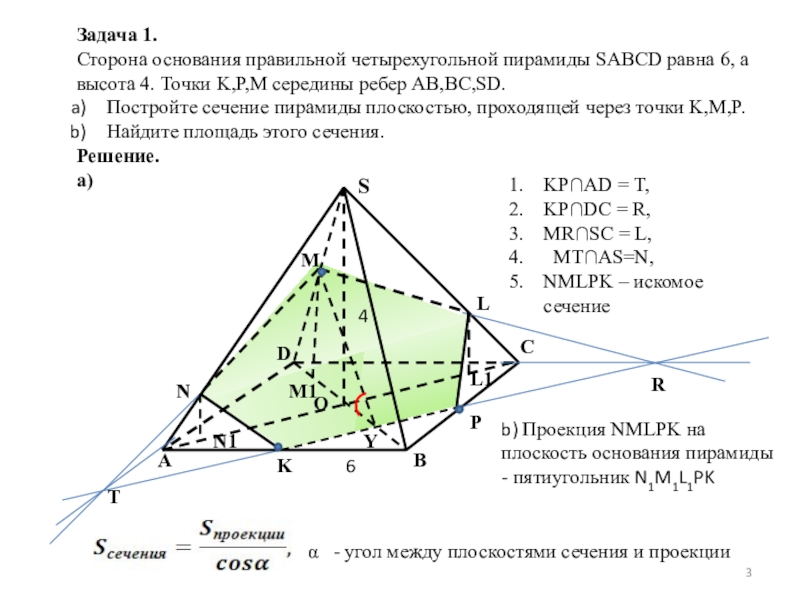
Слайд 3Задача 1.
Сторона основания правильной четырехугольной пирамиды SABCD равна 6, а высота
Постройте сечение пирамиды плоскостью, проходящей через точки K,M,P.
Найдите площадь этого сечения.
Решение.
a)
S
L
M
N
C
R
O
Y
B
P
A
K
T
D
L1
M1
N1
KP∩AD = T,
KP∩DC = R,
MR∩SC = L,
MT∩AS=N,
NMLPK – искомое сечение
b) Проекция NMLPK на плоскость основания пирамиды - пятиугольник N1M1L1PK
α - угол между плоскостями сечения и проекции
6
4
Слайд 4S
L
M
N
C
R
O
Y
B
P
A
K
T
D
L1
M1
N1
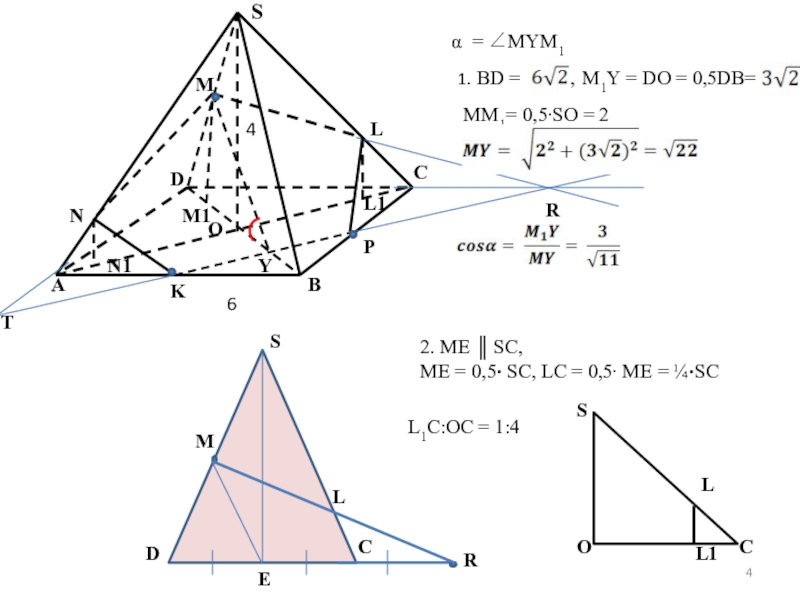
α = ∠MYM1
1. BD =
M1Y = DO = 0,5DB=
MM1= 0,5∙SO = 2
S
D
C
M
L
R
E
2. ME ║ SC,
ME = 0,5∙ SC, LC = 0,5∙ ME = ¼∙SC
S
O
C
L
L1
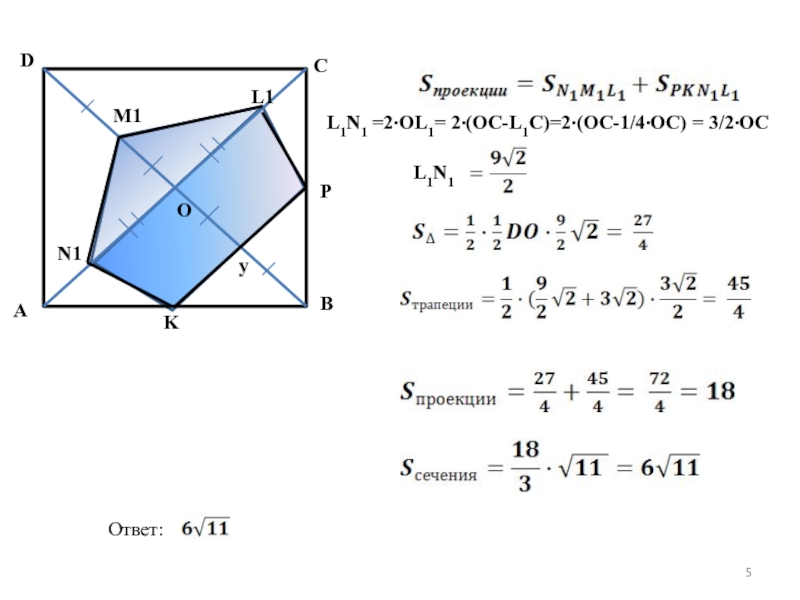
L1C:OC = 1:4
6
4
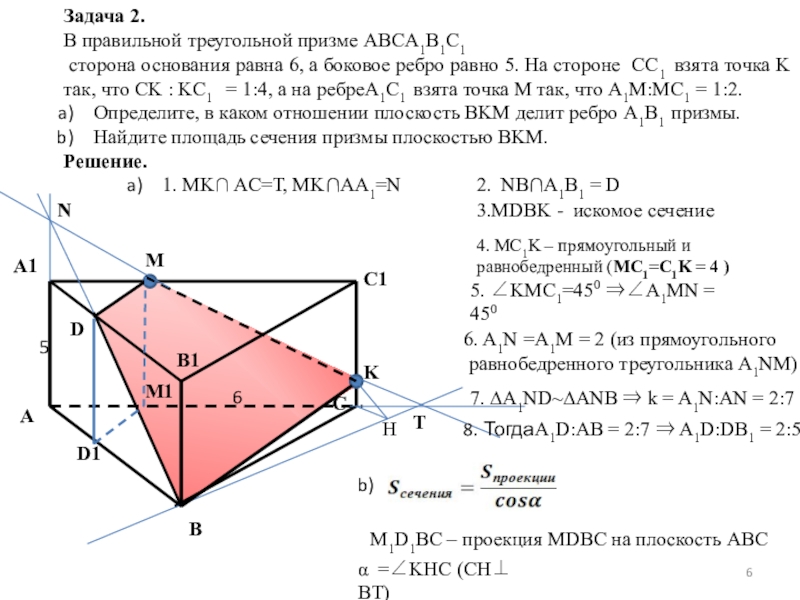
Слайд 6Задача 2.
В правильной треугольной призме ABCA1B1C1
сторона основания
Определите, в каком отношении плоскость BKM делит ребро A1B1 призмы.
Найдите площадь сечения призмы плоскостью BKM.
Решение.
A1
M
K
D
C1
B
A
N
B1
T
C
D1
M1
1. MK∩ AC=T, MK∩AA1=N
2. NB∩A1B1 = D
3.MDBK - искомое сечение
4. MC1K – прямоугольный и равнобедренный (MC1=C1K = 4 )
5. ∠KMC1=450 ⇒∠A1MN = 450
6. A1N =A1M = 2 (из прямоугольного
равнобедренного треугольника A1NM)
7. ∆A1ND~∆ANB ⇒ k = A1N:AN = 2:7
5
6
8. ТогдаA1D:AB = 2:7 ⇒ A1D:DB1 = 2:5
b)
H
M1D1BC – проекция MDBC на плоскость ABC
α =∠KHC (CH⊥ BT)
Слайд 8Задача 3.
Дана правильная четырехугольная пирамида PABCD вершиной в точке P. Через
Докажите, что плоскость α делит ребро BP в отношении 2:1, считая от точки B.
Найдите площадь сечения пирамиды плоскостью α, если известно, что PA = 10, AC = 16.
Решение.
A
D
C
B
P
M
O
E
N
Пусть M – середина AB, CM∩BD = E. Так как PO⊥(ABC) и α⊥(ABC), то α║PO. Значит, α∩ (PBD) = NE, NE║PO. Сечение NCM –искомое.
P
O
A
B
C
D
M
E
K
∆ MBE~∆KOE⇒ OE:BE=OK:MB , OK=OP-KP=½AB-½MB =½MB
Таким образом,
OE:BE = 1:2
По теореме о пропорциональных отрезках OE:BE = PN:NB.
Значит, BN:NP = 2:1.
b)
10
16
Ответ:
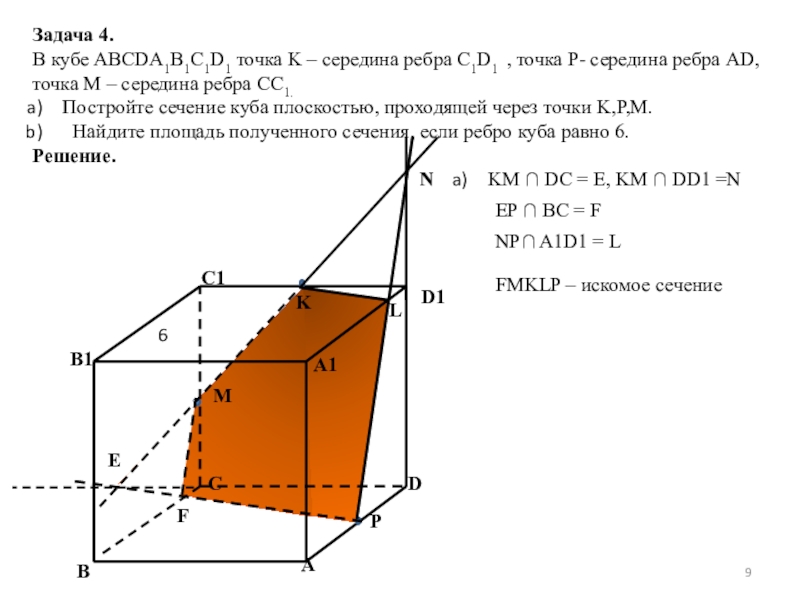
Слайд 9Задача 4.
В кубе ABCDA1B1C1D1 точка K – середина ребра C1D1 ,
Постройте сечение куба плоскостью, проходящей через точки K,P,M.
Найдите площадь полученного сечения, если ребро куба равно 6.
Решение.
A
B
C
D
D1
C1
B1
A1
M
P
K
E
N
L
F
KM ∩ DC = E, KM ∩ DD1 =N
EP ∩ BC = F
NP∩ A1D1 = L
FMKLP – искомое сечение
6
Слайд 10A
B
C
D
D1
N
K
M
C1
B1
A1
P
F
H
E
L
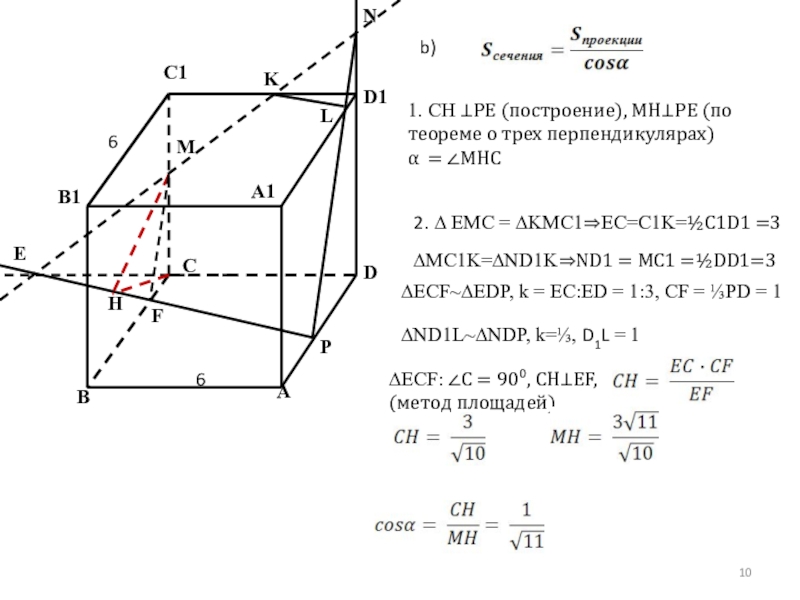
b)
1. CH ⊥PE (построение), MH⊥PE (по теореме о трех перпендикулярах)
α
2. ∆ EMC = ∆KMC1⇒EC=C1K=½C1D1 =3
∆MC1K=∆ND1K⇒ND1 = MC1 =½DD1=3
∆ECF~∆EDP, k = EC:ED = 1:3, CF = ⅓PD = 1
∆ND1L~∆NDP, k=⅓, D1L = 1
∆ECF: ∠С = 90⁰, СH⊥EF,
(метод площадей)
6
6
Слайд 11A
B
C
D
N
K
M
C1
B1
A1
P
F
H
E
L
L1
K1
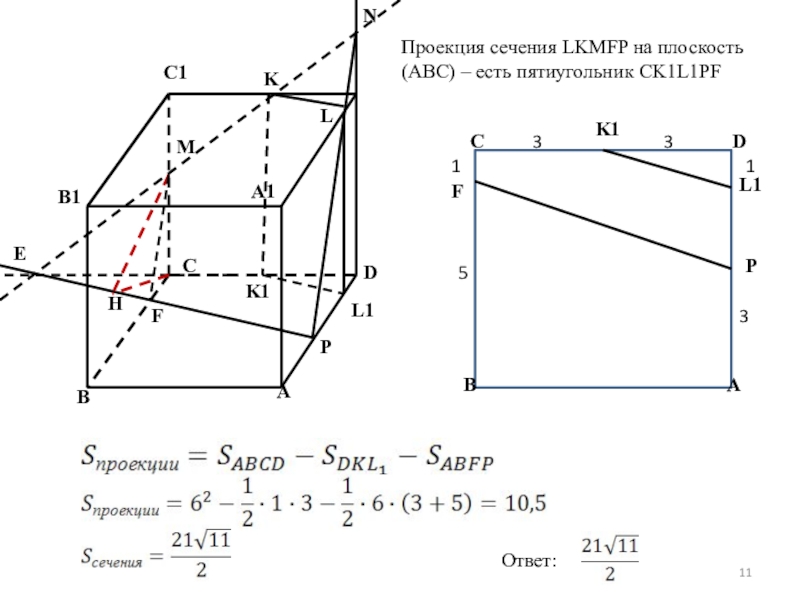
Проекция сечения LKMFP на плоскость (ABC) – есть пятиугольник CK1L1PF
A
B
C
D
L1
P
K1
F
3
3
1
3
5
1
Ответ:
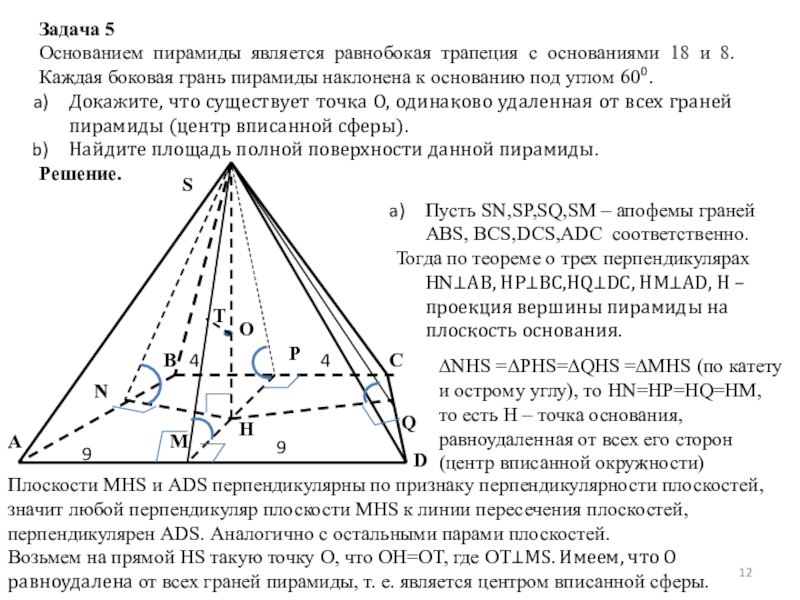
Слайд 12Задача 5
Основанием пирамиды является равнобокая трапеция с основаниями 18 и 8.
Докажите, что существует точка О, одинаково удаленная от всех граней пирамиды (центр вписанной сферы).
Найдите площадь полной поверхности данной пирамиды.
Решение.
S
H
C
D
M
Q
P
N
B
A
O
9
9
4
4
Пусть SN,SP,SQ,SM – апофемы граней ABS, BCS,DCS,ADC соответственно.
Тогда по теореме о трех перпендикулярах HN⊥AB, HP⊥BC,HQ⊥DC, HM⊥AD, H – проекция вершины пирамиды на плоскость основания.
∆NHS =∆PHS=∆QHS =∆MHS (по катету и острому углу), то HN=HP=HQ=HM,
то есть H – точка основания, равноудаленная от всех его сторон (центр вписанной окружности)
Плоскости MHS и ADS перпендикулярны по признаку перпендикулярности плоскостей, значит любой перпендикуляр плоскости MHS к линии пересечения плоскостей, перпендикулярен ADS. Аналогично с остальными парами плоскостей.
Возьмем на прямой HS такую точку O, что OH=OT, где OT⊥MS. Имеем, что О равноудалена от всех граней пирамиды, т. е. является центром вписанной сферы.
T
Слайд 13S
H
C
M
P
N
B
O
9
9
4
4
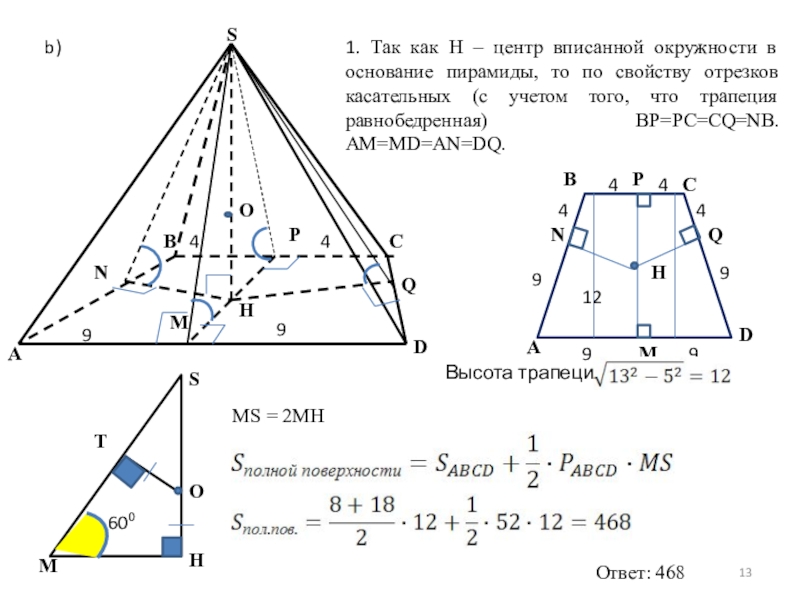
1. Так как H – центр вписанной окружности в основание пирамиды,
b)
A
D
Q
A
B
C
D
P
M
Q
N
9
9
9
9
4
4
4
4
H
12
Высота трапеции
M
H
S
60⁰
O
T
MS = 2MH
Ответ: 468
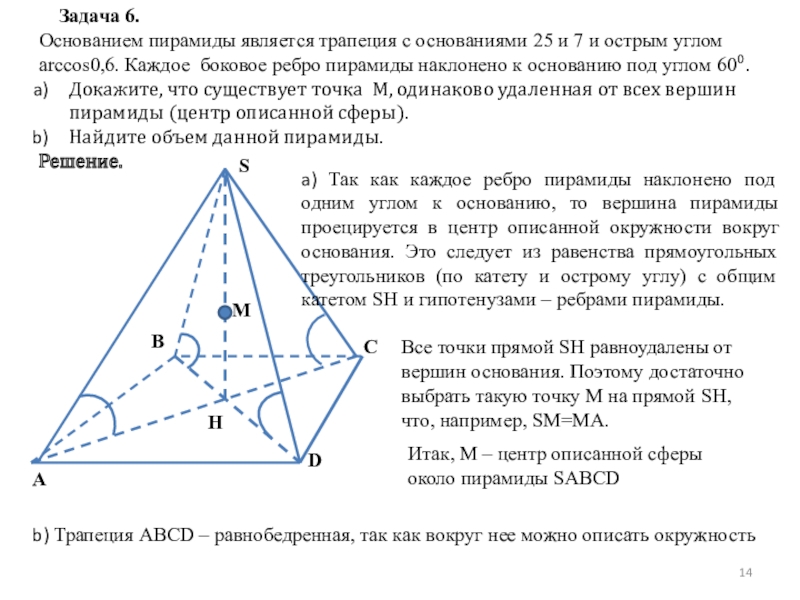
Слайд 14 Задача 6.
Основанием пирамиды является трапеция с основаниями 25 и
Докажите, что существует точка M, одинаково удаленная от всех вершин пирамиды (центр описанной сферы).
Найдите объем данной пирамиды.
Решение.
S
A
B
C
D
H
M
a) Так как каждое ребро пирамиды наклонено под одним углом к основанию, то вершина пирамиды проецируется в центр описанной окружности вокруг основания. Это следует из равенства прямоугольных треугольников (по катету и острому углу) с общим катетом SH и гипотенузами – ребрами пирамиды.
Все точки прямой SH равноудалены от вершин основания. Поэтому достаточно выбрать такую точку M на прямой SH, что, например, SM=MA.
Итак, M – центр описанной сферы около пирамиды SABCD
b) Трапеция ABCD – равнобедренная, так как вокруг нее можно описать окружность
Слайд 15S
A
B
D
H
M
A
B
C
D
H
K
L
7
9
9
arccos0,6
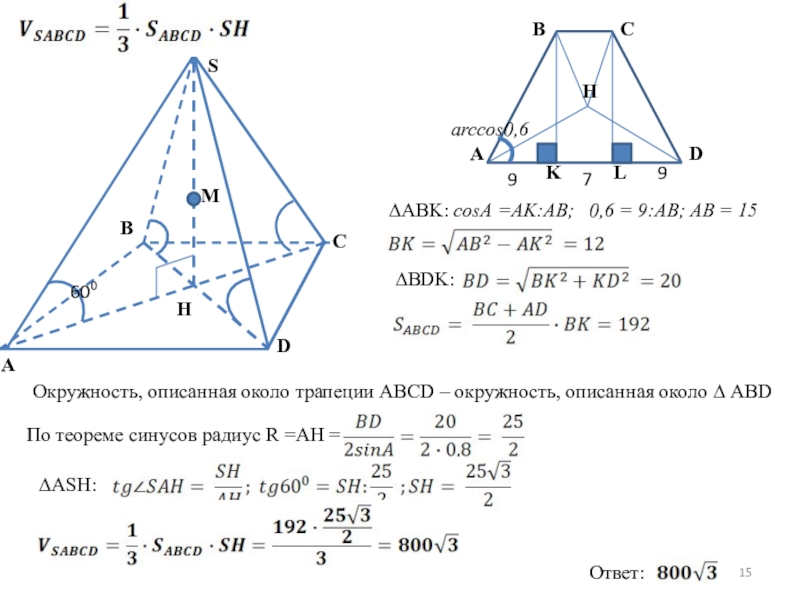
∆ABK: cosA =AK:AB; 0,6 = 9:AB; AB = 15
∆BDK:
Окружность,
По теореме синусов радиус R =AH =
∆ASH:
60⁰
Ответ:
C
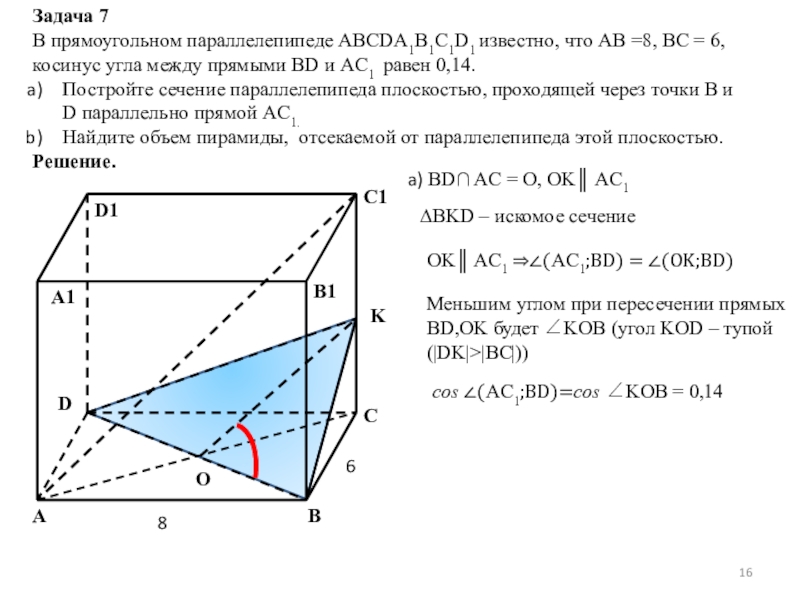
Слайд 16Задача 7
В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AB =8, BC =
Постройте сечение параллелепипеда плоскостью, проходящей через точки B и D параллельно прямой AC1.
Найдите объем пирамиды, отсекаемой от параллелепипеда этой плоскостью.
Решение.
A
B
C
D
O
K
C1
B1
D1
A1
8
6
a) BD∩ AC = O, OK║ AC1
∆BKD – искомое сечение
OK║ AC1 ⇒∠(AC1;BD) = ∠(OK;BD)
Меньшим углом при пересечении прямых BD,OK будет ∠KOB (угол KOD – тупой (|DK|>|BC|))
cos ∠(AC1;BD)=cos ∠KOB = 0,14
Слайд 17A
B
C
D
O
K
C1
B1
D1
A1
8
6
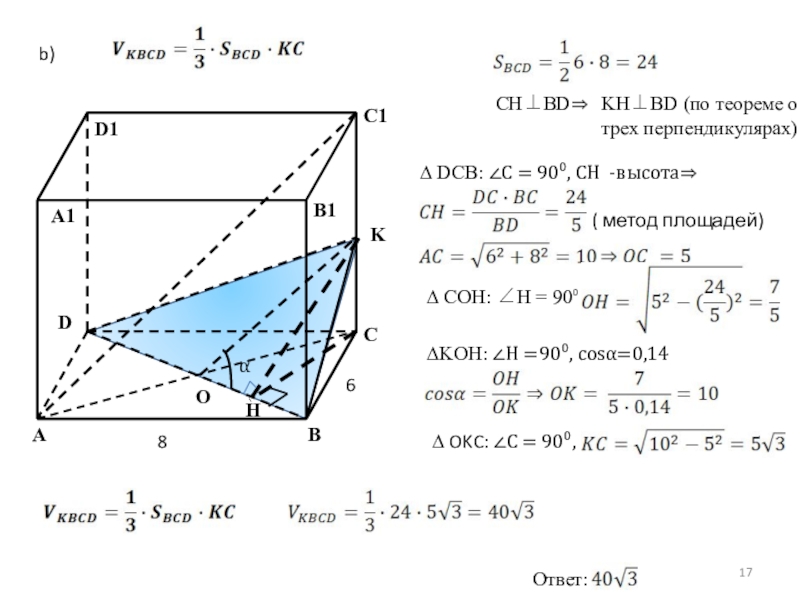
b)
H
CH⊥BD⇒
KH⊥BD (по теореме о трех перпендикулярах)
∆ DCB: ∠С = 90⁰, CH
( метод площадей)
∆ COH: ∠H = 90⁰
∆KOH: ∠H =90⁰, cosα=0,14
α
∆ OKC: ∠С = 90⁰,
Ответ:
Слайд 18Задача 8.
В прямоугольном параллелепипеде ABCDA1B1C1D1 AB = BC = 8, BB1
Площадь сечения параллелепипеда плоскостью, проходящей через точки K и P параллельно прямой BD1 ;
Объем большей части параллелепипеда, отсекаемой от него этой плоскостью.
Решение.
A
B
C
D
C1
D1
B1
A1
K
P
E
L
8
8
6
Плоскость сечения пересечет плоскость BD1B1
(в которой лежит BD1) по прямой (содержащей точку K), параллельной BD1 , так как BD1 по условию параллельна плоскости сечения.
KE║BD1 , E- середина B1D1.
PE∩A1B1 =L.
Соединяем LK
Проводим в плоскости DCC1 через точку P прямую , параллельную LK (параллельные плоскости пересекаются третьей по параллельным прямым).
T
LPTK – искомое сечение.
LPTK –прямоугольник, так как LP║ A1D1 (P – середина D1C1 по условию, E – центр A1B1C1D1 ), A1D1 ⊥ AA1B1 , то есть A1D1⊥LK.
LP = 8, PT =
Слайд 20Задача 9.
Дан прямоугольный параллелепипед ABCDA1B1C1D1
Постройте сечение параллелепипеда плоскостью, проходящей через точки
Найдите отношение объемов многогранников, на которые делит параллелепипед эта плоскость.
Решение.
A
B
C
D
L
M
B1
C1
D1
A1
a) AC∩BD = L
LM║ BD1 , M – середина DD1
∆ AMC - искомое сечение
b) Построенное сечение отсекает от прямоугольного параллелепипеда пирамиду ACDM
Ответ: 11
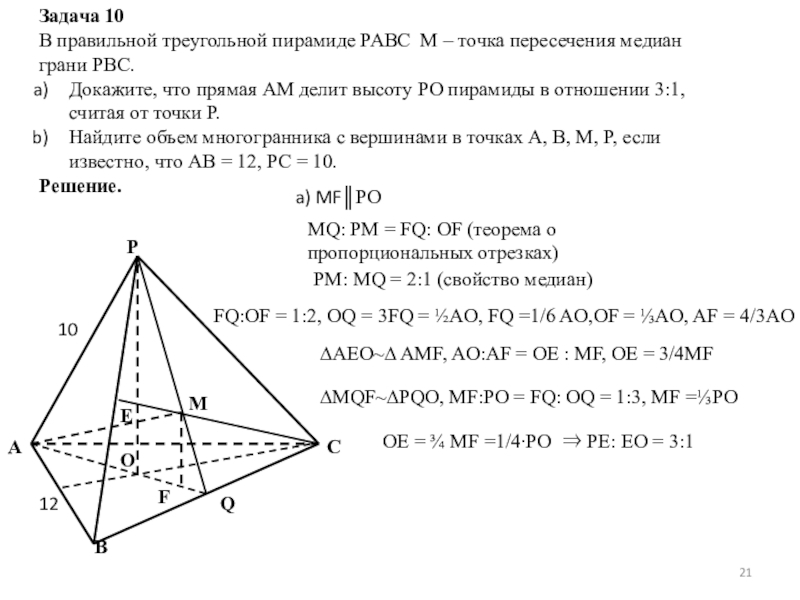
Слайд 21Задача 10
В правильной треугольной пирамиде PABC M – точка пересечения медиан
Докажите, что прямая AM делит высоту PO пирамиды в отношении 3:1, считая от точки P.
Найдите объем многогранника с вершинами в точках A, B, M, P, если известно, что AB = 12, PC = 10.
Решение.
A
B
C
P
O
M
Q
F
E
10
12
a) MF║PO
MQ: PM = FQ: OF (теорема о пропорциональных отрезках)
PM: MQ = 2:1 (свойство медиан)
FQ:OF = 1:2, OQ = 3FQ = ½AO, FQ =1/6 AO,OF = ⅓AO, AF = 4/3AO
∆AEO~∆ AMF, AO:AF = OE : MF, OE = 3/4MF
∆MQF~∆PQO, MF:PO = FQ: OQ = 1:3, MF =⅓PO
OE = ¾ MF =1/4∙PO ⇒ PE: EO = 3:1
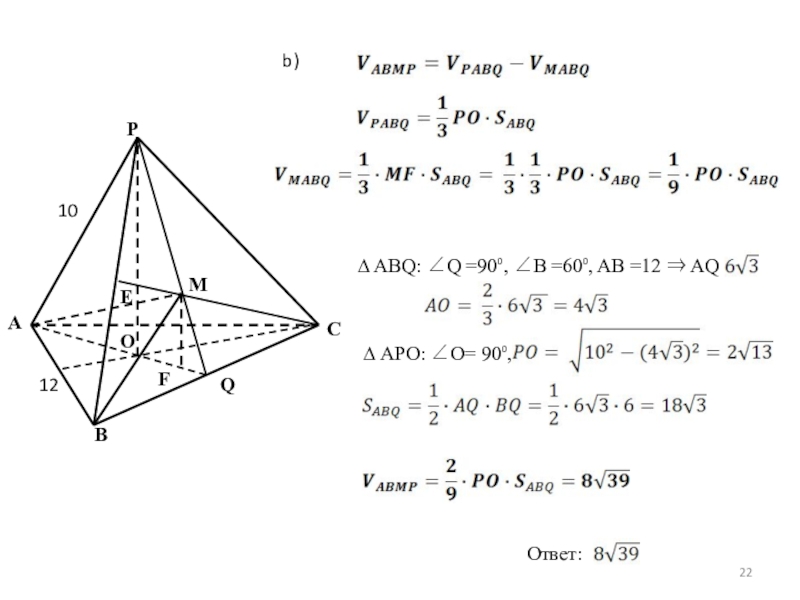
Слайд 23Задача 11
В правильной треугольной пирамиде PABC боковое ребро равно 10, а
Докажите, что плоскость α делит пирамиду PABC на два многогранника, объемы которых относятся как 2:3.
Найдите площадь сечения пирамиды PABC плоскостью α.
Решение.
A
B
C
P
K
M
a) BC α, α⊥AP, α∩AP = K, PK⊥α, AK⊥α
A
P
B
K
H
10
Слайд 25Задача 12.
В кубе ABCDA1B1C1D1 все ребра равны 5. На его ребре
Докажите, что A1P:PB1 = 1: 2, где P – точка пересечения плоскости α с ребром A1B1
Найдите объем большей из двух частей куба, на которые он делится плоскостью α .
Решение.
A
B
C
D
M
B1
C1
D1
A1
K
E
P
a) В плоскости DD1B1 через точку K проведём прямую EK ║ BD1 , E € D1B1
В плоскости A1D1C1 : C1E∩A1B1 = P
Плоскость PC1K ║ BD1 по признаку параллельности прямой и плоскости
∆EB1K~∆D1B1B ⇒ EB1: D1B1 = B1K: B1B = 2: 5
Значит, EB1: D1E= = 2: 3
∆PEB1~∆C1ED1 ⇒ PB1:C1D1=EB1 : D1E = 2: 3
C1D1 = A1B1, значит, PB1:C1D1 = PB1:A1B1 = 2:3
Таким образом, A1P: PB1 = 1:2
5
3
5
5
Слайд 27 Задачи для самостоятельного решения
1. В правильной треугольной пирамиде SABC сторона основания AB равна 12,
Докажите, что плоскость α делит медиану CE основания отношении 5:1, считая от точки C.
Найдите объём пирамиды, вершиной которой является точка C, а основанием - сечение пирамиды SABC плоскостью α.
2. В кубе ABCDA1B1C1D1 все рёбра равны 6. На его ребре BB1 отмечена точка K так, что KB=5. Через точки K и C1 проведена плоскость α параллельная прямой BD1.
а) Докажите, что A1P:PB1=4:1, где P — точка пересечения плоскости α с ребром A1B1.
б) Найдите объём большей из двух частей куба, на которые он делится плоскостью α.
3. В правильной треугольной пирамиде SABC сторона основания AB равна 6, а боковое ребро SA равно 4. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите периметр многоугольника, являющегося сечением пирамиды SABC плоскостью α