- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Площадь треугольника
Содержание
- 1. Презентация по математике на тему Площадь треугольника
- 2. Площадь треугольника!!!Площадь треугольника равна половине произведения двух
- 3. Слайд 3
- 4. Запомни!
- 5. Задача № 1. Стороны треугольника 8см и
- 6. Вопрос для обсуждения: При каком значении угла
- 7. Задача № 2. Найдите площадь правильного треугольника
- 8. Запомни! Площадь правильного треугольника.
- 9. Задача № 3. Площадь параллелограмма равна половине
- 10. Слайд 10
- 11. Запомни! - площадь параллелограммаПлощадь параллелограмма d1 и
- 12. Вопрос для обсуждения: Могут ли два параллелограмма
- 13. Герон Александрийский
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Вывод формулы Герона ,
- 20. 3) Из основного тригонометрического тождества sin2C+cos2C=1,
- 21. Таким образом S =
- 22. Запомни!Формула Герона для вычисления площади треугольника
- 23. Задача № 4. Площадь треугольника, описанного около
- 24. Задача № 5. Докажите, что
- 25. Запомни!
- 26. Задача для всех: Стороны треугольника
Площадь треугольника!!!Площадь треугольника равна половине произведения двух сторон на синус угла между ними.
Слайд 2Площадь треугольника!!!
Площадь треугольника равна половине
произведения двух сторон на синус угла
между ними.
S =
S =
Слайд 3
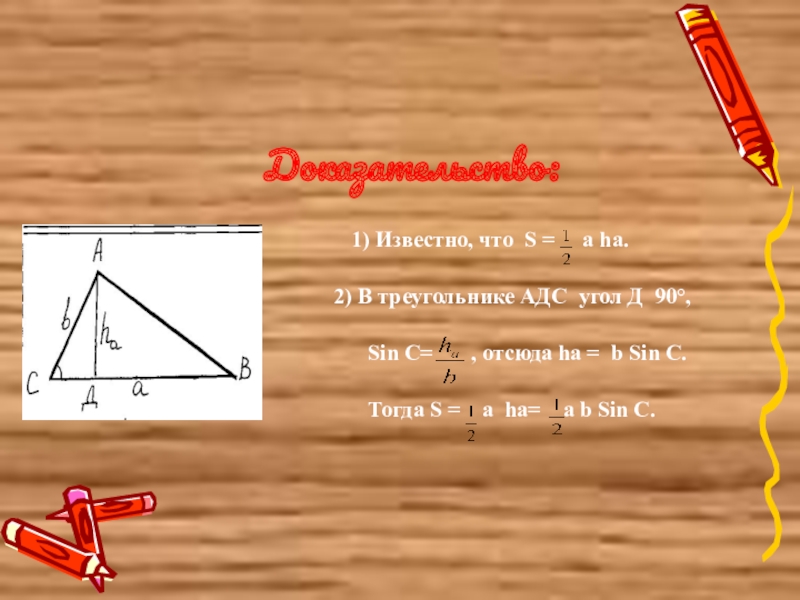
Доказательство:
1) Известно, что S = а hа.
2) В треугольнике АДС угол Д 90°,
Sin C= , отсюда hа = b Sin C.
Тогда S = а hа= а b Sin C.
1) Известно, что S = а hа.
2) В треугольнике АДС угол Д 90°,
Sin C= , отсюда hа = b Sin C.
Тогда S = а hа= а b Sin C.
Слайд 5Задача № 1. Стороны треугольника 8см и 5см, а угол между
ними 30°.Найдите площадь треугольника.
Дано : Решение:
АВС
АВ = 5 см S = = *8*5 sin30°= 20*=10 (см²).
АС = 8 см.
= 30 °.
S - ?
Ответ : площадь треугольника АВС равна 10 см²
Дано : Решение:
АВС
АВ = 5 см S = = *8*5 sin30°= 20*=10 (см²).
АС = 8 см.
= 30 °.
S - ?
Ответ : площадь треугольника АВС равна 10 см²
Слайд 6Вопрос для обсуждения:
При каком значении угла С площадь треугольника будет
наибольшая?
( Площадь треугольника наибольшая, если угол С= 90°, т.к. наибольшее значение sin=1 при =90°, а для остальных углов от 0° до 180° меньше 1.)
( Площадь треугольника наибольшая, если угол С= 90°, т.к. наибольшее значение sin=1 при =90°, а для остальных углов от 0° до 180° меньше 1.)
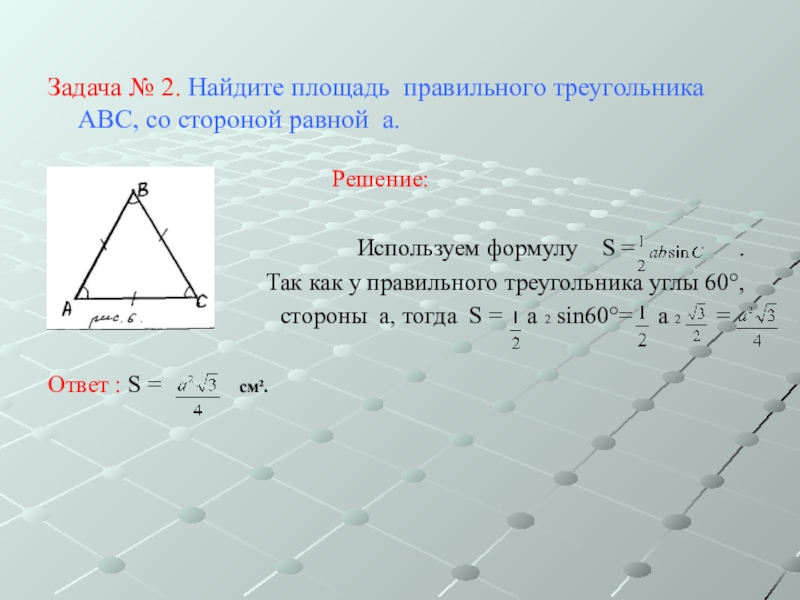
Слайд 7Задача № 2. Найдите площадь правильного треугольника АВС, со стороной равной
а.
Решение:
Используем формулу S = .
Так как у правильного треугольника углы 60°,
стороны а, тогда S = а 2 sin60°= а 2 =
Ответ : S = см².
Решение:
Используем формулу S = .
Так как у правильного треугольника углы 60°,
стороны а, тогда S = а 2 sin60°= а 2 =
Ответ : S = см².
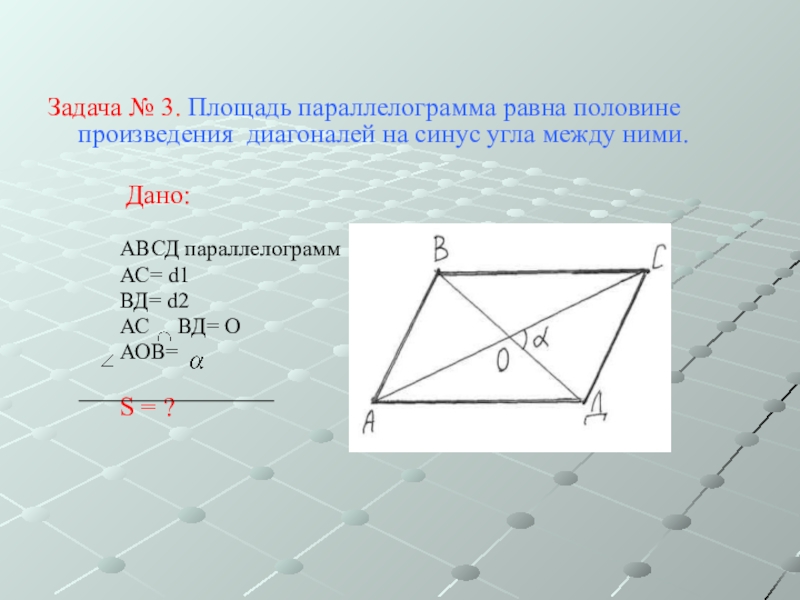
Слайд 9Задача № 3. Площадь параллелограмма равна половине произведения диагоналей на синус
угла между ними.
Дано:
АВСД параллелограмм
АС= d1
ВД= d2
АС ВД= О
АОВ=
S = ?
Дано:
АВСД параллелограмм
АС= d1
ВД= d2
АС ВД= О
АОВ=
S = ?
Слайд 10
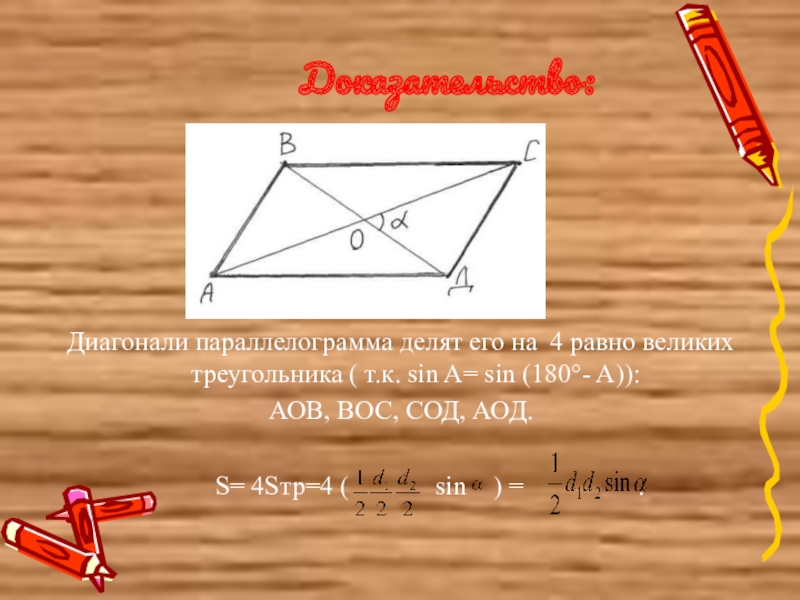
Доказательство:
Диагонали параллелограмма делят его на 4 равно великих треугольника ( т.к. sin A= sin (180°- A)):
АОВ, ВОС, СОД, АОД.
S= 4Sтр=4 ( sin ) = .
Диагонали параллелограмма делят его на 4 равно великих треугольника ( т.к. sin A= sin (180°- A)):
АОВ, ВОС, СОД, АОД.
S= 4Sтр=4 ( sin ) = .
Слайд 11Запомни!
- площадь параллелограмма
Площадь параллелограмма d1 и d2 –
диагонали параллелограмма- угол между диагоналями.
Частные случаи:
Если d1=d2 ( например прямоугольник) , то получим
Если угол между диагоналями 90°(например, ромб, квадрат),то
Частные случаи:
Если d1=d2 ( например прямоугольник) , то получим
Если угол между диагоналями 90°(например, ромб, квадрат),то
Слайд 12Вопрос для обсуждения:
Могут ли два параллелограмма с равными диагоналями иметь
разные площади?
( Могут т.к. площадь зависит не только от диагоналей, но и от угла между ними, если углы разные, то и площади разные).
( Могут т.к. площадь зависит не только от диагоналей, но и от угла между ними, если углы разные, то и площади разные).
Слайд 19Вывод формулы Герона ,
где p- полупериметр и
а,b,c- стороны треугольника.
Решение:
1) Известно, что S = .
2)По теореме косинусов
с² = а²+ b² -2ab cosC,
отсюда
Решение:
1) Известно, что S = .
2)По теореме косинусов
с² = а²+ b² -2ab cosC,
отсюда
Слайд 20
3) Из основного тригонометрического тождества sin2C+cos2C=1,
имеем sin²C= 1 -
cos²C= ( 1- cosC )( 1 +cosC)=( 1 - )(1+ )
=
= .
Замечая, что a+b+c=2p, a+c-b=2p-2b=2(p-b), b+c-a=2p-2a=2(p-a),
a+b-c=2p-2c=2(p-c), получаем sinC= .
=
= .
Замечая, что a+b+c=2p, a+c-b=2p-2b=2(p-b), b+c-a=2p-2a=2(p-a),
a+b-c=2p-2c=2(p-c), получаем sinC= .
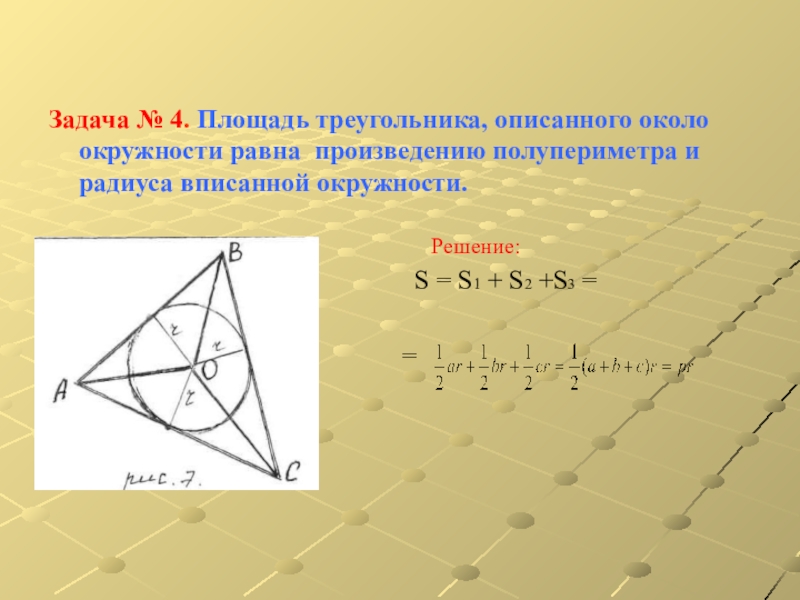
Слайд 23Задача № 4. Площадь треугольника, описанного около окружности равна
произведению полупериметра и радиуса вписанной окружности.
Решение:
S = S1 + S2 +S3 =
=
Решение:
S = S1 + S2 +S3 =
=
Слайд 24
Задача № 5. Докажите, что
, где a,b,c стороны треугольника и R радиус, описанной около треугольника окружности.
Доказательство:
1) Известно, что ,
отсюда
2) Умножая числитель и знаменатель дроби
на bc получим:
R= =
3) S=
Доказательство:
1) Известно, что ,
отсюда
2) Умножая числитель и знаменатель дроби
на bc получим:
R= =
3) S=
Слайд 25Запомни!
S=
pr, отсюда r =
S= , отсюда R= .
a,b,c- стороны треугольникаr- радиус вписанной окружности R- радиус описанной окружности
S= , отсюда R= .
a,b,c- стороны треугольникаr- радиус вписанной окружности R- радиус описанной окружности
Слайд 26Задача для всех:
Стороны треугольника
13см,
14см и 15см.
Найдите площадь треугольника и радиусы вписанной и описанной
окружностей.
Найдите площадь треугольника и радиусы вписанной и описанной
окружностей.