Площадь поверхности пирамиды.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Пирамида. Боковая поверхность пирамиды
Содержание
- 1. Презентация по математике на тему Пирамида. Боковая поверхность пирамиды
- 2. Слайд 2
- 3. Слайд 3
- 4. Слайд 4
- 5. На окраине Каира - столицы современного Египта
- 6. Пирамида Солнца (Центральная Америка к северу от Мехико город Теотиукан)
- 7. Пирамиды Гуимар (остров Тенериф)
- 8. Стеклянная пирамида в Париже (Новый вход в Лувр, высота 21,65метра)
- 9. Франкфурт: загородный дом 1896 года. Одна
- 10. Определение. Многогранник, одна грань которого произвольный многоугольник,
- 11. Построение пирамидыSПостроить плоский многоугольник.2) Отметить вершину пирамиды.3)
- 12. Определение. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на основание.
- 13. Слайд 13
- 14. Определение. Пирамида называется правильной, если в ее
- 15. Построение правильной пирамиды1. Построить основание пирамиды.2. Найти
- 16. Свойства правильной пирамиды2 свойство. Все боковые грани
- 17. Определение. Апофемой боковой грани правильной пирамиды называется
- 18. Определение. Сечение пирамиды плоскостью, проходящей через два
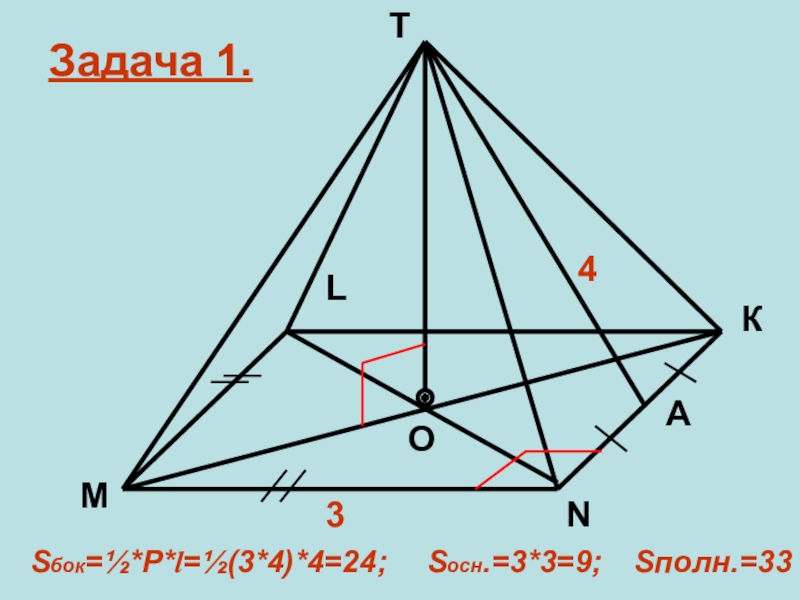
- 19. 34АМNКОLTЗадача 1.Sбок=½*Р*l=½(3*4)*4=24; Sосн.=3*3=9;Sполн.=33
- 20. Домашнее задание выучить теорию по конспекту и
- 21. Определение. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на основание.
На окраине Каира - столицы современного Египта самая высокая пирамида - пирамида Хеопса (первая половина III тысячелетия до н. э.)
Слайд 5На окраине Каира - столицы современного Египта самая высокая пирамида
- пирамида Хеопса (первая половина III тысячелетия до н. э.)
Слайд 9
Франкфурт: загородный дом 1896 года.
Одна из башен имеет форму пирамиды
и придает зданию величавый вид.
Слайд 10
Определение.
Многогранник, одна грань которого произвольный многоугольник, а остальные грани –
треугольники, имеющие общую вершину,
называется пирамидой.
называется пирамидой.
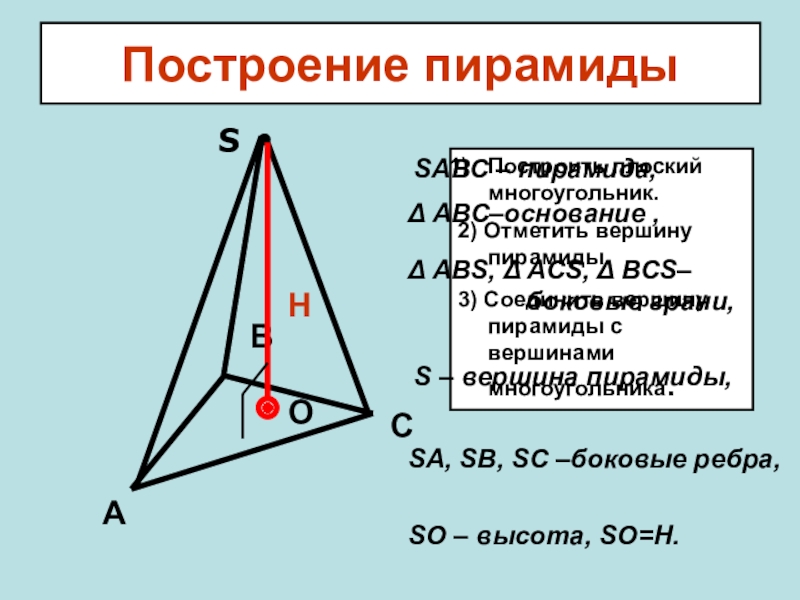
Слайд 11Построение пирамиды
S
Построить плоский многоугольник.
2) Отметить вершину пирамиды.
3) Соединить вершину пирамиды с
вершинами многоугольника.
SО – высота, SО=Н.
SА, SВ, SС –боковые ребра,
S – вершина пирамиды,
Δ АВС–основание ,
SАВС – пирамида,
О
Н
Δ АВS, Δ АСS, Δ ВСS–
боковые грани,
Слайд 12
Определение.
Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на основание.
Слайд 14
Определение.
Пирамида называется правильной, если в ее основании лежит правильный многоугольник,
а высота проходит через центр основания.
Слайд 15Построение правильной пирамиды
1. Построить основание пирамиды.
2. Найти центр основания.
3. Восставить перпендикуляр
из центра.
4. Отметить вершину пирамиды – точку, которая лежит на перпендикуляре.
5. Соединить вершину пирамиды с вершинами основания.
4. Отметить вершину пирамиды – точку, которая лежит на перпендикуляре.
5. Соединить вершину пирамиды с вершинами основания.
Слайд 16Свойства правильной пирамиды
2 свойство.
Все боковые грани правильной пирамиды – равные,
равнобедренные треугольники.
1 свойство.
Боковые ребра правильной пирамиды равны.
Слайд 17
Определение. Апофемой боковой грани правильной пирамиды называется высота этой грани, проведенная
из вершины пирамиды.
Определение. Боковой поверхностью пирамиды называется сумма площадей ее
боковых граней.
Теорема. Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему.
Sполн.= Sбок.+ Sосн.
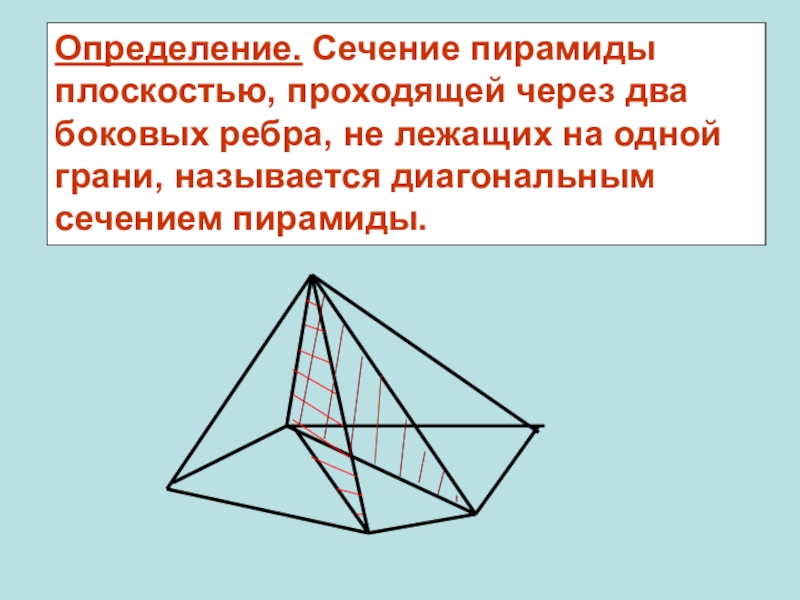
Слайд 18
Определение. Сечение пирамиды плоскостью, проходящей через два боковых ребра, не лежащих
на одной грани, называется диагональным сечением пирамиды.
Слайд 20
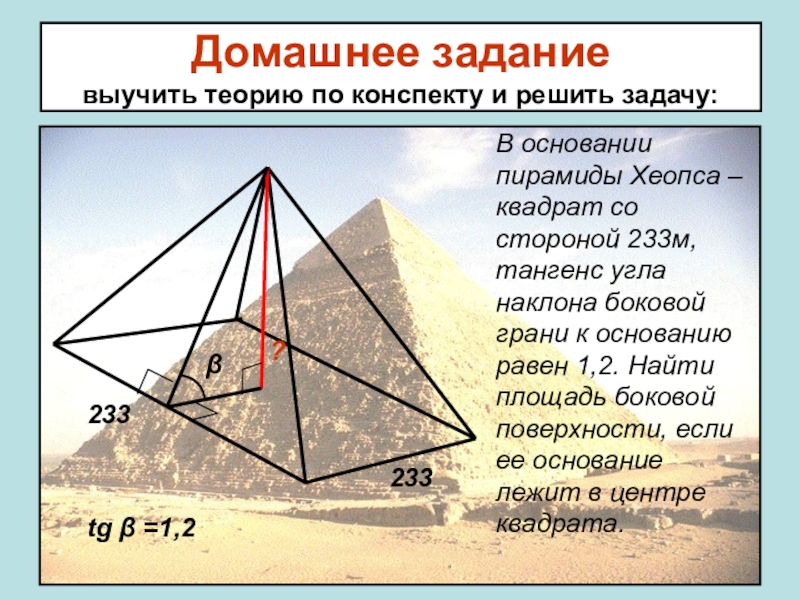
Домашнее задание
выучить теорию по конспекту и решить задачу:
В основании пирамиды Хеопса
– квадрат со стороной 233м, тангенс угла наклона боковой грани к основанию равен 1,2. Найти площадь боковой поверхности, если ее основание лежит в центре квадрата.
β
tg β =1,2
?
233
233
Слайд 21
Определение.
Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на основание.
