кызы
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Параллелепипед
Содержание
- 1. Презентация по математике на тему Параллелепипед
- 2. Развитие геометрии.Начало геометрии было положено в древности
- 3. В XVII в. Декарт благодаря методу координат
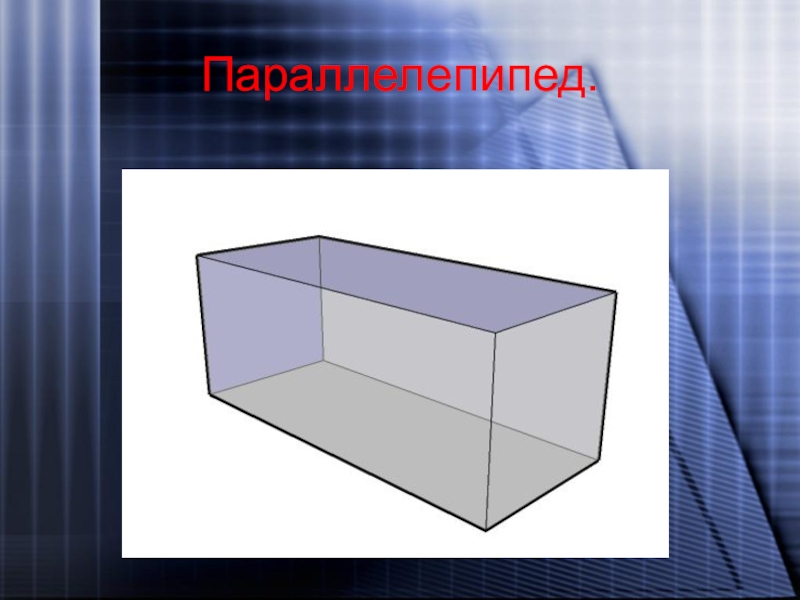
- 4. Параллелепипед.
- 5. Параллелепи́пед - (от греч. παράλλος — параллельный
- 6. Основные элементы параллелепипеда:1.Две грани параллелепипеда, не имеющие
- 7. У параллелепипедов и только у них любую
- 8. Свойства параллелепипеда:1.Противоположные грани параллелепипеда равны и параллельны.2.Все
- 9. Теорема: У параллелепипеда противолежащие грани параллельны и
- 10. Теорема: Параллелепипед симметричен относительно середины его диагонали.Важные
- 11. Произвольный параллелепипед.Объём и соотношения в наклонном параллелепипеде
- 12. Объем параллелепипеда:
- 13. В параллелепипед можно вписать тетраэдр. Объем такого тетраэдра равен 1/3 части объема параллелепипеда.
- 14. Вот так параллелепипед выглядит в развертке.
- 15. Различается несколько типов параллелепипедов:1.Прямоугольный параллелепипед. 2.Прямой параллелепипед. 3.Наклонный параллелепипед.4.Куб.
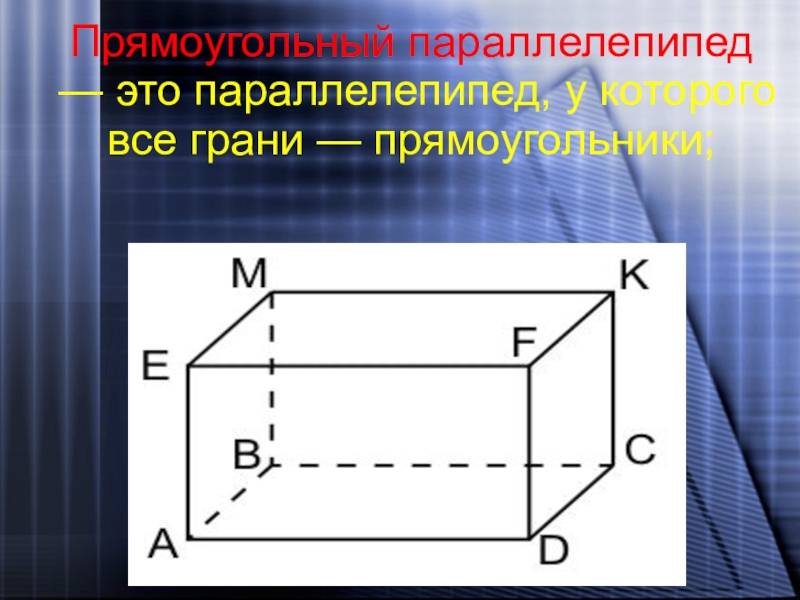
- 16. Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники;
- 17. Вывод формулы объёма прямоугольного параллелепипеда, измерения
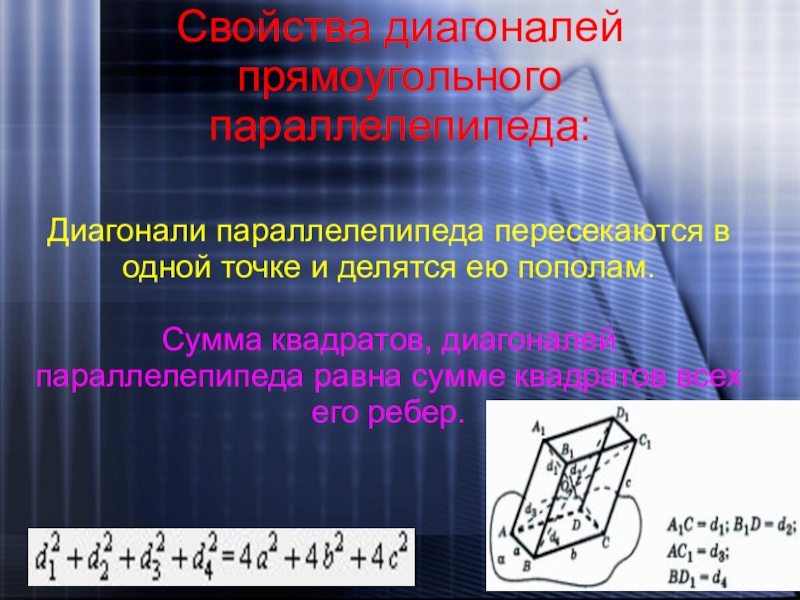
- 18. Свойства диагоналей прямоугольного параллелепипеда:Диагонали параллелепипеда пересекаются в
- 19. Площадь поверхности прямоугольного параллелепипеда равна удвоенной сумме площадей трех граней этого параллелепипеда:S= 2(Sa+Sb+Sc)= 2(ab+ bc+ ac)
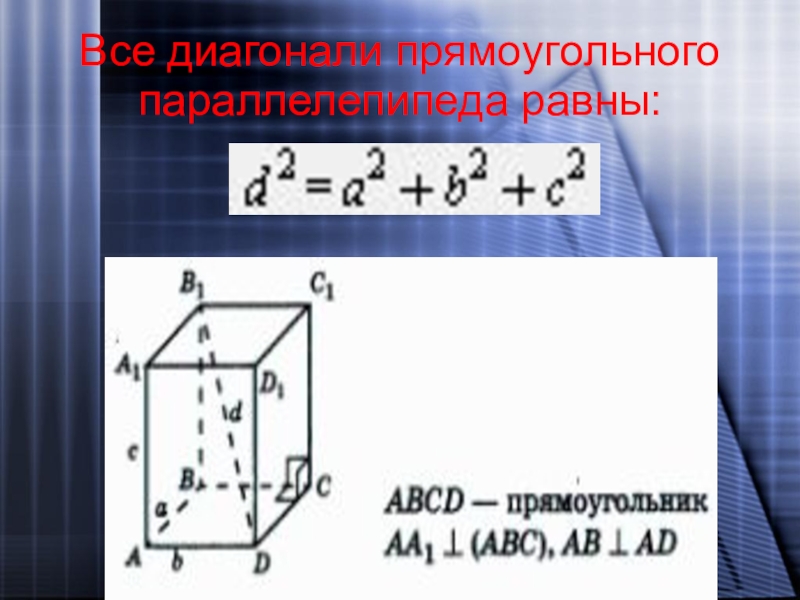
- 20. Все диагонали прямоугольного параллелепипеда равны:
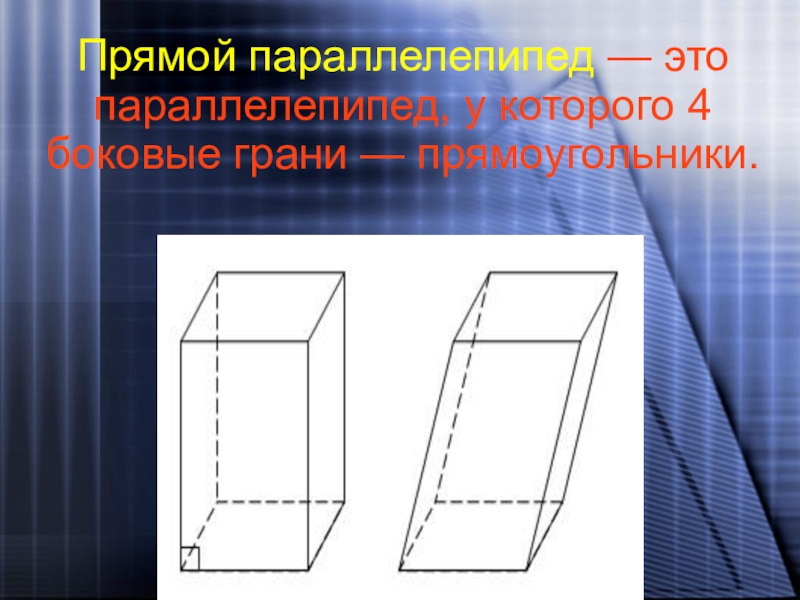
- 21. Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани — прямоугольники.
- 22. Диагонали прямого параллелепипеда вычисляются по формулам:
- 23. Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основанию.
- 24. Куб — это прямоугольный параллелепипед с равными измерениями. Все шесть граней куба — равные квадраты.
- 25. Свойства куба.1.Четыре сечения куба являются правильными шестиугольниками
- 26. Диагональю куба- называют отрезок, соединяющий две вершины,
- 27. В свое время, в1919 году, Чарльз Форт
- 28. Сайты с информацией: http://www.fmclass.ru/math.php?id=4862626930263 http://ru.wikipedia.org http://www.fxyz.ru
- 29. Спасибо за внимание.
Развитие геометрии.Начало геометрии было положено в древности при решении чисто практических задач. Со временем, когда накопилось большое количество геометрических фактов, у людей появилось потребность обобщения, уяснения зависимости одних элементов от других, установления логических связей и доказательств.
Слайд 1Презентация на тему:
«Параллелепипед»
Выполнила :ученица 11класса
МБОУСОШ№7 Гвоздюк Алена.
Учитель :Залова Лена Сафарбей
Слайд 2Развитие геометрии.
Начало геометрии было положено в древности при решении чисто практических
задач. Со временем, когда накопилось большое количество геометрических фактов, у людей появилось потребность обобщения, уяснения зависимости одних элементов от других, установления логических связей и доказательств. Постепенно создавалась геометрическая наука. Примерно в VI - V вв. до н. э. в Древней Греции в геометрии начался новый этап развития.Произведения, содержащие систематическое изложение геометрии, появились в Греции еще в V до н.э., но они были вытеснены "Началами" Евклида.Геометрические знания примерно в объеме современного курса средней школы были изложены еще 2200 лет назад в "Началах" Евклида.
Слайд 3В XVII в. Декарт благодаря методу координат сделал возможным изучение свойств
геометрических фигур с помощью алгебры. С этого времени начала развиваться аналитическая геометрия.
В настоящее время геометрия тесно переплетается со многими другими разделами математики. Одним из источников развития и образования новых понятий в геометрии, как и в других областях математики, являются современные задачи естествознания, физики и техники.
В настоящее время геометрия тесно переплетается со многими другими разделами математики. Одним из источников развития и образования новых понятий в геометрии, как и в других областях математики, являются современные задачи естествознания, физики и техники.
Слайд 5
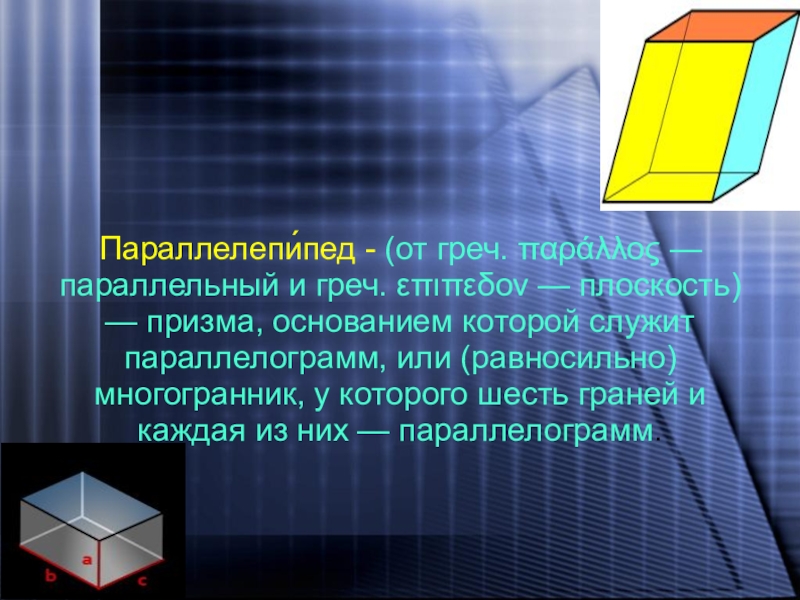
Параллелепи́пед - (от греч. παράλλος — параллельный и греч. επιπεδον —
плоскость) — призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них — параллелограмм.
Слайд 6Основные элементы параллелепипеда:
1.Две грани параллелепипеда, не имеющие общего ребра, называются противоположными,
а имеющие общее ребро — смежными.
2.Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными.
3.Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда.
4.Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями.
2.Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными.
3.Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда.
4.Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями.
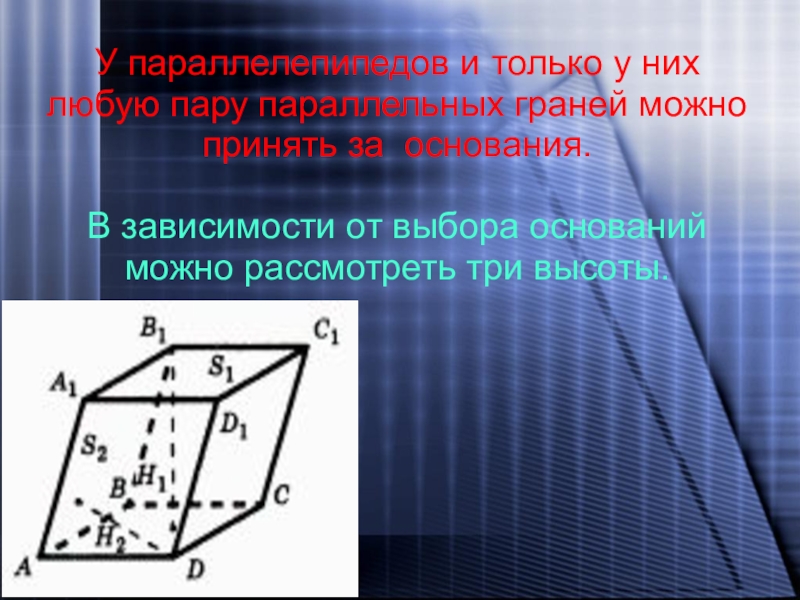
Слайд 7У параллелепипедов и только у них любую пару параллельных граней можно
принять за основания.
В зависимости от выбора оснований можно рассмотреть три высоты.
Слайд 8Свойства параллелепипеда:
1.Противоположные грани параллелепипеда равны и параллельны.
2.Все четыре диагонали параллелепипеда пересекаются
в одной точке и делятся этой точкой пополам.
3.Боковые грани прямого параллелепипеда — прямоугольники.
4.Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
3.Боковые грани прямого параллелепипеда — прямоугольники.
4.Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Слайд 9Теорема:
У параллелепипеда противолежащие грани параллельны и равны.
Доказательство
Возьмем любые две
противолежащие грани параллелепипеда: A1A2A2`A1` и A3A4A4`A3`. Так как все грани параллелепипеда – параллелограммы, то прямая A1A2 параллельна прямой A4A3, а прямая A1A1` параллельна прямой A4A4`. Следовательно плоскости рассматриваемых граней параллельны.
Так как грани параллелепипеда – параллелограммы, то отрезки A1A4, A1`A4`, A2`A3` и A2A3 – параллельны и равны. Следовательно грань A1A2A2`A1` совмещается параллельным переносом вдоль ребра A1A4 с гранью A3A4A4`A3` и, значит, грани равны.
Точно также доказывается параллельность и равенство других противолежащих граней параллелепипеда. Теорема доказана.
Так как грани параллелепипеда – параллелограммы, то отрезки A1A4, A1`A4`, A2`A3` и A2A3 – параллельны и равны. Следовательно грань A1A2A2`A1` совмещается параллельным переносом вдоль ребра A1A4 с гранью A3A4A4`A3` и, значит, грани равны.
Точно также доказывается параллельность и равенство других противолежащих граней параллелепипеда. Теорема доказана.
Слайд 10Теорема: Параллелепипед симметричен относительно середины его диагонали.
Важные свойства параллелепипеда:
1.Любой отрезок с
концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
2. Противолежащие грани параллелепипеда параллельны и равны.
2. Противолежащие грани параллелепипеда параллельны и равны.
Слайд 11Произвольный параллелепипед.
Объём и соотношения в наклонном параллелепипеде часто определяются с помощью
векторной алгебры. Объём параллелепипеда равен абсолютной величине смешанного произведения трёх векторов, определяемых тремя сторонами параллелепипеда, исходящими из одной вершины. Соотношение между длинами сторон параллелепипеда и углами между ними даёт утверждение, что определитель Грама указанных трёх векторов равен квадрату их смешанного произведения
Слайд 13В параллелепипед можно вписать тетраэдр.
Объем такого тетраэдра равен 1/3 части
объема параллелепипеда.
Слайд 15Различается несколько типов параллелепипедов:
1.Прямоугольный параллелепипед.
2.Прямой параллелепипед.
3.Наклонный параллелепипед.
4.Куб.
Слайд 17Вывод формулы объёма прямоугольного параллелепипеда,
измерения которого выражены целыми числами:
Пусть нам
нужно вычислить объём прямоугольного параллелепипеда, длина основания которого равна 20 см, ширина — 12 см и высота параллелепипеда—5 см.
Площадь основания этого параллелепипеда будет равна 20 • 12 = 240 (кв. см). Значит, на его основании в один слой можно уложить 240 кубических сантиметров. Всего таких слоев будет пять. Объём данного параллелепипеда будет равен
240 • 5 = 1200 (куб. см).
Если длину основания прямоугольного параллелепипеда обозначим через а, ширину его — через b и высоту параллелепипеда— через с, то получим формулу:
V = аbс, где V — объём прямоугольного параллелепипеда
Площадь основания этого параллелепипеда будет равна 20 • 12 = 240 (кв. см). Значит, на его основании в один слой можно уложить 240 кубических сантиметров. Всего таких слоев будет пять. Объём данного параллелепипеда будет равен
240 • 5 = 1200 (куб. см).
Если длину основания прямоугольного параллелепипеда обозначим через а, ширину его — через b и высоту параллелепипеда— через с, то получим формулу:
V = аbс, где V — объём прямоугольного параллелепипеда
Слайд 18Свойства диагоналей прямоугольного параллелепипеда:
Диагонали параллелепипеда пересекаются в одной точке и делятся
ею пополам.
Сумма квадратов, диагоналей параллелепипеда равна сумме квадратов всех его ребер.
Сумма квадратов, диагоналей параллелепипеда равна сумме квадратов всех его ребер.
Слайд 19Площадь поверхности прямоугольного параллелепипеда равна удвоенной сумме площадей трех граней этого
параллелепипеда:
S= 2(Sa+Sb+Sc)= 2(ab+ bc+ ac)
Слайд 23Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основанию.
Слайд 24Куб — это прямоугольный параллелепипед с равными измерениями. Все шесть граней
куба — равные квадраты.
Слайд 25Свойства куба.
1.Четыре сечения куба являются правильными шестиугольниками — эти сечения проходят
через центр куба перпендикулярно четырём его главным диагоналям.
2.В куб можно вписать тетраэдр двумя способами. В обоих случаях четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба и все.шесть рёбер тетраэдра будут принадлежать граням куба. В первом случае все вершины тетраэдра принадлежат граням трехгранного угла, вершина которого совпадает с одной из вершин куба. Во втором случае попарно скрещивающиеся ребра тетраэдра принадлежат попарно противолежащим граням куба. Такой тетраэдр является правильным, а его объём составляет 1/3 от объёма куба/
3.В куб можно вписать октаэдр, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.
4.Куб можно вписать в октаэдр, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра.
5.В куб можно вписать икосаэдр, при этом шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра — внутри куба. Все двенадцать вершин икосаэдра будут лежать на шести гранях куба.
2.В куб можно вписать тетраэдр двумя способами. В обоих случаях четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба и все.шесть рёбер тетраэдра будут принадлежать граням куба. В первом случае все вершины тетраэдра принадлежат граням трехгранного угла, вершина которого совпадает с одной из вершин куба. Во втором случае попарно скрещивающиеся ребра тетраэдра принадлежат попарно противолежащим граням куба. Такой тетраэдр является правильным, а его объём составляет 1/3 от объёма куба/
3.В куб можно вписать октаэдр, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.
4.Куб можно вписать в октаэдр, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра.
5.В куб можно вписать икосаэдр, при этом шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра — внутри куба. Все двенадцать вершин икосаэдра будут лежать на шести гранях куба.
Слайд 26Диагональю куба- называют отрезок, соединяющий две вершины, симметричные относительно центра куба.
Диагональ куба находится по формуле , где d — диагональ, а — ребро куба.
Слайд 27В свое время, в1919 году, Чарльз Форт сделал предположение, которое могло
бы объяснить происхождение странной находки, и заключалось оно в том, что «зальцбургский параллелепипед» — это ископаемый артефакт, оставленный представителями иных миров, которые в глубокой древности посещали Землю. Уже в наше время была высказана гипотеза о том, что артефакт — дело рук человека.
«Зальцбургский параллелепипед»