- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Основные понятия и аксиомы стереометрии.
Содержание
- 1. Презентация по математике на тему Основные понятия и аксиомы стереометрии.
- 2. ГЕОМЕТРИЯ возникла из практических задач людей;ГЕОМЕТРИЯ лежит
- 3. Геометрия – одна из самых, а может,
- 4. Древний Египет Древний Египет считается первым государством, оставившим самые ранние математические тексты.
- 5. Что умели древние египтяне1.Умели точно находить площадь
- 6. Первой книгой, содержащей геометрические задачи, считается папирус Райнда, который датируется 9 веком до нашей эры.
- 7. Древняя Греция Пожалуй, дату появления геометрии как
- 8. Древнегреческий ученый Фалес Милетский.Считается одним из первых геометров. Он был причислен к семи мудрецам древности.
- 9. Фалес решил следующие задачи:1. Предложил способ определения
- 10. Школа Евклида Евклид АлександрийскийЯвляется непревзойденным систематизатором, педагогом и популяризатором науки.
- 11. И на рубеже IV и III веков
- 12. Геометрия Лобачевского Геометрия Лобачевского – геометрия Вселенной,
- 13. КУРС ГЕОМЕТРИИПЛАНИМЕТРИЯСТЕРЕОМЕТРИЯ«планиметрия» – наименование смешанного происхождения: от греч.
- 14. ГеометрияПланиметрияСтереометрия stereos - телесный, твердый, объемный, пространственныйmetreo - измерять
- 15. Интуитивное, живое пространственное воображение в сочетании со
- 16. Изучая СТЕРЕОМЕТРИЮ Мы рассмотрим свойства геометрических тел
- 17. Стереометрия.Раздел геометрии, в котором изучаются свойства фигур в пространстве.Основные фигуры в пространстве:АТочка.аПрямая.Плоскость.
- 18. Обозначение основных фигур в пространстве:точкапрямаяплоскостьA, B, C, …a, b, c, …илиAВ, BС, CD, …
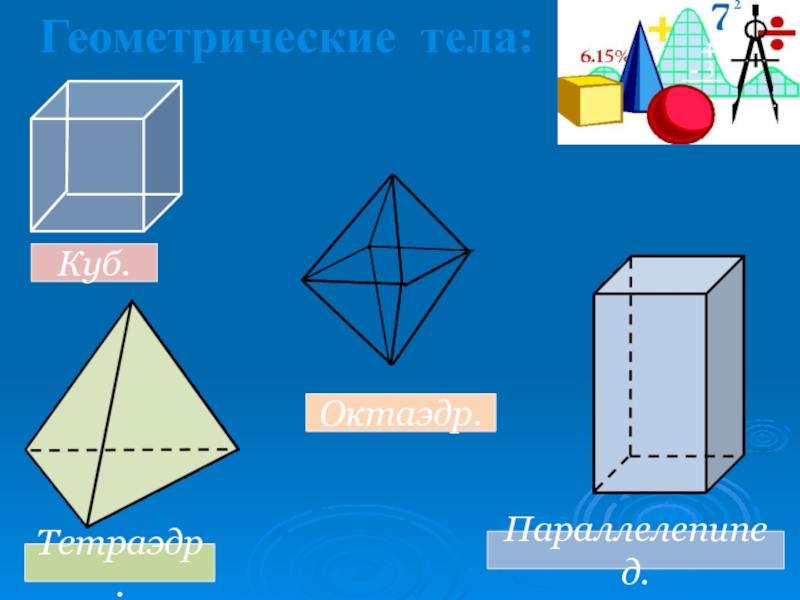
- 19. Геометрические тела:Куб.Параллелепипед.Тетраэдр.Октаэдр.
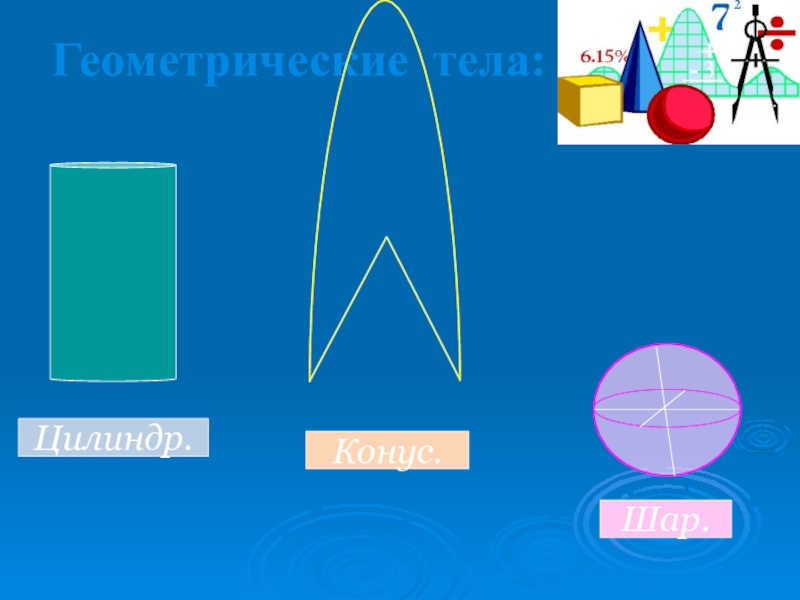
- 20. Геометрические тела:Цилиндр.Конус.Шар.
- 21. Стереометрия широко используется в
- 22. Оперный театр в СиднееДатский архитектор Йорн Утцон был вдохновлён видом парусов.
- 23. Эйфелева башняПариж, Марсово полеИнженер Гюстав Эйфель нашел
- 24. 18000 железных деталей скрепляются 2500000 заклёпками
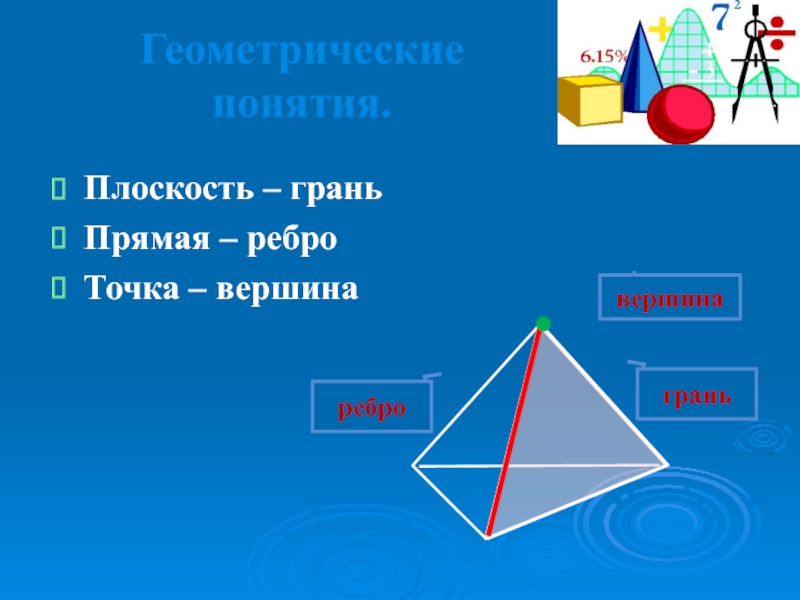
- 25. Геометрические понятия.Плоскость – граньПрямая – реброТочка – вершинавершинаграньребро
- 26. Аксиома(от греч. axíõma – принятие положения)исходное положение научной теории, принимаемое без доказательства
- 27. Аксиомы стереометрии.А1. Через любые три точки, не
- 28. Иллюстрации к аксиоме А1 из жизни.Табурет с
- 29. Аксиомы стереометрии.А2. Если две точки прямой лежат
- 30. Свойство, выраженное в аксиоме А2, используется для
- 31. aА3. Если две плоскости имеют общую точку,
- 32. Слайд 32
- 33. Аксиомы стереометрии описывают:А1.А2. А3. АВСαСпособ задания плоскостиβАВВзаимное расположение прямой и плоскостиВзаимное расположение плоскостейαβ
- 34. Некоторые следствия из аксиом.
- 35. Некоторые следствия из аксиом.
- 36. Взаимное расположение прямой и плоскости.Прямая лежит в
- 37. Решение задач на применение аксиом стереометрии и их следствий.
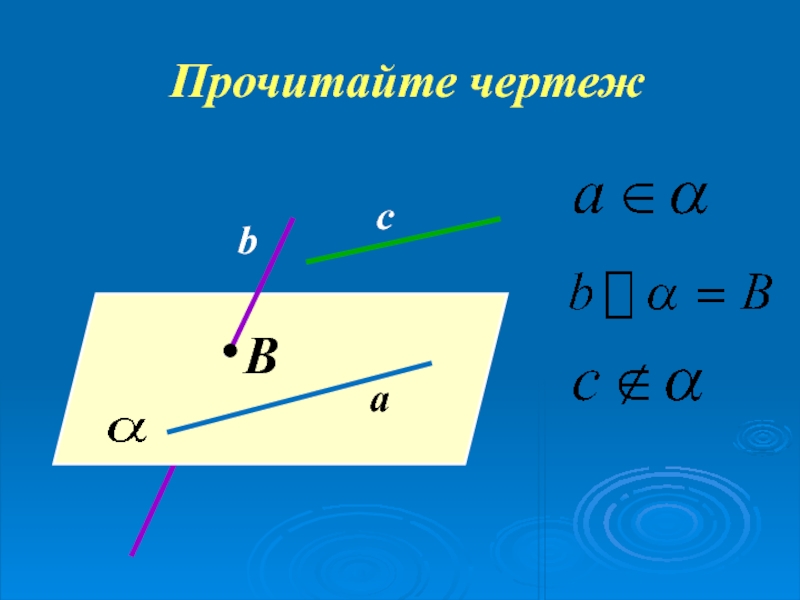
- 38. Прочитайте чертежAС
- 39. Прочитайте чертежBcba
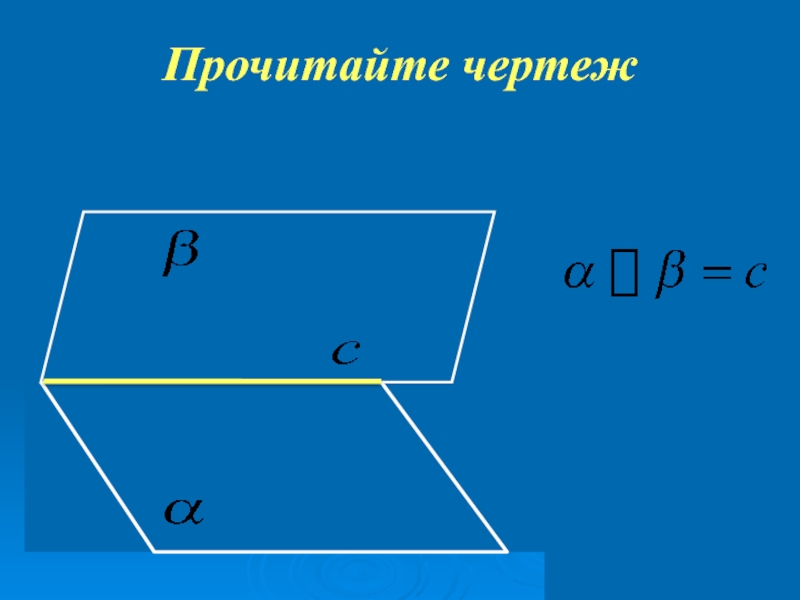
- 40. Прочитайте чертеж
- 41. а) две плоскости, содержащие прямую DE
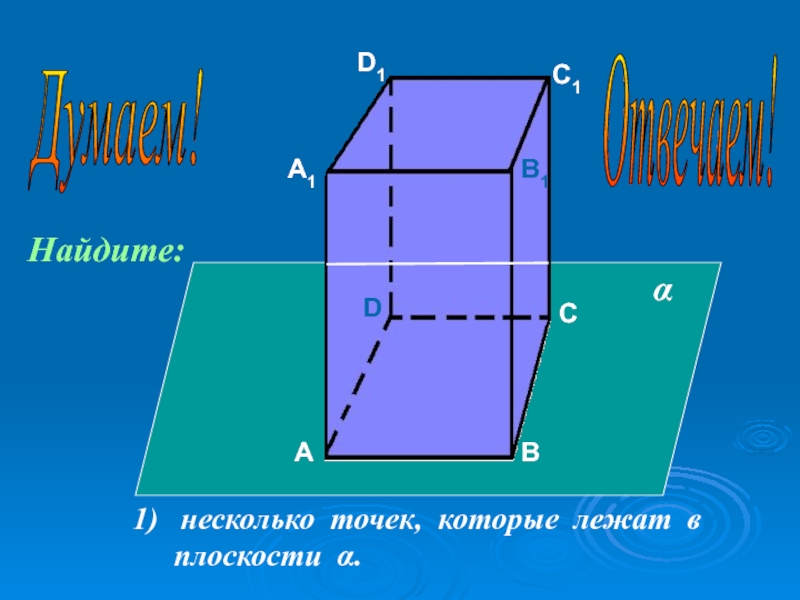
- 42. АА1ВВ1СС1DD1 несколько точек, которые лежат в плоскости α.αНайдите:Думаем! Отвечаем!
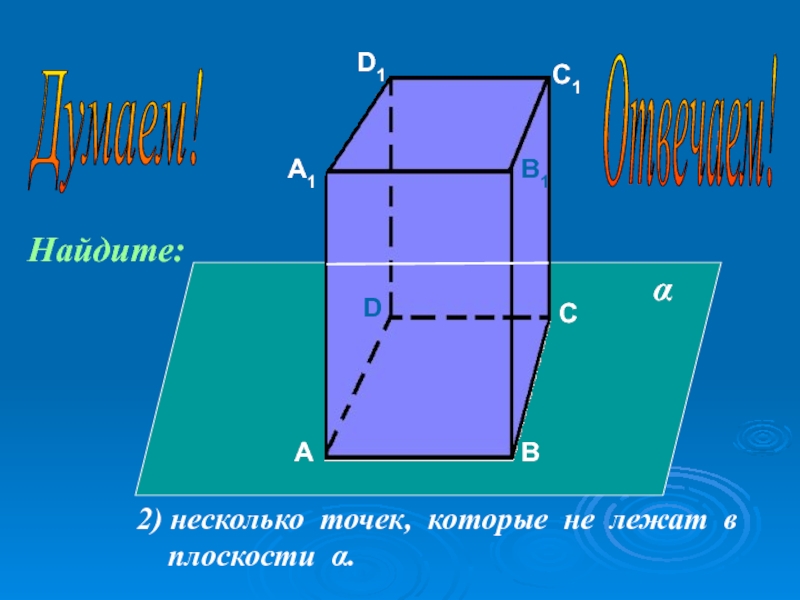
- 43. АА1ВВ1СС1DD12) несколько точек, которые не лежат в плоскости α.αНайдите:Думаем! Отвечаем!
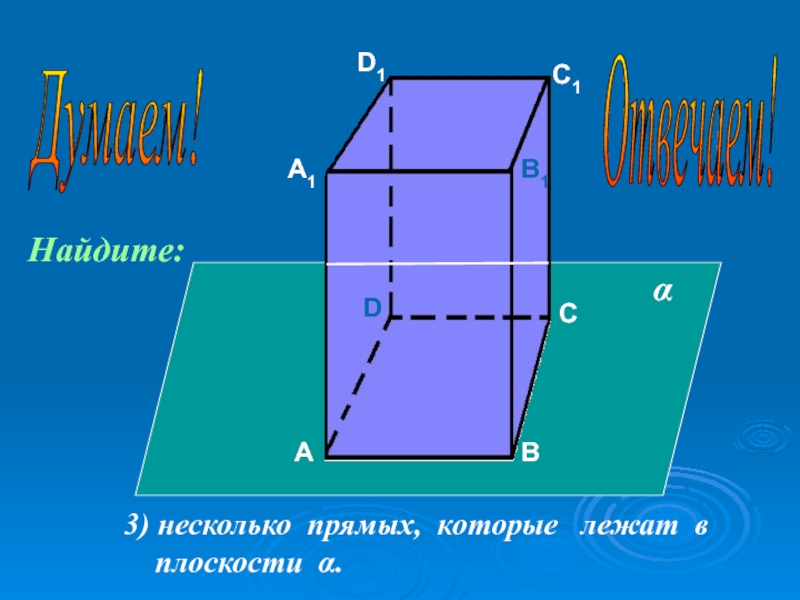
- 44. АА1ВВ1СС1DD13) несколько прямых, которые лежат в плоскости α.αНайдите:Думаем! Отвечаем!
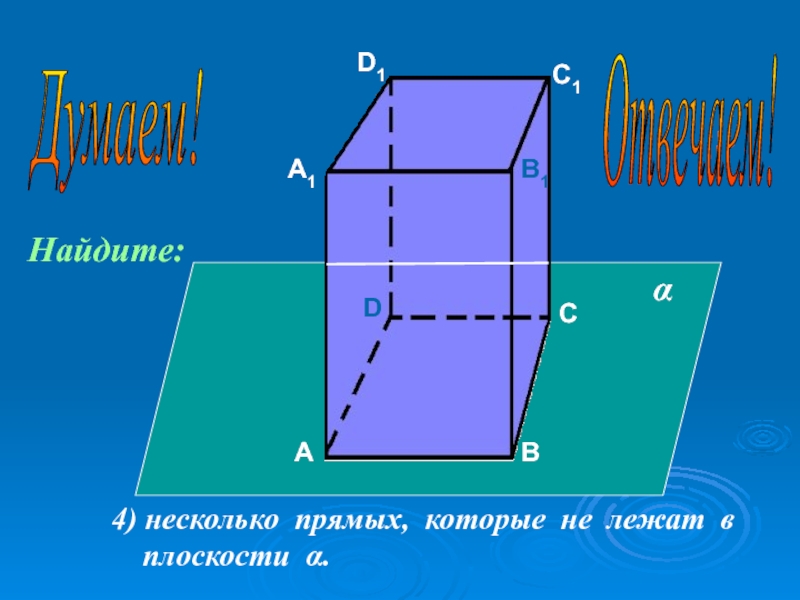
- 45. АА1ВВ1СС1DD14) несколько прямых, которые не лежат в плоскости α.αНайдите:Думаем! Отвечаем!
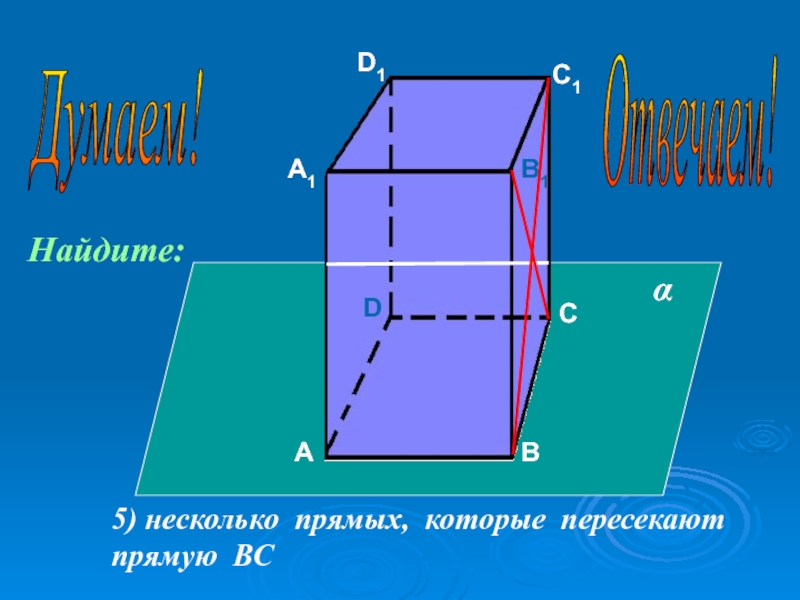
- 46. АА1ВВ1СС1DD15) несколько прямых, которые пересекаютпрямую ВСαНайдите:Думаем! Отвечаем!
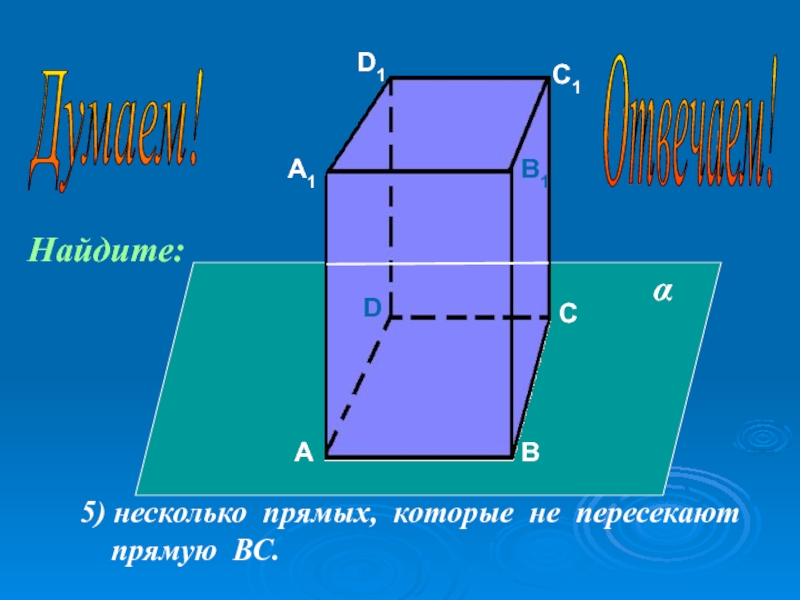
- 47. АА1ВВ1СС1DD15) несколько прямых, которые не пересекают прямую ВС.αНайдите:Думаем! Отвечаем!
- 48. Дан куб АВСDA1B1C1D1.Точка М лежит на ребре
- 49. Дан куб АВСDA1B1C1D1.D1DС1СВ1ВА1АMТочка М лежит на ребре
- 50. Дан куб АВСDA1B1C1D1.D1DС1СВ1ВА1АMТочка М лежит на ребре
- 51. Дан куб АВСDA1B1C1D1.D1DС1СВ1ВА1АMТочка М лежит на ребре
- 52. Д\З: введение, п.1,2,3
Слайд 2ГЕОМЕТРИЯ возникла из практических задач людей;
ГЕОМЕТРИЯ лежит в основе всей техники
ГЕОМЕТРИЯ нужна
технику,
инженеру,
рабочему,
архитектору,
модельеру …
Слайд 3
Геометрия – одна из самых, а может, самая древняя наука, ее
Давайте совершим маленькое путешествие
во времени
Слайд 4Древний Египет
Древний Египет считается первым государством, оставившим самые ранние математические
Слайд 5Что умели древние египтяне
1.Умели точно находить площадь поля треугольной, прямоугольной, трапециевидной
2. Умели строить прямоугольный треугольник при помощи веревки, разделенной узлами на 12 равных частей
3. Знали, что отношение длины окружности к диаметру - число постоянное, приближенное значение этого числа – 3,14.
4. Среди пространственных тел самым египетским можно считать пирамиду, ведь именно такую форму имеют знаменитые усыпальницы фараонов, хотя довольно близко египтяне знакомы с кубом и параллелепипедом
5.Умели вычислять объем усеченной пирамиды, в основании которой квадраты.
Слайд 6Первой книгой, содержащей геометрические задачи, считается папирус Райнда, который датируется 9
Слайд 7Древняя Греция
Пожалуй, дату появления геометрии как науки, можно определить довольно
Слайд 8
Древнегреческий ученый Фалес Милетский.
Считается одним из первых геометров. Он был
Слайд 9Фалес решил следующие задачи:
1. Предложил способ определения расстояния до корабля на
2. Вычислил высоту египетской пирамиды Хеопса по длине отбрасываемой тени.
3. Доказал равенство углов при основании равнобедренного треугольника.
4. Ввел понятие движения, в частности поворота.
5. Доказал второй признак равенства треугольников и впервые применил его в задаче.
6. Теорема Фалеса о равных отрезках, отсекаемых параллельными прямыми на сторонах угла.
Слайд 10Школа Евклида
Евклид Александрийский
Является непревзойденным систематизатором, педагогом и популяризатором науки.
Слайд 11
И на рубеже IV и III веков Евклид создал 13-томный труд,
Эта книга была переведена на языки многих народов мира, а сама геометрия изложенная в ней, стала называться евклидовой геометрией.
Слайд 12Геометрия Лобачевского
Геометрия Лобачевского – геометрия Вселенной, геометрия бесконечного пространства, таящая
Лобачевский Н. И.
Слайд 13КУРС ГЕОМЕТРИИ
ПЛАНИМЕТРИЯ
СТЕРЕОМЕТРИЯ
«планиметрия» – наименование смешанного происхождения: от греч. metreo – измерять
и
«стереометрия» – от греч. stereos – пространственный (stereon – объем).
на плоскости
в пространстве
Изучение свойств геометрических тел
Слайд 14Геометрия
Планиметрия
Стереометрия
stereos - телесный, твердый, объемный, пространственный
metreo - измерять
Слайд 15
Интуитивное, живое пространственное воображение в сочетании со строгой логикой мышления —
ВЫВОД:
При изучении стереометрии мы будем пользоваться рисунками, чертежами: они помогут нам понять, представить, содержание того или иного факта.
Поэтому прежде, чем приступить к пониманию сущности аксиомы, определения, доказательству теоремы, решению геометрической задачи, нужно наглядно представить, вообразить, нарисовать фигуры, о которых идет речь .
«Мой карандаш, бывает еще остроумней моей головы», — признавался великий математик Леонард Эйлер (1707—1783).
Слайд 16Изучая СТЕРЕОМЕТРИЮ
Мы рассмотрим свойства геометрических тел в пространстве.
Освоим различные способы
При этом мы будем развивать пространственное воображение и логическое мышление
Слайд 17
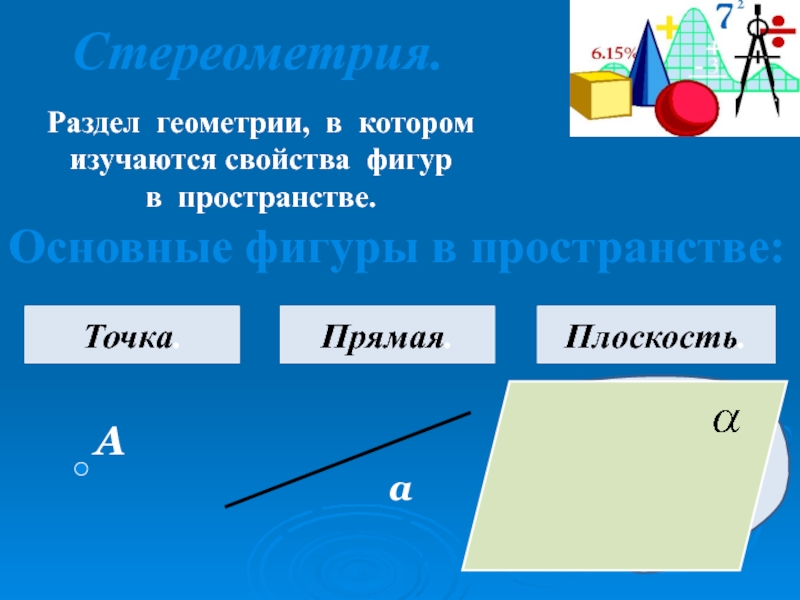
Стереометрия.
Раздел геометрии, в котором
изучаются свойства фигур
в пространстве.
Основные фигуры в
А
Точка.
а
Прямая.
Плоскость.
Слайд 18Обозначение основных
фигур в пространстве:
точка
прямая
плоскость
A, B, C, …
a, b, c, …
или
AВ,
Слайд 21 Стереометрия широко используется в строительном деле, архитектуре, машиностроении,
При
проектировании
этой машины важно было получить такую форму, чтобы при движении сопротивление воздуха было минимально.
Слайд 23Эйфелева башня
Париж, Марсово поле
Инженер Гюстав Эйфель нашел необычную форму для своего
Эйфелева башня весьма устройчива: сильный ветер отклоняет ее вершину всего лишь на 10-12 см. В жару от неравномерного нагревания солнечными лучами она может отклониться на 18 см.
Слайд 26Аксиома
(от греч. axíõma – принятие положения)
исходное положение научной теории, принимаемое без
Слайд 27
Аксиомы стереометрии.
А1. Через любые три точки, не лежащие на одной прямой,
α
А
В
С
Слайд 28
Иллюстрации к аксиоме А1 из жизни.
Табурет с тремя ножками всегда идеально
Для видеокамеры, фотосъемки и для других приборов часто используют штатив – треногу. Три ножки штатива устойчиво расположатся на любом полу в помещениях, на асфальте или прямо на газоне на улице, на песке на пляже или в траве в лесу. Три ножки штатива всегда найдут плоскость.
Слайд 29Аксиомы стереометрии.
А2. Если две точки прямой лежат в плоскости, то все
α
А
В
Слайд 30Свойство, выраженное в аксиоме А2, используется для проверки «ровности» чертежной линейки.
Слайд 31
a
А3. Если две плоскости имеют общую точку, то они
В этом случае говорят, что плоскости пересекаются по прямой.
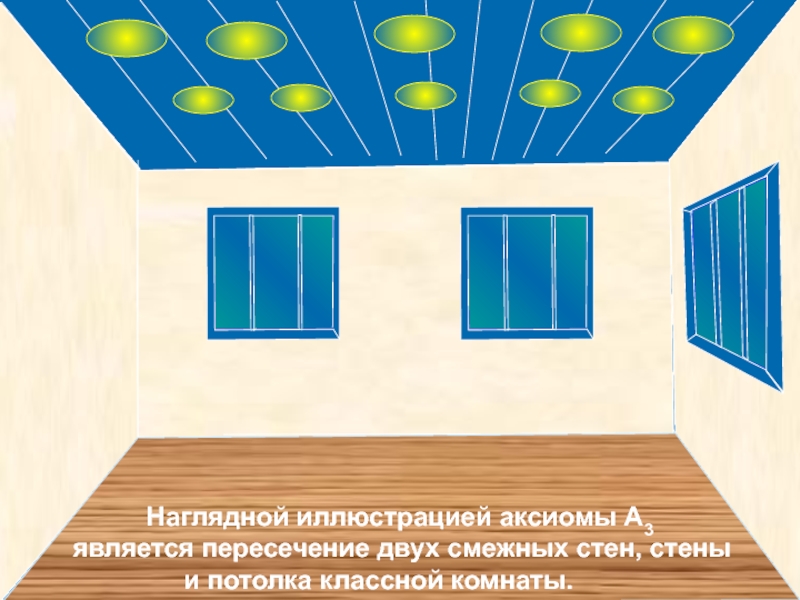
Слайд 32
Наглядной иллюстрацией
является пересечение двух смежных стен, стены
и потолка классной комнаты.
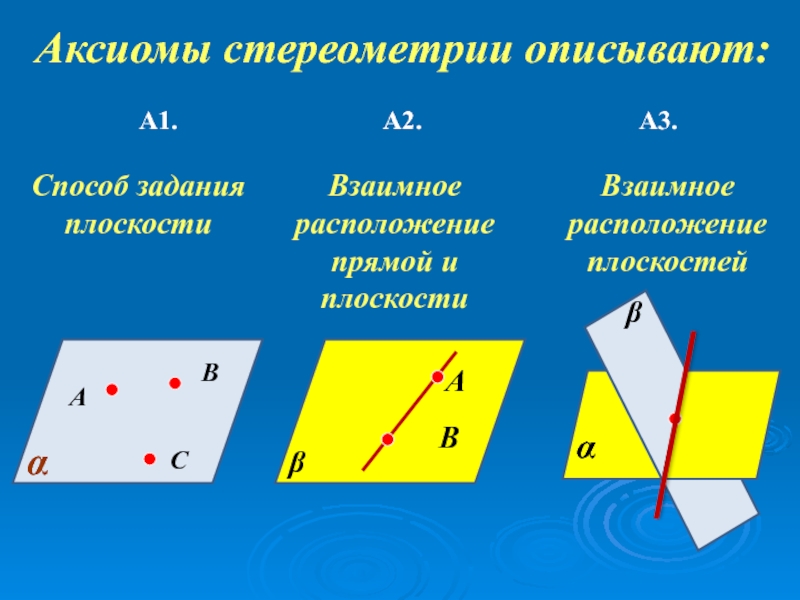
Слайд 33
Аксиомы стереометрии описывают:
А1.
А2.
А3.
А
В
С
α
Способ задания плоскости
β
А
В
Взаимное расположение прямой и плоскости
Взаимное
α
β
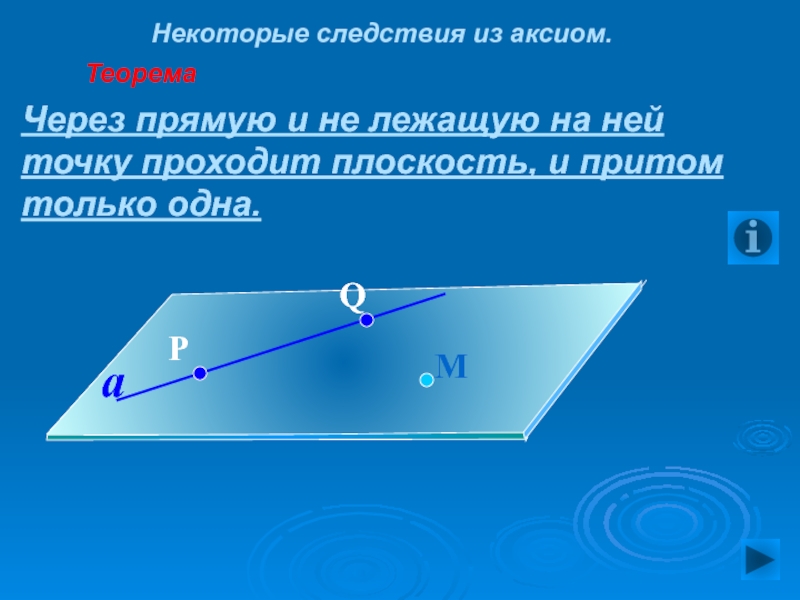
Слайд 34 Некоторые следствия из аксиом.
Теорема
Через прямую
М
a
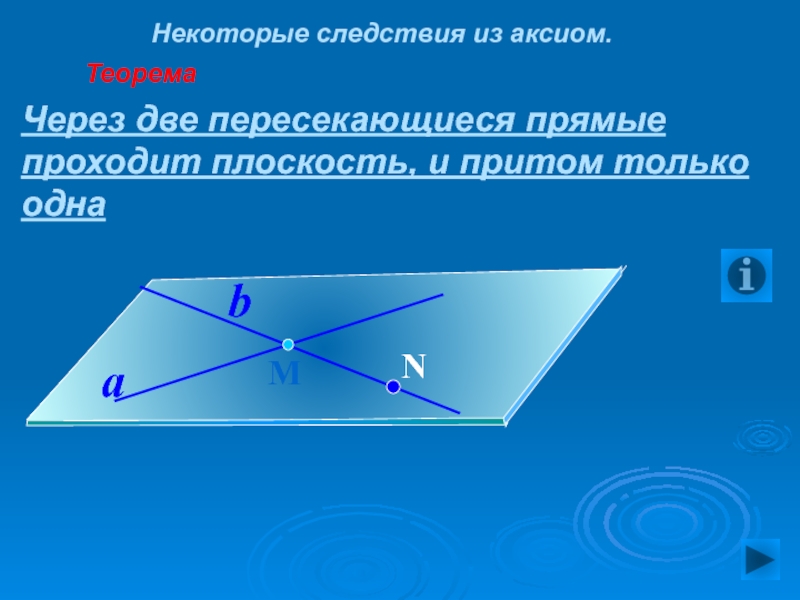
Слайд 35 Некоторые следствия из аксиом.
Теорема
Через две
М
a
b
N
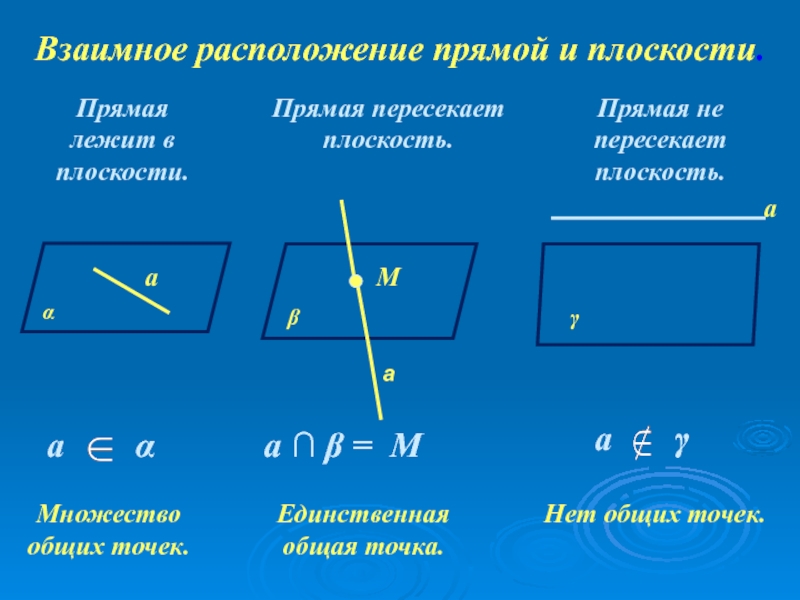
Слайд 36Взаимное расположение прямой и плоскости.
Прямая лежит в плоскости.
Прямая пересекает плоскость.
Прямая не
Множество общих точек.
Единственная общая точка.
Нет общих точек.
α
а
β
а
М
γ
а
а α
а ∩ β = М
а γ
Слайд 41
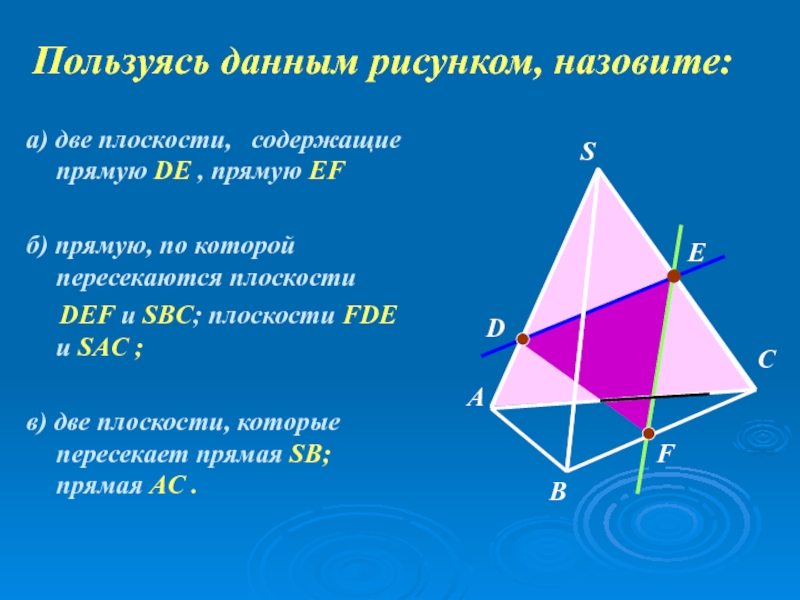
а) две плоскости, содержащие прямую DE , прямую EF
б) прямую,
DEF и SBC; плоскости FDE и SAC ;
в) две плоскости, которые пересекает прямая SB; прямая AC .
Пользуясь данным рисунком, назовите:
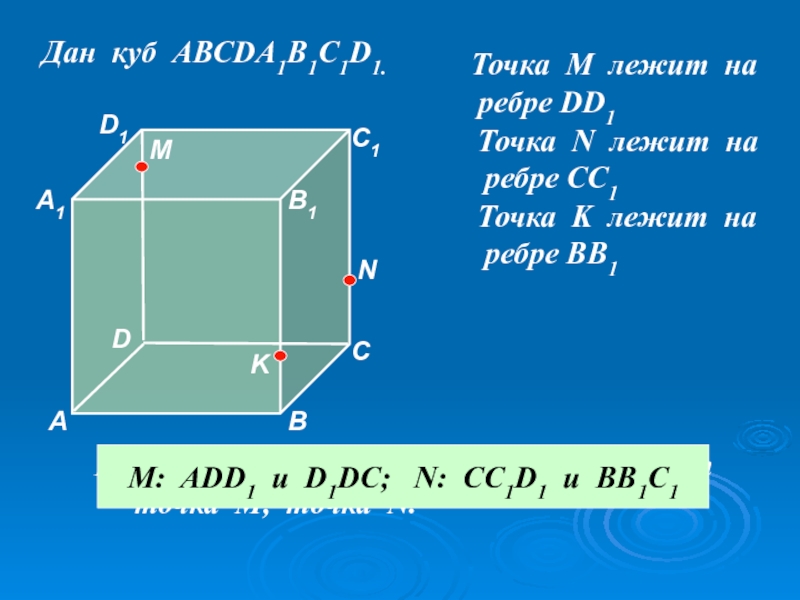
Слайд 48Дан куб АВСDA1B1C1D1.
Точка М лежит на
ребре DD1
Точка N лежит
ребре CC1
Точка K лежит на
ребре BB1
D1
В
А1
А
D
С1
С
В1
M
N
K
Назовите плоскости в которых лежат
точка М, точка N.
M: ADD1 и D1DC; N: CC1D1 и BB1C1
Слайд 49
Дан куб АВСDA1B1C1D1.
D1
D
С1
С
В1
В
А1
А
M
Точка М лежит на
ребре DD1
N
Точка N лежит
ребре CC1
K
Точка K лежит на
ребре BB1
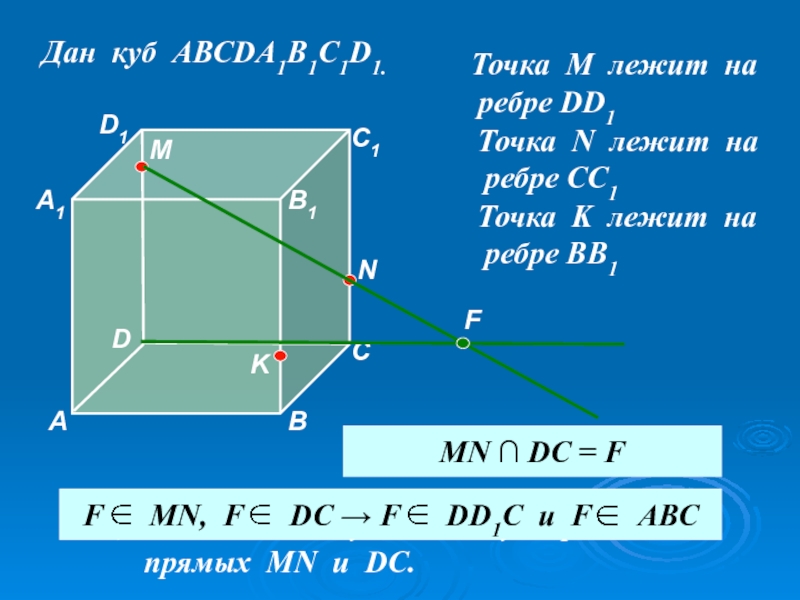
2) Найдите точку F – точку пересечения
прямых MN и DС.
F
Каким свойством обладает точка F?
MN ∩ DC = F
F MN, F DC → F DD1C и F АВС
Слайд 50
Дан куб АВСDA1B1C1D1.
D1
D
С1
С
В1
В
А1
А
M
Точка М лежит на
ребре DD1
N
Точка N лежит
ребре CC1
K
Точка K лежит на
ребре BB1
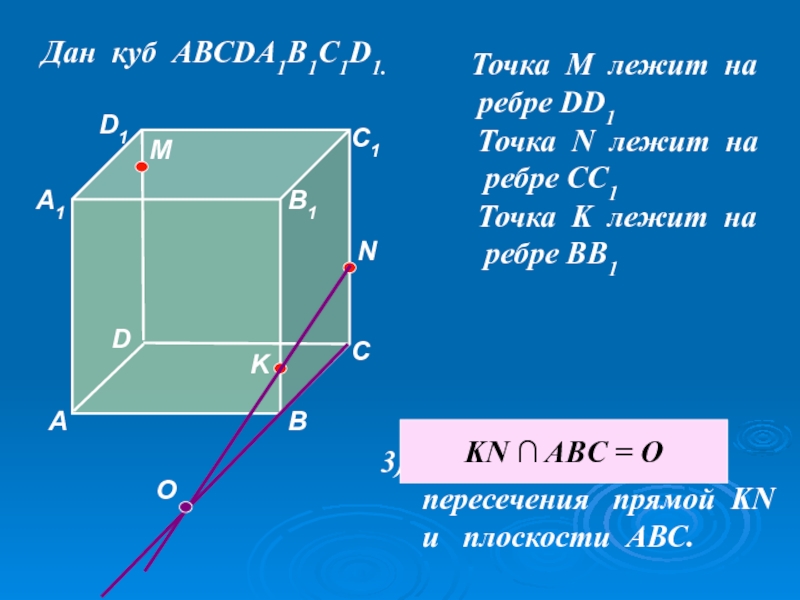
Найдите точку
пересечения прямой KN
и плоскости АВС.
О
KN ∩ ABC = O
Слайд 51
Дан куб АВСDA1B1C1D1.
D1
D
С1
С
В1
В
А1
А
M
Точка М лежит на
ребре DD1
N
Точка N лежит
ребре CC1
K
Точка K лежит на
ребре BB1
O
F
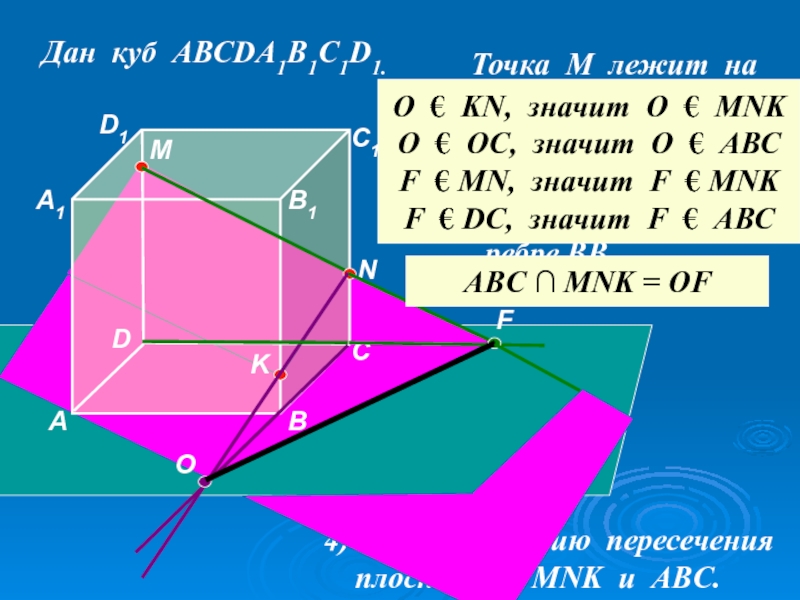
4) Найдите линию пересечения
плоскостей MNK и ABC.
ABC ∩ MNK = OF
O € KN, значит О € МNK
O € OC, значит О € АВС
F € MN, значит F € MNK
F € DC, значит F € АВС