- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему несколько способов решения одной задачи
Содержание
- 1. Презентация по математике на тему несколько способов решения одной задачи
- 2. ВАЕDCДано: ∆ ABC,ВЕ-биссектриса,АD- медиана, ВЕ
- 3. ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛРавенство прямоугольных треугольниковСвойство равнобедренного треугольникаСвойство точки пересечения медианСвойство средней линии треугольникаТеорема Пифагора
- 4. В ∆ ABC биссектриса BE и медиана
- 5. ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛСвойство равнобедренного треугольникаСвойство биссектрисы треугольникаСвойство средней линии треугольникаТеорема Пифагора
- 6. В ∆ ABC биссектриса BE и
- 7. ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛФормулы площадей треугольников Свойство аддитивности площадей
- 8. СПАСИБО ЗА ВНИМАНИЕ!!!
Слайд 2В
А
Е
D
C
Дано: ∆ ABC,ВЕ-биссектриса,
АD- медиана, ВЕ АD. ВЕ= АD
Найти: АВ, ВС, АС.
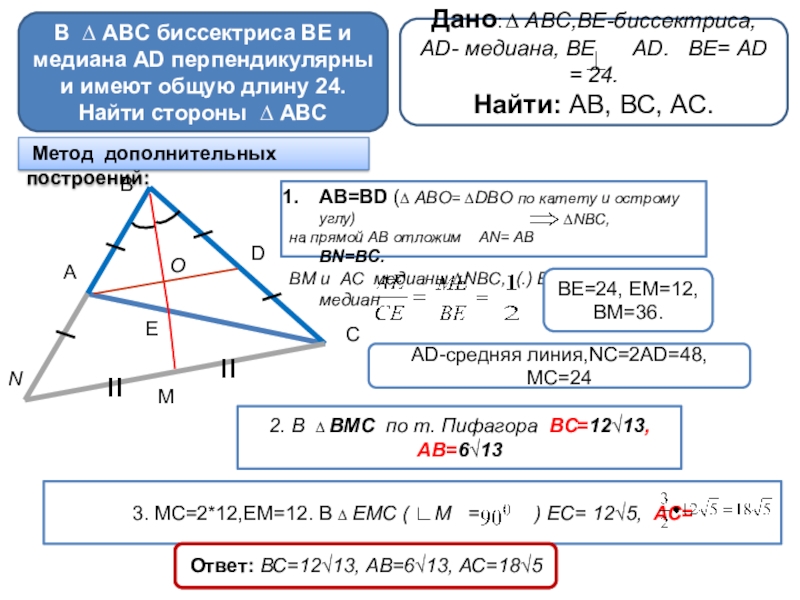
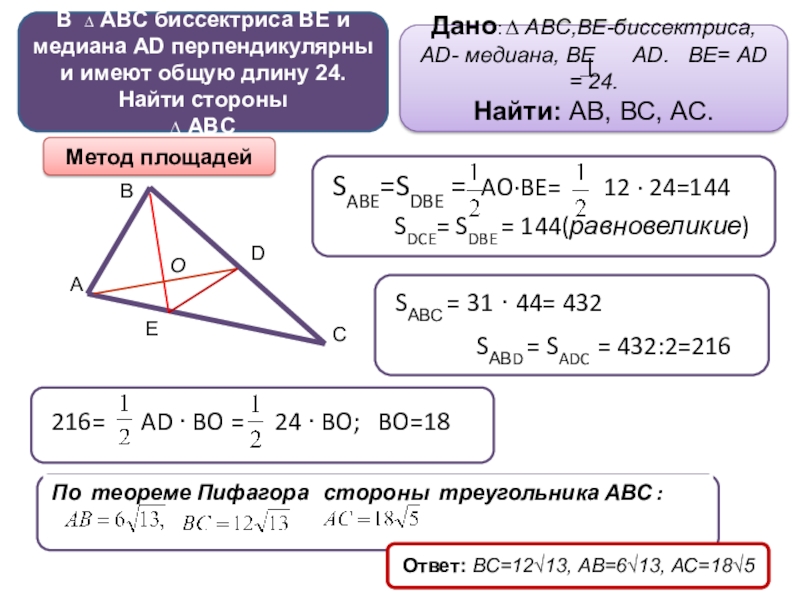
В ∆ ABC биссектриса BE и медиана AD перпендикулярны и имеют общую длину 24.Найти стороны ∆ ABC
Метод дополнительных построений:
АВ=ВD (∆ АВО= ∆DВО по катету и острому углу)
на прямой АВ отложим АN= АВ ВN=ВС.
ВМ и АС медианы ∆NВС, (.) Е –пересечения медиан
О
N
∆NВС,
М
=
=
ВЕ=24, ЕМ=12,ВМ=36.
АD-средняя линия,NC=2АD=48, МС=24
2. В ∆ ВМС по т. Пифагора ВС=12√13, АВ=6√13
3. МС=2*12,ЕМ=12. В ∆ ЕМС ( ∟М = ) ЕС= 12√5, АС=
Ответ: ВС=12√13, АВ=6√13, АС=18√5
Слайд 3ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
Равенство прямоугольных треугольников
Свойство равнобедренного треугольника
Свойство точки пересечения медиан
Свойство средней линии
Теорема Пифагора
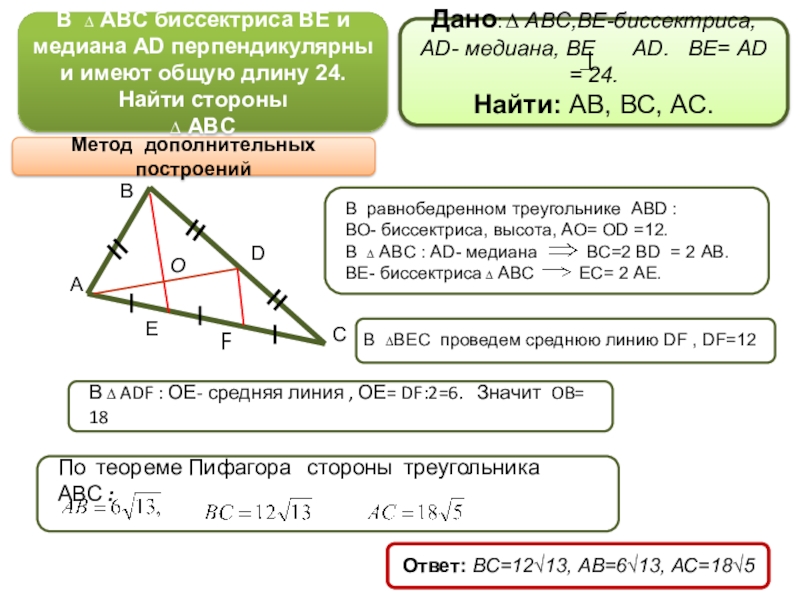
Слайд 4В ∆ ABC биссектриса BE и медиана AD перпендикулярны и имеют
∆ ABC
Дано: ∆ ABC,ВЕ-биссектриса,
АD- медиана, ВЕ АD. ВЕ= АD = 24.
Найти: АВ, ВС, АС.
В равнобедренном треугольнике АВD : ВО- биссектриса, высота, АО= OD =12
В равнобедренном треугольнике АВD :
ВО- биссектриса, высота, АО= OD =12.
В ∆ ABC : АD- медиана ВС=2 ВD = 2 АВ. ВЕ- биссектриса ∆ ABC ЕС= 2 АЕ.
Метод дополнительных построений
В
D
А
О
Е
C
F
=
=
=
В ∆ВЕС проведем среднюю линию DF , DF=12
В ∆ ADF : ОЕ- средняя линия , ОЕ= DF:2=6. Значит OB= 18
По теореме Пифагора стороны треугольника АВС :
Ответ: ВС=12√13, АВ=6√13, АС=18√5
Слайд 5
ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
Свойство равнобедренного треугольника
Свойство биссектрисы треугольника
Свойство средней линии треугольника
Теорема Пифагора
Слайд 6
В ∆ ABC биссектриса BE и медиана AD перпендикулярны и
∆ ABC
Дано: ∆ ABC,ВЕ-биссектриса,
АD- медиана, ВЕ АD. ВЕ= АD = 24.
Найти: АВ, ВС, АС.
Метод площадей
1.SABE=SDBE =AO*BE
В
Е
А
D
C
SABE=SDBE = AO∙BE= 12 ∙ 24=144
О
SDCE= SDBE = 144(равновеликие)
SАВС = 31 ∙ 44= 432
SАВD = SADC = 432:2=216
216= AD ∙ BO = 24 ∙ BO; BO=18
По теореме Пифагора стороны треугольника АВС :
Ответ: ВС=12√13, АВ=6√13, АС=18√5
Слайд 7ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
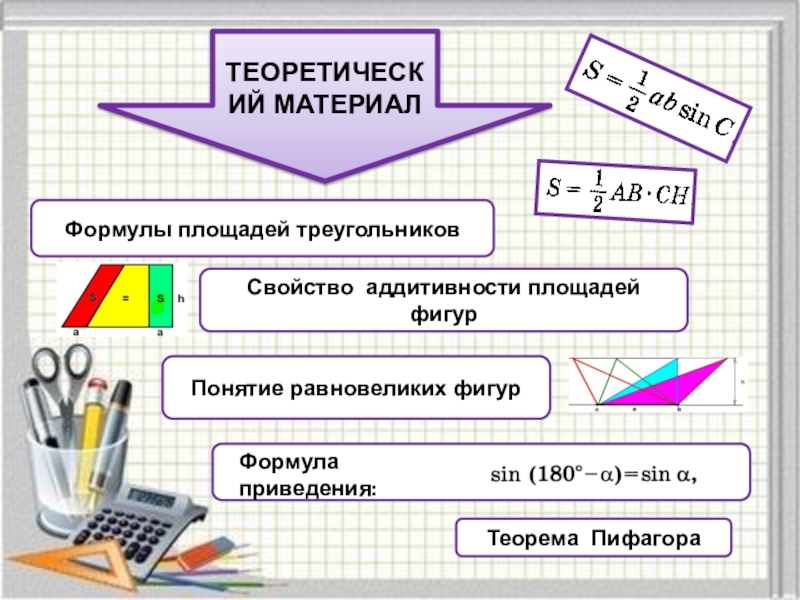
Формулы площадей треугольников
Свойство аддитивности площадей фигур
Понятие равновеликих фигур
Теорема Пифагора
Формула приведения: