- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Неевклидовы геометрии
Содержание
- 1. Презентация по математике на тему Неевклидовы геометрии
- 2. В геометрии истинность каждого утверждения необходимо доказывать,
- 3. В основе всей геометрии греческого математика Евклида
- 4. 4 постулата Евклида
- 5. Первые 4 аксиомы не вызывали сомнений ни
- 6. Евклид Через точку, не лежащую на прямой, можно провести только одну прямую, параллельную данной.
- 7. Эта аксиома вызывала особый интерес математиков. В
- 8. Это не удалось никому. Поэтому возникла мысль:
- 9. Лобачевский Через точку, не лежащую на прямой, можно провести как минимум две прямые, параллельные данной.
- 10. «Коперник» геометрииВеличайшим научным подвигом Николая Лобачевского считается создание им
- 11. Профессор Казанского университета Н.И. Лобачевский построил новую
- 12. ПсевдосфераВ геометрии Лобачевского подобных фигур не существует
- 13. В геометрии Лобачевского сохраняются все теоремы, которые
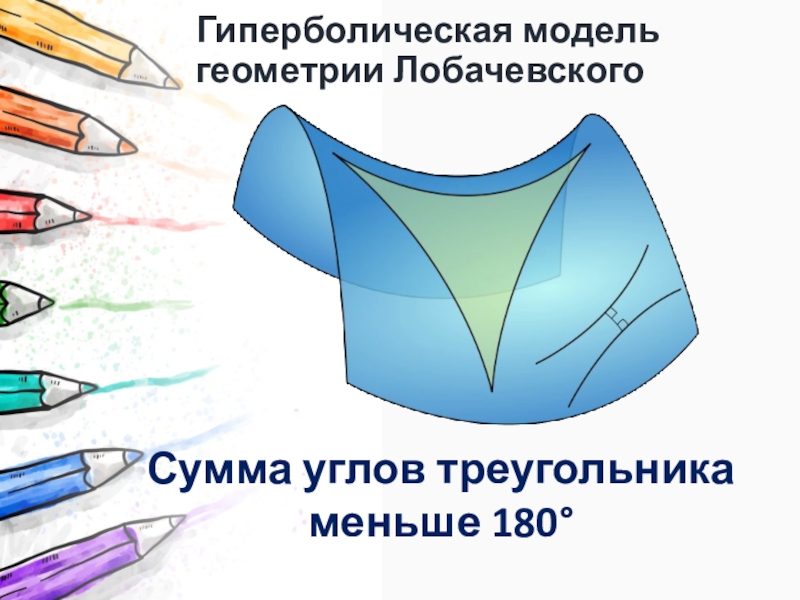
- 14. Гиперболическая модель геометрии ЛобачевскогоСумма углов треугольникаменьше 180
- 15. Теорема о сумме углов треугольника готовит первый
- 16. Некоторые теоремы геометрии ЛобачевскогоДва неравных равносторонних треугольника
- 17. Риман Через точку, не лежащую на
- 18. Развитие других геометрийЧерез некоторое время идеи Лобачевского
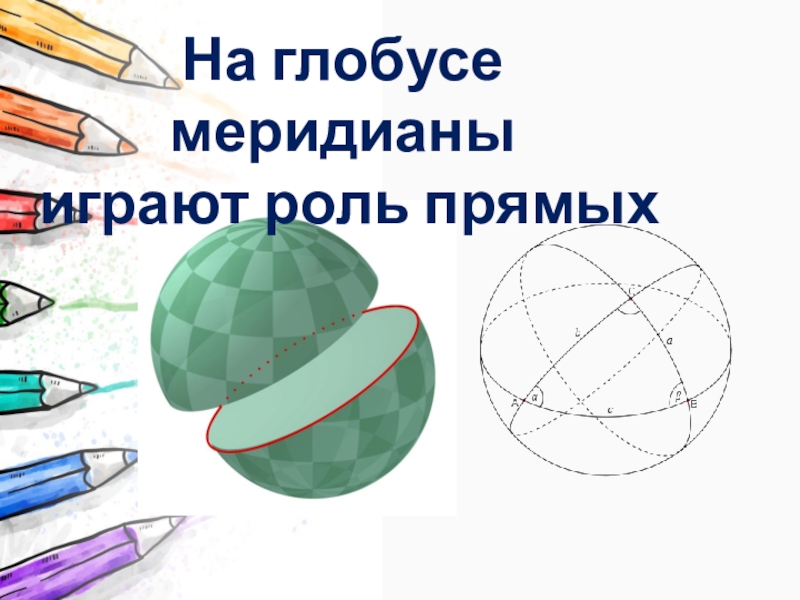
- 19. На глобусе меридианыиграют роль прямых
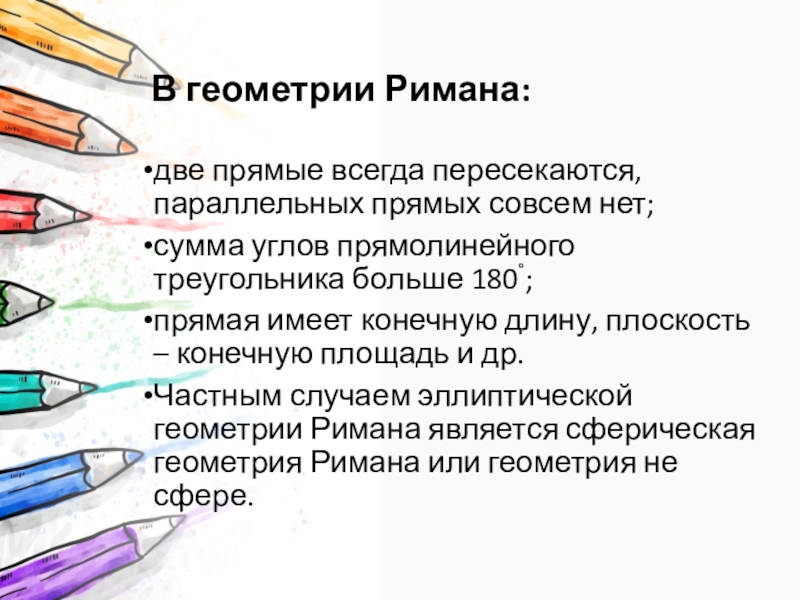
- 20. В геометрии Римана:две прямые всегда пересекаются, параллельных
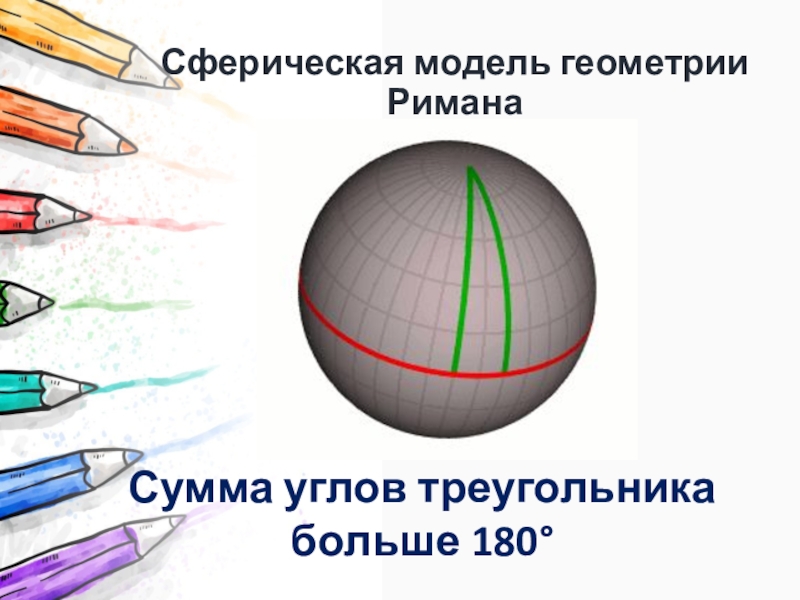
- 21. Сферическая модель геометрии РиманаСумма углов треугольникабольше 180
- 22. Через точку, не лежащую на прямой, можно
- 23. Альберт Эйнштейн
- 24. Современники Лобачевского, потом и Римана отказывались принимать
- 25. Тяготение- результат искривления пространства вблизи массивных тел
В геометрии истинность каждого утверждения необходимо доказывать, нельзя полагаться только на наблюдения.В школьном курсе геометрии мы пользуемся евклидовской геометрией.
Слайд 2В геометрии истинность каждого утверждения необходимо доказывать, нельзя полагаться только на
наблюдения.
В школьном курсе геометрии мы пользуемся евклидовской геометрией.
В школьном курсе геометрии мы пользуемся евклидовской геометрией.
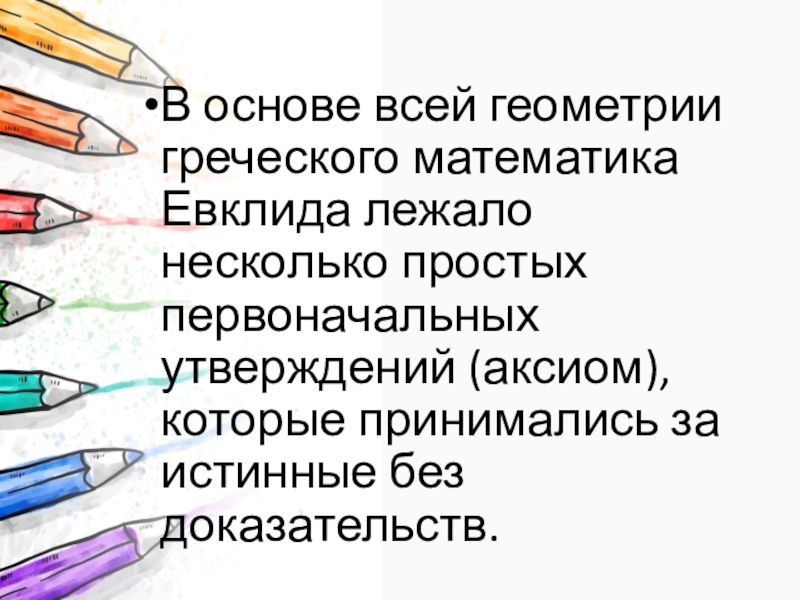
Слайд 3В основе всей геометрии греческого математика Евклида лежало несколько простых первоначальных
утверждений (аксиом), которые принимались за истинные без доказательств.
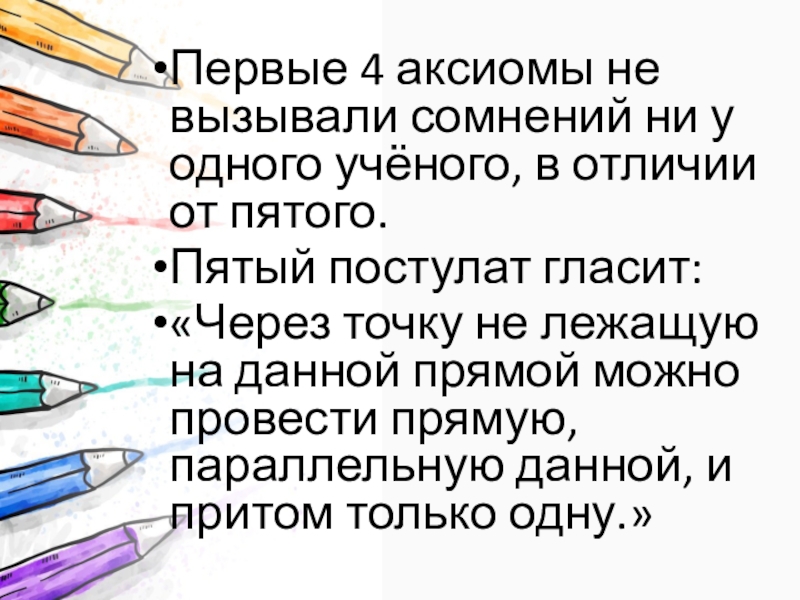
Слайд 5Первые 4 аксиомы не вызывали сомнений ни у одного учёного, в
отличии от пятого.
Пятый постулат гласит:
«Через точку не лежащую на данной прямой можно провести прямую, параллельную данной, и притом только одну.»
Пятый постулат гласит:
«Через точку не лежащую на данной прямой можно провести прямую, параллельную данной, и притом только одну.»
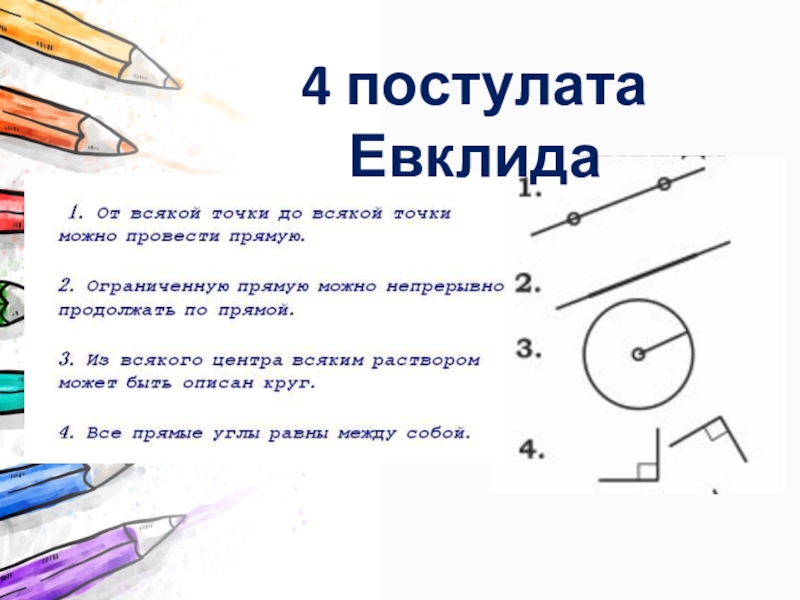
Слайд 6Евклид
Через точку, не лежащую на прямой, можно провести только
одну прямую, параллельную данной.
Слайд 7Эта аксиома вызывала особый интерес математиков. В отличие от остальных аксиом
элементарной геометрии, аксиома параллельных не обладает свойством непосредственной очевидности. Поэтому на всем протяжении истории геометрии имели место попытки доказать аксиому параллельных.
Слайд 8Это не удалось никому. Поэтому возникла мысль: «Не может ли быть
так, что заменив пятый постулат его отрицанием, мы придём к новой неевклидовой геометрии, которая во многом не согласуется с нашими привычными наглядными представлениями, но, тем не менее не содержит никаких логических противоречий?»
Слайд 9Лобачевский
Через точку, не лежащую на прямой, можно провести как
минимум две прямые, параллельные данной.
Слайд 10«Коперник» геометрии
Величайшим научным подвигом Николая Лобачевского считается создание им первой неевклидовой геометрии, историю
которой принято отсчитывать от заседания Отделения физико-математических наук в Казанском университете 11 февраля 1826, на котором Лобачевский выступил с докладом «Сжатое изложение основ геометрии со строгим доказательством теоремы о параллельных».
Ни комиссия, ни другие современники Лобачевского, в том числе выдающийся математик М. В. Остроградский, не смогли по достоинству оценить открытие Лобачевского. Признание пришло лишь через 12 лет после его смерти, когда в 1868 г. Э. Бельтрами показал, что геометрия Лобаческого может быть реализована на псевдосферических поверхностях в евклидовом пространстве, если за прямые принять геодезические.
Ни комиссия, ни другие современники Лобачевского, в том числе выдающийся математик М. В. Остроградский, не смогли по достоинству оценить открытие Лобачевского. Признание пришло лишь через 12 лет после его смерти, когда в 1868 г. Э. Бельтрами показал, что геометрия Лобаческого может быть реализована на псевдосферических поверхностях в евклидовом пространстве, если за прямые принять геодезические.
Слайд 11Профессор Казанского университета Н.И. Лобачевский построил новую геометрию, откинув 5 постулат
Евклида, заменив его другим, прямо противоположным по смыслу:
“Через точку вне прямой в плоскости проходит по крайней мере две прямые не имеющие общей точки с первой прямой”.
Случилось это в 1826 году. Лобачевский не получил противоречия.
“Через точку вне прямой в плоскости проходит по крайней мере две прямые не имеющие общей точки с первой прямой”.
Случилось это в 1826 году. Лобачевский не получил противоречия.
Слайд 13В геометрии Лобачевского сохраняются все теоремы, которые в евклидовой геометрии можно
доказать без использования пятого постулата. Например:
вертикальные углы равны;
углы при основании равнобедренного треугольника равны;
из данной точки можно опустить на данную прямую только один перпендикуляр и др.
вертикальные углы равны;
углы при основании равнобедренного треугольника равны;
из данной точки можно опустить на данную прямую только один перпендикуляр и др.
Слайд 15Теорема о сумме углов треугольника готовит первый “сюрприз”: в геометрии Лобачевского
сумма углов любого треугольника меньше 180°.
Самую большую площадь имеет треугольник с нулевыми углами, а его стороны имеют бесконечную длину.
Самую большую площадь имеет треугольник с нулевыми углами, а его стороны имеют бесконечную длину.
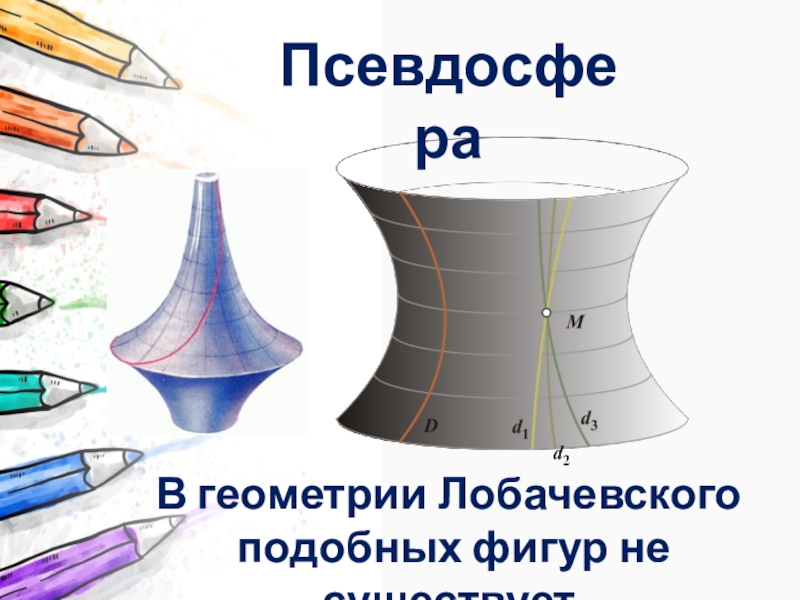
Слайд 16Некоторые теоремы геометрии Лобачевского
Два неравных равносторонних треугольника имеют неравные углы.
В геометрии
Лобачевского не существует подобных фигур.
Если углы одного треугольника равны соответственно углам другого треугольника, то эти треугольники равны.
Если углы одного треугольника равны соответственно углам другого треугольника, то эти треугольники равны.
Слайд 17Риман
Через точку, не лежащую на прямой, нельзя провести ни
одной прямой, параллельной данной. Все прямые пересекаются.
Слайд 18Развитие других геометрий
Через некоторое время идеи Лобачевского были приняты математиками, и
следующим этапом развития геометрии стала эллиптическая геометрия Римана. Риман исходил из того, что через точку, не лежащую на данной прямой, вообще нельзя провести прямую, не пересекающую данную.
Слайд 20В геометрии Римана:
две прямые всегда пересекаются, параллельных прямых совсем нет;
сумма
углов прямолинейного треугольника больше 180°;
прямая имеет конечную длину, плоскость – конечную площадь и др.
Частным случаем эллиптической геометрии Римана является сферическая геометрия Римана или геометрия не сфере.
прямая имеет конечную длину, плоскость – конечную площадь и др.
Частным случаем эллиптической геометрии Римана является сферическая геометрия Римана или геометрия не сфере.
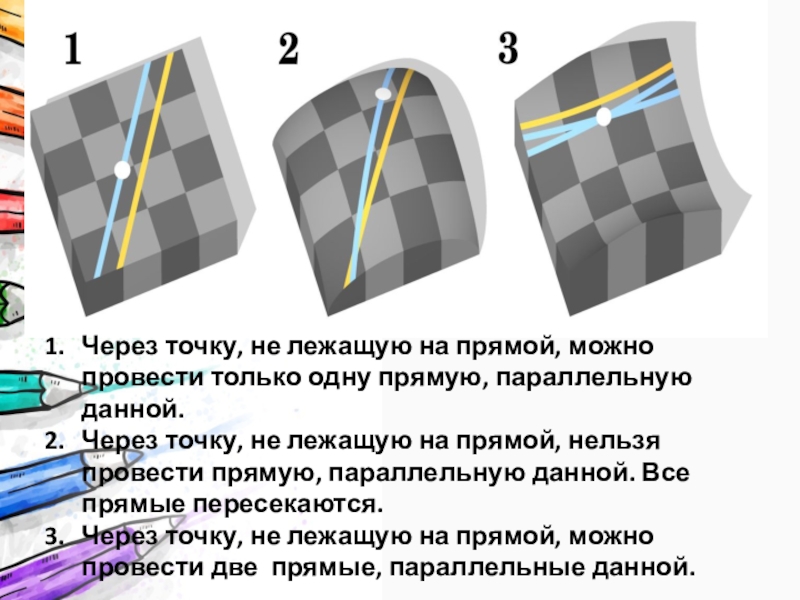
Слайд 22Через точку, не лежащую на прямой, можно провести только одну прямую,
параллельную данной.
Через точку, не лежащую на прямой, нельзя провести прямую, параллельную данной. Все прямые пересекаются.
Через точку, не лежащую на прямой, можно провести две прямые, параллельные данной.
Через точку, не лежащую на прямой, нельзя провести прямую, параллельную данной. Все прямые пересекаются.
Через точку, не лежащую на прямой, можно провести две прямые, параллельные данной.
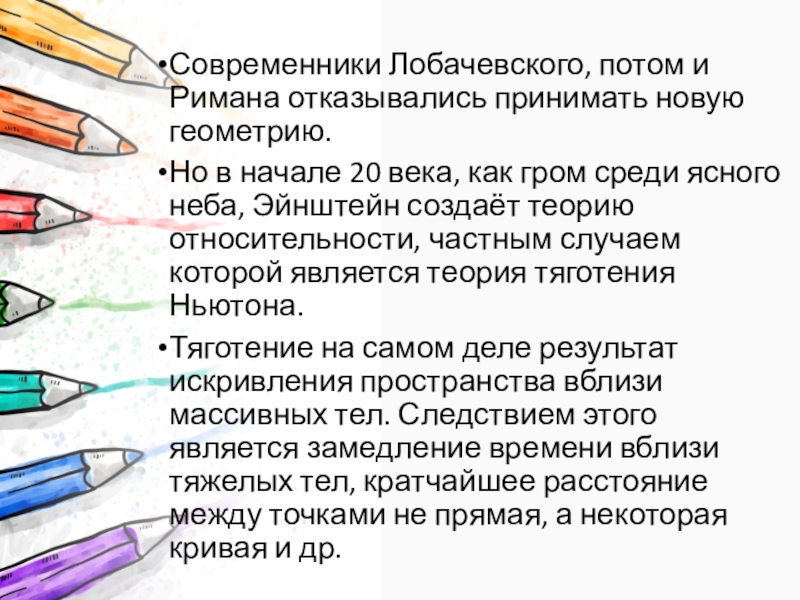
Слайд 24Современники Лобачевского, потом и Римана отказывались принимать новую геометрию.
Но в
начале 20 века, как гром среди ясного неба, Эйнштейн создаёт теорию относительности, частным случаем которой является теория тяготения Ньютона.
Тяготение на самом деле результат искривления пространства вблизи массивных тел. Следствием этого является замедление времени вблизи тяжелых тел, кратчайшее расстояние между точками не прямая, а некоторая кривая и др.
Тяготение на самом деле результат искривления пространства вблизи массивных тел. Следствием этого является замедление времени вблизи тяжелых тел, кратчайшее расстояние между точками не прямая, а некоторая кривая и др.