Для нахождения расстояния от точки А до прямой ɑ сначала находят основание А’ перпендикуляра, опущенного из точки А на прямую ɑ. Если нахождение длины перпендикуляра АА’ не вытекает непосредственно из условия задачи, то на прямой ɑ выбирают какие-нибудь точки В, С и рассматривают треугольник АВС, в котором АА’ является высотой (рис. 2). Для нахождения высоты АА’ используют теорему Пифагора или другие теоремы и формулы.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Нахождение расстояния от точки до прямой и между скрещивающимися прямымик учебнику геометрии авторов И.М.Смирнова, В.А.Смирнов
Содержание
- 1. Презентация по математике на тему Нахождение расстояния от точки до прямой и между скрещивающимися прямымик учебнику геометрии авторов И.М.Смирнова, В.А.Смирнов
- 2. 1. В единичном кубе АВСDA1В1С1D1 найдите
- 3. 2’. В единичном кубе АВСDA1В1С1D1 найдите
- 4. 3. В единичном кубе АВСDA1В1С1D1 найдите
- 5. 4. В единичном кубе АВСDA1В1С1D1 найдите
- 6. Задачи на нахождение расстояния между двумя скрещивающимися
- 7. 5. В единичном кубе АВСDA1В1С1D1 найдите
- 8. 6. В единичном кубе АВСDA1В1С1D1 найдите
- 9. 7. В единичном кубе АВСDA1В1С1D1 найдите
- 10. Предлагаемая методика тренировочных задач реализована в пособиях:Смирнова
Слайд 1Задачи на нахождение расстояния от точки до прямой
Расстоянием от точки до
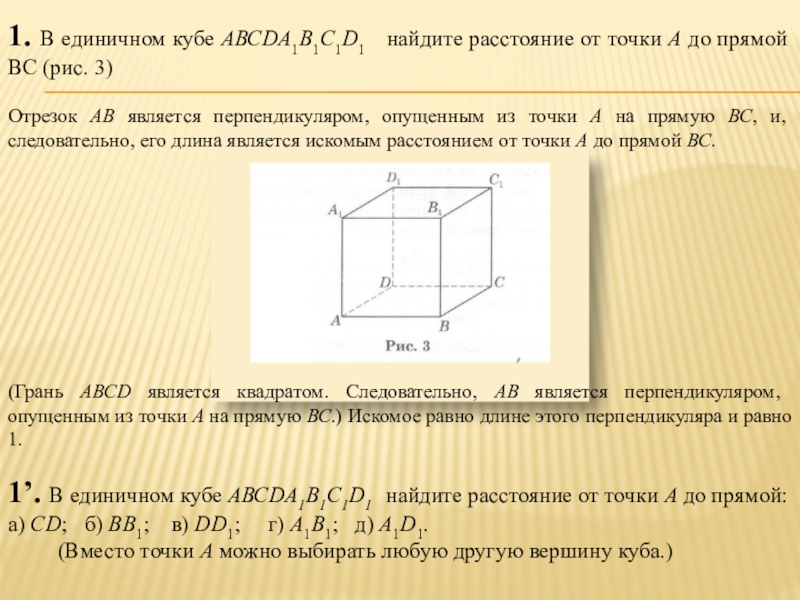
Слайд 21. В единичном кубе АВСDA1В1С1D1 найдите расстояние от точки А
Отрезок АВ является перпендикуляром, опущенным из точки А на прямую ВС, и, следовательно, его длина является искомым расстоянием от точки А до прямой ВС.
(Грань АВСD является квадратом. Следовательно, АВ является перпендикуляром, опущенным из точки А на прямую ВС.) Искомое равно длине этого перпендикуляра и равно 1.
1’. В единичном кубе АВСDA1В1С1D1 найдите расстояние от точки А до прямой: а) CD; б) ВВ1; в) DD1; г) А1В1; д) A1D1.
(Вместо точки А можно выбирать любую другую вершину куба.)
Слайд 32’. В единичном кубе АВСDA1В1С1D1 найдите расстояние от точки А
Так же как и в предыдущих задачах, вместо точки А можно брать любую другую вершину куба.
2. В единичном кубе АВСDA1В1С1D1 найдите расстояние от точки А до прямой ВС1 (рис. 4)
Для доказательства перпендикулярности прямых АВ и ВС1 можно воспользоваться тем, что прямая АВ перпендикулярна плоскости ВСС1 и, значит, перпендикулярна любой прямой, лежащей на этой плоскости. Искомое расстояние равно длине отрезка АВ и равно 1.
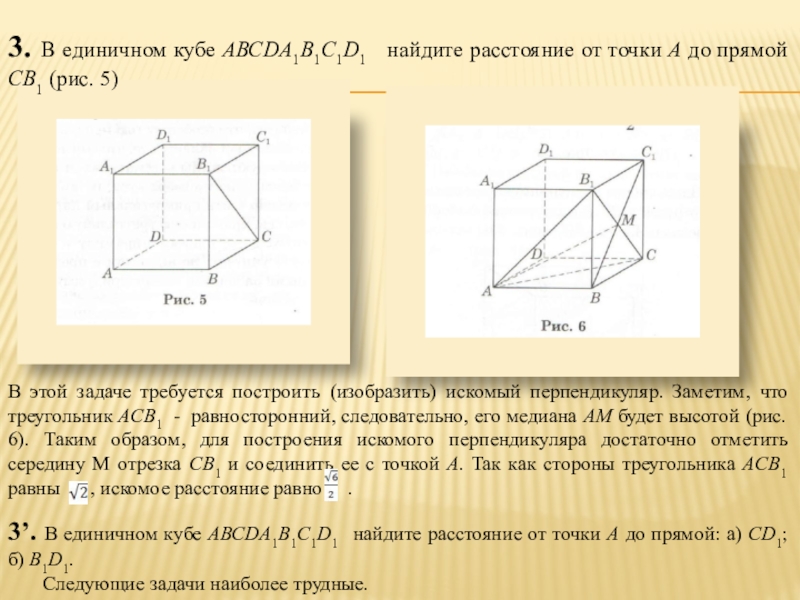
Слайд 43. В единичном кубе АВСDA1В1С1D1 найдите расстояние от точки А
В этой задаче требуется построить (изобразить) искомый перпендикуляр. Заметим, что треугольник АСВ1 - равносторонний, следовательно, его медиана АМ будет высотой (рис. 6). Таким образом, для построения искомого перпендикуляра достаточно отметить середину М отрезка СВ1 и соединить ее с точкой А. Так как стороны треугольника АСВ1 равны , искомое расстояние равно .
3’. В единичном кубе АВСDA1В1С1D1 найдите расстояние от точки А до прямой: а) СD1; б) В1D1.
Следующие задачи наиболее трудные.
Слайд 54. В единичном кубе АВСDA1В1С1D1 найдите расстояние от точки А
Для нахождения искомого перпендикуляра рассмотрим треугольник АВD1 (рис. 8). Он является прямоугольным (угол А – прямой) с катетами АВ = 1, AD1 = и гипотенузой BD1 = . Найдем его высоту AN. Для этого можно использовать или преобразование подобия, или тригонометрические функции, или площадь треугольника. Искомое расстояние равно .
4’. В единичном кубе АВСDA1В1С1D1 найдите расстояние от точки А до прямой: а) DВ1; б) СА1.
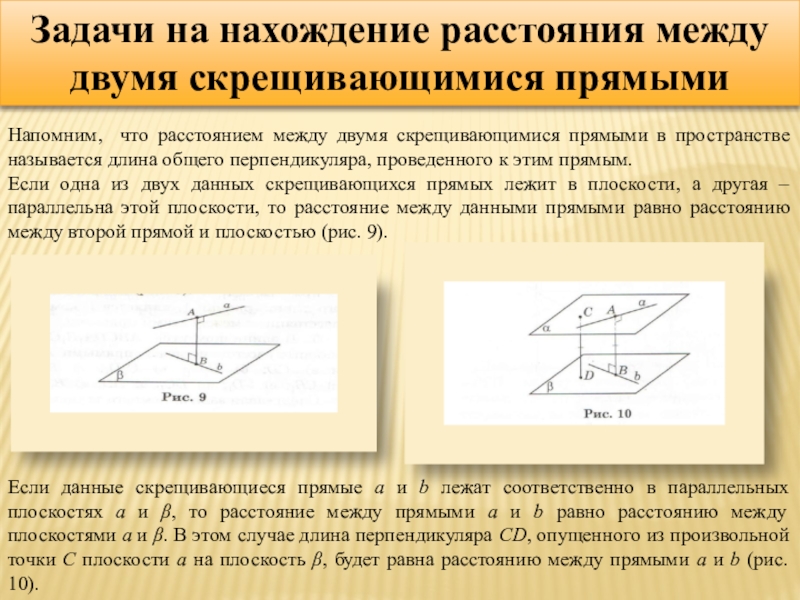
Слайд 6Задачи на нахождение расстояния между двумя скрещивающимися прямыми
Напомним, что расстоянием между
Если одна из двух данных скрещивающихся прямых лежит в плоскости, а другая – параллельна этой плоскости, то расстояние между данными прямыми равно расстоянию между второй прямой и плоскостью (рис. 9).
Если данные скрещивающиеся прямые a и b лежат соответственно в параллельных плоскостях ɑ и β, то расстояние между прямыми a и b равно расстоянию между плоскостями ɑ и β. В этом случае длина перпендикуляра CD, опущенного из произвольной точки C плоскости ɑ на плоскость β, будет равна расстоянию между прямыми a и b (рис. 10).
Слайд 75. В единичном кубе АВСDA1В1С1D1 найдите расстояние между прямыми АА1
Отрезок АВ является общим перпендикуляром к скрещивающимся прямым АА1 и ВС и, следовательно, его длина, равная 1, является искомым расстоянием между этими прямыми.
5’. В единичном кубе АВСDA1В1С1D1 найдите расстояние от точки АА1 до прямой: а) СD; б) В1С1; в) C1D1; г) BC1; д) CB1; е) CD1; ж) DC1; з) BD; и)B1D1.
Следующая задача немного труднее.
Слайд 86. В единичном кубе АВСDA1В1С1D1 найдите расстояние между прямыми АА1
Здесь общим перпендикуляром является отрезок ЕF, соединяющий середины отрезков АА1 и BD1 (рис. 13).
Действительно, пусть О – центр грани ABCD (рис.14). В четырехугольнике AOFE стороны АЕ и OF равны и параллельны. Значит, этот четырехугольник – параллелограмм, следовательно, стороны EF и AO равны и параллельны.
Прямая АА1 перпендикулярна АО, так как она перпендикулярна плоскости АВС. Прямая BD1 перпендикулярна АО по теореме о трех перпендикулярах. Следовательно, и прямая EF перпендикулярна АА1 и ВД1. ЕF является искомым общим перпендикуляром, длина которого равна .
6’. В единичном кубе АВСDA1В1С1D1 найдите расстояние между прямыми: а) АА1 и DB1 ; б) АВ и СА1; в) ВС и АС1; г) СD и BD1; д) AD и BD1.
Наиболее трудной из этой серии является следующая задача.
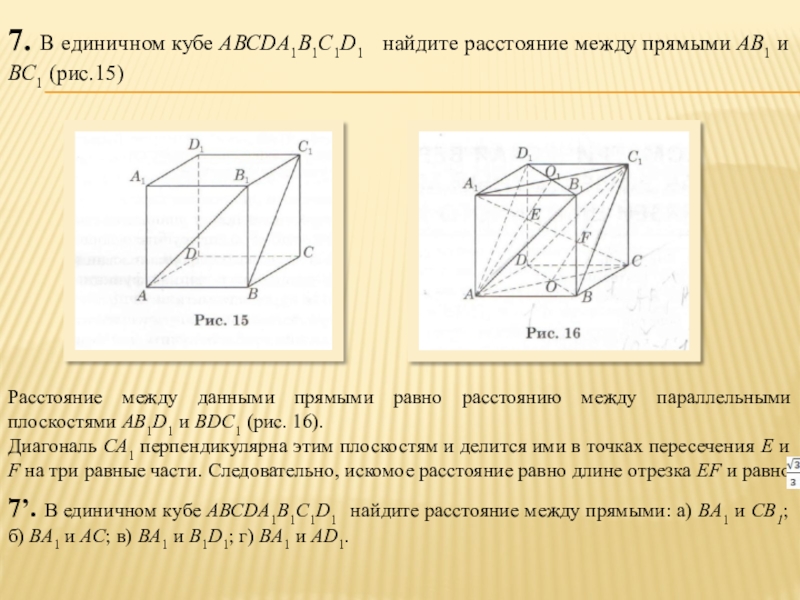
Слайд 97. В единичном кубе АВСDA1В1С1D1 найдите расстояние между прямыми АВ1
Расстояние между данными прямыми равно расстоянию между параллельными плоскостями АВ1D1 и BDC1 (рис. 16).
Диагональ СА1 перпендикулярна этим плоскостям и делится ими в точках пересечения E и F на три равные части. Следовательно, искомое расстояние равно длине отрезка EF и равно .
7’. В единичном кубе АВСDA1В1С1D1 найдите расстояние между прямыми: а) ВА1 и СB1; б) ВА1 и AС; в) ВА1 и B1D1; г) BA1 и AD1.
Слайд 10Предлагаемая методика тренировочных задач реализована в пособиях:
Смирнова И.М., Смирнов В.А. Геометрия.
Смирнова И.М., Смирнов В.А. Геометрия. Расстояния и углы в пространстве. – М. : Экзамен, 2009. – (ЕГЭ 100 баллов).
Смирнова И.М., Смирнов В.А. Геометрия.. Объемы и площади поверхностей пространственных фигур. – М. : Экзамен, 2009. - (ЕГЭ 100 баллов).
Смирнов В.А. Геометрия. Стереометрия : пособие для подготовки к ЕГЭ / под ред. И.В. Ященко и А.В. Семенова. – М.:МЦНМО, 2009.
Презентация выполнена по материалам статьи
«Как научить школьников решать задачи по геометрии?»
И.М.Смирновой, В.А.Смирнова. Математика в школе. №8, 2010г.