- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Многогранники (10 класс)
Содержание
- 1. Презентация по математике на тему Многогранники (10 класс)
- 2. Вопрос о целесообразности использования элементов истории математики
- 3. Принцип историзма в изучении математики: - осуществляет
- 4. Анализ программ, учебников школьной математики,
- 5. Многогранники. Уроки стереометрии в 10 классе ИКК
- 6. Правильные многогранники с древних времён привлекали к
- 7. Ко временам Платона в античной философии уже
- 8. Между основными стихиями помещаются две средние –
- 9. Атомам воды – форму икосаэдра, так как
- 10. Атома воздуха – форму октаэдра, ибо воздух
- 11. Атомам огня – форму тетраэдра как наиболее
- 12. Урок 2. Решение задач на нахождение элементов правильных многогранников. ИКК: «Многогранники в архитектуре».
- 13. Великая пирамида в Гизе. Эта грандиозная Египетская
- 14. Александрийский маяк. В третьем веке до н.э.
- 15. Урок 3-4. Вычисление площадей поверхностей правильных многогранников. ИКК: « Многогранники в искусстве»
- 16. Леонардо да Винчи (1452-1519) увлекался теорией многогранников
- 17. Модели многогранников и гравюры многогранников выполнены голландским художником-графиком М.К.Эшером.
- 18. Перед вами изображение картины художника Сальвадора Дали «Тайная Вечеря».
- 19. Это огромное полотно, в котором художник решил
- 20. Ещё одним знаменитым художником эпохи Возрождения увлекавшимся
- 21. Уроки 5-6. Практическая работа по построению разверток многогранников ИКК: «Многогранники в природе».
- 22. Чем хорош для пчел правильный шестиугольникСоты в разрезе плоскостью, перпендикулярной боковому ребру, и развертка
- 23. Уроки 7-8. Зачетные уроки по теме «Правильные многогранники» ИКК: «Многогранники в науках».
- 24. Кристаллы белого фосфора образованы молекулами Р4. Такая
- 25. молекула ДНК составлена из взаимоотношений двойственности додекаэдров и икосаэдров.
- 26. Алмазы обычно имеют октаэдр в качестве формы
Вопрос о целесообразности использования элементов истории математики в изучении предмета не является принципиально новым. На его значимость указывали многие известные математики: в частности Джон Валлис (17в.), Клод Клеро (18в.), Мишель Шаль (19в.), Анри Пуанкаре (20в.).
Слайд 1Историко-культурный компонент как один из факторов гуманитаризации математического образования учащихся
Слайд 2Вопрос о целесообразности использования элементов истории математики в изучении предмета
не является принципиально новым. На его значимость указывали многие известные математики: в частности Джон Валлис (17в.), Клод Клеро (18в.), Мишель Шаль (19в.), Анри Пуанкаре (20в.). Российские учёные-математики также придавали серьёзное внимание включению исторической компоненты в преподавании математики. На это указывается в статьях Бобынина, Брадиса, Маркушевича, Юшкевича, Виленкина и других.
Слайд 3Принцип историзма в изучении математики:
- осуществляет следующие функции: мировоззренческая, гносеологическая
(познавательная), прогностическая (от prognostihos-прогнозировать), общекультурная, информационная, креативная, воспитательная, развивающая, эстетическая.
- реализует диалектику математического знания ( прошлое, настоящее, будущее науки)
- позволяет осмыслить целостность, обобщенность и системность математического знания.
- реализует диалектику математического знания ( прошлое, настоящее, будущее науки)
- позволяет осмыслить целостность, обобщенность и системность математического знания.
Слайд 4 Анализ программ, учебников школьной математики, на наш взгляд, позволяет
выделить следующие линии историко- культурного компонента:
мировоззренческую,
персоналитическую (биографии, имена ученых, их вклад в развитие математической науки)
линию расширения понятия числа, уравнений и функций.
мировоззренческую,
персоналитическую (биографии, имена ученых, их вклад в развитие математической науки)
линию расширения понятия числа, уравнений и функций.
Слайд 5Многогранники.
Уроки стереометрии в 10 классе
ИКК на уроках математики.
Урок1.
Многогранники.
ИКК : «Правильные
многогранники в философской картине мира Платона»
Слайд 6Правильные многогранники с древних времён привлекали к себе внимание учёных, архитекторов,
художников и т.д. Их поражала красота, совершенство, гармония этих многогранников.
Пифагорейцы считали эти многогранники божественными и использовали их в своих философских сочинениях о существе мира.
Подробно описал свойства правильных многогранников древнегреческий учёный Платон. Именно поэтому правильные многогранники называются также телами Платона.
Пифагорейцы считали эти многогранники божественными и использовали их в своих философских сочинениях о существе мира.
Подробно описал свойства правильных многогранников древнегреческий учёный Платон. Именно поэтому правильные многогранники называются также телами Платона.
Слайд 7Ко временам Платона в античной философии уже созрела концепция четырёх элементов
(стихий) – первооснов материального мира:
огня, воздуха, воды и земли.
огня, воздуха, воды и земли.
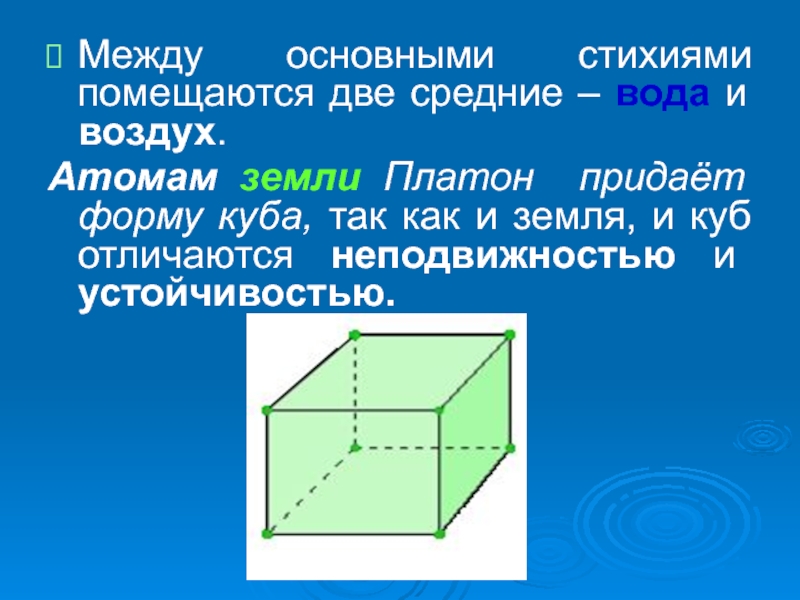
Слайд 8Между основными стихиями помещаются две средние – вода и воздух.
Атомам
земли Платон придаёт форму куба, так как и земля, и куб отличаются неподвижностью и устойчивостью.
Слайд 9Атомам воды – форму икосаэдра, так как вода отличается текучестью, а
из всех правильных тел
икосаэдр – наиболее
«катящийся».
икосаэдр – наиболее
«катящийся».
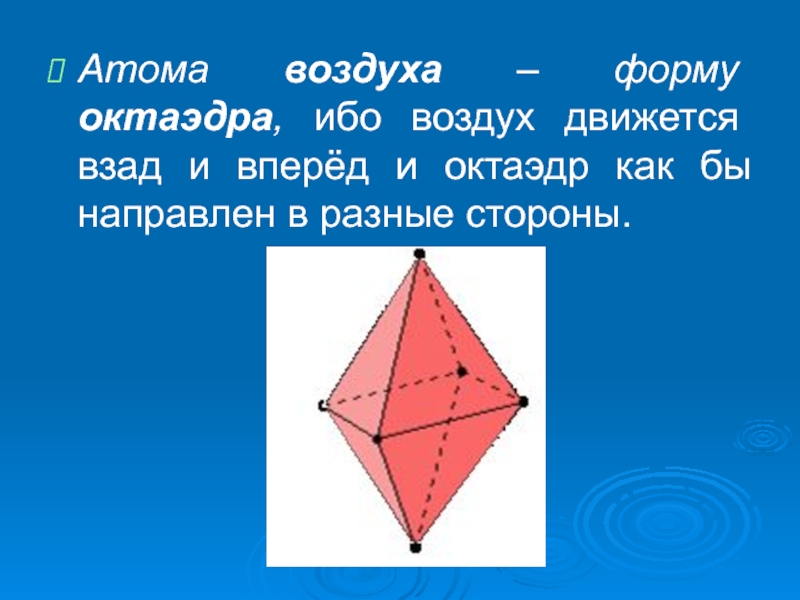
Слайд 10Атома воздуха – форму октаэдра, ибо воздух движется взад и вперёд
и октаэдр как бы направлен в разные стороны.
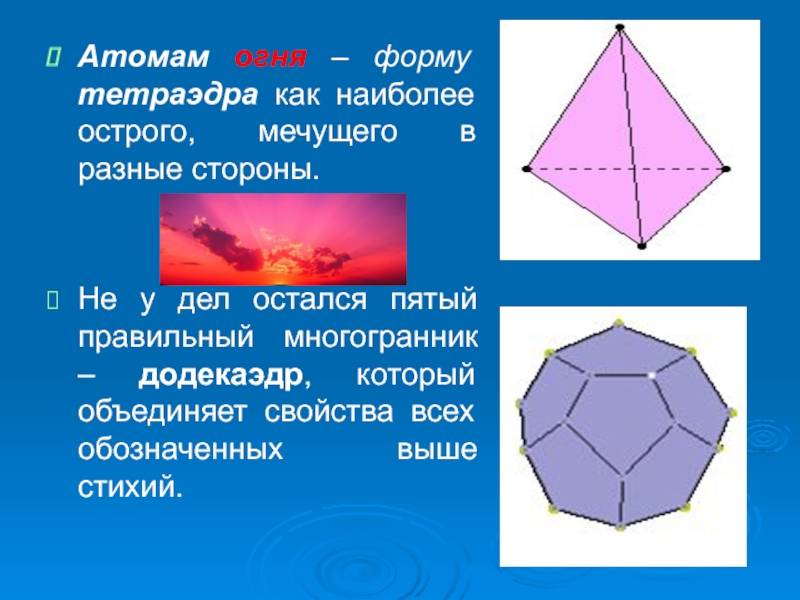
Слайд 11Атомам огня – форму тетраэдра как наиболее острого, мечущего в разные
стороны.
Не у дел остался пятый правильный многогранник – додекаэдр, который объединяет свойства всех обозначенных выше стихий.
Не у дел остался пятый правильный многогранник – додекаэдр, который объединяет свойства всех обозначенных выше стихий.
Слайд 12Урок 2.
Решение задач на нахождение элементов правильных многогранников.
ИКК: «Многогранники в архитектуре».
Слайд 13
Великая пирамида в Гизе. Эта грандиозная Египетская пирамида является древнейшим из
семи чудес, сохранившемся до наших дней. И удержала она этот рекорд, по всей видимости, почти 4000 лет.
Слайд 14Александрийский маяк. В третьем веке до н.э. был построен маяк, чтобы
корабли могли благополучно миновать рифы на пути в Александрийскую бухту. Ночью им помогло в этом отражение языков пламени, а днём - столб дыма. Это был первый в мире маяк, и простоял он 1500 лет.
Слайд 15Урок 3-4. Вычисление площадей поверхностей правильных многогранников. ИКК: « Многогранники в искусстве»
Слайд 16Леонардо да Винчи (1452-1519) увлекался теорией многогранников и часто изображал их
на своих полотнах. Он проиллюстрировал правильными и полуправильными многогранниками книгу Монаха Луки Пачоли «О божественной пропорции».
Наиболее интересной из работ голладского художника-графика М.К.Эшера является гравюра «Звезды», на которой можно увидеть тела, полученные объединением тетраэдров, кубов и октаэдров.
Наиболее интересной из работ голладского художника-графика М.К.Эшера является гравюра «Звезды», на которой можно увидеть тела, полученные объединением тетраэдров, кубов и октаэдров.
Слайд 17Модели многогранников и гравюры многогранников выполнены голландским
художником-графиком М.К.Эшером.
Слайд 19Это огромное полотно, в котором художник решил посоревноваться с Леонардо да
Винчи. Обратите внимание, что изображено на переднем плане картины? Христос со своими учениками изображён на фоне огромного прозрачного додекаэдра. Это объясняется тем, что (как говорилось ранее) по учению Платона атомам Вселенной придаётся форма додекаэдра.
Слайд 20Ещё одним знаменитым художником эпохи Возрождения увлекавшимся геометрией, был Альбрехт Дюрер.
В своей гравюре «Меланхолия» он дал перспективное изображение додекаэдра.
Слайд 21Уроки 5-6.
Практическая работа по построению разверток многогранников
ИКК: «Многогранники в природе».
Слайд 22Чем хорош для пчел правильный шестиугольник
Соты в разрезе плоскостью, перпендикулярной боковому
ребру, и развертка
Слайд 24Кристаллы белого фосфора образованы молекулами Р4.
Такая молекула имеет вид тетраэдра.
Куб
передаёт форму кристаллов поваренной соли (NaCl).
Форму куба имеют кристаллической решётки многих металлов (Li, Na, Cr, Pb, Al, Au и другие)
Форму куба имеют кристаллической решётки многих металлов (Li, Na, Cr, Pb, Al, Au и другие)
Слайд 26Алмазы обычно имеют октаэдр в качестве формы огранки.
Алмаз (от
греч. adamas – несокрушимый) – бесцветный или окрашенный кристалл с сильным блеском в виде октаэдра.
Кристаллы алмаза представляют собой гигантские полимерные молекулы и обычно имеют форму огранки октаэдра, ромбододекаэдра, реже – куба или тетраэдра.
Кристаллы алмаза представляют собой гигантские полимерные молекулы и обычно имеют форму огранки октаэдра, ромбододекаэдра, реже – куба или тетраэдра.