- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Многогранники 10 класс
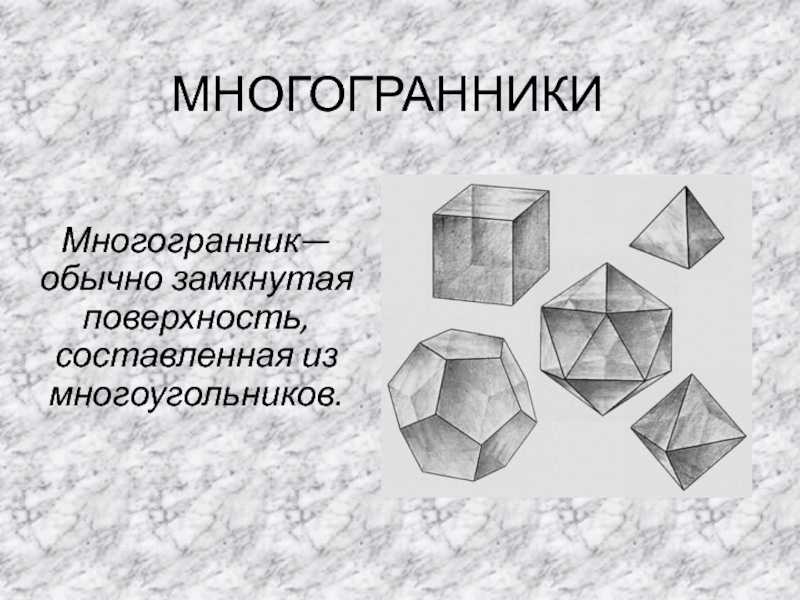
Содержание
- 1. Презентация по математике на тему Многогранники 10 класс
- 2. ИСТОРИЯИстория правильных многогранников уходит в глубокую древность.
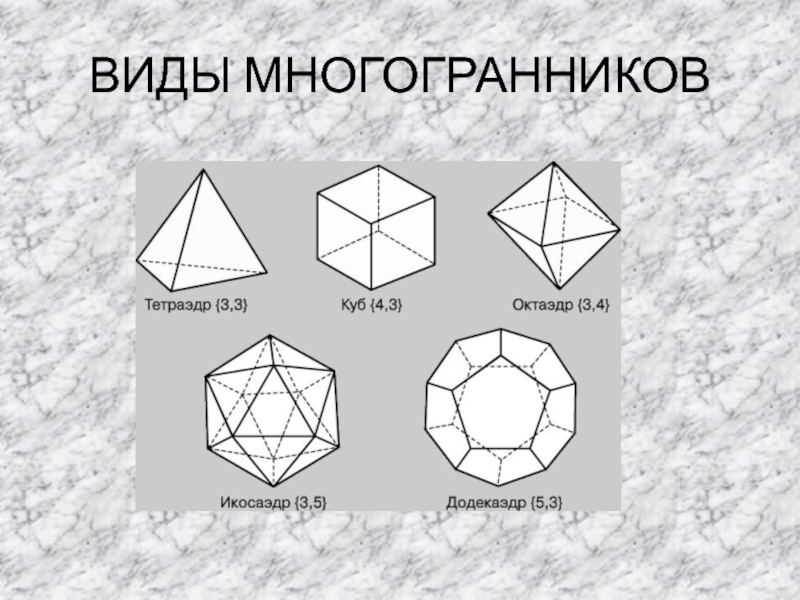
- 3. ВИДЫ МНОГОГРАННИКОВ
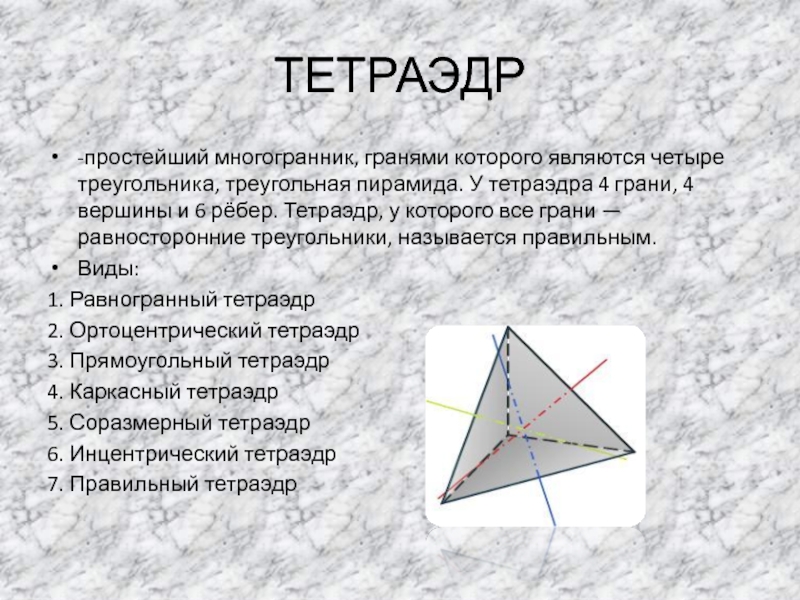
- 4. ТЕТРАЭДР-простейший многогранник, гранями которого являются четыре треугольника,
- 5. КУБ — правильный многогранник, каждая грань которого
- 6. ОТКАЭДР— многогранник с восемью гранями. Правильный октаэдр
- 7. ИКОСАЭДРправильный икосаэдр - выпуклый многогранник, двадцатигранник, одно
- 8. ДОДЕКАЭДРодин из пяти возможных правильных многогранников. Додекаэдр
- 9. ПЕНТАГОНДОДЕКАЭРДобъёмная фигура с двенадцатью гранями в форме
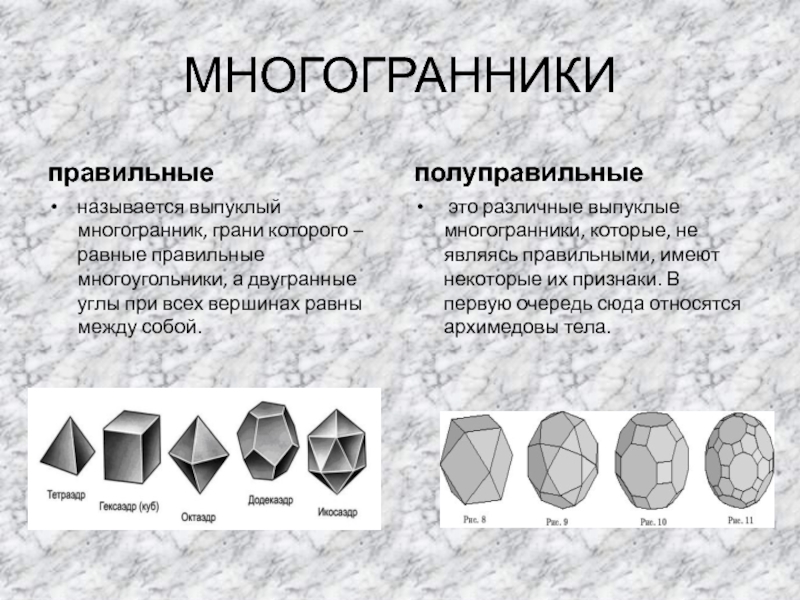
- 10. МНОГОГРАННИКИправильныеназывается выпуклый многогранник, грани которого – равные
- 11. В каждом правильном многограннике сумма числа граней
- 12. ПЛАТОН
- 13. МНОГОГРАННИКИ В НАШЕЙ ЖИЗНИ1. в природе2. в
ИСТОРИЯИстория правильных многогранников уходит в глубокую древность. Начиная с 7 века до нашей эры в Древней Греции создаются философские школы. Большое значение в этих школах приобретают рассуждения, с помощью которых удалось получать новые геометрические свойства. Одной
Слайд 2ИСТОРИЯ
История правильных многогранников уходит в глубокую древность. Начиная с 7 века
до нашей эры в Древней Греции создаются философские школы. Большое значение в этих школах приобретают рассуждения, с помощью которых удалось получать новые геометрические свойства. Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Отличительным знаком пифагорейцев была пентаграмма, на языке математики- это правильный невыпуклый или звездчатый пятиугольник.
Пифагорейцы полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды. Существование пяти правильных многогранников они относили к строению материи и Вселенной. Согласно этому мнению, атомы основных элементов должны иметь форму различных тел:
Пифагорейцы полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды. Существование пяти правильных многогранников они относили к строению материи и Вселенной. Согласно этому мнению, атомы основных элементов должны иметь форму различных тел:
Вселенная - додекаэдр
Земля - куб
Огонь - тетраэдр
Вода - икосаэдр
Воздух - октаэдр
Слайд 4ТЕТРАЭДР
-простейший многогранник, гранями которого являются четыре треугольника, треугольная пирамида. У тетраэдра
4 грани, 4 вершины и 6 рёбер. Тетраэдр, у которого все грани — равносторонние треугольники, называется правильным.
Виды:
1. Равногранный тетраэдр
2. Ортоцентрический тетраэдр
3. Прямоугольный тетраэдр
4. Каркасный тетраэдр
5. Соразмерный тетраэдр
6. Инцентрический тетраэдр
7. Правильный тетраэдр
Виды:
1. Равногранный тетраэдр
2. Ортоцентрический тетраэдр
3. Прямоугольный тетраэдр
4. Каркасный тетраэдр
5. Соразмерный тетраэдр
6. Инцентрический тетраэдр
7. Правильный тетраэдр
Слайд 5КУБ
— правильный многогранник, каждая грань которого представляет собой квадрат. Каждая
его вершина является вершиной трех квадратов. Частный случай параллелепипеда и призмы. У куба: вершин 8, рёбер 12, граней 6, граней при вершине 3.
Слайд 6ОТКАЭДР
— многогранник с восемью гранями. Правильный октаэдр является одним из пяти
выпуклых правильных многогранников, так называемых платоновых тел; грани правильного октаэдра — восемь равносторонних треугольников. Правильный октаэдр имеет 8 треугольных граней, 12 рёбер, 6 вершин, в каждой его вершине сходятся 4 ребра.
Слайд 7ИКОСАЭДР
правильный икосаэдр - выпуклый многогранник, двадцатигранник, одно из Платоновых тел. Каждая
из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин — 12. Икосаэдр имеет 59 звёздчатых форм.
усечённый икосаэдр - многогранник, состоящий из 12 правильных пятиугольников и 20 правильных шестиугольников. Имеет икосаэдрический тип симметрии. По сути классический футбольный мяч имеет форму не шара, а усечённого икосаэдра с выпуклыми (сферическими) гранями.
усечённый икосаэдр - многогранник, состоящий из 12 правильных пятиугольников и 20 правильных шестиугольников. Имеет икосаэдрический тип симметрии. По сути классический футбольный мяч имеет форму не шара, а усечённого икосаэдра с выпуклыми (сферическими) гранями.
Слайд 8ДОДЕКАЭДР
один из пяти возможных правильных многогранников. Додекаэдр составлен из двенадцати правильных
пятиугольников, являющихся его гранями. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Таким образом, додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра).
Слайд 9ПЕНТАГОНДОДЕКАЭРД
объёмная фигура с двенадцатью гранями в форме неправильных пятиугольников. Относится к
додекаэдрам. Визуально он похож на платоновский додекаэдр, но имеет не икосаэдрическую, а тетраэдрическую симметрию. Грани пентагондодекаэдра — неправильные пятиугольники, симметричные относительно плоскости, проходящей через центр фигуры. Граней 12, рёбер 30, вершин 20, граней при вершине 3.
Слайд 10МНОГОГРАННИКИ
правильные
называется выпуклый многогранник, грани которого – равные правильные многоугольники, а двугранные
углы при всех вершинах равны между собой.
полуправильные
это различные выпуклые многогранники, которые, не являясь правильными, имеют некоторые их признаки. В первую очередь сюда относятся архимедовы тела.
Слайд 11В каждом правильном многограннике сумма числа граней и вершин равна числу
ребер, увеличенному на 2.
Г+В=Р+2
Слайд 13МНОГОГРАННИКИ В НАШЕЙ ЖИЗНИ
1. в природе
2. в живописи
3. в архитектуре
4.
в изготовление мебели
5. в изготовлении ювелирных изделий
6. в оригами
5. в изготовлении ювелирных изделий
6. в оригами