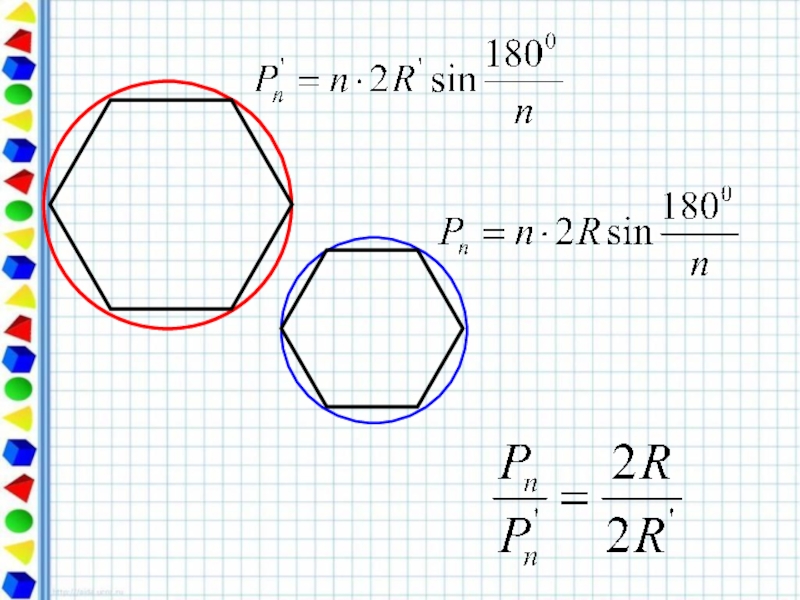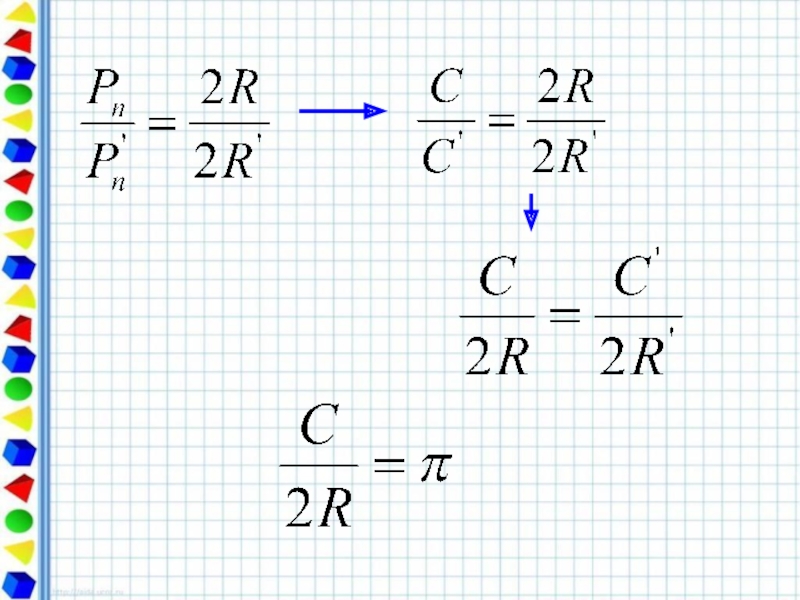- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Длина окружности
Содержание
- 1. Презентация по математике на тему Длина окружности
- 2. Дайте названия линиям и точкам Какой формулой
- 3. Длину отрезка можно измерить
- 4. Представим. Что мы разрезаем окружность и «распрямляем»
- 5. Длина окружности обозначается буквой C.
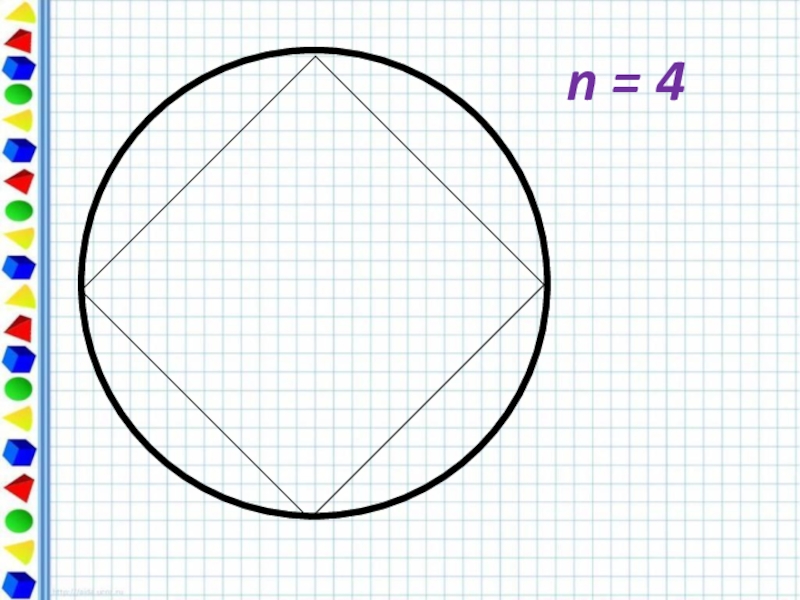
- 6. n = 4
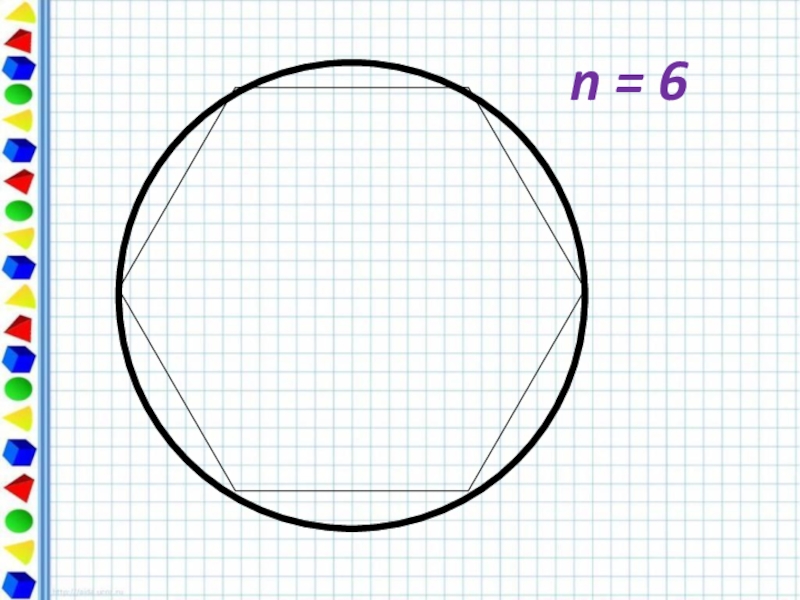
- 7. n = 6
- 8. n = 8
- 9. Слайд 9
- 10. Периметр любого вписанного в окружность многоугольника
- 11. Слайд 11
- 12. Слайд 12
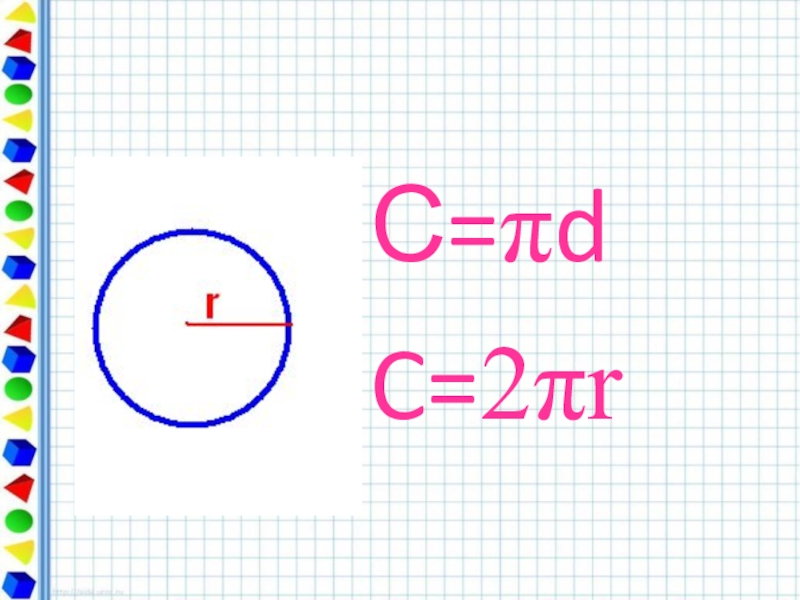
- 13. С=πdC=2πr
- 14. O1Свойство длины окружности.Отношение длины окружности к её
- 15. Число Π
- 16. ≈3,14159265358 9793238462643…π≈3,14=227
- 17. Обозначение числа происходит от первой буквы греческого
- 18. А есть и стихотворения, например: Чтобы нам
- 19. Из древнеегипетских и вавилонских источников известно, что
- 20. Вычислением числа занимались в более поздние
- 21. Мировой рекорд по запоминанию знаков числа П
- 22. 510 знаков после запятой: π ≈ 3,141
- 23. Сто миллионов знаков после запятой3,1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811745028410270193852110555964462294895493038196442881097566593344612847564823378678316527120190914564856692346034861045432648213393607260249141273724587006606315588174881520920962829254091715364367892590360011330530548820466521384146951941511609433057270365759591953092186117381932611793105118548074462379962749567351885752724891227938183011949129833673362440656643086021394946395224731907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235420199561121290219608640344181598136297747713099605187072113499999983729780499510597317328160963185950244594553469083026425223082533446850352619311881710100031378387528865875332083814206171776691473035982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989380952572010654858632788659361533818279682303019520353018529689957736225994138912497217752834791315155748572424541506959508295331168617278558890750983817546374649393192550604009277016711390098488240128583616035637076601047101819429555961989467678374494482553797747268471040475346462080466842590694912933136770289891521047521620569660240580381501935112533824300355876402474964732639141992726042699227967823547816360093417216412199245863150302861829745557067498385054945885869269956909272107975093029553211653449872027559602364806654991198818347977535663698074265425278625518184175746728909777727938000816470600161452491921732172147723501414419735685481613611573525521334757418494684385233239073941433345477624168625189835694855620992192221842725502542568876717904946016534668049886272327917860857843838279679766814541009538837863609506800642251252051173929848960841284886269456042419652850222106611863067442786220391949450471237137869609563643719172874677646575739624138908658326459958133904780275900994657640789512694683983525957098258226205224894077267194782684826014769909026401363944374553050682034962524517493996514314298091906592509372216964615157098583874105978859597729754989301617539284681382686838689427741559918559252459539594310499725246808459872736446958486538367362226260991246080512438843904512441365497627807977156914359977001296160894416948685558484063534220722258284886481584560285060168427394522674676788952521385225499546667278239864565961163548862305774564980355936345681743241125150760694794510965960940252288797108931456691368672287489405601015033086179286809208747609178249385890097149096759852613655497818931297848216829989487226588048575640142704775551323796414515237462343645428584447952658678210511413547357395231134271661021359695362314429524849371871101457654035902799344037420073105785390621983874478084784896833214457138687519435064302184531910484810053706146806749192781911979399520614196634287544406437451237181921799983910159195618146751426912397489409071864942319615679452080951465502252316038819301420937621378559566389377870830390697920773467221825625996615014215030680384477345492026054146659252014974428507325186660021324340881907104863317346496514539057962685610055081066587969981635747363840525714591028970641401109712062804390397595156771577004203378699360072305587631763594218731251471205329281918261861258673215791984148488291644706095752706957220917567116722910981690915280173506712748583222871835209353965725121083579151369882091444210067510334671103141267111369908658516398315019701651511685171437657618351556508849099898599823873455283316355076479185358932261854896321329330898570642046752590709154814165498594616371802709819943099244889575712828905923233260972997120844335732654893823911932597463667305836041428138830320382490375898524374417029132765618093773444030707469211201913020330380197621101100449293215160842444859637669838952286847831235526582131449576857262433441893039686426243410773226978028073189154411010446823252716201052652272111660396
- 24. Теперь известно, что число иррациональное, может
- 25. Существует даже праздник числа П! Неофициальный праздник
- 26. В Сиэтле (США) существует памятник числу П, который находится на ступенях перед зданием Музея искусств
- 27. Задачи по теме «Длина окружности»Порешаем!!!
- 28. Теоретические сведенияОО – центр окружностиr- радиус окружностиd- диаметр окружностиC – длина окружности
- 29. Задача:1) вычислить длину окружности, если ее диаметр
- 30. Решение:1)D=6 см С=
- 31. Задача: Длина окружности цирковой арены
- 32. Решение:С = П DС=41 м 41 =
- 33. Диаметр d= 5мО?Длина окружности – СЦветочная клумба
- 34. С = 3,14•5=15,7 (м) Ответ: длина
- 35. Ныне самым старым деревом является гигантский
- 36. Решите задачуУ лукоморья дуб зелёный;Златая цепь на
- 37. Решение 0,35 * 6 = 2,1 (км)
- 38. Отлитый в 1735
- 39. Решите задачуПришкольная площадка имеет форму квадрата периметром
- 40. Решите задачуНаконец и в путь обратныйСо своею
- 41. Решите задачуНа побережье Средиземного моря растет интересное
- 42. Задача (О Тунгусском
- 43. Древнегреческий математик Архимед установил, что
- 44. Верхушка головы -
- 45. Обычно отвечают, что промежуток будет тоньше волоса.
- 46. Найти длину окружности описанной около правильного треугольника
- 47. R
- 48. Найти длину окружности описанной около равнобедренного треугольника
- 49. Дана равнобедренная трапеция со сторонами 2a, a,
- 50. Так как шестиугольник правильный, то радиус описанной
- 51. Архимед в III в. до н.э. обосновал в своей
- 52. В первой половине XV в. обсерватории Улугбека,
- 53. Интересные факты Отношение длины основания Великой
- 54. Интересные факты Лидером по тупым законам
- 55. ДОМАШНЕЕ ЗАДАНИЕ
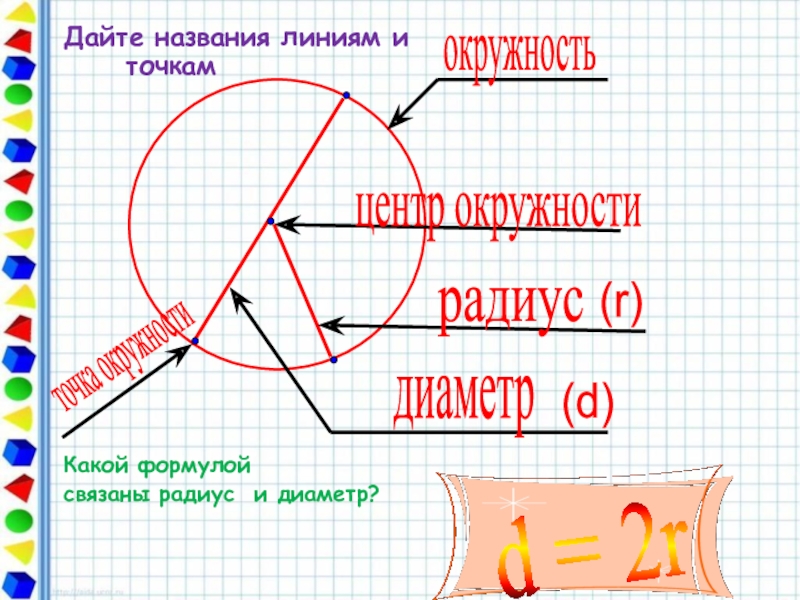
Слайд 2Дайте названия линиям и точкам
Какой формулой
связаны радиус и диаметр?
???
окружность
???
центр окружности
???
радиус
???
диаметр
(r)
(d)
???
d = 2r
???
точка окружности
Слайд 3
Длину отрезка можно измерить с помощью линейки, длину
А как вы думаете: каким
образом измерить длину
окружности без этого
прибора?
рис. 95
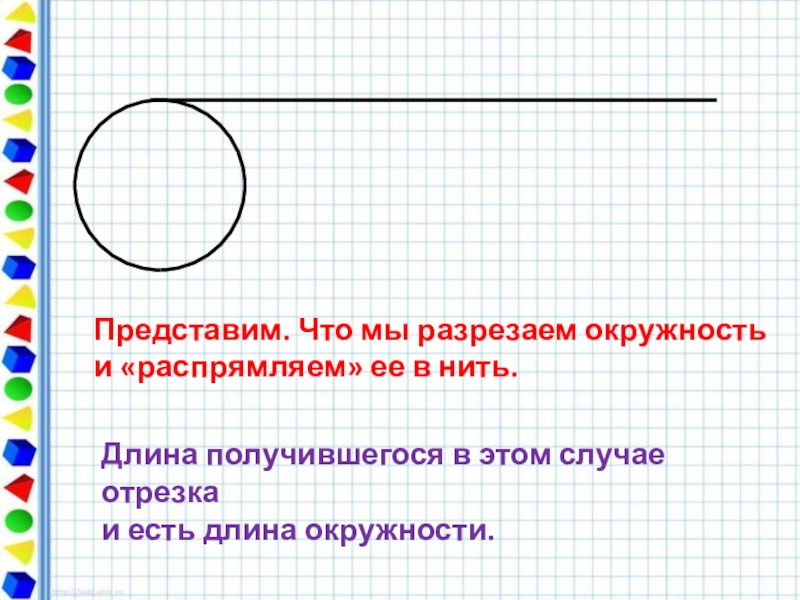
Слайд 4Представим. Что мы разрезаем окружность и «распрямляем» ее в нить.
Длина получившегося
и есть длина окружности.
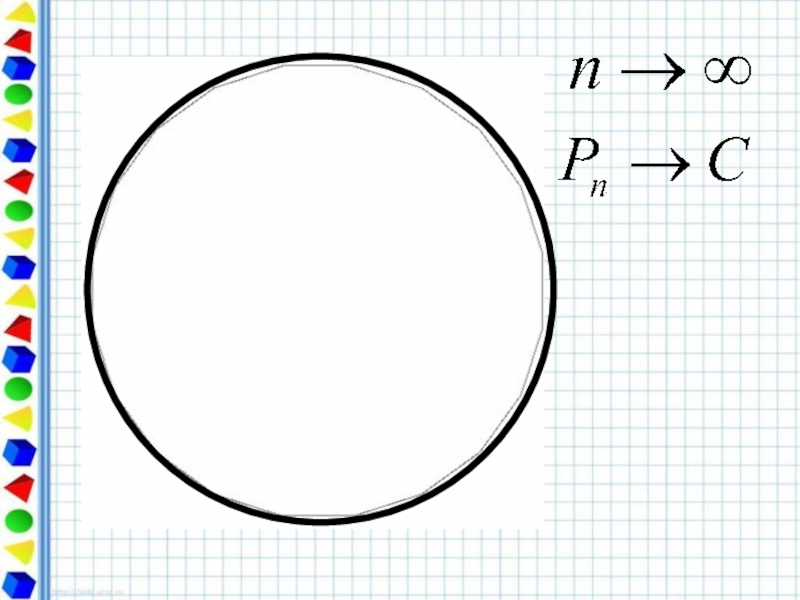
Слайд 10Периметр любого вписанного в окружность многоугольника является приближённым значением
При увеличении числа сторон правильный многоугольник всё ближе и ближе «прилегает» к окружности.
Длина окружности – это
предел, к которому стремится
периметр правильного
вписанного многоугольника при
неограниченном увеличении
числа его сторон.
Слайд 14O1
Свойство длины окружности.
Отношение длины окружности к её диаметру есть одно и
O2
Слайд 17Обозначение числа происходит от первой буквы греческого слова периферия, что означает
Чаще всего используется его значение, равное 3,14.
Более точное значение, равное 3,1416 легко запомнить по фразе: "Что я знаю о кругах". Здесь число букв в каждом слове дает соответствующую цифру в записи значения числа .
Обозначение буквой ввёл в употребление в 17 веке великий математик Леонард Эйлер.
Слайд 18А есть и стихотворения, например:
Чтобы нам не ошибаться,
девяносто два и шесть!
Есть и другие фразы для запоминания числа П:
«Это я знаю и помню прекрасно:
Пи многие знаки мне лишни, напрасны.
Доверимся знаньям громадным
Тех, пи кто сосчитал, цифр армаду»;
«Вот и знаю я число, именуемое Пи»;
3,14159265358979323846
3,141592
3,1415926
Слайд 19Из древнеегипетских и вавилонских источников известно, что потребности того времени вполне
В Древнем Египте считали равным 256/81=3,1604…
В истории математики известно, что первое вычисление на основе строгих теоретических рассуждений было выполнено выдающимся математиком древности Архимедом.
Архимед (ок.287-212 г.г. до н.э.) жил в г. Сиракузы на о. Сицилия. Погиб от рук римского воина. Перед гибелью Архимед сказал воину: «Не тронь мои круги!». В своем труде «Об измерении круга» он доказал, что находится между числами и , т.е. 3,1408 < <3,1429.
Идеи Архимеда почти на два тысячелетия опередили свое время. Значение числа , вычисленное им, многие годы удовлетворяло практическим расчетам людей.
Слайд 20Вычислением числа занимались в более поздние века многие знаменитые математики.
Французский
Голландский математик Лудольф Ван Цейлен в 1596 г. публикует результат своего десятилетнего труда – число , вычисленное с 32 знаками.
Леонард Эйлер (1707-1783) – ученый необычайной широты интересов и творческой продуктивности, автор свыше 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближенным вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки. Именно он в 1736 г ввел число для отношения длины окружности к длине ее диаметра.
Постепенно увеличивая точность значений, в течение XVIII-XX веков нашли его значение с огромной точностью до 808 десятичных знаков.
Слайд 21Мировой рекорд по запоминанию знаков числа П принадлежит японцу Акира Харагути
Ему понадобилось почти 16 часов, чтобы назвать всё число целиком (на запоминание ушло 10 лет).
Запомнить знаки П человечество пытается уже давно. Но как уложить в память бесконечность? Любимый вопрос мнемонистов-профессионалов. Разработано множество уникальных теорий и приёмов освоения огромного количества информации. Многие из них опробованы на П.
Мировой рекорд, установленный в прошлом столетии в Германии - 40 000 знаков. Российский рекорд значений числа П 1 декабря 2003 года в Челябинске установил Александр Беляев. За полтора часа с небольшими перерывами на школьной доске Александр написал 2500 цифр числа П.
Слайд 22
510 знаков после запятой:
π ≈ 3,141 592 653 589 793
Слайд 23Сто миллионов знаков после запятой
3,1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811745028410270193852110555964462294895493038196442881097566593344612847564823378678316527120190914564856692346034861045432648213393607260249141273724587006606315588174881520920962829254091715364367892590360011330530548820466521384146951941511609433057270365759591953092186117381932611793105118548074462379962749567351885752724891227938183011949129833673362440656643086021394946395224731907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235420199561121290219608640344181598136297747713099605187072113499999983729780499510597317328160963185950244594553469083026425223082533446850352619311881710100031378387528865875332083814206171776691473035982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989380952572010654858632788659361533818279682303019520353018529689957736225994138912497217752834791315155748572424541506959508295331168617278558890750983817546374649393192550604009277016711390098488240128583616035637076601047101819429555961989467678374494482553797747268471040475346462080466842590694912933136770289891521047521620569660240580381501935112533824300355876402474964732639141992726042699227967823547816360093417216412199245863150302861829745557067498385054945885869269956909272107975093029553211653449872027559602364806654991198818347977535663698074265425278625518184175746728909777727938000816470600161452491921732172147723501414419735685481613611573525521334757418494684385233239073941433345477624168625189835694855620992192221842725502542568876717904946016534668049886272327917860857843838279679766814541009538837863609506800642251252051173929848960841284886269456042419652850222106611863067442786220391949450471237137869609563643719172874677646575739624138908658326459958133904780275900994657640789512694683983525957098258226205224894077267194782684826014769909026401363944374553050682034962524517493996514314298091906592509372216964615157098583874105978859597729754989301617539284681382686838689427741559918559252459539594310499725246808459872736446958486538367362226260991246080512438843904512441365497627807977156914359977001296160894416948685558484063534220722258284886481584560285060168427394522674676788952521385225499546667278239864565961163548862305774564980355936345681743241125150760694794510965960940252288797108931456691368672287489405601015033086179286809208747609178249385890097149096759852613655497818931297848216829989487226588048575640142704775551323796414515237462343645428584447952658678210511413547357395231134271661021359695362314429524849371871101457654035902799344037420073105785390621983874478084784896833214457138687519435064302184531910484810053706146806749192781911979399520614196634287544406437451237181921799983910159195618146751426912397489409071864942319615679452080951465502252316038819301420937621378559566389377870830390697920773467221825625996615014215030680384477345492026054146659252014974428507325186660021324340881907104863317346496514539057962685610055081066587969981635747363840525714591028970641401109712062804390397595156771577004203378699360072305587631763594218731251471205329281918261861258673215791984148488291644706095752706957220917567116722910981690915280173506712748583222871835209353965725121083579151369882091444210067510334671103141267111369908658516398315019701651511685171437657618351556508849099898599823873455283316355076479185358932261854896321329330898570642046752590709154814165498594616371802709819943099244889575712828905923233260972997120844335732654893823911932597463667305836041428138830320382490375898524374417029132765618093773444030707469211201913020330380197621101100449293215160842444859637669838952286847831235526582131449576857262433441893039686426243410773226978028073189154411010446823252716201052652272111660396
Слайд 24Теперь известно, что число иррациональное, может быть представлено в виде
С помощью компьютера число вычислено с точностью до миллиона знаков, но это представляет скорее технический, чем научный интерес…
Слайд 25Существует даже праздник числа П! Неофициальный праздник «День числа Пи» отмечается
Ещё одной датой, связанной с числом П, является
22 июля, которое называется «Днём приближённого числа Пи» , так как в европейском формате дат этот день записывается как 22/7, а значение этой дроби является приближённым значением числа П.
Слайд 26В Сиэтле (США) существует памятник числу П, который находится на ступенях
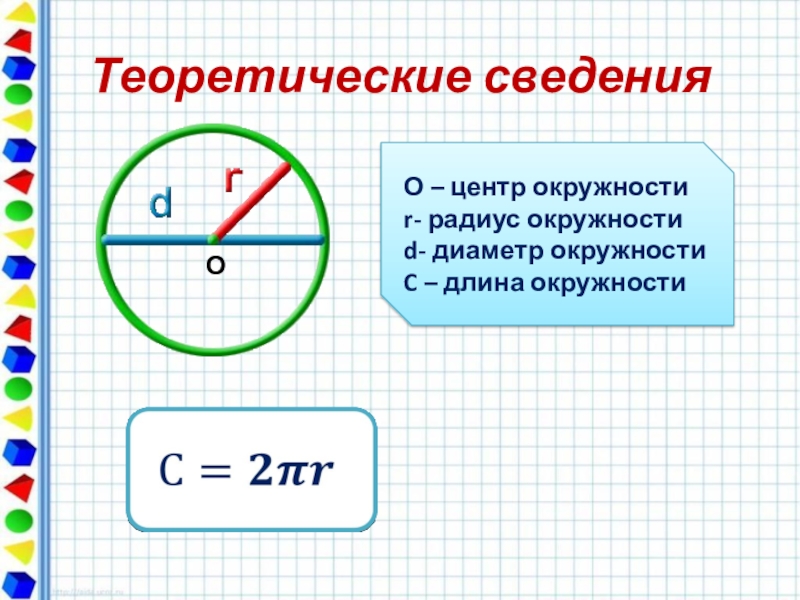
Слайд 28Теоретические сведения
О
О – центр окружности
r- радиус окружности
d- диаметр окружности
C – длина
Слайд 29Задача:
1) вычислить длину окружности, если ее диаметр равен 6 см
2) вычислить
С = П D
С = 2П R
П ≈ 3,14
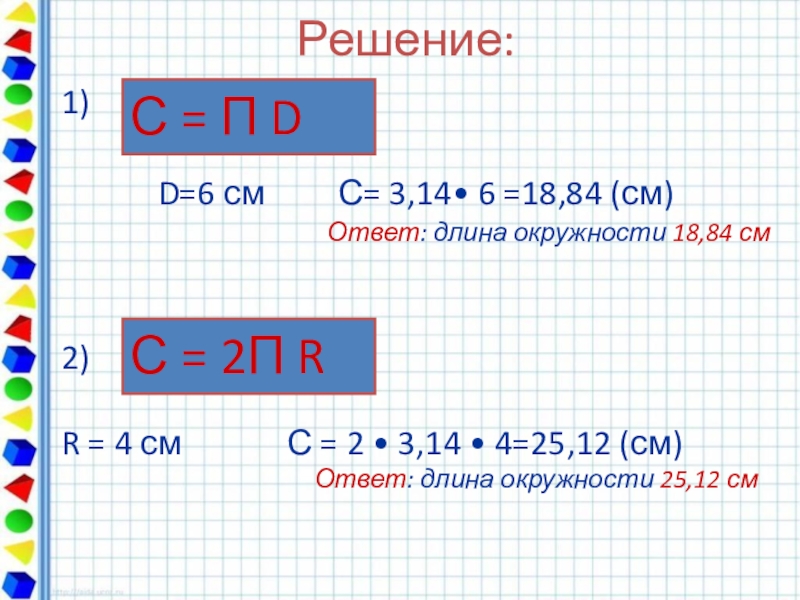
Слайд 30Решение:
1)
D=6 см С= 3,14• 6 =18,84 (см)
Ответ:
С = П D
С = 2П R
2)
R = 4 см С = 2 • 3,14 • 4=25,12 (см)
Ответ: длина окружности 25,12 см
Слайд 31Задача:
Длина окружности цирковой арены равна 41 м. Найдите
С = П D
С = 2П R
П ≈ 3,14
Слайд 32Решение:
С = П D
С=41 м
41 = 3,14•D
D = 41 :
D = 4100 : 314
D = 13 (м)
Ответ: диаметр цирковой арены равен 13 м
П = 3,14
Слайд 33Диаметр d= 5м
О
?
Длина окружности – С
Цветочная клумба имеет форму круга, диаметр
С = П D
П ≈ 3,14
С = 2П R
Слайд 35 Ныне самым старым деревом является гигантский кипарис, который растет в
Слайд 36Решите задачу
У лукоморья дуб зелёный;
Златая цепь на дубе том:
И днём и
Всё ходит по цепи кругом…
А.С.Пушкин
подсказка
ответ
С=0,03
d=0,01
S=0,000075
Слайд 37Решение
0,35 * 6 = 2,1 (км) прошел кот за 6
2,1 : 70 = 0,03 (км) длина 1 круга
Из формулы длины окружности найдем радиус
r=0,03:6 = 0, 005 (км)
d= 2* 0,005=0,01 (км)
S=3*0,000025=0,000075 (кв.км)
Слайд 38
Отлитый в 1735 г. Царь колокол, хранящийся
Диаметр колеса обозрения «Глаз Лондона» равен 135 м (рис. 96). Какой путь делает каждая из его гондол за один оборот вокруг центра колеса?
(Кстати, лондонское колесо обозрения самое большое в Европе. А слово «гондола» означает «кабина», а вообще гондолами называют особые лодки, в которых передвигаются жители Венеции по их улицам-рекам).
рис. 96
Слайд 39Решите задачу
Пришкольная площадка имеет форму квадрата периметром 96 м. посередине ее
Е.Ленский
ответ
Да, так как сторона квадрата больше диаметра окружности, описываемой веревкой и рукой
Слайд 40Решите задачу
Наконец и в путь обратный
Со своею силой ратной
И с девицей
Царь отправился домой…”
“Сказка о Золотом петушке”
ответ
0,3
Слайд 41Решите задачу
На побережье Средиземного моря растет интересное растение- так называемый стреляющий
Б.Друзь
Найди наибольшее расстояние, на которое могут улететь семена. Ответ округлите до десятых. Воспользуйся калькулятором.
ответ
3338,6 м
или
3,3 км
Слайд 42
Задача
(О Тунгусском метеорите, 1908 г.)
Слайд 43
Древнегреческий математик Архимед установил, что длина окружности относится к
Найдите длину окружности, диаметр которой 4,2 дм.
Слайд 44Верхушка головы -
Ноги прошли путь , где R радиус земного шара.
Вообразите, что вы обошли землю по экватору. На сколько при этом верхушка вашей головы прошла более длинный путь, чем кончик вашей ноги?
Решение.
Разность путей равна
Итак голова прошла путь на 10,7 м больше, чем ноги.
Ответ:10,7 м.
Слайд 45Обычно отвечают, что промежуток будет тоньше волоса.
Если обтянуть земной шар
Решение. Пусть длина промежутка х см.
Если R радиус земли, то длина проволоки была 2Rсм,
а станет 2 (R + x)см.
А по условию задачи их разность равна 100 см.
Уравнение.
Ответ:16 см.
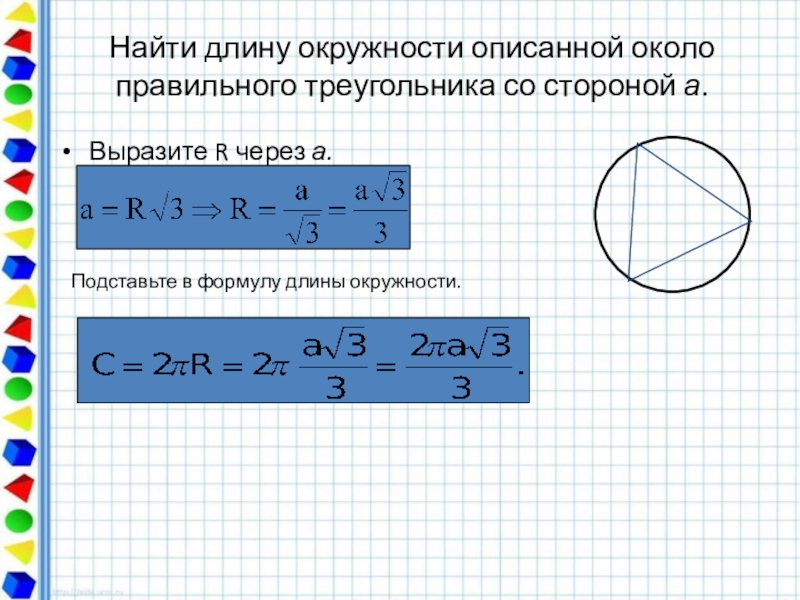
Слайд 46Найти длину окружности описанной около правильного треугольника со стороной а.
Выразите R
Подставьте в формулу длины окружности.
Слайд 47 R
R
H
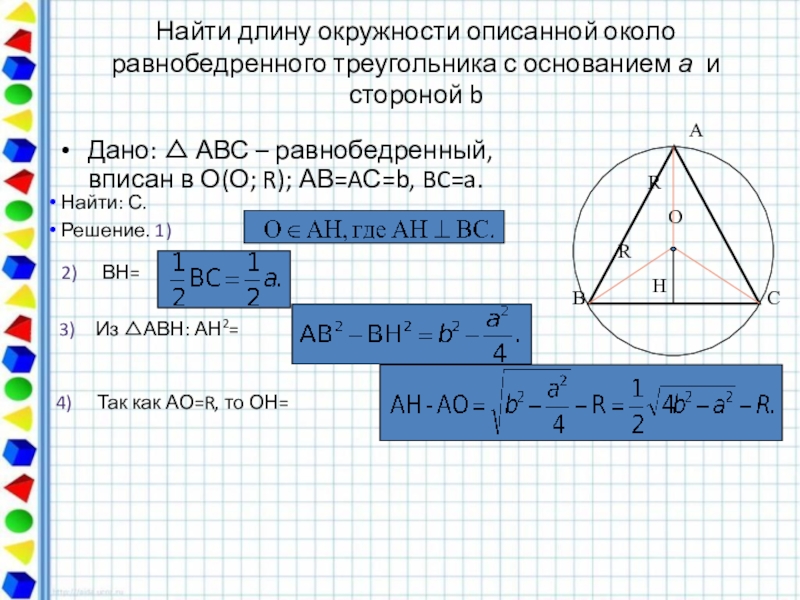
Дано: АВС – равнобедренный, вписан в О(О; R); АВ=AС=b, BC=a.
Найти длину окружности описанной около равнобедренного треугольника с основанием а и стороной b
А
В
С
ВН=
Из АВН: АН2=
Так как АО=R, то ОН=
Найти: С.
Решение. 1)
Слайд 48Найти длину окружности описанной около равнобедренного треугольника с основанием a и
Из ВОН: BО2=OH2+BH2=R2=
А
В
С
Н
C=
О
Ответ:
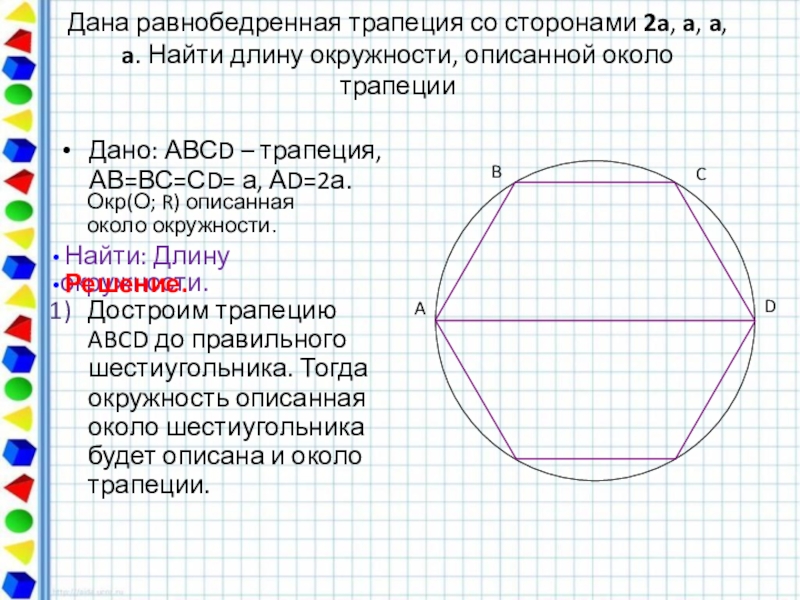
Слайд 49Дана равнобедренная трапеция со сторонами 2a, a, a, a. Найти длину
Дано: АВСD – трапеция, АВ=ВС=СD= а, АD=2а.
Найти: Длину окружности.
Решение.
Окр(О; R) описанная около окружности.
Достроим трапецию ABCD до правильного шестиугольника. Тогда окружность описанная около шестиугольника будет описана и около трапеции.
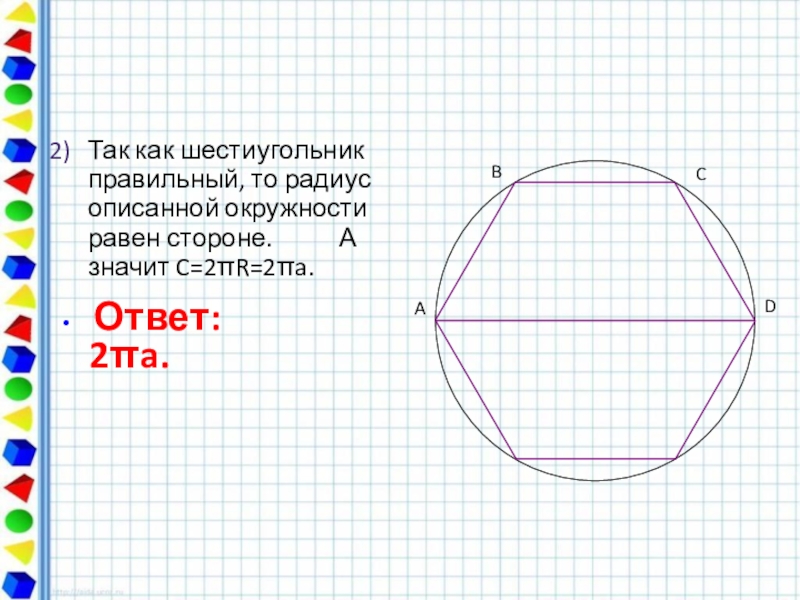
Слайд 50Так как шестиугольник правильный, то радиус описанной окружности равен стороне.
Ответ: 2a.
A
B
C
D
Слайд 51Архимед в III в. до н.э. обосновал в своей небольшой работе "Измерение круга"
всякий круг равновелик прямоугольному треугольнику, катеты которого соответственно равны длине окружности и её радиусу;
площади круга относятся к квадрату, построенному на диаметре, как 11 к 14;
отношение любой окружности к её
диаметру меньше 3 1/7 и больше 3 10/71.
Слайд 52В первой половине XV в. обсерватории Улугбека, возле Самарканда, астроном и
Только через 250 лет после ал-Каши
его результат был превзойдён.
Слайд 53Интересные факты
Отношение длины основания Великой Пирамиды к ее высоте,
Возможно, оно намеренно зашифровано в размерах Пирамиды Хеопса, причем с более точным значением, чем его знал великий Архимед, живший позже на 2000 лет!