- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Что такое симметрия
Содержание
- 1. Презентация по математике на тему Что такое симметрия
- 2. Цели: Узнать, присутствует ли симметрия в
- 3. Что такое симметрия?Симме́три́я (др.-греч. συμμετρία = «соразмерность»;
- 4. «Математика выявляет порядок, симметрию и определённость, а это важнейшие виды прекрасного» Аристотель(384-322 гг до н.э.)
- 5. Виды симметрии •Осевая (зеркальная) симметрия.•Центральная симметрия.•Поворотная симметрия.•Зеркально-поворотная симметрия.•Переносная (трансляционная) симметрия.•Скользящая плоскость(ось) симметрии.
- 6. Осевая (зеркальная) симметрия.•Фигура называется симметричной относительно прямой
- 7. Центральная симметрия.•Фигура называется симметричной относительно точки ,
- 8. Поворотная симметрия.Предположим, что объект совмещается сам с
- 9. Зеркально-поворотная симметрия.•Доказать, что существует такой вид симметрии,
- 10. Переносная (трансляционная) симметрия.•При переносе (трансляции) вдоль прямой
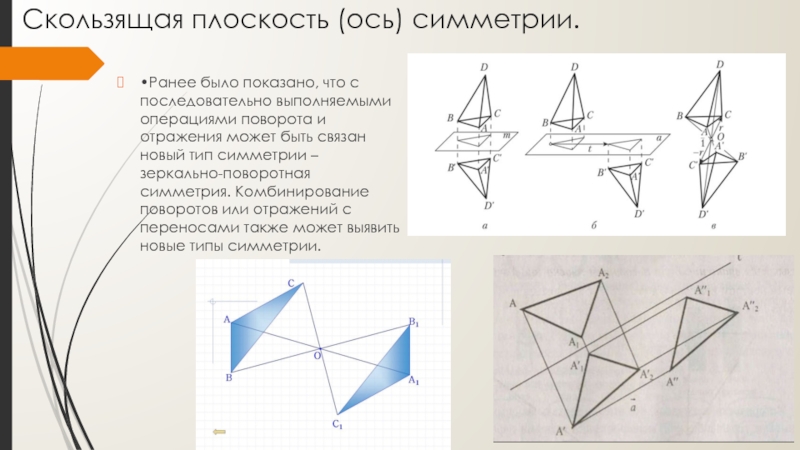
- 11. Скользящая плоскость (ось) симметрии.•Ранее было показано, что
- 12. Симметрия в архитектуре Ещё в древности
- 13. Архитектура – удивительная область человеческой деятельности.В ней
- 14. Симметрия в технике. Технические объекты – самолёты,
- 15. СИММЕТРИЯ В МУЗЫКЕМузыка –это радость души, которая
- 16. Симметрия в декоративно прикладном творчестве. Принцип симметрии
- 17. Симметрия в русском языке и литературе. Виды
- 18. Симметрия в природе 1. Брокколи романескоВозможно увидев
- 19. 3. ПодсолнухиПодсолнухи могут похвастаться радиальной симметрией и
- 20. 5. ЖивотныеБольшинство животных имеют двустороннюю симметрию, что
- 21. 7. Круги на поляхДайте паре обманщиков доску,
- 22. Слайд 22
Слайд 1Что такое симметрия?
Исаева Анна
обучающаяся 8 класса.
Наставник проекта:
Тихоновская
Анна Павловна
Слайд 2 Цели:
Узнать, присутствует ли симметрия в окружающем нас мире.
Задачи:
1.
Слайд 3Что такое симметрия?
Симме́три́я (др.-греч. συμμετρία = «соразмерность»; от συμ- «совместно» +
Слайд 4«Математика выявляет порядок, симметрию и определённость, а это важнейшие виды прекрасного»
Слайд 5Виды симметрии
•Осевая (зеркальная) симметрия.
•Центральная симметрия.
•Поворотная симметрия.
•Зеркально-поворотная симметрия.
•Переносная (трансляционная) симметрия
.•Скользящая плоскость(ось)
Слайд 6Осевая (зеркальная) симметрия.
•Фигура называется симметричной относительно прямой а, если для каждой
Все знают, что увидеть зазеркальный двойник объекта совсем нетрудно. Достаточно поместить освещённый объект перед плоским зеркалом и заглянуть в это зеркало. Обычно считают, что наблюдаемый в зеркале двойник является точной копией самого объекта.
Слайд 7Центральная симметрия.
•Фигура называется симметричной относительно точки , если для каждой точки
•Простейшими фигурами, обладающими центральной симметрией, является окружность и параллелограмм . Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма -точка пересечения его диагоналей. Прямая также обладает центральной симметрией, однако в отличие от окружности и параллелограмма, которые имеют только один центр симметрии у прямой их бесконечно много -любая точка прямой является её центром симметрии. Примером фигуры, не имеющей центра симметрии, является треугольник.
Слайд 8Поворотная симметрия.
Предположим, что объект совмещается сам с собой при повороте вокруг
Слайд 9Зеркально-поворотная симметрия.
•Доказать, что существует такой вид симметрии, мы предлагаем вам самим.
Слайд 10Переносная (трансляционная) симметрия.
•При переносе (трансляции) вдоль прямой АВ на расстояние а
Слайд 11Скользящая плоскость (ось) симметрии.
•Ранее было показано, что с последовательно выполняемыми операциями
Слайд 12Симметрия в архитектуре
Ещё в древности задачи архитектуры определяли тремя качествами
Слайд 13Архитектура – удивительная область человеческой деятельности.
В ней тесно переплетены и строго
Слайд 14Симметрия в технике.
Технические объекты – самолёты, автомашины, ракеты, молотки, гайки
Слайд 15СИММЕТРИЯ В МУЗЫКЕ
Музыка –это радость души, которая вычисляе , сама того
Ракоходное отражение - Примерами являются все мажорные и минорные гаммы кроме мелодического вида, а также некоторые отрывки произведений. Например, песня "Священная война" композитора А.В. Александрова и поэта В.И. Лебедева-Кумача, И.С. Бах "Музыкальное приношение"
Ракоходное отражение - Ракоходное отражение -зеркальный вид симметрии в геометрии . В этом случае зеркальная плоскость ориентирована перпендикулярно к нотным линейкам. Отраженные ноты кажутся такими, какими они действительно выглядели бы в зеркале. Начиная от зеркальной плоскости, оригинал проигрывается в обратном направлении.
Обращение интервала - Это самый редко встречающийся вид. Обращение исходит из звуковой последовательности, которая испытывает зеркальное отражение в плоскости, параллельной средней линии нотного стана, так что направления музыкальных интервалов изменяются на обратные. Если мелодия (звуковой ряд) оригинала повышается, то в обращении -понижается на такой же интервал, и наоборот.
Обращение интервала - Примерами могут служить следующие отрывки произведений: "Тарантелла", "Концерт для фортепиано с оркестром" Г. Фоглер.
Ракоходное обращение - При этом в зеркальной части снова меняется направленность звукового ряда по высоте. Понижающаяся мелодия ракохода становится повышающейся, и наоборот.
Ракоходное обращение - Примером является " Концерт для фортепиано с оркестром" Г. Фоглер. трансляционный видТрансляционный вид –поворотный вид в геометрии. Это самый распространенный вид симметрии в музыке. В этом случае музыкальная фраза (мелодия или более крупные отрывки музыкального произведения) повторяется, оставаясь неизменной. Но в некоторых случаях возможна асимметрия, то есть отступление от оригинала, для красоты звучания. трансляционный видПримерами служат все песни, в которых куплет (припев) повторяется без изменения несколько раз. Например, песня "Катюша" М. Исаковского (слова), Блантера(музыка). Так же, произведения написанные в трехчастной форме.
Слайд 16Симметрия в декоративно прикладном творчестве.
Принцип симметрии используется в построении орнамента. Орнамент–
Слайд 17Симметрия в русском языке и литературе.
Виды симметрий:
Симметрия – оборотень (когда слово
НА В ЛОБ БОЛВАН; А РОЗА УПАЛА НА ЛАПУ АЗОРА (А.Фет); Я ИДУ С МЕЧЕМ СУДИЯ (А.Державин); У ЛИП ЛЕША НАШЕЛ ПИЛУ; ОКОЛО МИТИ МОЛОКО; НО НЕВИДИМ АРХАНГЕЛ МОРОЗ УЗОРОМ ЛЕГ НА ХРАМ И ДИВЕН ОН; А ЛОБ АРАПА ПАРАБОЛА.
бесконечная симметрия (когда можно вставить бесконечно много слов)
Я ДЯДЯ Я ДЯДЯ…Я ДЯДЯ; Я ТЕТЯ Я ТЕТЯ…Я ТЕТЯ; У РОЯЛЯ ЛЯ ЛЯ ЛЯ…ЛЯ РУ; КОРОСТЕЛИ ЛЕТЕЛИ ЛЕТЕЛИ…ЛЕТЕЛИ ЛЕТ СОРОК
вертикальная ось симметрии: А;Д;Л;М;П;Т;Ф;Ш.
горизонтальная ось симметрии: В;Е;З;К;С;Э;Ю
вертикальные и горизонтальные оси симметрии: Ж;Н;О;Х.
В литературных произведениях существует симметрия образов, положений, мышления.
В «Евгении Онегине» А.С.Пушкина мы наблюдаем симметрию положений: «Онегин, отвергнувший когда-то любовь Татьяны, сам через несколько лет вынужден испытывать горечь отвергнутой любви».
В трагедии А.С.Пушкина «Борис Годунов» прекрасно выписана симметрия образов.
Убийцу царственного наследника, занявшего престол, сменяет на троне такой же умный, такой же наглый и беспощадный убийца юноши-царевича.
Слайд 18Симметрия в природе
1. Брокколи романеско
Возможно увидев брокколи романеско в магазине,
2. Соты
На протяжении тысяч лет люди удивлялись идеальной гексагональной форме сот и спрашивали себя, как пчелы могут инстинктивно создать форму, которую люди могут воспроизвести только с помощью циркуля и линейки. Как и почему пчелы имеют страстное желание создавать шестиугольники? Математики считают, что это идеальная форма, которая позволяет им хранить максимально возможное количество меда, используя минимальное количество воска. В любом случае, все это продукт природы, и это чертовски впечатляет.
Слайд 193. Подсолнухи
Подсолнухи могут похвастаться радиальной симметрией и интересным типом симметрии, известной
4. Раковина Наутилуса
Помимо растений, некоторые животные, например Наутилус, отвечают последовательности Фибоначчи. Раковина Наутилуса закручивается в «спираль Фибоначчи». Раковина пытается поддерживать одну и ту же пропорциональную форму, что позволяет ей сохранять её на протяжении всей жизни (в отличие от людей, которые меняют пропорции на протяжении жизни). Не все Наутилусы имеют раковину, выстроенную по правилам Фибоначчи, но все они отвечают логарифмической спирали . Прежде, чем вы позавидуете моллюскам-математикам, вспомните, что они не делают этого специально, просто такая форма наиболее рациональна для них.
Слайд 205. Животные
Большинство животных имеют двустороннюю симметрию, что означает, что они могут
6. Паутина
Есть около 5000 типов пауков, и все они создают почти идеальное круговое полотно с радиальными поддерживающими нитями почти на равном расстоянии и спиральной тканью для ловли добычи. Ученые не уверены, почему пауки так любят геометрию, так как испытания показали, что круглое полотно не заманит еду лучше, чем полотно неправильной формы. Ученые предполагают, что радиальная симметрия равномерно распределяет силу удара, когда жертва попадает в сети, в результате чего получается меньше разрывов.
Слайд 217. Круги на полях
Дайте паре обманщиков доску, косилки и спасительную темноту,
8. Снежинки
Даже такие крошечные образования, как снежинки, регулируются законами симметрии, так как большинство снежинок имеет шестигранную симметрию. Это происходит в частности из-за того, как молекулы воды выстраиваются, когда затвердевают (кристаллизуются). Молекулы воды приобретают твердое состояние, образуя слабые водородные связи, они выравниваются в упорядоченном расположении, которое уравновешивает силы притяжения и отталкивания, формируя гексагональную форму снежинки. Но при этом каждая снежинка симметрична, но ни одна снежинка не похожа на другую. Это происходит потому, что падая с неба, каждая снежинка испытывает уникальные атмосферные условия, которые заставляют её кристаллы располагаться определенным образом.