Пребудет вечной истина, как скоро
Её познает слабый человек!
И ныне теорема Пифагора верна,
Как и в его далёкий век.
А. Шамиссо
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике для 8 класса Теорема Пифагора
Содержание
- 1. Презентация по математике для 8 класса Теорема Пифагора
- 2. Цели Доказать теорему Пифагора.2. Научить применять теорему Пифагора при решении задач.
- 3. Устная работаКакой треугольник называется прямоугольным ?Как называются
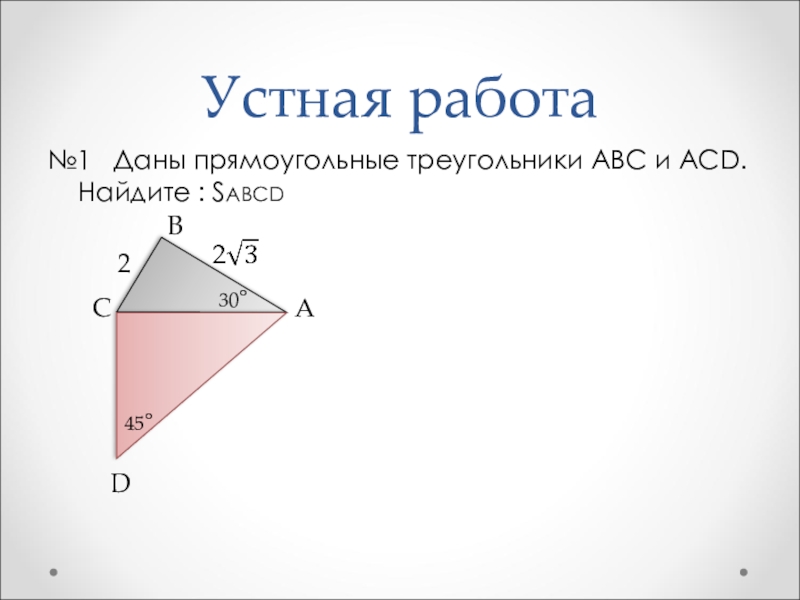
- 4. Устная работа№1 Даны прямоугольные треугольники ABC и ACD. Найдите : SABCD ABCD30° 245°
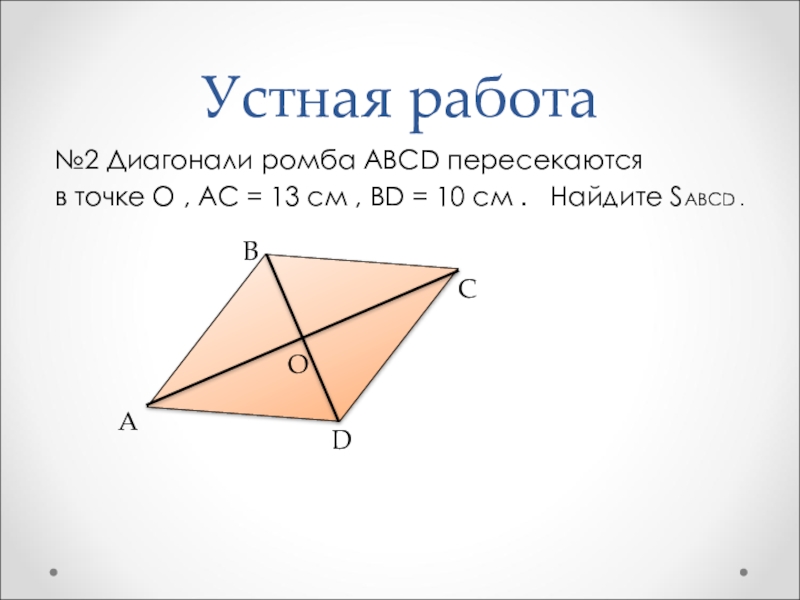
- 5. Устная работа №2 Диагонали ромба ABCD пересекаются
- 6. Существует замечательное соотношение между гипотенузой и катетами
- 7. История теоремы В настоящее время все согласны
- 8. О Пифагоре
- 9. Происхождение Пифагор родился в 570 году до
- 10. Заслуги Пифагора Пифагор славится как
- 11. Школа Пифагора Попасть в школу Пифагора
- 12. Стихи о Пифагоре. Немецкий писатель-романист А.
- 13. Теорема Пифагора В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов .cab
- 14. Доказательство : (древнекитайское)
- 15. Пифагоровы штаны Шуточное название теоремы
- 16. Египетский треугольникЕгипетский треугольник — прямоугольный треугольник с соотношением
- 17. Упражнения
- 18. Задача №1 Найти диагональ прямоугольника стороны которого равны 12 см и 5 см.АВСD
- 19. Задача №1 Найти диагональ прямоугольника стороны
- 20. Задача №2 Наш самолет пока находится
- 21. Задача №2 Наш самолет пока находится
- 22. На дом:П. 54 Выучить доказательство теоремы Пифагора.
- 23. СПАСИБО ЗА ВНИМАНИЕ
Цели Доказать теорему Пифагора.2. Научить применять теорему Пифагора при решении задач.
Слайд 1Теорема Пифагора
ГБОУ СОШ №1117 г. Москва
Учитель: Мелентьева И.А.
Слайд 3Устная работа
Какой треугольник называется прямоугольным ?
Как называются стороны образующие прямой угол
в треугольнике ?
Как называется сторона лежащая против прямого угла ?
Как называется сторона лежащая против прямого угла ?
Слайд 5Устная работа
№2 Диагонали ромба ABCD пересекаются
в точке O ,
AC = 13 см , BD = 10 см . Найдите SABCD .
A
B
C
D
O
Слайд 6Существует замечательное соотношение между гипотенузой и катетами прямоугольного треугольника , справедливость
которого была доказана древнегреческим философом и математиком Пифагором ( Vl в. До н.э. )
Историческая справка
Слайд 7История теоремы
В настоящее время все согласны с тем, что эта
теорема не была открыта Пифагором. Она была известна еще задолго до него. Ее знали в Китае, Вавилонии, Египте. Вернее, не ее, а частные случаи. Однако полагают, что Пифагор первым дал ее полноценное доказательство. В настоящее время известно более 100 доказательств.
Слайд 9Происхождение
Пифагор родился в 570 году до н. э на острове
Самос. Отцом Пифагора был Мнесарх – резчик по драгоценным камням. Имя матери Пифагора не сохранилось.
Многие считали, что Пифагор – это не имя, а прозвище. По многим античным свидетельствам, родившийся мальчик был удивительно красив, а вскоре проявил и свои незаурядные способности.
Среди учителей Пифагора были: старец Гермодамант и Ферекид Сиросский.
Многие считали, что Пифагор – это не имя, а прозвище. По многим античным свидетельствам, родившийся мальчик был удивительно красив, а вскоре проявил и свои незаурядные способности.
Среди учителей Пифагора были: старец Гермодамант и Ферекид Сиросский.
Слайд 10Заслуги Пифагора
Пифагор славится как известный математик и философ.
Он создал первую в Элладе философскую школу и проект первого театра. Кроме того, Пифагор разработал систему начального, среднего и высшего образования и содержание таких наук, как: грамматика, риторика, поэтика, арифметика, геометрия, астрономия и музыка.
Слайд 11Школа Пифагора
Попасть в школу Пифагора было непросто. Претендент должен
был выдержать ряд испытаний. Одним из таких испытаний являлся обет пятилетнего молчания, и все это время принятые в школу могли слушать голос учителя лишь из-за занавеса, а увидеть могли только тогда, когда их "души будут очищены музыкой и тайной гармонией чисел". Другим законом организации было хранение тайны, несоблюдение которой строго каралось.
Слайд 12Стихи о Пифагоре. Немецкий писатель-романист А. Шамиссо, который в начале Xl
X в. Участвовал в кругосветном путешествии на русском корабле «Рюрик», написал следующие стихи:
Пребудет вечной истина, как скоро
Её познает слабый человек!
И ныне теорема Пифагора
Верна, как и его далёкий век.
Обильно было жертвоприношение
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, её почуя, вслед.
Они не в силах свету помешать,
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор
Слайд 13Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме
квадратов катетов .
c
a
b
Слайд 14Доказательство : (древнекитайское)
На древнекитайском чертеже четыре
равных прямоугольных треугольника с катетами a, b и гипотенузой с уложены так, что их внешний контур образует квадрат со стороной a+b, а внутренний – квадрат со стороной с, построенный на гипотенузе.
Доказательства ТЕОРЕМЫ ПИФАГОРА.
Слайд 15Пифагоровы штаны
Шуточное название теоремы Пифагора, возникшее в силу
того, что раньше в школьных учебниках эта теорема доказывалась через доказательство равенства суммы площадей квадратов, построенных на катетах прямоугольного треугольника, площади квадрата, построенного на гипотенузе этого треугольника. Построенные на сторонах треугольника и расходящиеся в разные стороны квадраты напоминали школьникам покрой мужских штанов, что породило следующее стихотворение: «Пифагоровы штаны — на все стороны равны».
Слайд 16Египетский треугольник
Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5 активно применялся
для построения прямых углов египетскими землемерами и архитекторами, например, при построении пирамид.
Слайд 19Задача №1
Найти диагональ прямоугольника стороны которого равны 12 см
и 5 см.
А
В
С
D
Ответ : 13 см .
Слайд 20Задача №2
Наш самолет пока находится на высоте 6 км.
На земле мы преодолели расстояние 8 км. Какой путь пролетел самолёт в воздухе с момента взлёта?
Слайд 21Задача №2
Наш самолет пока находится на высоте 6 км.
На земле мы преодолели расстояние 8 км. Какой путь пролетел самолёт в воздухе с момента взлёта?
Ответ : 10 км.
Слайд 22На дом:
П. 54 Выучить доказательство теоремы Пифагора.
Выполнить задания № 483(б,в),
484(а), 486(в,б)
Творческое задание (по желанию) – найти другое доказательство теоремы Пифагора.
Творческое задание (по желанию) – найти другое доказательство теоремы Пифагора.