Светлана Петровна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике для 10 класса на тему Задачи на построение сечений
Содержание
- 1. Презентация по математике для 10 класса на тему Задачи на построение сечений
- 2. Проверка домашнего задания-С какими двумя многогранниками мы
- 3. Для решения многих геометрических задач, связанных с
- 4. Тема урока:Задачи на построение сечений
- 5. Цели урока-Давайте сформулируем цели нашего урока.
- 6. Секущая плоскость 1.Секущая плоскость тетраэдра(параллепипеда)-это любая плоскость,
- 7. Секущая плоскостьСечениеСекущая плоскость пересекает грани тетраэдра (параллелепипеда)
- 8. -Могут ли секущая плоскость и плоскость грани
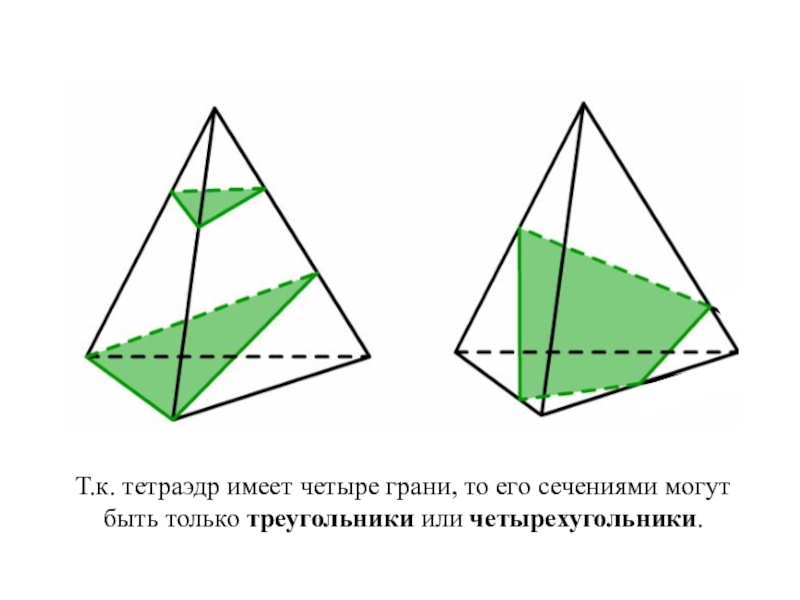
- 9. Т.к. тетраэдр имеет четыре грани, то его сечениями могут быть только треугольники или четырехугольники.
- 10. Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырехугольники, пятиугольники и шестиугольники.
- 11. КМFENПри построении сечений параллелепипеда на рисунке следует
- 12. Для построения сечения достаточно: 1)построить точки пересечения
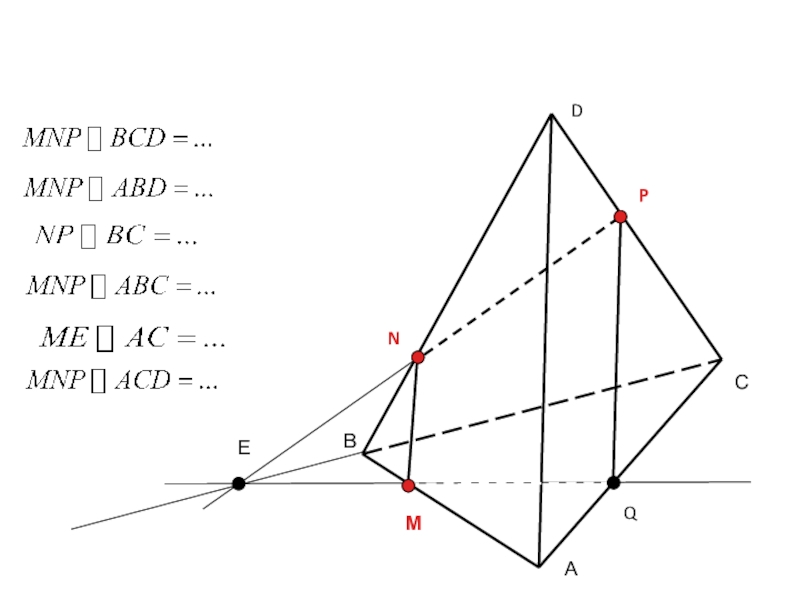
- 13. ВСАDNPМЗадача 1. На ребрах AB, BD и
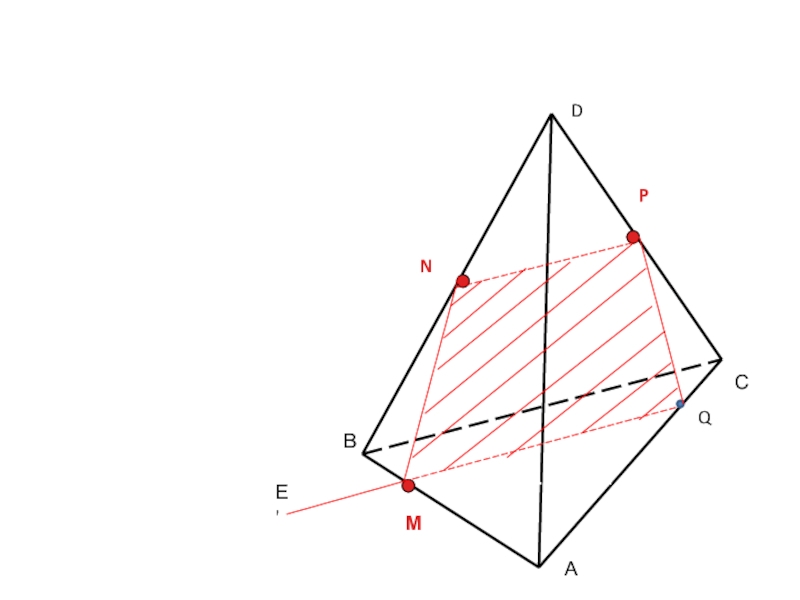
- 14. ВСАDNPМQЕ
- 15. ВСАDNPМQЕ'
- 16. ВСАDMЗадача 2. Точка М лежит на боковой
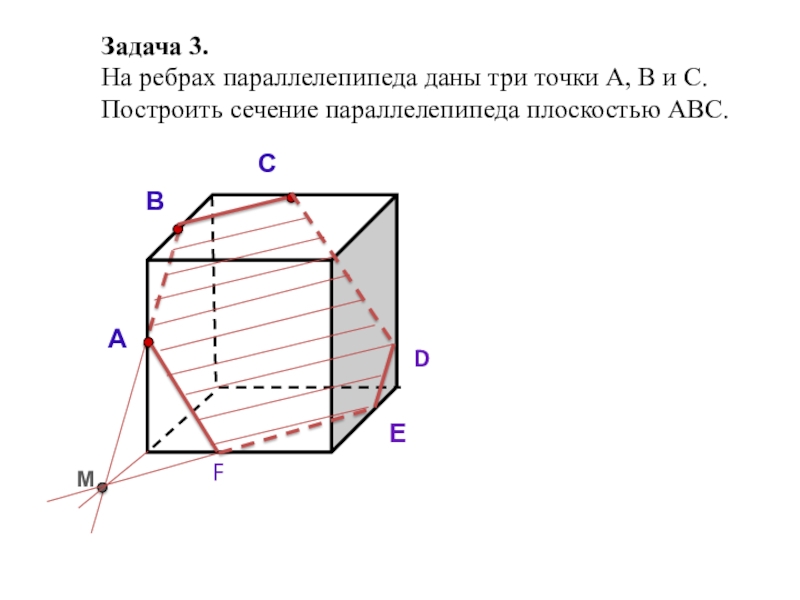
- 17. Задача 3. На ребрах параллелепипеда даны три
- 18. Задача 3. На ребрах параллелепипеда даны три
- 19. Задача 3. На ребрах параллелепипеда даны три
- 20. Задача №72(а). Изобразите тетраэдр DАВС и постройте
- 21. Задача №84. Изобразите параллелепипед АВСDА1В1С1D1 и постройте
- 22. Самостоятельная работаЗадача 1Постройте сечение тетраэдра ABCD плоскостью,
- 23. Задание: На ребрах взяты точки K,
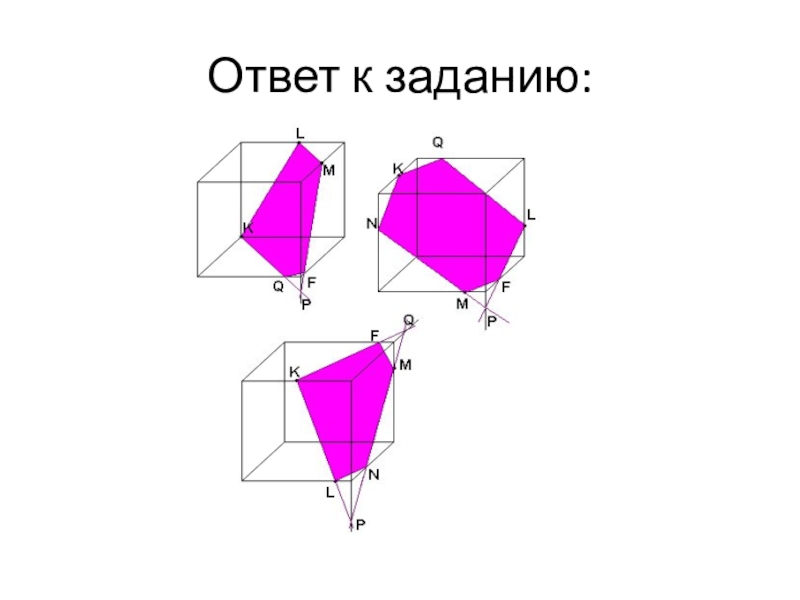
- 24. Ответ к заданию:
- 25. -Достигли ли мы поставленных
- 26. Домашнее заданиеП.14, подготовить презентацию на вопрос 15 учебника с.32;№72(б), №79(а);№106-индивидуально.
Проверка домашнего задания-С какими двумя многогранниками мы познакомились на прошлых уроках?-Что такое тетраэдр?(Второе название тетраэдра- треугольная пирамида).-Существует ли тетраэдр, у которого пять углов граней прямые?-Что такое параллелепипед?-Сформулируйте свойства параллелепипеда.
Слайд 2Проверка домашнего задания
-С какими двумя многогранниками мы познакомились на прошлых уроках?
-Что
такое тетраэдр?
(Второе название тетраэдра- треугольная пирамида).
-Существует ли тетраэдр, у которого пять углов граней прямые?
-Что такое параллелепипед?
-Сформулируйте свойства параллелепипеда.
(Второе название тетраэдра- треугольная пирамида).
-Существует ли тетраэдр, у которого пять углов граней прямые?
-Что такое параллелепипед?
-Сформулируйте свойства параллелепипеда.
Слайд 3Для решения многих геометрических задач, связанных с многогранниками, полезно уметь строить
на рисунке их сечения различными плоскостями.
Задача С2 из материалов ЕГЭ 2013 года:
В правильной четырехугольной пирамиде МАВСD с вершиной М стороны основания равны 6, а боковые ребра равны 5. Найдите площадь сечения пирамиды плоскостью, проходящей через точку А и середину ребра МС.
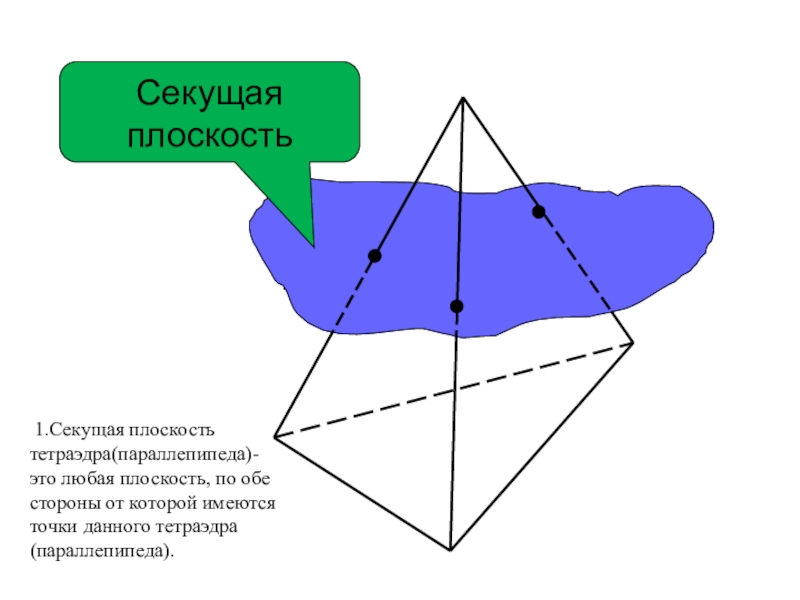
Слайд 6Секущая плоскость
1.Секущая плоскость тетраэдра(параллепипеда)-это любая плоскость, по обе стороны от
которой имеются точки данного тетраэдра (параллепипеда).
Слайд 7Секущая плоскость
Сечение
Секущая плоскость пересекает грани тетраэдра (параллелепипеда) по отрезкам.
Многоугольник, сторонами
которого являются эти отрезки, называется сечением тетраэдра (параллелепипеда).
Слайд 8-Могут ли секущая плоскость и плоскость грани многогранника быть параллельными друг
другу?
-Значит, нам нужно повторить свойства параллельных плоскостей , признак параллельности двух плоскостей?
Признак параллельности прямой и плоскости?
-Значит, нам нужно повторить свойства параллельных плоскостей , признак параллельности двух плоскостей?
Признак параллельности прямой и плоскости?
Слайд 9Т.к. тетраэдр имеет четыре грани, то его сечениями могут быть только
треугольники или четырехугольники.
Слайд 10Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырехугольники, пятиугольники
и шестиугольники.
Слайд 11К
М
F
E
N
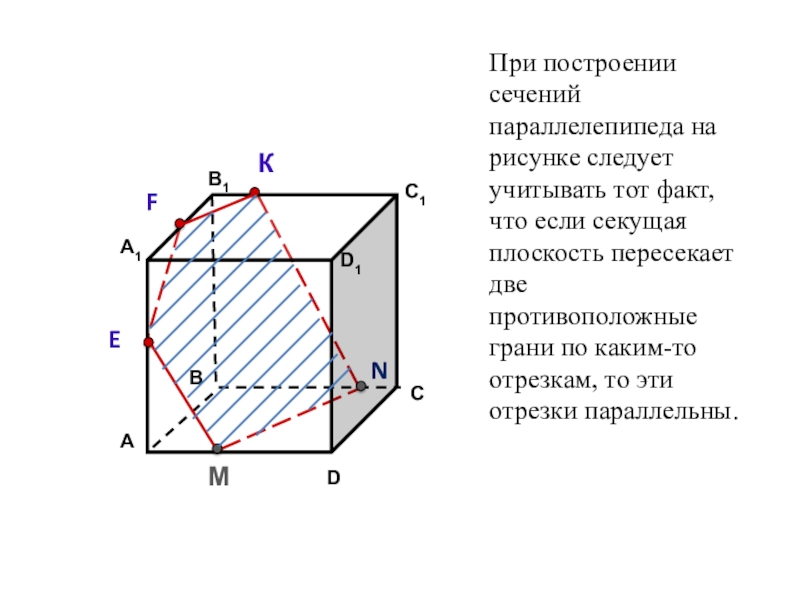
При построении сечений параллелепипеда на рисунке следует учитывать тот факт, что
если секущая плоскость пересекает две противоположные грани по каким-то отрезкам, то эти отрезки параллельны.
Слайд 12Для построения сечения достаточно:
1)построить точки пересечения секущей плоскости с ребрами
тетраэдра (параллелепипеда);
2) провести отрезки, соединяющие каждые две построенные точки, лежащие в одной и той же грани.
2) провести отрезки, соединяющие каждые две построенные точки, лежащие в одной и той же грани.
Слайд 13В
С
А
D
N
P
М
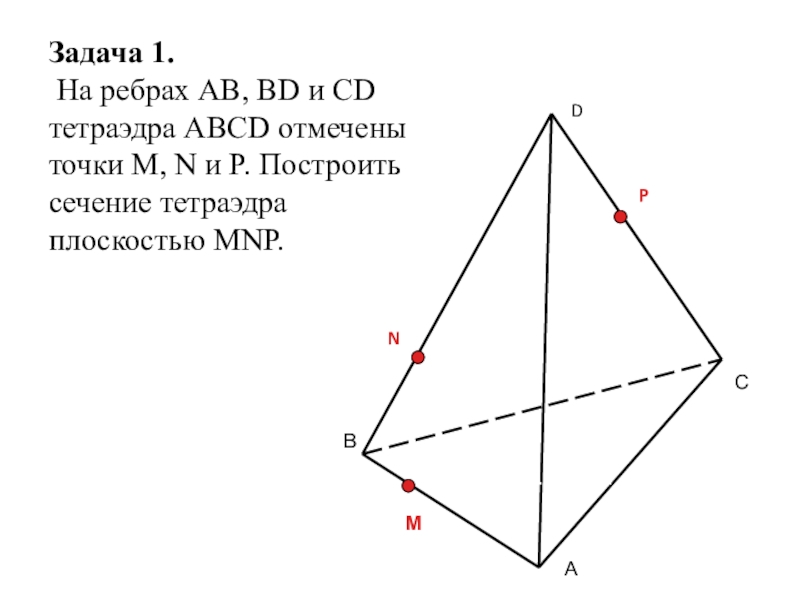
Задача 1.
На ребрах AB, BD и CD тетраэдра ABCD отмечены
точки M, N и P. Построить сечение тетраэдра плоскостью MNP.
Слайд 16В
С
А
D
M
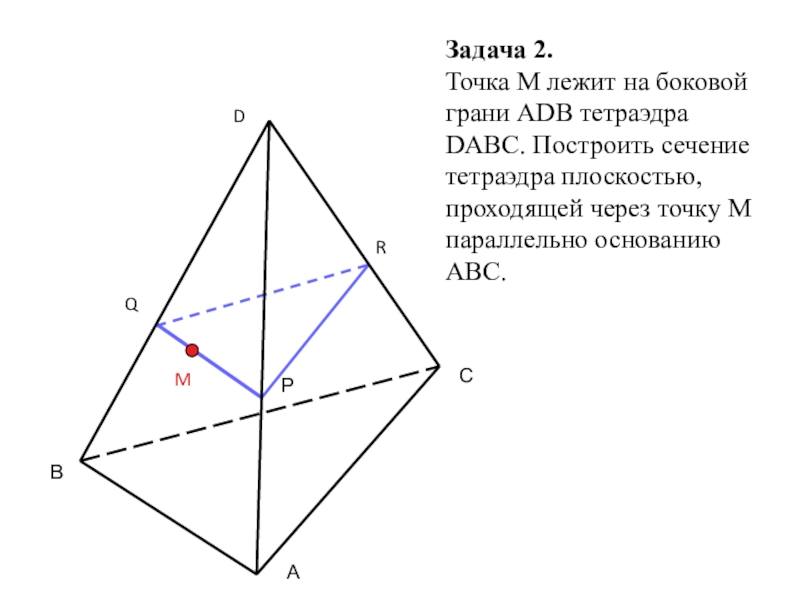
Задача 2.
Точка М лежит на боковой грани АDВ тетраэдра DАВС.
Построить сечение тетраэдра плоскостью, проходящей через точку М параллельно основанию АВС.
Q
Р
R
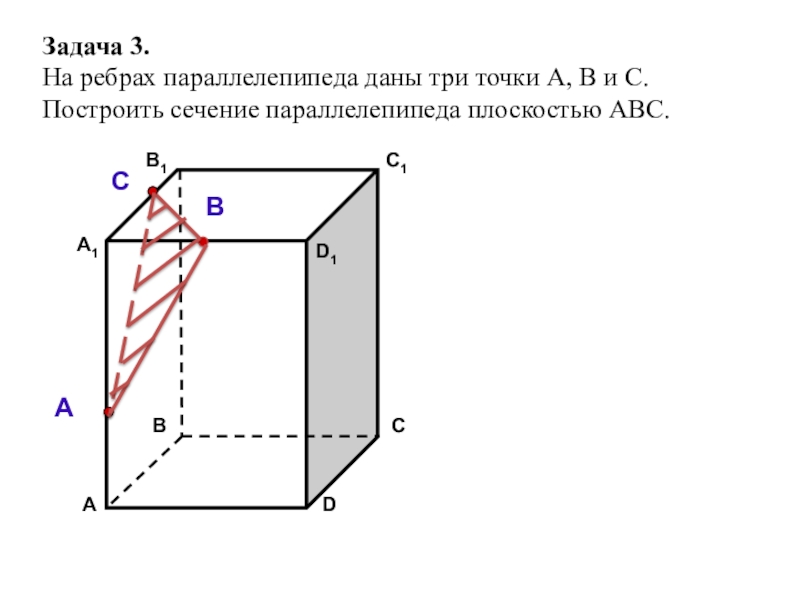
Слайд 17Задача 3.
На ребрах параллелепипеда даны три точки А, В и
С. Построить сечение параллелепипеда плоскостью АВС.
В
С
А
Слайд 18Задача 3.
На ребрах параллелепипеда даны три точки А, В и
С. Построить сечение параллелепипеда плоскостью АВС.
В
С
А
D
Е
Слайд 19Задача 3.
На ребрах параллелепипеда даны три точки А, В и
С. Построить сечение параллелепипеда плоскостью АВС.
С
М
F
В
А
D
Е
Слайд 20Задача №72(а). Изобразите тетраэдр DАВС и постройте сечение этого тетраэдра плоскостью,
проходящей через точку М параллельно плоскости грани АВС, если: а) точка М является серединой ребра АD.
A
B
C
D
M
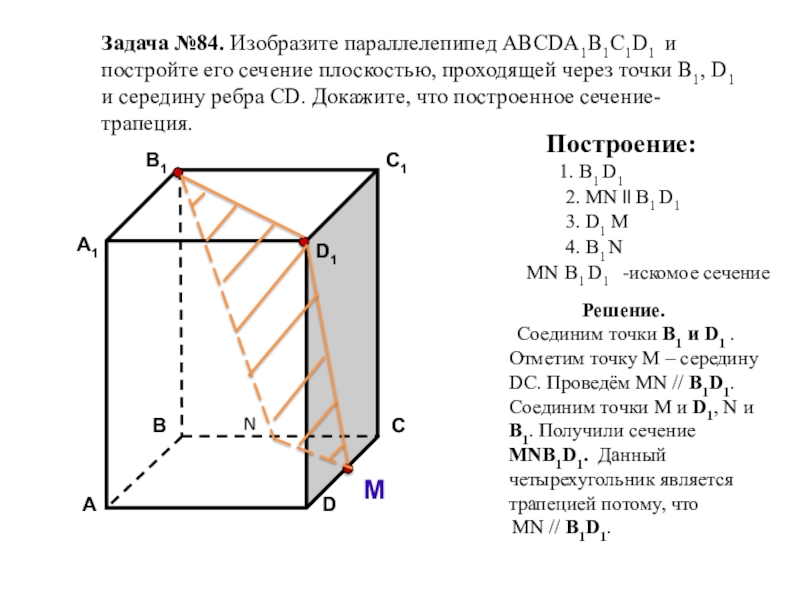
Слайд 21Задача №84. Изобразите параллелепипед АВСDА1В1С1D1 и постройте его сечение плоскостью, проходящей
через точки В1, D1 и середину ребра СD. Докажите, что построенное сечение- трапеция.
М
Построение:
N
1. В1 D1
3. D1 М
2. МN ll В1 D1
МN В1 D1 -искомое сечение
Решение.
Соединим точки В1 и D1 . Отметим точку М – середину DC. Проведём MN // В1D1. Соединим точки M и D1, N и В1. Получили сечение МNВ1D1. Данный четырехугольник является трапецией потому, что
MN // В1D1.
4. В1 N
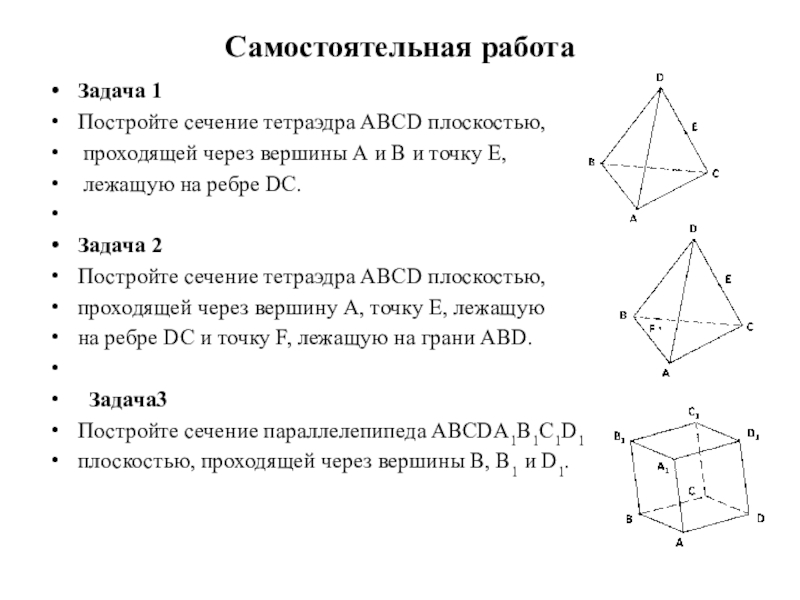
Слайд 22Самостоятельная работа
Задача 1
Постройте сечение тетраэдра ABCD плоскостью,
проходящей через вершины А
и В и точку Е,
лежащую на ребре DC.
Задача 2
Постройте сечение тетраэдра ABCD плоскостью,
проходящей через вершину А, точку Е, лежащую
на ребре DC и точку F, лежащую на грани ABD.
Задача3
Постройте сечение параллелепипеда ABCDA1B1C1D1
плоскостью, проходящей через вершины В, В1 и D1.
лежащую на ребре DC.
Задача 2
Постройте сечение тетраэдра ABCD плоскостью,
проходящей через вершину А, точку Е, лежащую
на ребре DC и точку F, лежащую на грани ABD.
Задача3
Постройте сечение параллелепипеда ABCDA1B1C1D1
плоскостью, проходящей через вершины В, В1 и D1.
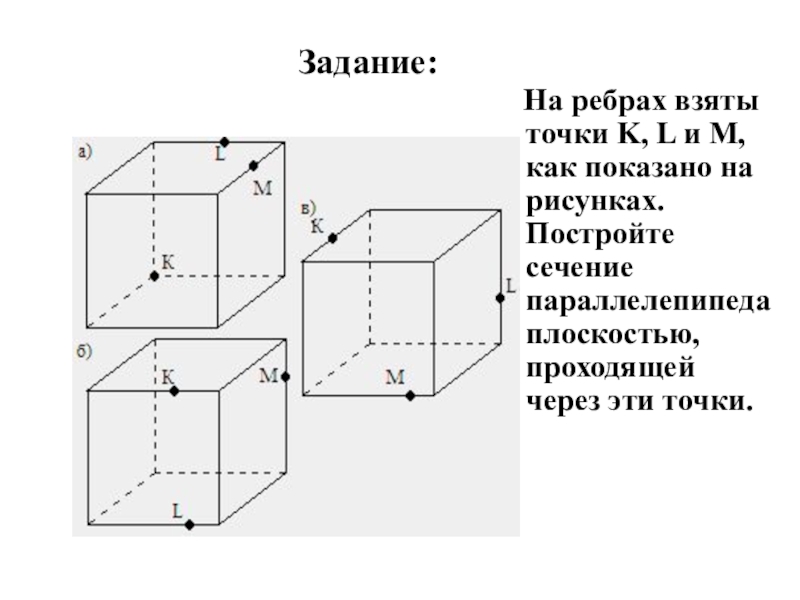
Слайд 23Задание:
На ребрах взяты точки K, L и M, как
показано на рисунках. Постройте сечение параллелепипеда плоскостью, проходящей через эти точки.
Слайд 25 -Достигли ли мы поставленных целей урока?
Что такое секущая
плоскость?
Что такое сечение многогранника?
Что значит построить сечение многогранника плоскостью?
Что получается при пересечении тетраэдра плоскостью сечения?
Какие многоугольники можно получить в сечении параллелепипеда плоскостью?
Что такое сечение многогранника?
Что значит построить сечение многогранника плоскостью?
Что получается при пересечении тетраэдра плоскостью сечения?
Какие многоугольники можно получить в сечении параллелепипеда плоскостью?
Слайд 26Домашнее задание
П.14, подготовить презентацию на вопрос 15 учебника с.32;
№72(б), №79(а);
№106-индивидуально.
