- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по итоговому повторению за курс геометрии 10-11 класса
Содержание
- 1. Презентация по итоговому повторению за курс геометрии 10-11 класса
- 2. А1CBАB1C16см3смДано:АВСА1В1С1 – правильная призмарёбра основания – 6см,
- 3. А1CBАB1C16см3см1. Найти площадь сечения призмы плоскостью АВС1
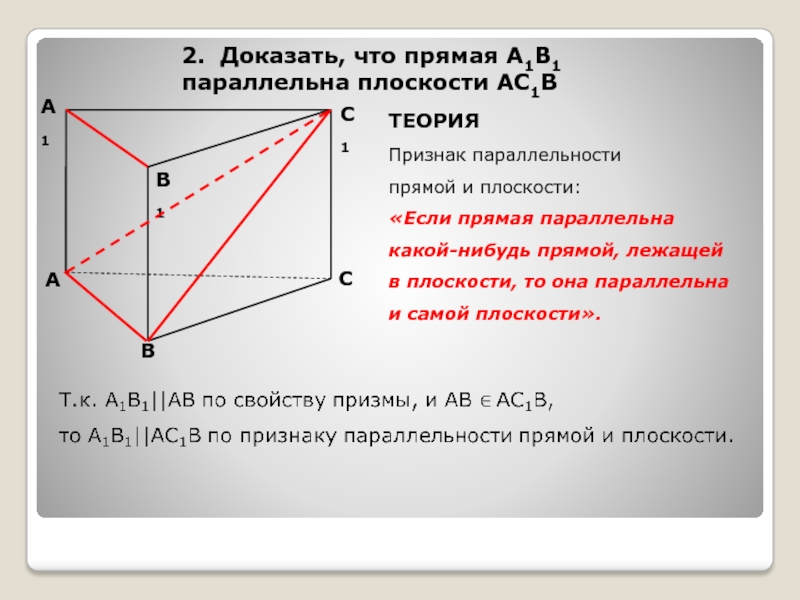
- 4. А1CBАB1C12. Доказать, что прямая А1В1 параллельна плоскости
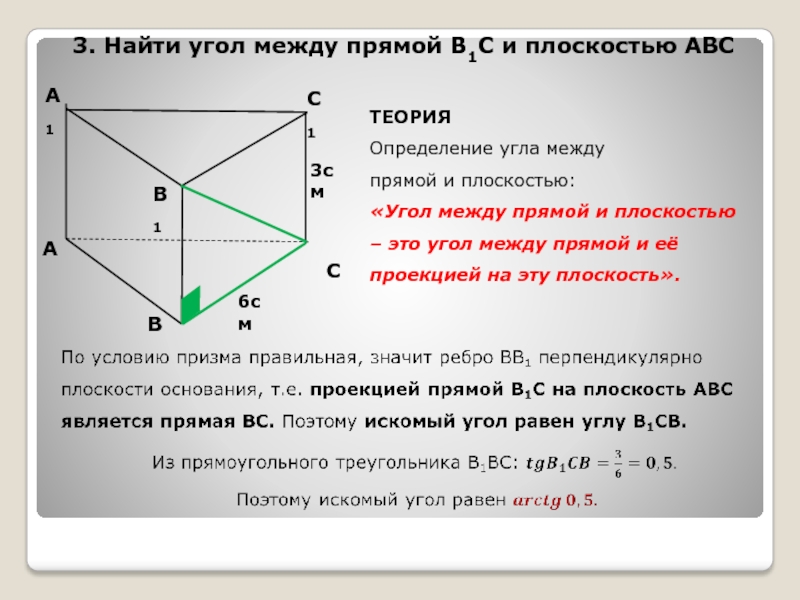
- 5. А1CBАB1C13см3. Найти угол между прямой В1С и
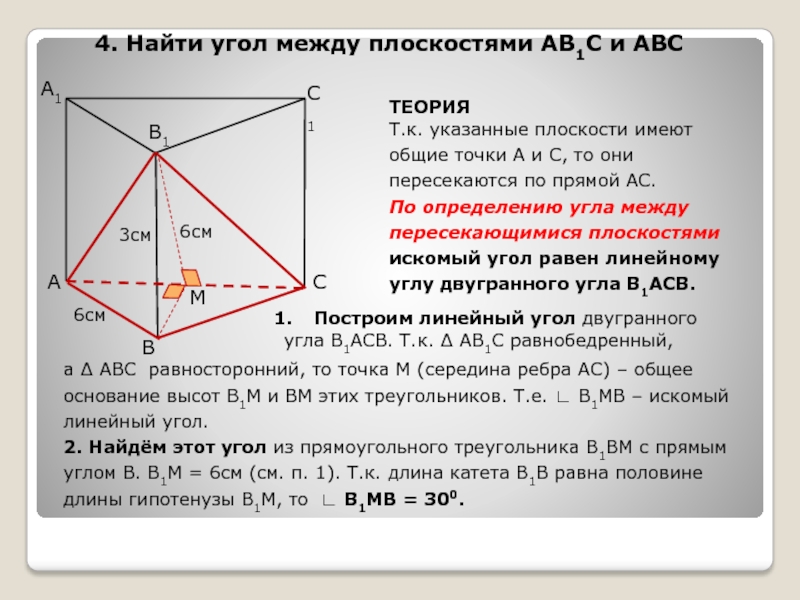
- 6. А1CBАB1C16см3см4. Найти угол между плоскостями АВ1С и
- 7. А1CBАB1C16см5. Найти длину вектора ВВ1 – ВС
- 8. А1CBАB1C16см3см6. Найти объём призмы
Слайд 2А1
C
B
А
B1
C1
6см
3см
Дано:
АВСА1В1С1 – правильная призма
рёбра основания – 6см, боковые рёбра – 3см
1) найти Sсеч. плоскостью АВС1
2) доказать: А1В1||AC1B
3) найти угол между В1С и АВС
4) найти угол между АВ1С и АВС
5) найти длину вектора
ВВ1 – ВС + 2А1А – С1С
6) найти объём призмы
Слайд 3А1
C
B
А
B1
C1
6см
3см
1. Найти площадь сечения призмы плоскостью АВС1
1) Построим сечение –
треугольник АВС1.
6см
Н
Слайд 4А1
C
B
А
B1
C1
2. Доказать, что прямая А1В1
параллельна плоскости АC1B
ТЕОРИЯ
Признак параллельности
прямой и плоскости:
«Если прямая
какой-нибудь прямой, лежащей
в плоскости, то она параллельна
и самой плоскости».
Слайд 5А1
C
B
А
B1
C1
3см
3. Найти угол между прямой В1С и плоскостью АВС
ТЕОРИЯ
Определение угла между
прямой
«Угол между прямой и плоскостью – это угол между прямой и её
проекцией на эту плоскость».
6см
Слайд 6А1
C
B
А
B1
C1
6см
3см
4. Найти угол между плоскостями АВ1С и АВС
ТЕОРИЯ
Т.к. указанные плоскости имеют
общие точки А и С, то они пересекаются по прямой АС.
По определению угла между
пересекающимися плоскостями
искомый угол равен линейному
углу двугранного угла В1АСВ.
М
а ∆ АВС равносторонний, то точка М (середина ребра АС) – общее основание высот В1М и ВМ этих треугольников. Т.е. ∟ В1МВ – искомый линейный угол.
2. Найдём этот угол из прямоугольного треугольника В1ВМ с прямым
углом В. В1М = 6см (см. п. 1). Т.к. длина катета В1В равна половине
длины гипотенузы В1М, то ∟ В1МВ = 300.
6см
Построим линейный угол двугранного
угла В1АСВ. Т.к. ∆ АВ1С равнобедренный,
Слайд 7А1
C
B
А
B1
C1
6см
5. Найти длину вектора ВВ1 – ВС + 2А1А – С1С
ТЕОРИЯ (определения и свойства
действий с векторами)
По определению равных векторов: А1А = В1В.
По определению суммы векторов: СВ1 + В1В = СВ.
По определение разности векторов:ВВ1 – ВС = СВ1.
По определению произведения
вектора на число: 2А1А = А1А + А1А.
Кроме этого, выполняются переместительное
и сочетательное свойства.