- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике языку на тему Пифагорская школа (10 класс)
Содержание
- 1. Презентация по информатике языку на тему Пифагорская школа (10 класс)
- 2. Повторим значения синуса косинуса
- 3. Арксинус
- 4. Арккосинус0π1-1arccos(-а)Арккосинусом числа а называется такое число (угол)
- 5. При каких значениях х имеет смысл выражение:1.arcsin(2x+1)2.arccos(5-2x)3.arccos(x²-1)4.arcsin(4x²-3x)1)
- 6. Повторим значения тангенса и котангенсаЛиния тангенсов
- 7. Арктангенс0arctgа = tАрктангенсом числа а называетсятакое число
- 8. Арккотангенсух0πarcctg а = tАрккотангенсом числа а называетсятакое
- 9. Формулы корней простых тригонометрических уравнений1.cost = а
- 10. Примеры:1) cost= - ½;2) sint = 0;3)
- 11. Решение простейших уравненийtg2x = -1
- 12. Другие тригонометрические уравнения1.Сводимые к квадратным
- 13. Простые тригонометрические неравенства1) cost > аОтвет: (-arccos
Слайд 2Повторим значения синуса косинуса
120° 2π/3 1 π/3 60°
135° 3π/4 π/4 45°
150° 5π/6 1/2 π/6 30°
180° π -1 0 1 0 0° x
- - -1/2 ½ 2π 360 (cost)
210° 7π/6 -1/2 11π/6 330° [-π/6]
-
225° 5π/4 - 7π/4 315° [-π/4]
240° 4π/3 -1 5π/3 300° [-π/3]
270° 3π/2 [-π/2]
(sint)
Слайд 3Арксинус
Примеры:
а
- а
arcsin(- а)= - arcsin а
Арксинусом числа а называется
такое число (угол) t из [-π/2;π/2],
что sin t = а.
Причём, | а |≤ 1.
Слайд 4Арккосинус
0
π
1
-1
arccos(-а)
Арккосинусом числа а называется
такое число (угол) t из [0;π], что
cos
Причём, | а |≤ 1.
arccos(- а) = π- arccos а
Примеры:
1)arccos(-1)
= π
![Арккосинус0π1-1arccos(-а)Арккосинусом числа а называется такое число (угол) t из [0;π], чтоcos t = а. Причём, | а](/img/thumbs/aaf2404c4513a873c73f59ce9a3ec8e8-800x.jpg "Презентация по информатике языку на тему Пифагорская школа (10 класс) Арккосинус0π1-1arccos(-а)Арккосинусом числа а называется такое число (угол) t из [0;π], чтоcos")
Слайд 5При каких значениях х имеет смысл выражение:
1.arcsin(2x+1)
2.arccos(5-2x)
3.arccos(x²-1)
4.arcsin(4x²-3x)
1) -1≤ 2х-1 ≤1
-1≤ х ≤0
Ответ: [-1;0]
2) -1≤ 5-2х ≤1
-6≤ -2х ≤ -4
2≤ х ≤3
Ответ: [2;3]
Слайд 6Повторим значения тангенса и котангенса
Линия тангенсов
у π/2
2π/3 π/3 1
5π/6 π/4
π/6 ctg t ЄR, но t ‡ 0 + πk, kЄZ
0 х Линия котангенсов
у
4π/3
-π/2
π 0 х
Слайд 7Арктангенс
0
arctgа = t
Арктангенсом числа а называется
такое число (угол) t из (-π/2;π/2),
что tg t = а .
Причём, а Є R.
arctg(-а) = - arctg а
-а
arctg(-а )
Примеры:
1) arctg√3/3 =
π/6
2) arctg(-1) =
-π/4
Слайд 8Арккотангенс
у
х
0
π
arcctg а = t
Арккотангенсом числа а называется
такое число (угол) t из
что ctg t = а.
Причём, а ЄR .
arcctg(- а) = π – arcctg а
- а
arcctg(- а)
1) arcctg(-1) =
Примеры:
3π/4
2) arcctg√3 =
π/6
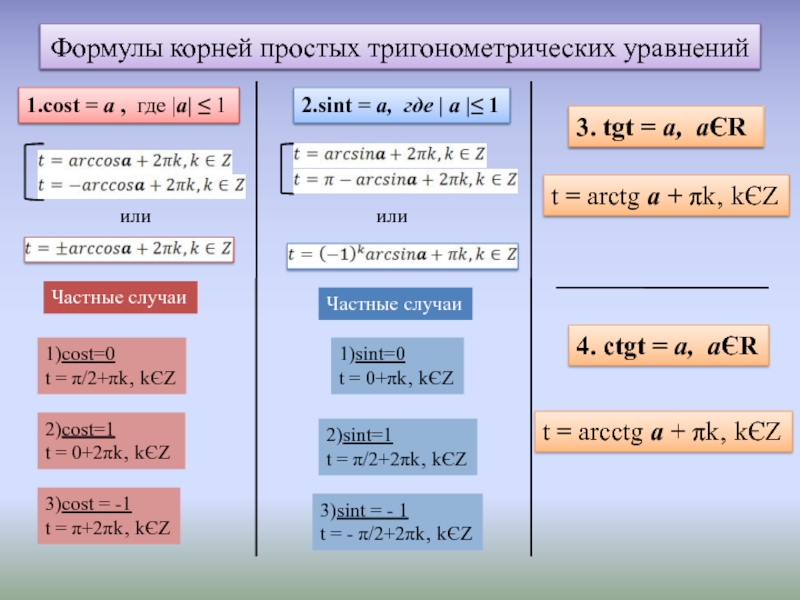
Слайд 9Формулы корней простых тригонометрических уравнений
1.cost = а , где |а| ≤
или
Частные случаи
1)cost=0
t = π/2+πk‚ kЄZ
2)cost=1
t = 0+2πk‚ kЄZ
3)cost = -1
t = π+2πk‚ kЄZ
2.sint = а, где | а |≤ 1
или
Частные случаи
1)sint=0
t = 0+πk‚ kЄZ
2)sint=1
t = π/2+2πk‚ kЄZ
3)sint = - 1
t = - π/2+2πk‚ kЄZ
3. tgt = а, аЄR
t = arctg а + πk‚ kЄZ
4. ctgt = а, аЄR
t = arcctg а + πk‚ kЄZ
Слайд 10Примеры:
1) cost= - ½;
2) sint = 0;
3) tgt = 1;
t= ±arccos(-1/2)+2πk,
t= ±2π/3+2πk, kЄZ
Частный случай:
t = 0+πk, kЄZ
t = arctg1+πk, kЄZ
t = π/4+πk, kЄZ.
Слайд 11Решение простейших уравнений
tg2x = -1
2x = arctg (-1)
2x = -π/4 + πk, kЄZ
x = -π/8 + πk/2, kЄZ
Ответ: -π/8 + πk/2, kЄZ.
2) cos(x+π/3) = ½
x+π/3 = ±arccos1/2 + 2πk, kЄZ
x+π/3 = ±π/3 + 2πk, kЄZ
x = -π/3 ± π/3 + 2πk, kЄZ
Ответ: -π/3 ± π/3 + 2πk, kЄZ
3) sin(π – x/3) = 0
упростим по формулам приведения
sin(x/3) = 0
частный случай
x/3 = πk, kЄZ
x = 3πk, kЄZ.
Ответ: 3πk, kЄZ.
Слайд 12Другие тригонометрические уравнения
1.Сводимые к квадратным
a∙sin²x +
Пусть sinx = p, где |p| ≤1, тогда
a∙p² + b∙p + c = 0
Найти корни, вернуться к замене и
решить простые уравнения.
2.Однородные
1)Первой степени:
a∙sinx + b∙cosx = 0
Т.к. sinx и cosx одновременно
не равны нулю, то разделим обе
части уравнения на cosx. Получим:
простое уравнение
a∙tgx + b = 0 или tgx = m
2)Второй степени:
a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0
Разделим обе части на cos²x.
Получим квадратное уравнение:
a∙tg²x + b∙tgx + c = 0.
Слайд 13Простые тригонометрические неравенства
1) cost > а
Ответ: (-arccos а+2πk; arccos а+2πk), kЄZ
2)
Ответ: (-(π+arcsin а)+2πk; arcsin а+2πk), kЄZ
3) tgt > -а
Ответ: (-arctg а+πk; π/2+πk), kЄZ
4) ctgt > а
Ответ: (0+πk; arcctg а+πk), kЄZ.
