Презентация, доклад по геометрии Вписанные и описанные цилиндры по теме (11 класс )

Содержание

Упражнение 1В цилиндр высоты 2 вписана сфера. Найдите ее радиус.Ответ: 1.

Слайд 1Сфера, вписанная в цилиндр
Сфера называется вписанной в цилиндр, если она касается

его оснований и боковой поверхности (касается каждой образующей). При этом цилиндр называется описанным около сферы.

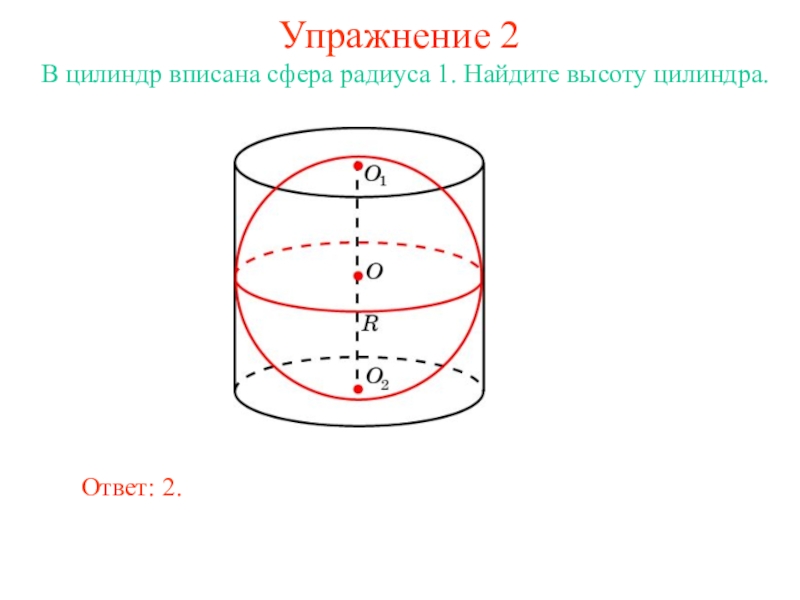
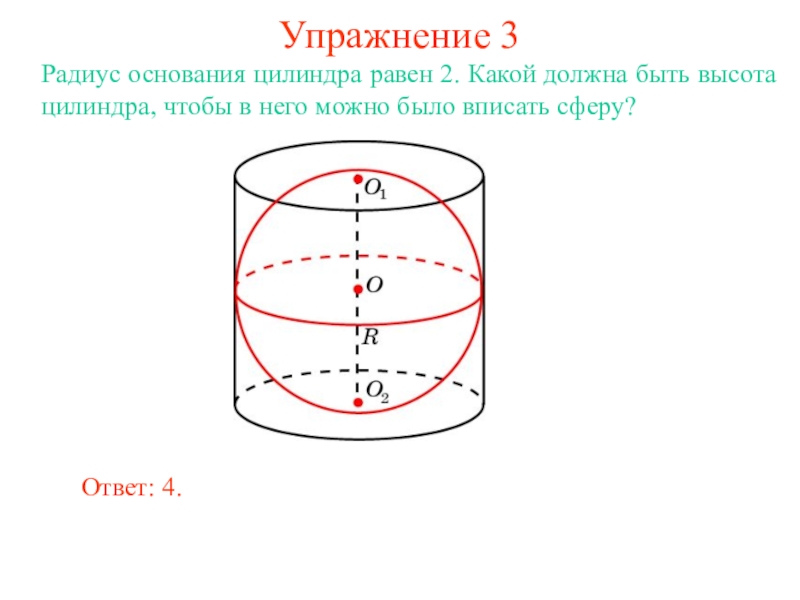
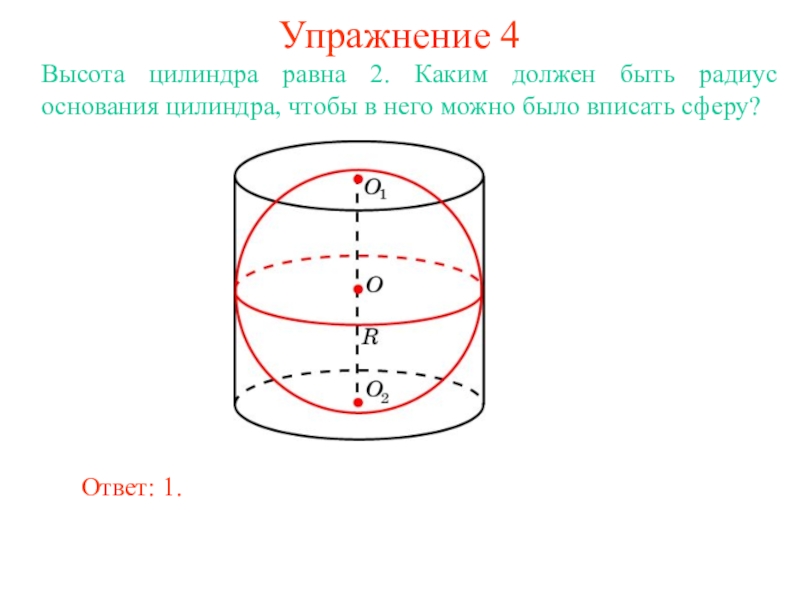
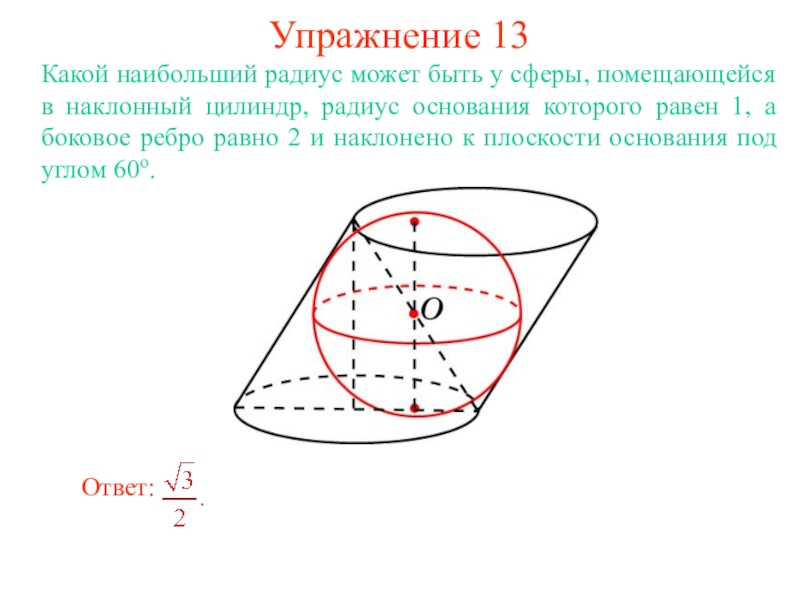
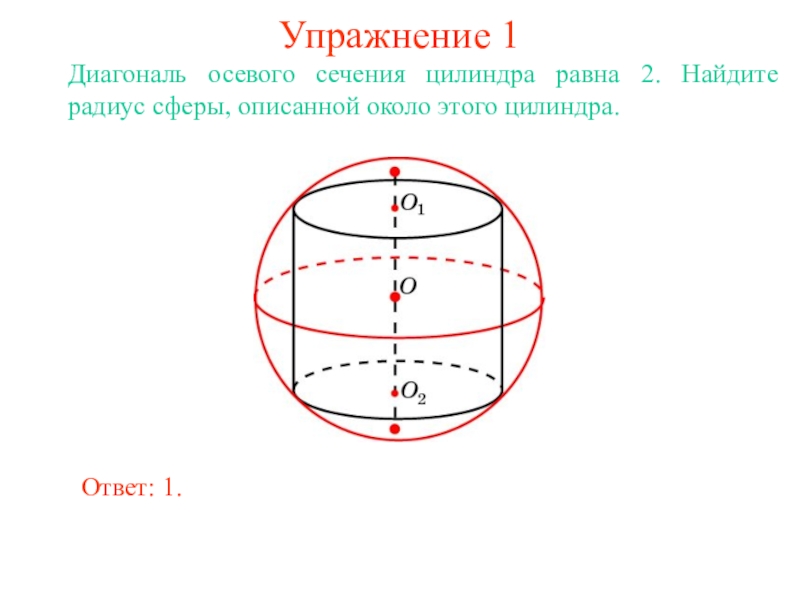
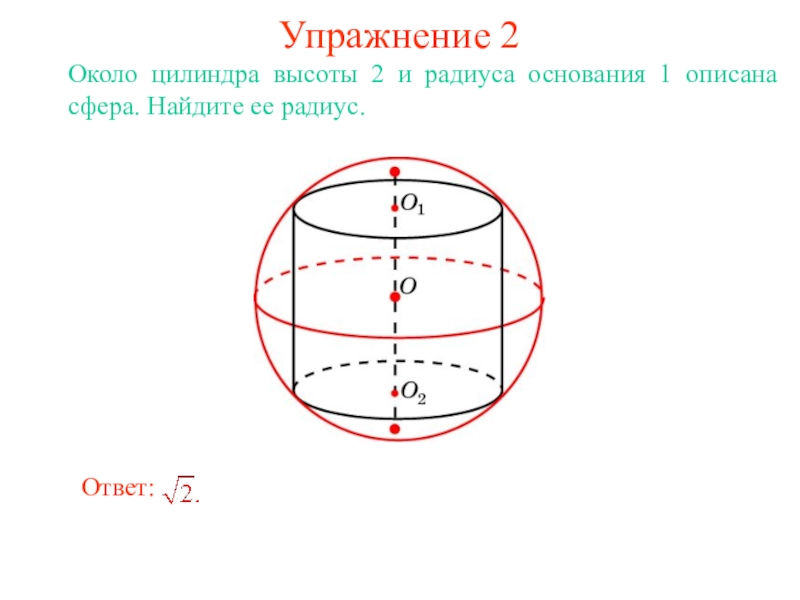
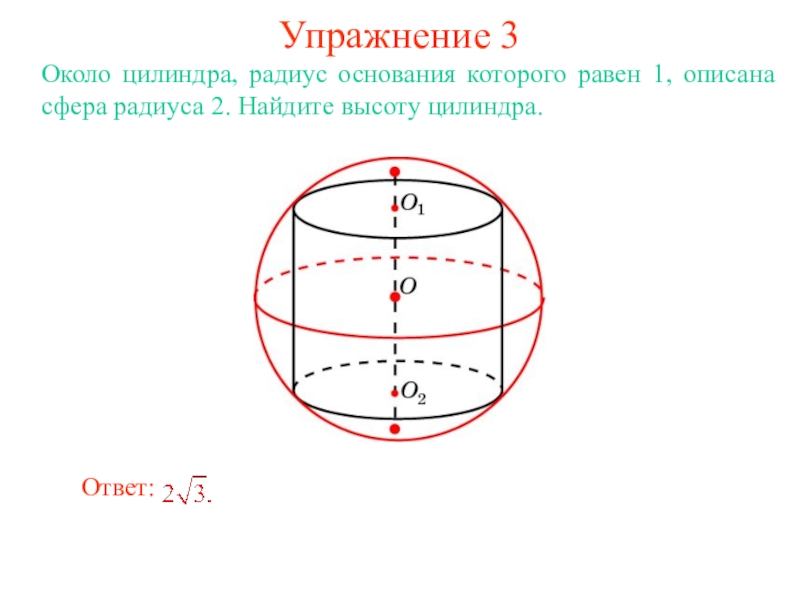
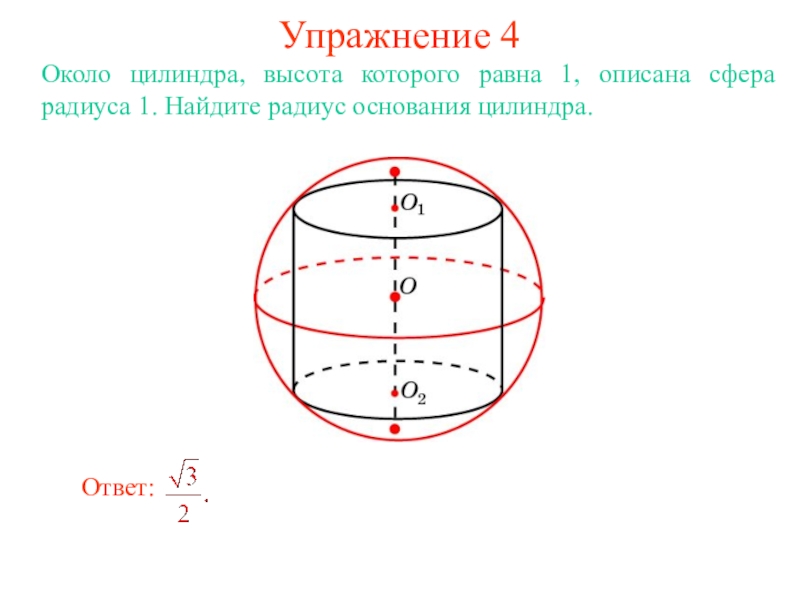
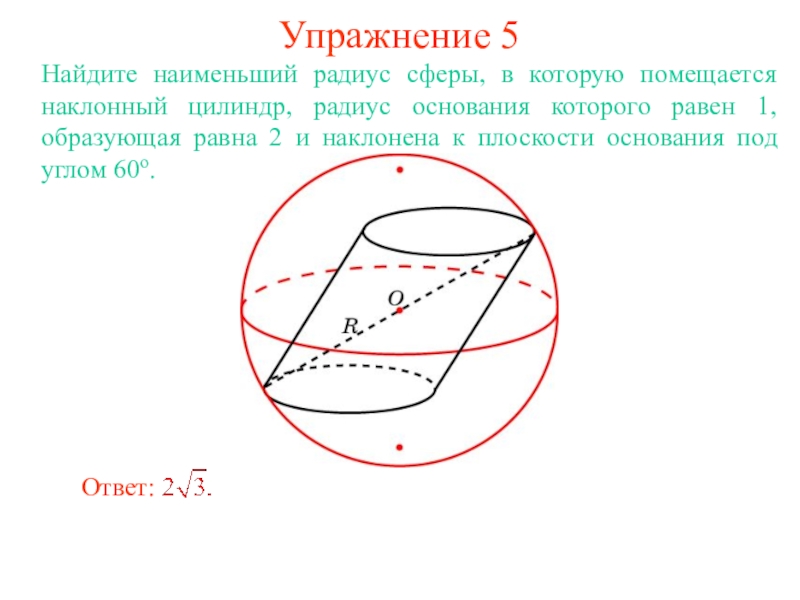
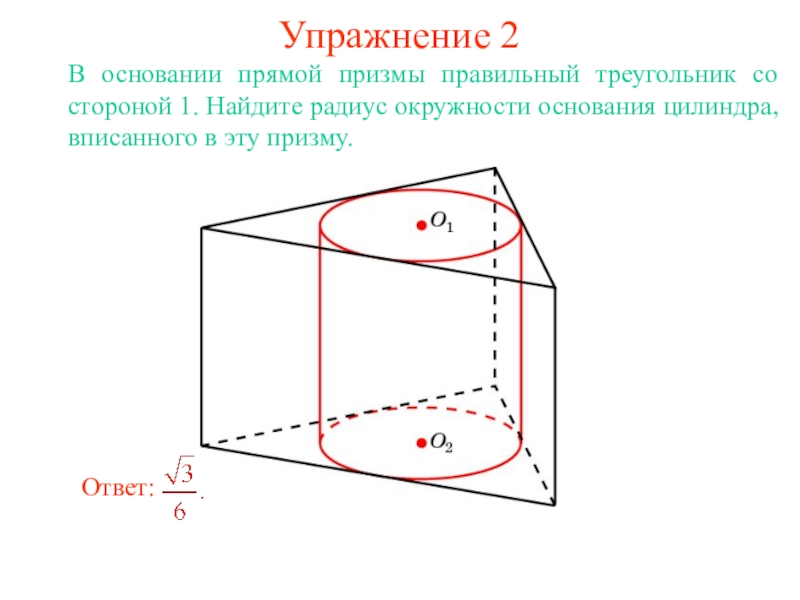
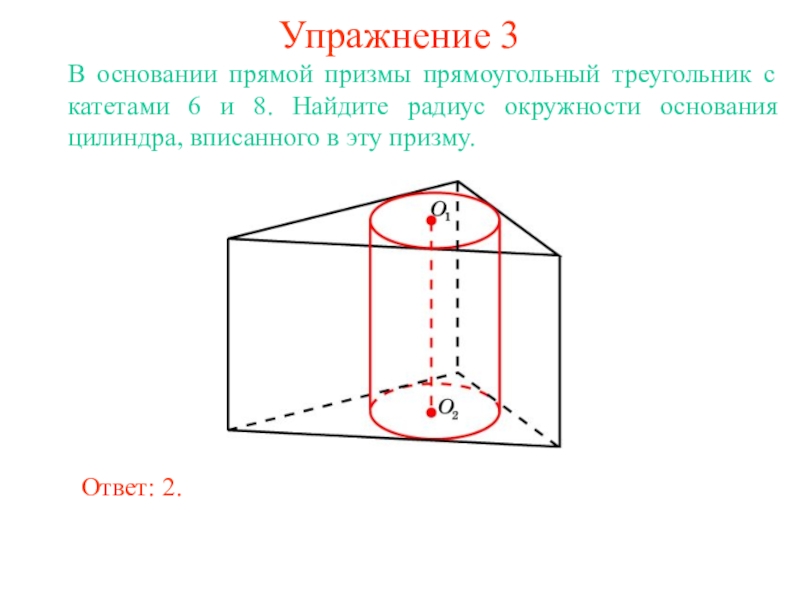
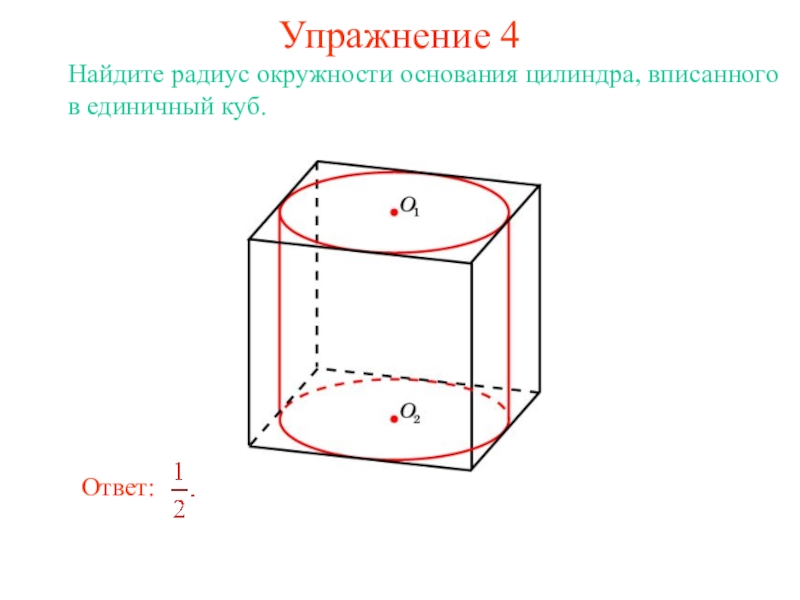
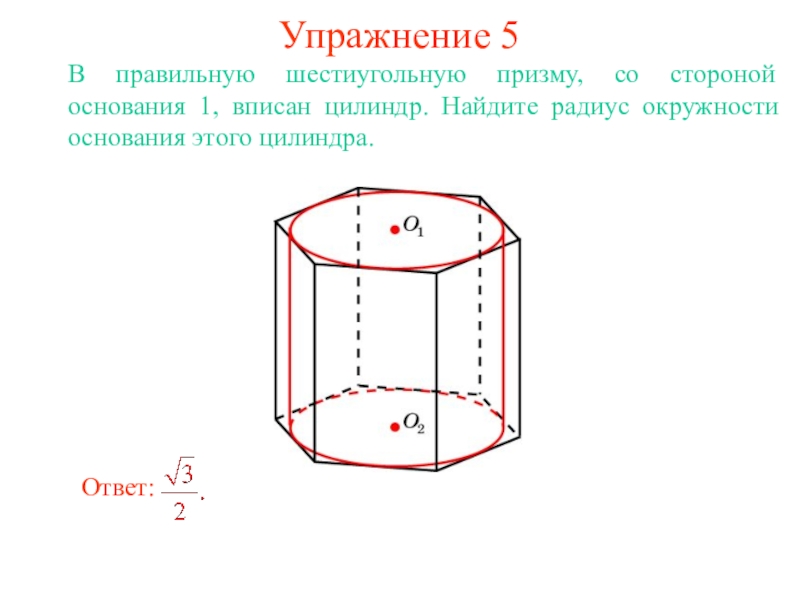
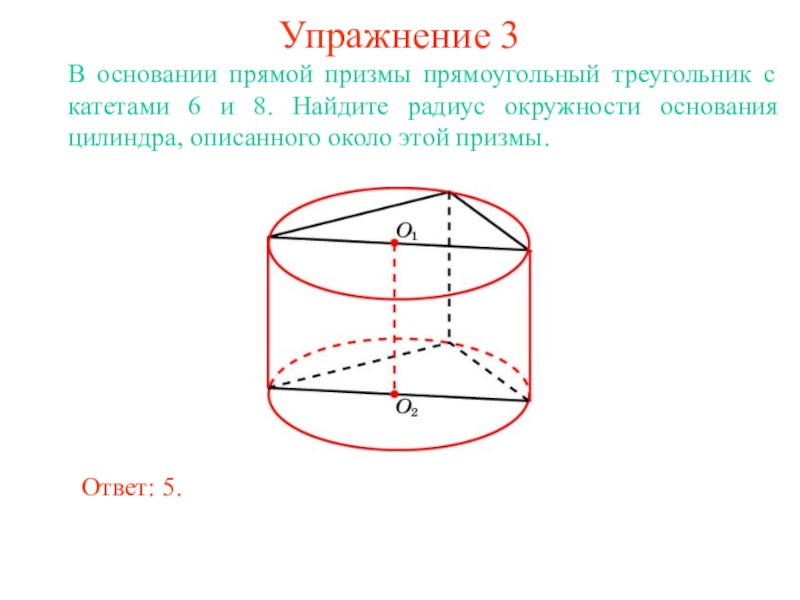
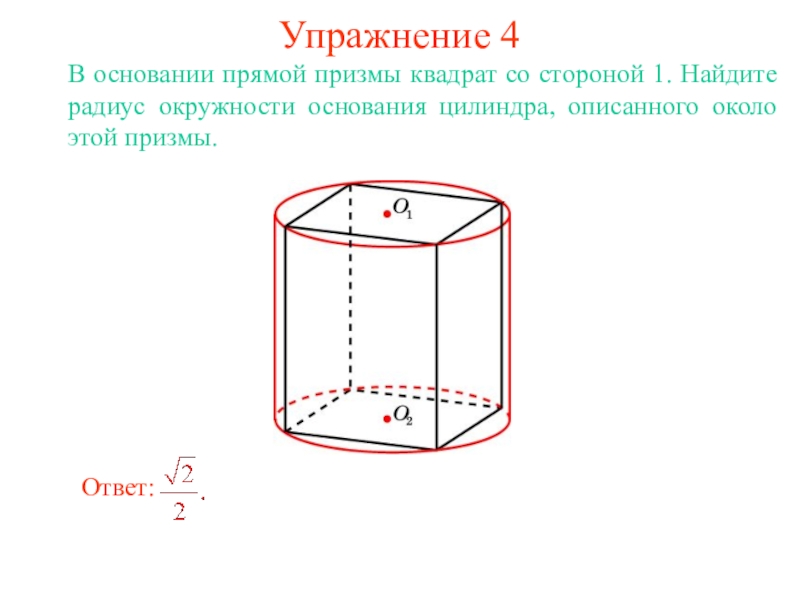
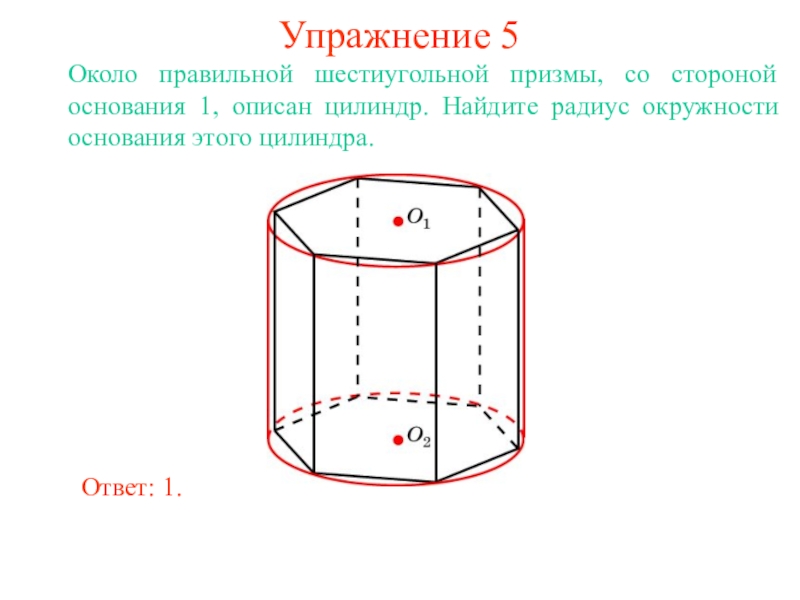
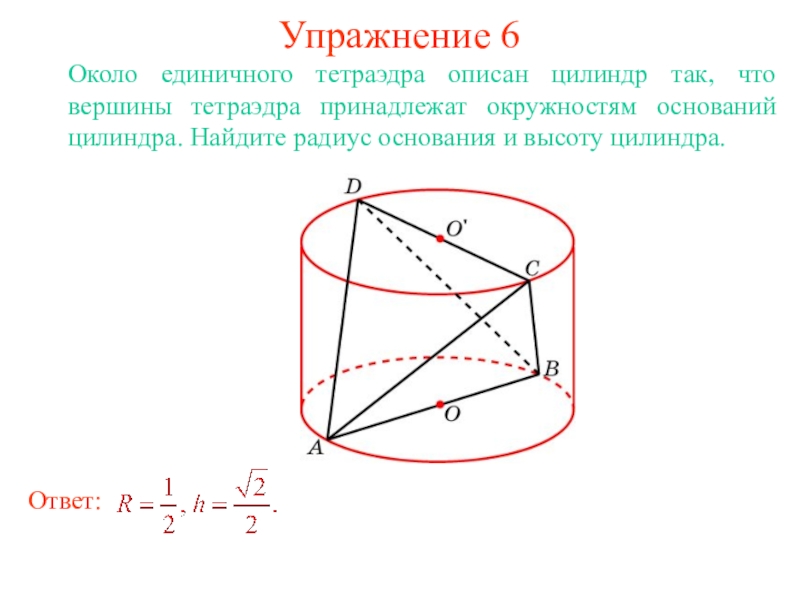
В цилиндр можно вписать сферу, если высота цилиндра равна

диаметру его основания.

Ее центром будет точка O, являющаяся

серединой отрезка, соединяющего центры оснований O1 и O2 цилиндра.

Радиус сферы R будет равен

радиусу окружности основания цилиндра.

Сфера, вписанная в цилиндрСфера называется вписанной в цилиндр, если она касается его оснований и боковой поверхности (касается

Слайд 2Упражнение 1
В цилиндр высоты 2 вписана сфера. Найдите ее радиус.
Ответ: 1.

Упражнение 1В цилиндр высоты 2 вписана сфера. Найдите ее радиус.Ответ: 1.

Слайд 3Упражнение 2
В цилиндр вписана сфера радиуса 1. Найдите высоту цилиндра.
Ответ: 2.

Упражнение 2В цилиндр вписана сфера радиуса 1. Найдите высоту цилиндра.Ответ: 2.

Слайд 4Упражнение 3
Радиус основания цилиндра равен 2. Какой должна быть высота цилиндра,

чтобы в него можно было вписать сферу?

Ответ: 4.

Упражнение 3Радиус основания цилиндра равен 2. Какой должна быть высота цилиндра, чтобы в него можно было вписать

Слайд 5Упражнение 4
Высота цилиндра равна 2. Каким должен быть радиус основания цилиндра,

чтобы в него можно было вписать сферу?

Ответ: 1.

Упражнение 4Высота цилиндра равна 2. Каким должен быть радиус основания цилиндра, чтобы в него можно было вписать

Слайд 6Упражнение 5
Осевым сечением цилиндра является прямоугольник со сторонами 1 и 2.

Можно ли в этот цилиндр вписать сферу?

Ответ: Нет.

Упражнение 5Осевым сечением цилиндра является прямоугольник со сторонами 1 и 2. Можно ли в этот цилиндр вписать

Слайд 7Упражнение 6
Осевым сечением цилиндра является квадрат. Можно ли в этот цилиндр

вписать сферу?

Ответ: Да.

Упражнение 6Осевым сечением цилиндра является квадрат. Можно ли в этот цилиндр вписать сферу?Ответ: Да.

Слайд 8Упражнение 7
Можно ли вписать сферу в цилиндр, осевым сечением которого является

ромб?

Ответ: Нет.

Упражнение 7Можно ли вписать сферу в цилиндр, осевым сечением которого является ромб?Ответ: Нет.

Слайд 9Упражнение 8
Можно ли вписать сферу в наклонный цилиндр?
Ответ: Нет.

Упражнение 8Можно ли вписать сферу в наклонный цилиндр?Ответ: Нет.

Слайд 10Упражнение 9
Площадь осевого сечения цилиндра, в который вписана сфера, равна 4

см2. Найдите диаметр сферы.

Ответ: 2 см.

Упражнение 9Площадь осевого сечения цилиндра, в который вписана сфера, равна 4 см2. Найдите диаметр сферы.Ответ: 2 см.

Слайд 11Упражнение 10
Периметр осевого сечения цилиндра, в который вписана сфера, равен 8

см. Найдите радиус сферы.

Ответ: 1 см.

Упражнение 10Периметр осевого сечения цилиндра, в который вписана сфера, равен 8 см. Найдите радиус сферы.Ответ: 1 см.

Слайд 12Упражнение 11
Какой наибольший радиус может быть у сферы, помещающейся в цилиндр,

радиус основания которого равен 2, и высота 1.

Ответ: 0,5 см.

Упражнение 11Какой наибольший радиус может быть у сферы, помещающейся в цилиндр, радиус основания которого равен 2, и

Слайд 13Упражнение 12
Можно ли сферу радиуса 1 поместить в наклонный цилиндр, радиус

основания которого равен 1, а боковое ребро равно 2 и наклонено к плоскости основания под углом 60о.

Ответ: Нет.

Упражнение 12Можно ли сферу радиуса 1 поместить в наклонный цилиндр, радиус основания которого равен 1, а боковое

Слайд 14Упражнение 13
Какой наибольший радиус может быть у сферы, помещающейся в наклонный

цилиндр, радиус основания которого равен 1, а боковое ребро равно 2 и наклонено к плоскости основания под углом 60о.
Упражнение 13Какой наибольший радиус может быть у сферы, помещающейся в наклонный цилиндр, радиус основания которого равен 1,

Слайд 15Сфера, описанная около цилиндра
Цилиндр называется вписанным в сферу, если окружности оснований

цилиндра лежат на сфере. При этом сфера называется описанной около цилиндра.
Сфера, описанная около цилиндраЦилиндр называется вписанным в сферу, если окружности оснований цилиндра лежат на сфере. При этом

Слайд 16Упражнение 1
Диагональ осевого сечения цилиндра равна 2. Найдите радиус сферы, описанной

около этого цилиндра.

Ответ: 1.

Упражнение 1Диагональ осевого сечения цилиндра равна 2. Найдите радиус сферы, описанной около этого цилиндра.Ответ: 1.

Слайд 17Упражнение 2
Около цилиндра высоты 2 и радиуса основания 1 описана сфера.

Найдите ее радиус.
Упражнение 2Около цилиндра высоты 2 и радиуса основания 1 описана сфера. Найдите ее радиус.

Слайд 18Упражнение 3
Около цилиндра, радиус основания которого равен 1, описана сфера радиуса

2. Найдите высоту цилиндра.
Упражнение 3Около цилиндра, радиус основания которого равен 1, описана сфера радиуса 2. Найдите высоту цилиндра.

Слайд 19Упражнение 4
Около цилиндра, высота которого равна 1, описана сфера радиуса 1.

Найдите радиус основания цилиндра.
Упражнение 4Около цилиндра, высота которого равна 1, описана сфера радиуса 1. Найдите радиус основания цилиндра.

Слайд 20Упражнение 5
Найдите наименьший радиус сферы, в которую помещается наклонный цилиндр, радиус

основания которого равен 1, образующая равна 2 и наклонена к плоскости основания под углом 60о.
Упражнение 5Найдите наименьший радиус сферы, в которую помещается наклонный цилиндр, радиус основания которого равен 1, образующая равна

Слайд 21Цилиндр, вписанный в призму
Цилиндр называется вписанным в призму, если его основания

вписаны в основания цилиндра. При этом, призма называется описанной около цилиндра

В призму можно вписать цилиндр тогда и только тогда, когда

в ее основание можно вписать окружность.

Радиус основания цилиндра равен

радиусу окружности, вписанной в основание призмы.

Высота цилиндра равна

высоте призмы.

Цилиндр, вписанный в призмуЦилиндр называется вписанным в призму, если его основания вписаны в основания цилиндра. При этом,

Слайд 22Упражнение 1
Можно ли вписать цилиндр в наклонную призму?
Ответ: Да, наклонный цилиндр.

Упражнение 1Можно ли вписать цилиндр в наклонную призму?Ответ: Да, наклонный цилиндр.

Слайд 23Упражнение 2
В основании прямой призмы правильный треугольник со стороной 1. Найдите

радиус окружности основания цилиндра, вписанного в эту призму.
Упражнение 2В основании прямой призмы правильный треугольник со стороной 1. Найдите радиус окружности основания цилиндра, вписанного в

Слайд 24Упражнение 3
В основании прямой призмы прямоугольный треугольник с катетами 6 и

8. Найдите радиус окружности основания цилиндра, вписанного в эту призму.

Ответ: 2.

Упражнение 3В основании прямой призмы прямоугольный треугольник с катетами 6 и 8. Найдите радиус окружности основания цилиндра,

Слайд 25Упражнение 4
Найдите радиус окружности основания цилиндра, вписанного в единичный куб.

Упражнение 4Найдите радиус окружности основания цилиндра, вписанного в единичный куб.

Слайд 26Упражнение 5
В правильную шестиугольную призму, со стороной основания 1, вписан цилиндр.

Найдите радиус окружности основания этого цилиндра.
Упражнение 5В правильную шестиугольную призму, со стороной основания 1, вписан цилиндр. Найдите радиус окружности основания этого цилиндра.

Слайд 27Цилиндр, описанный около призмы
Цилиндр называется описанным около призмы, если его основания

описаны около оснований цилиндра. При этом, призма называется вписанной в цилиндр

Около призмы можно описать цилиндр, если около ее оснований можно описать окружности.

Высота цилиндра равна

высоте призмы.

радиусу окружности, описанной около основания призмы.

Радиус основания цилиндра равен

Цилиндр, описанный около призмыЦилиндр называется описанным около призмы, если его основания описаны около оснований цилиндра. При этом,

Слайд 28Упражнение 1
Можно ли описать цилиндр около наклонной призмы?
Ответ: Да, наклонный цилиндр.

Упражнение 1Можно ли описать цилиндр около наклонной призмы?Ответ: Да, наклонный цилиндр.

Слайд 29Упражнение 2
В основании прямой призмы правильный треугольник со стороной 1. Найдите

радиус окружности основания цилиндра, описанного около этой призмы.
Упражнение 2В основании прямой призмы правильный треугольник со стороной 1. Найдите радиус окружности основания цилиндра, описанного около

Слайд 30Упражнение 3
В основании прямой призмы прямоугольный треугольник с катетами 6 и

8. Найдите радиус окружности основания цилиндра, описанного около этой призмы.

Ответ: 5.

Упражнение 3В основании прямой призмы прямоугольный треугольник с катетами 6 и 8. Найдите радиус окружности основания цилиндра,

Слайд 31Упражнение 4
В основании прямой призмы квадрат со стороной 1. Найдите радиус

окружности основания цилиндра, описанного около этой призмы.
Упражнение 4В основании прямой призмы квадрат со стороной 1. Найдите радиус окружности основания цилиндра, описанного около этой

Слайд 32Упражнение 5
Около правильной шестиугольной призмы, со стороной основания 1, описан цилиндр.

Найдите радиус окружности основания этого цилиндра.

Ответ: 1.

Упражнение 5Около правильной шестиугольной призмы, со стороной основания 1, описан цилиндр. Найдите радиус окружности основания этого цилиндра.Ответ:

Слайд 33Упражнение 6
Около единичного тетраэдра описан цилиндр так, что вершины тетраэдра принадлежат

окружностям оснований цилиндра. Найдите радиус основания и высоту цилиндра.
Упражнение 6Около единичного тетраэдра описан цилиндр так, что вершины тетраэдра принадлежат окружностям оснований цилиндра. Найдите радиус основания

Слайд 34Упражнение 7
Около единичного октаэдра описан цилиндр так, что две противоположные вершины

октаэдра находятся в центрах оснований цилиндра, а остальные вершины принадлежат боковой поверхности цилиндра. Найдите радиус основания и высоту цилиндра.
Упражнение 7Около единичного октаэдра описан цилиндр так, что две противоположные вершины октаэдра находятся в центрах оснований цилиндра,
Скачать презентацию

Похожие презентации

Центральные и вписанные углы геометрия 8 класс Центральные и вписанные углы геометрия 8 класс 268
Презентация по теме Пифагор и его школа ученицы 8 класса Рябовой Марины Презентация по теме Пифагор и его школа ученицы 8 класса Рябовой Марины 208
Презентация по математике: Параллельность прямых и плоскостей Презентация по математике: Параллельность прямых и плоскостей 239
Презентация к уроку по геометрии на тему Симметрия (8 класс) Презентация к уроку по геометрии на тему Симметрия (8 класс) 415
Презентация к уроку Практическое применение теоремы Пифагора Презентация к уроку Практическое применение теоремы Пифагора 194
Гл.2. Урок 11. Теорема, обратная теореме Пифагора Гл.2. Урок 11. Теорема, обратная теореме Пифагора 206

Что такое shareslide.ru?

Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.

Для правообладателей

Яндекс.Метрика

Обратная связь

Email: Нажмите что бы посмотреть