- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Векторы в пространстве
Содержание
- 1. Презентация по геометрии Векторы в пространстве
- 2. Основные определения и обозначения для векторов в
- 3. Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор.Абсолютная величина вектора
- 4. Векторы с равными модулями и одинаковыми направлениями
- 5. Так же, как и на плоскости, координатами
- 6. На рисунках направление вектора обозначается стрелкой от
- 7. Два ненулевых вектора называются коллинеарными, если они лежат на
Основные определения и обозначения для векторов в пространстве вводятся так же, как и для векторов на плоскости. Вектор – направленный отрезок. Другими словами, вектором называется отрезок, для которого указано, какой из его концов является началом, а какой концом.
Слайд 2Основные определения и обозначения для векторов в пространстве вводятся так же,
как и для векторов на плоскости.
Вектор – направленный отрезок. Другими словами, вектором называется отрезок, для которого указано, какой из его концов является началом, а какой концом.
Вектор характеризуется следующими элементами:
1) начальной точкой (точкой приложения); 2) направлением; 3) длиной («модулем вектора», абсолютной величиной).
Величины, которые характеризуются, не только числом, но еще и направлением, называются векторными величинами или просто векторами. Векторами являются, например, скорость, ускорение, сила.
Вектор – направленный отрезок. Другими словами, вектором называется отрезок, для которого указано, какой из его концов является началом, а какой концом.
Вектор характеризуется следующими элементами:
1) начальной точкой (точкой приложения); 2) направлением; 3) длиной («модулем вектора», абсолютной величиной).
Величины, которые характеризуются, не только числом, но еще и направлением, называются векторными величинами или просто векторами. Векторами являются, например, скорость, ускорение, сила.
Слайд 3Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор.
Абсолютная величина вектора а обозначается как а
.
Два вектора называются равными, если они совмещаются параллельным переносом.
От любой точки можно отложить вектор, равный данному, и притом только один, используя параллельный перенос.
АВСD — параллелограмм, AB = CD
Два вектора называются равными, если они совмещаются параллельным переносом.
От любой точки можно отложить вектор, равный данному, и притом только один, используя параллельный перенос.
АВСD — параллелограмм, AB = CD
Слайд 4Векторы с равными модулями и одинаковыми направлениями также равными векторами.
Векторы с
равными модулями и противоположными направлениями называются противоположными векторами.
Меняя направление какого-либо вектора на противоположное, получается вектор, противоположный данному: AB = −BA.
Меняя направление какого-либо вектора на противоположное, получается вектор, противоположный данному: AB = −BA.
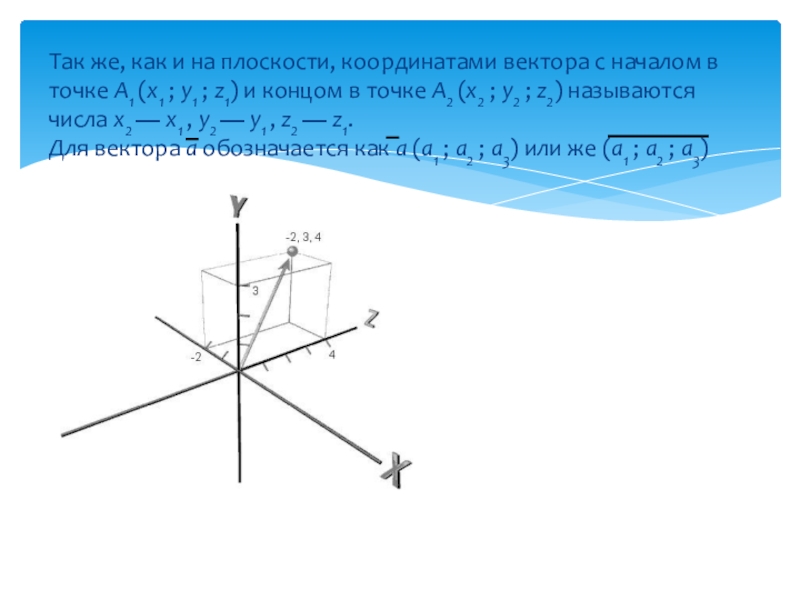
Слайд 5Так же, как и на плоскости, координатами вектора с началом в
точке A1 (x1 ; y1 ; z1) и концом в точке A2 (x2 ; y2 ; z2) называются числа x2 — x1 , y2 — y1 , z2 — z1.
Для вектора a обозначается как a (a1 ; a2 ; a3) или же (a1 ; a2 ; a3)
Слайд 6На рисунках направление вектора обозначается стрелкой от начала к концу. Если
длина рассматриваемого отрезка равна нулю, то есть отрезок вырождается в точку, то эта точка тоже может рассматриваться как вектор. Такой вектор называется нулевым и имеет произвольное направление.
Нулевой вектор — точка в пространстве. Начало и конец нулевого вектора совпадают, и он не имеет длины и направления.
Иногда обозначается как 0.
С нулевым вектором не связывают никакого направления в пространстве. Можно считать, что нулевой вектор одновременно параллелен и перпендикулярен любому вектору пространства (легко выводится из определения).
Нулевой вектор — точка в пространстве. Начало и конец нулевого вектора совпадают, и он не имеет длины и направления.
Иногда обозначается как 0.
С нулевым вектором не связывают никакого направления в пространстве. Можно считать, что нулевой вектор одновременно параллелен и перпендикулярен любому вектору пространства (легко выводится из определения).
Слайд 7Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на
параллельных прямых.
Если векторы а и b коллинеарны и их лучи сонаправлены, то эти векторы называются сонаправленными.
Обозначаются как а b .
Если векторы a и b коллинеарны, а их лучи не являются сонаправленными, то эти векторы называются противоположно направленными.
Обозначаются как a b .
Нулевой вектор условились считать сонаправленным с любым вектором.
Если векторы а и b коллинеарны и их лучи сонаправлены, то эти векторы называются сонаправленными.
Обозначаются как а b .
Если векторы a и b коллинеарны, а их лучи не являются сонаправленными, то эти векторы называются противоположно направленными.
Обозначаются как a b .
Нулевой вектор условились считать сонаправленным с любым вектором.