математики
первой квалификационной категории
Маврина Т.В.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Векторы в пространстве ( 11 класс)
Содержание
- 1. Презентация по геометрии Векторы в пространстве ( 11 класс)
- 2. Понятиевекторав пространствеУчитель математики МКОУ "Хотьковская СОШ" Коломина Н.Н.
- 3. Дано:АВСD – тетраэдр,Точки М,N,K – середины рёбер
- 4. № 323АВСDМNPQДано:АВСD – тетраэдр, рёбра которого равны.Точки
- 5. № 326АВСDА'В'С'D'МKДано:АВСDА'В'С'D' – параллелепипед.Точки М и К
- 6. Сложение и вычитаниевекторов.Умножение векторана число.Учитель математики МКОУ "Хотьковская СОШ" Коломина Н.Н.
- 7. АВСDА'В'С'D'МKДано:АВСDА'В'С'D' – параллелепипед.Точки М и К –
- 8. KLMNK'L'M'N'№ 334Дано:KLMNK‘L‘M‘N' – прямоугольный параллелепипед.Докажите, что:а) |MK+MM'
- 9. AB1BC1CD1DA1OДано:ABCDA1B1C1D1 – куб.B1D ∩ C1A = т.
- 10. Компланарныевекторы.Учитель математики МКОУ "Хотьковская СОШ" Коломина Н.Н.
- 11. ABCDOMДано:OABCD – пирамида.ABCD – параллелограмм.BD ∩ CA
- 12. AB1BC1CD1DA1O№ 368MNДано:ABCDA1B1C1D1 – прямоугольный параллелепипед.т.М и т.N
- 13. MNPQM1N1P1Q1Дано:MNPQM1N1P1Q1 –параллелепипед.Докажите, что:а) MQ + M1Q1 =
- 14. АBDCFEДано:ABCDEF –правильный октаэдр.Докажите, что:а) АВ + FB
Понятиевекторав пространствеУчитель математики МКОУ "Хотьковская СОШ" Коломина Н.Н.
Слайд 1Векторы в пространстве
Решение задач по готовым чертежам.
Урок геометрии в 11 классе.
Подготовила
учитель
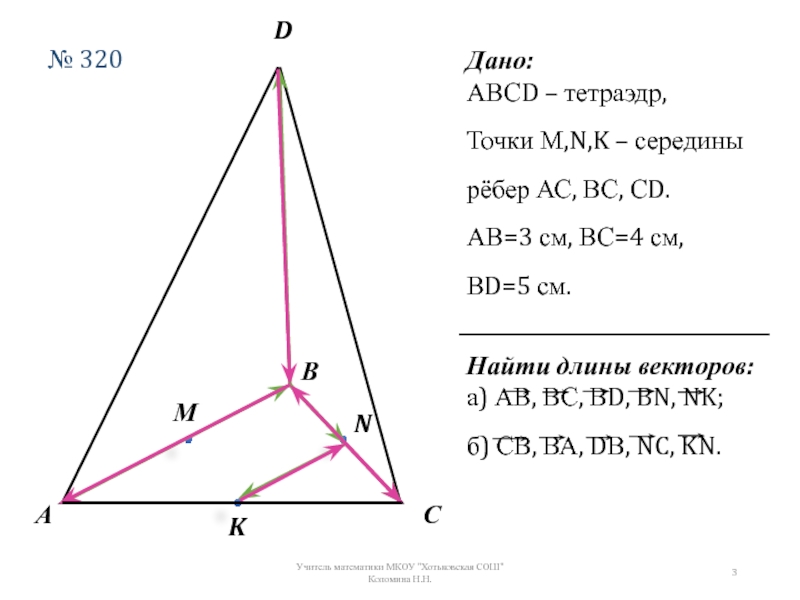
Слайд 3Дано:
АВСD – тетраэдр,
Точки М,N,K – середины рёбер АС, ВС, СD.
АВ=3 см,
ВС=4 см,
ВD=5 см.
Найти длины векторов:
а) АВ, ВС, ВD, BN, NK;
б) СВ, ВА, DВ, NC, KN.
ВD=5 см.
Найти длины векторов:
а) АВ, ВС, ВD, BN, NK;
б) СВ, ВА, DВ, NC, KN.
А
В
С
D
М
N
K
№ 320
Учитель математики МКОУ "Хотьковская СОШ" Коломина Н.Н.
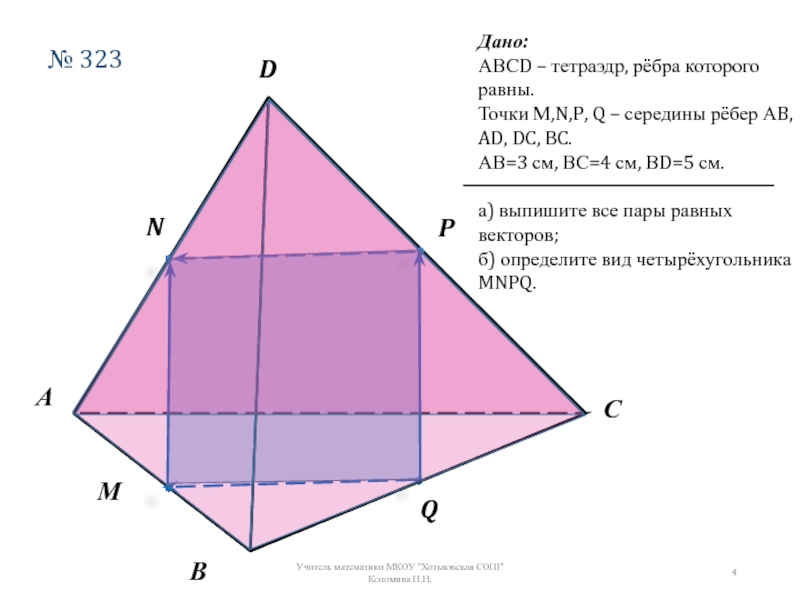
Слайд 4№ 323
А
В
С
D
М
N
P
Q
Дано:
АВСD – тетраэдр, рёбра которого равны.
Точки М,N,P, Q – середины
рёбер АB, AD, DC, BC.
АВ=3 см, ВС=4 см, ВD=5 см.
а) выпишите все пары равных векторов;
б) определите вид четырёхугольника MNPQ.
АВ=3 см, ВС=4 см, ВD=5 см.
а) выпишите все пары равных векторов;
б) определите вид четырёхугольника MNPQ.
Учитель математики МКОУ "Хотьковская СОШ" Коломина Н.Н.
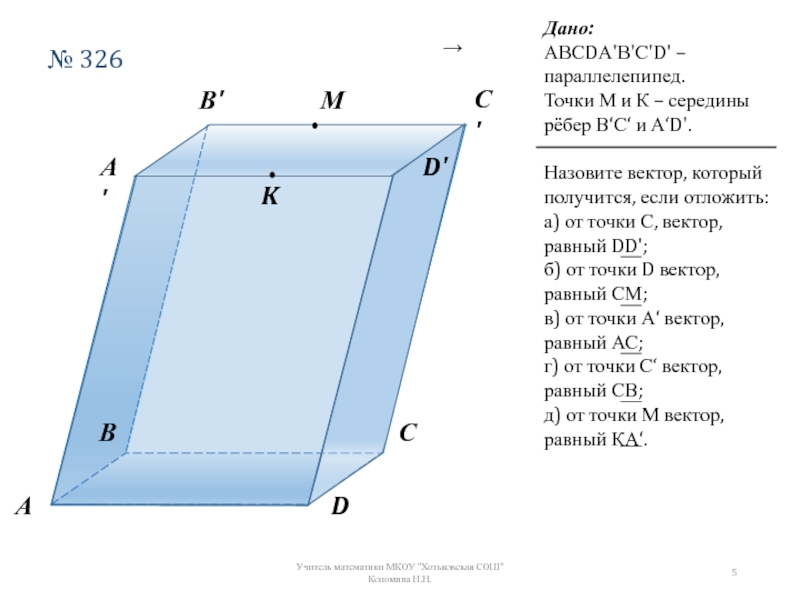
Слайд 5№ 326
А
В
С
D
А'
В'
С'
D'
М
K
Дано:
АВСDА'В'С'D' – параллелепипед.
Точки М и К – середины рёбер ‘ё
и А‘D'.
Назовите вектор, который получится, если отложить:
а) от точки С, вектор, равный DD';
б) от точки D вектор, равный СМ;
в) от точки А‘ вектор, равный АС;
г) от точки С‘ вектор, равный СВ;
д) от точки М вектор, равный КА‘.
Назовите вектор, который получится, если отложить:
а) от точки С, вектор, равный DD';
б) от точки D вектор, равный СМ;
в) от точки А‘ вектор, равный АС;
г) от точки С‘ вектор, равный СВ;
д) от точки М вектор, равный КА‘.
Учитель математики МКОУ "Хотьковская СОШ" Коломина Н.Н.
→
Слайд 6Сложение и вычитание
векторов.
Умножение вектора
на число.
Учитель математики МКОУ "Хотьковская СОШ" Коломина Н.Н.
Слайд 7А
В
С
D
А'
В'
С'
D'
М
K
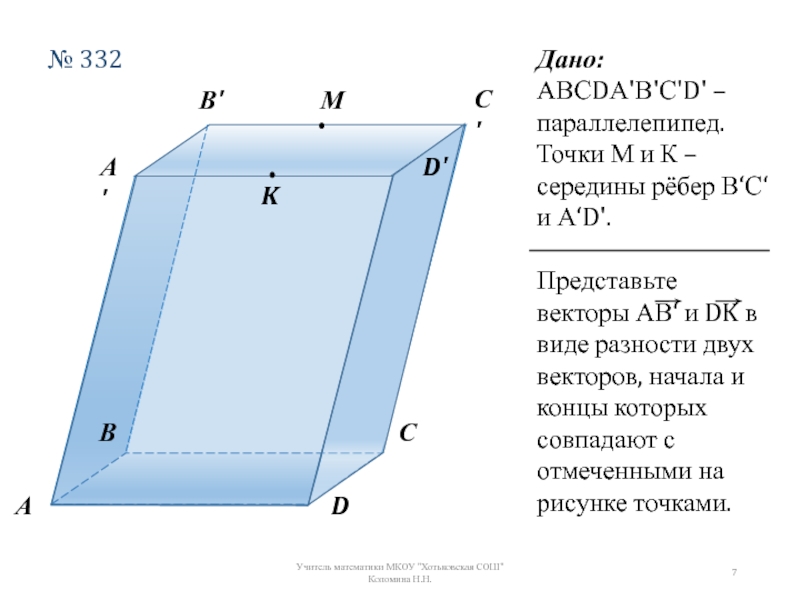
Дано:
АВСDА'В'С'D' – параллелепипед.
Точки М и К – середины рёбер ‘ё и
А‘D'.
Представьте векторы АВ‘ и DK в виде разности двух векторов, начала и концы которых совпадают с отмеченными на рисунке точками.
Представьте векторы АВ‘ и DK в виде разности двух векторов, начала и концы которых совпадают с отмеченными на рисунке точками.
№ 332
Учитель математики МКОУ "Хотьковская СОШ" Коломина Н.Н.
Слайд 8K
L
M
N
K'
L'
M'
N'
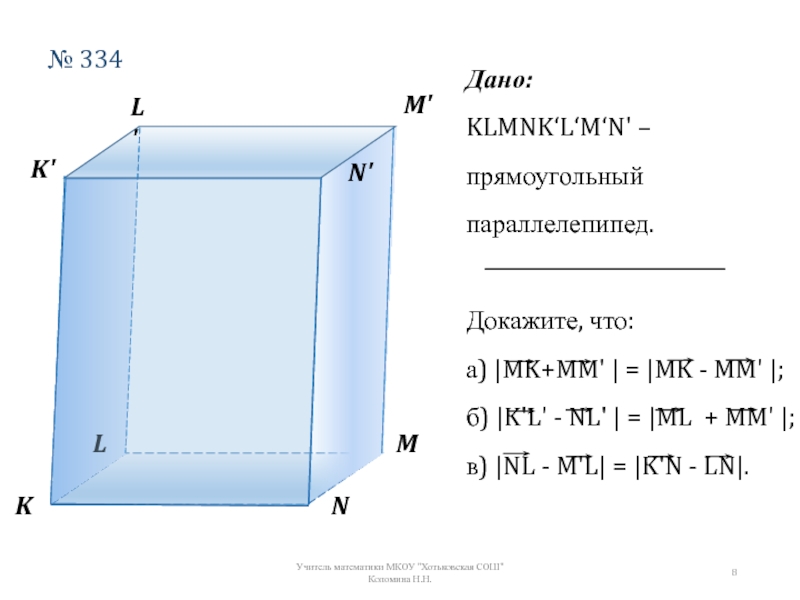
№ 334
Дано:
KLMNK‘L‘M‘N' – прямоугольный параллелепипед.
Докажите, что:
а) |MK+MM' | = |MK -
MM' |;
б) |K'L' - NL' | = |ML + MM' |;
в) |NL - M'L| = |K'N - LN|.
б) |K'L' - NL' | = |ML + MM' |;
в) |NL - M'L| = |K'N - LN|.
Учитель математики МКОУ "Хотьковская СОШ" Коломина Н.Н.
Слайд 9A
B1
B
C1
C
D1
D
A1
O
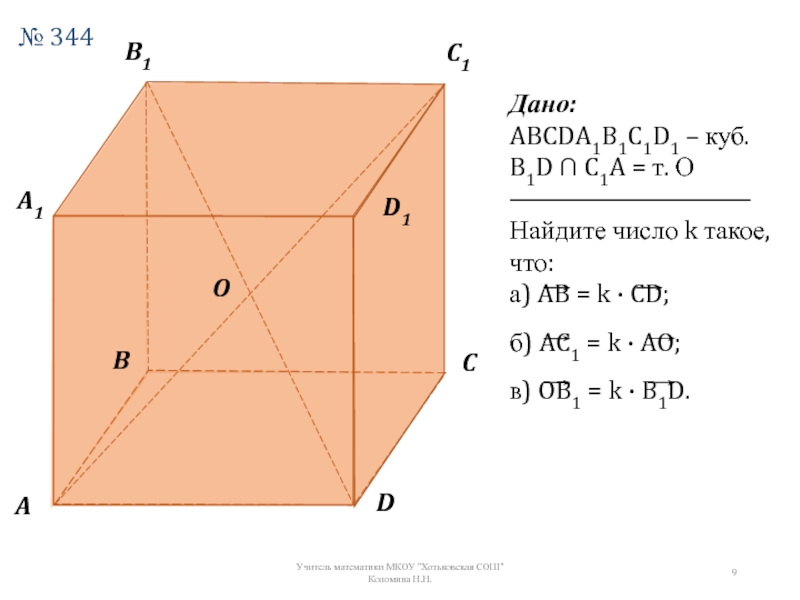
Дано:
ABCDA1B1C1D1 – куб.
B1D ∩ C1A = т. О
Найдите число k такое,
что:
а) AB = k · CD;
б) AC1 = k · AO;
в) OB1 = k · B1D.
а) AB = k · CD;
б) AC1 = k · AO;
в) OB1 = k · B1D.
№ 344
Учитель математики МКОУ "Хотьковская СОШ" Коломина Н.Н.
Слайд 11A
B
C
D
O
M
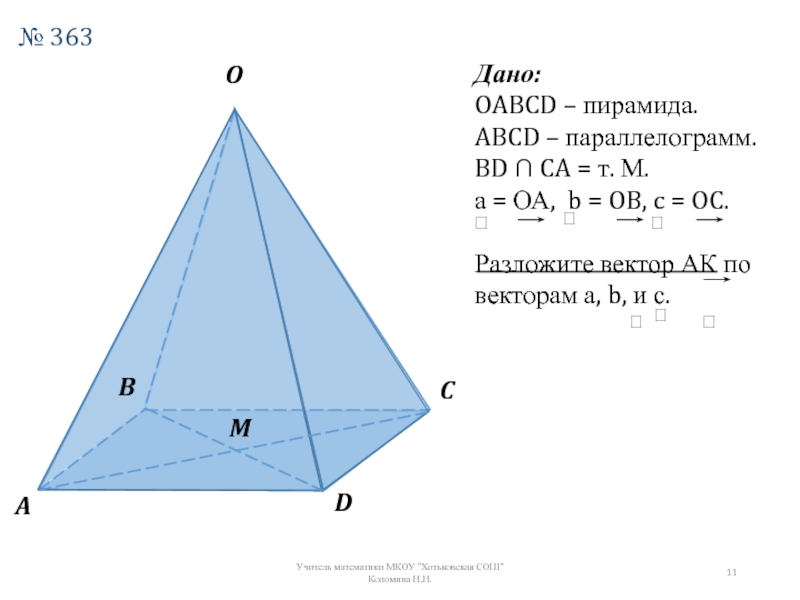
Дано:
OABCD – пирамида.
ABCD – параллелограмм.
BD ∩ CA = т. М.
а =
ОА, b = OB, c = OC.
Разложите вектор АК по векторам а, b, и с.
Разложите вектор АК по векторам а, b, и с.
№ 363
Учитель математики МКОУ "Хотьковская СОШ" Коломина Н.Н.
Слайд 12A
B1
B
C1
C
D1
D
A1
O
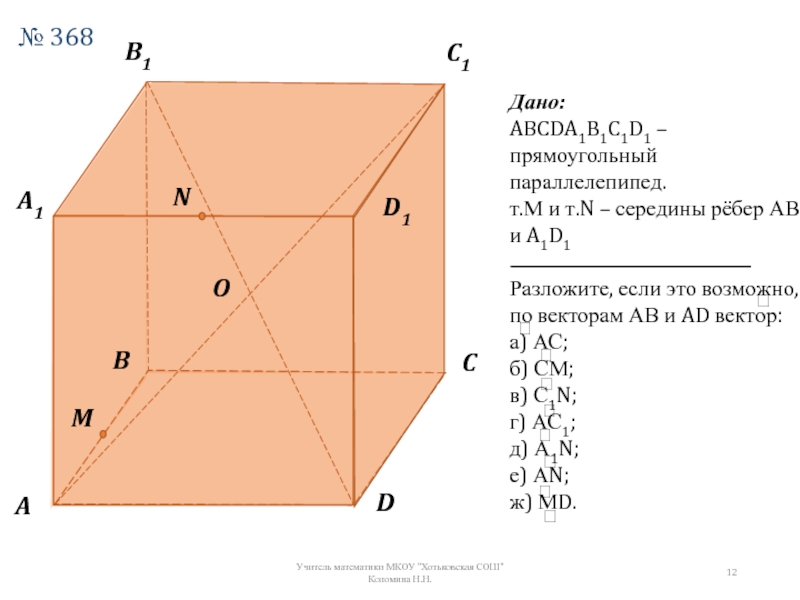
№ 368
M
N
Дано:
ABCDA1B1C1D1 – прямоугольный параллелепипед.
т.М и т.N – середины рёбер АВ
и A1D1
Разложите, если это возможно, по векторам АВ и AD вектор:
а) АС;
б) СМ;
в) С1N;
г) АС1;
д) А1N;
е) АN;
ж) МD.
Разложите, если это возможно, по векторам АВ и AD вектор:
а) АС;
б) СМ;
в) С1N;
г) АС1;
д) А1N;
е) АN;
ж) МD.
Учитель математики МКОУ "Хотьковская СОШ" Коломина Н.Н.
Слайд 13M
N
P
Q
M1
N1
P1
Q1
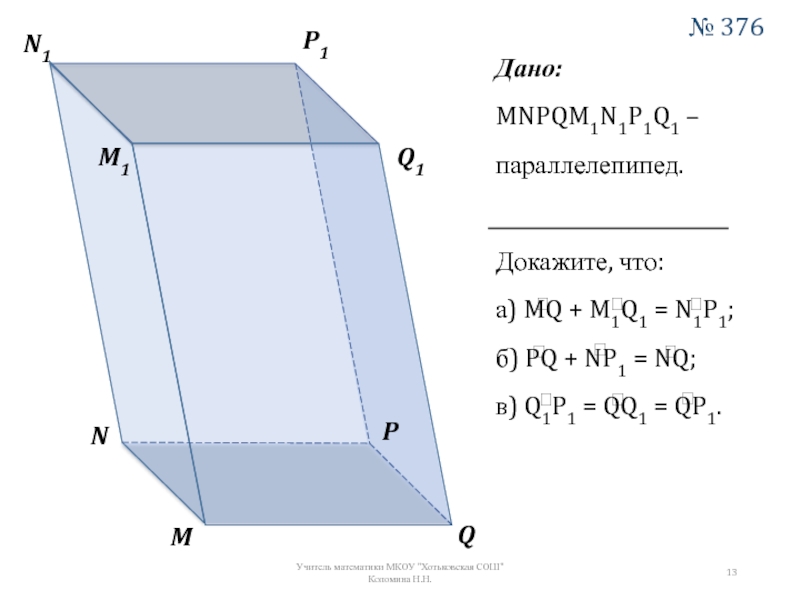
Дано:
MNPQM1N1P1Q1 –параллелепипед.
Докажите, что:
а) MQ + M1Q1 = N1P1;
б) PQ + NP1
= NQ;
в) Q1P1 = QQ1 = QP1.
в) Q1P1 = QQ1 = QP1.
№ 376
Учитель математики МКОУ "Хотьковская СОШ" Коломина Н.Н.
Слайд 14А
B
D
C
F
E
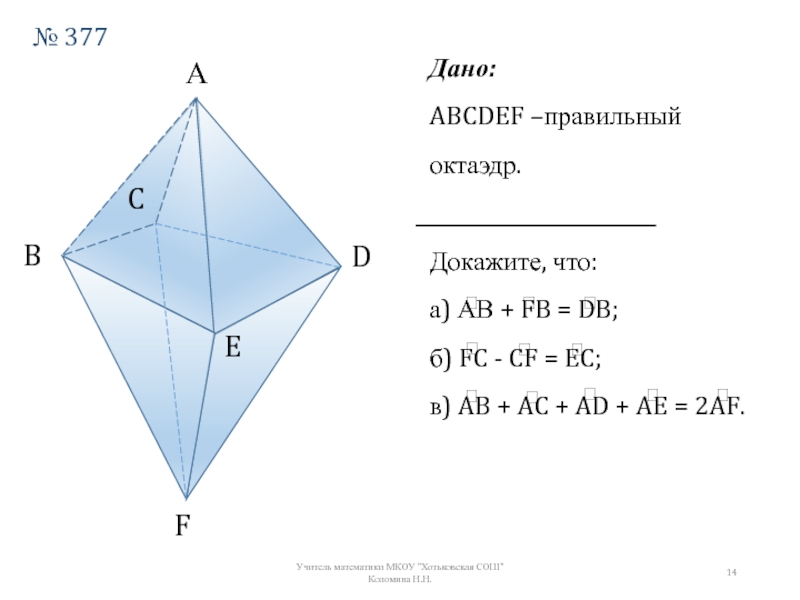
Дано:
ABCDEF –правильный октаэдр.
Докажите, что:
а) АВ + FB = DB;
б) FC -
CF = EC;
в) AB + AC + AD + AE = 2AF.
в) AB + AC + AD + AE = 2AF.
№ 377
Учитель математики МКОУ "Хотьковская СОШ" Коломина Н.Н.
