- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии в 7 классе на тему Треугольники. Применение треугольников в практической жизни.
Содержание
- 1. Презентация по геометрии в 7 классе на тему Треугольники. Применение треугольников в практической жизни.
- 2. Это треугольники
- 3. ОпределениеТреугольник – это фигура, которая состоит из
- 4. Виды треугольников по сторонамТреугольникиРавнобедренныйРавностороннийРазносторонний
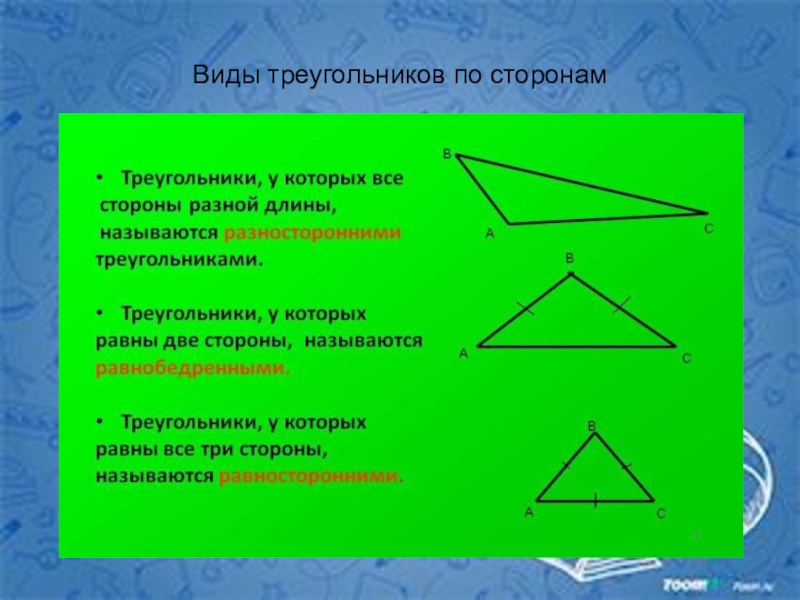
- 5. Виды треугольников по сторонам
- 6. Виды треугольников по угламТреугольникиПрямоугольныйОстроугольныйТупоугольный
- 7. Виды треугольников по угламОстроугольный – у него
- 8. Историческая справкаТреугольник – самая простая замкнутая прямолинейная
- 9. Практическое применение треугольников Равнобедренные треугольники
- 10. Геометрическая фигура «Флексагон» (от англ. to flex,
- 11. Египетский треугольник. Землемеры Древнего Египта для построения
- 12. Слайд 12
- 13. Тайны пирамиды ХеопсаПирамиды «умеют» очень многое. Растворимый
- 14. Где же можно встретить треугольники, кроме математики?Начиная
- 15. Правило «золотого треугольника»Правило «золотого треугольника» основано на
- 16. Бермудский треугольникБермудский треугольник иногда еще называют дьявольским
- 17. Из третьего признака равенства треугольников следует, что
- 18. Это свойство – жесткость треугольника – широко
- 19. Треугольники в конструкции железнодорожного моста.
- 20. В глубокой древности вместе с астрономией появилась
- 21. Треугольник ПаскаляУстройство треугольника Паскаля: каждое число равно
- 22. Треугольник Пенроуза или трибар из коллекции невозможных
- 23. Спасибо за внимание!
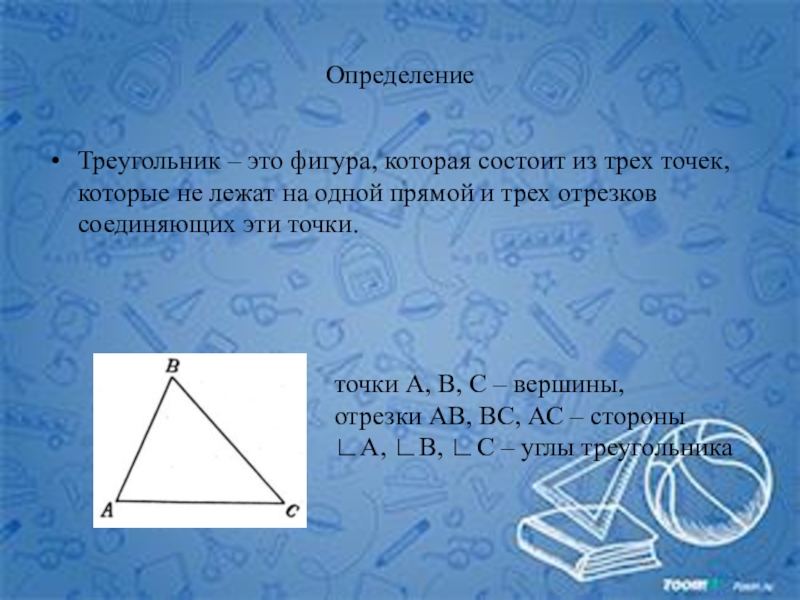
Слайд 3Определение
Треугольник – это фигура, которая состоит из трех точек, которые не
точки А, В, С – вершины,
отрезки АВ, ВС, АС – стороны
∟А, ∟В, ∟С – углы треугольника
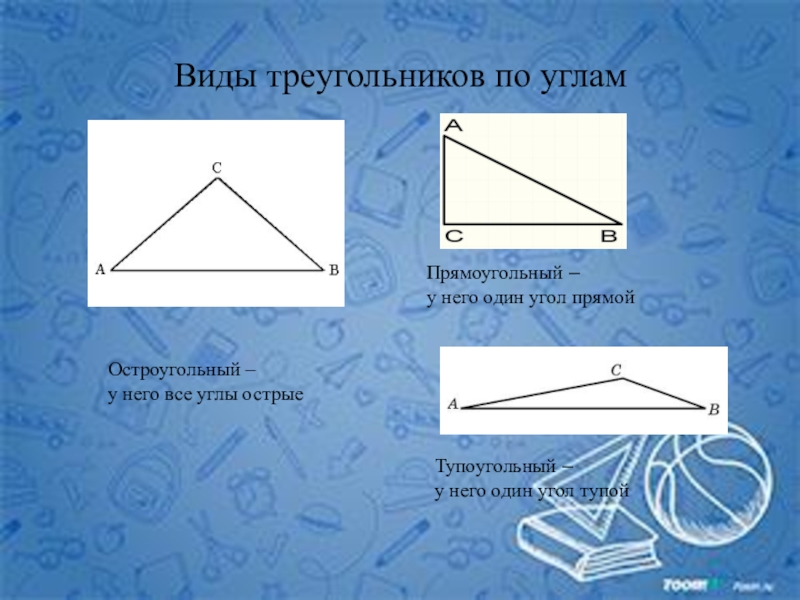
Слайд 7Виды треугольников по углам
Остроугольный –
у него все углы острые
Прямоугольный –
у него один угол прямой
Тупоугольный –
у него один угол тупой
Слайд 8Историческая справка
Треугольник – самая простая замкнутая прямолинейная фигура, одна из первых,
Изображения треугольников и задачи на треугольники встречаются во многих папирусах Древней Греции и Древнего Египта. Древнегреческий ученый Герон (I век) впервые применил знак ∆ вместо слова треугольник.
Слайд 9Практическое применение
треугольников
Равнобедренные треугольники часто встречаются в практике. Например,
Слайд 10Геометрическая фигура «Флексагон» (от англ. to flex, что означает «складываться, гнуться»).
Слайд 11
Египетский треугольник. Землемеры Древнего Египта для построения прямого угла пользовались следующим
Слайд 12
Египетские пирамиды – это одни из грандиозных сооружений, созданных когда-либо руками человека. Самая известная из египетских пирамид – пирамида Хеопса в Гизе. Из-за своих огромных размеров ее иногда еще называют Большой пирамидой. Ее высота составляет 146,6 м, Площадь основания составляет 230*230 м2. Строительство пирамиды Хеопса продолжалось 30 лет. Она состояла из 128 слоев камня и представляла собой ступенчатую гору. Затем ступени были заложены камнями так, что ее поверхность стала хотя и не вполне гладкой, но уже без выступов. В завершении работ четыре треугольные грани пирамиды были облицованы плитами из ослепительно белого известняка и отполированы до зеркального блеска. Края плит были пригнаны настолько точно, что между ними нельзя было вставить даже лезвие острого ножа. По свидетельству очевидцев, на солнце и при лунном свете гробница Хеопса загадочно сверкала, как огромный светящийся изнутри кристалл. Египетская пирамида Хеопса в Гизе – древнейшее, и вместе с тем, единственное сохранившееся до наших дней чудо света.
Слайд 13Тайны пирамиды Хеопса
Пирамиды «умеют» очень многое. Растворимый кофе, например, постояв под
Слайд 14Где же можно встретить треугольники, кроме математики?
Начиная игру в бильярд, необходимо
Слайд 15Правило «золотого треугольника»
Правило «золотого треугольника» основано на психологии покупателя – найдя
Слайд 16Бермудский треугольник
Бермудский треугольник иногда еще называют дьявольским треугольником. Это район в
Слайд 17
Из третьего признака равенства треугольников следует, что треугольник – жесткая фигура.
Представим себе две рейки, у которых два конца скреплены гвоздем. Такая конструкция не является жесткой: сдвигая или раздвигая свободные концы реек, мы можем менять угол между ними. Теперь возьмем еще одну рейку и скрепим ее концы со свободными концами первых двух реек. Полученная конструкция – треугольник – уже будет жесткой. В ней нельзя сдвинуть или раздвинуть никакие две стороны, т.е. нельзя изменить ни один угол. Действительно, если бы это удалось, то мы получили бы новый треугольник, не равный исходному. Но это невозможно, т.к. новый треугольник должен быть равен исходному по третьему признаку равенства треугольников.
Слайд 18
Это свойство – жесткость треугольника – широко используется на практике. Так,
Слайд 20
В глубокой древности вместе с астрономией появилась наука – тригонометрия. Слово
Слайд 21Треугольник Паскаля
Устройство треугольника Паскаля: каждое число равно сумме двух расположенных над
Треугольник Паскаля компьютер перевел на язык цвета.