Решение задач по теме «Треугольники»
Михальчук Н.Л.
учитель математики
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Треугольники(9 класс)
Содержание
- 1. Презентация по геометрии Треугольники(9 класс)
- 2. Треугольник есть первая фигура, которая не может
- 3. Произвольный треугольник
- 4. Произвольный треугольник
- 5. Теорема о свойстве биссектрисы внутреннего угла треугольника
- 6. Длина биссектрисы:
- 7. Свойство медиан в треугольнике:
- 8. Прямоугольный треугольник
- 9. Прямоугольный треугольник
- 10. Равносторонний треугольник 1. Каждая медиана равностороннего треугольника
- 11. Равносторонний треугольник
- 12. Задание № 1.Вычислить площадь треугольника ABC,
- 13. Задание №2. Чему равна площадь
- 14. Слайд 14
- 15. Задание № 4.Найти площадь правильного треугольника, вписанного в окружность радиуса 6 см.
- 16. Задание №5. Найти площадь треугольника со сторонами 9,40 и 41.
- 17. Задание №6. Определите площадь треугольника, если две
- 18. Задание №7. Основание треугольника
- 19. Задание № 8.Стороны треугольника АВС 13,14 и
- 20. Задание №9.Найдите наименьшую высоту треугольника со стонами 17,65 и 80.
- 21. Слайд 21
- 22. Задание № 11.Площадь прямоугольного треугольника 24, а гипотенуза 10. Вычислите радиус окружности, вписанной в данный треугольник.
- 23. ABCТеорема синусов:Стороны треугольника пропорциональны синусам противолежащих угловасb
- 24. Задание №12.Найдите угол В
- 25. MNKНайдите MN
- 26. Слайд 26
- 27. Слайд 27
- 28. ABCТеорема косинусов:Квадрат стороны треугольника равен сумме квадратов
- 29. Задание №16.Найдите длину стороны ВС.АСВ3
- 30. Задание №17.Найдите угол А в треугольнике со сторонами а=14, b=16,с=10.
- 31. Слайд 31
- 32. Задание №19 .В треугольнике АВС известны
- 33. «Знание – самое превосходное из владений. Все
- 34. Пусть ТВОИМ ДЕВИЗОМ, выпускник, станут следующие слова:
Треугольник есть первая фигура, которая не может разложиться в другой вид более простой фигуры (между тем как, наоборот, четырехугольник разлагается на треугольники) и поэтому есть первый фундамент всякой вещи, имеющий границу и фигуру.
Слайд 1Школа КГУ НИСЦ РО «Восток» для одарённых детей управления образования ВКО г.
Усть-Каменогорск
Слайд 2Треугольник есть первая фигура, которая не может разложиться в другой вид
более простой фигуры (между тем как, наоборот, четырехугольник разлагается на треугольники) и поэтому есть первый фундамент всякой вещи, имеющий границу и фигуру.
Бруно Д.
Бруно Д.
Слайд 5Теорема о свойстве биссектрисы внутреннего угла треугольника
Биссектриса внутреннего угла треугольника
делит противоположную сторону на части , пропорциональные прилежащим сторонам:
Слайд 10Равносторонний треугольник
1. Каждая медиана равностороннего треугольника совпадает с биссектрисой и
высотой ,проведенными из той же вершины.
2.Центры вписанной и описанной окружности равностороннего треугольника совпадают.
2.Центры вписанной и описанной окружности равностороннего треугольника совпадают.
Слайд 13 Задание №2. Чему равна площадь равнобедренного треугольника, если его основание 30
см, а боковая сторона 25 см?
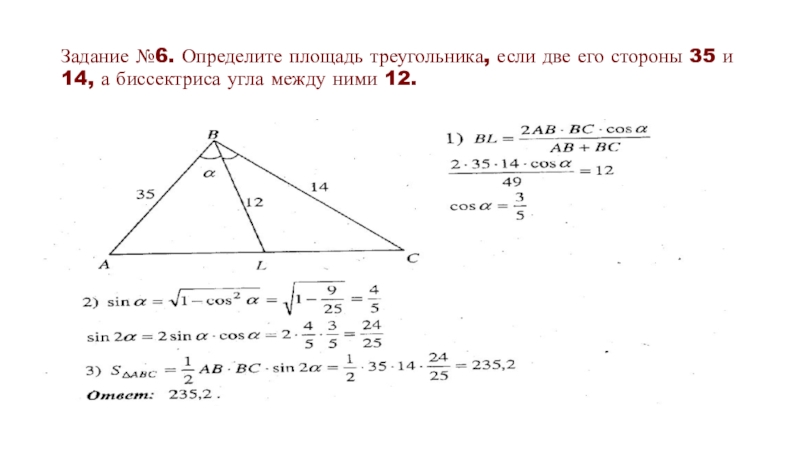
Слайд 17Задание №6. Определите площадь треугольника, если две его стороны 35 и
14, а биссектриса угла между ними 12.
Слайд 18 Задание №7. Основание треугольника АС равно 20,
длины медиан , проведенных к боковым равны 18 и 24 . Найдите площадь треугольника.
Слайд 19Задание № 8.Стороны треугольника АВС 13,14 и 15 .Точка О- точка
пересечения медиан. Найдите площадь треугольника АОВ.
Слайд 22Задание № 11.Площадь прямоугольного треугольника 24, а гипотенуза 10. Вычислите радиус
окружности, вписанной в данный треугольник.
Слайд 28A
B
C
Теорема косинусов:
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус
удвоенное произведение этих сторон на косинус угла между ними
а
с
b
Слайд 32Задание №19 .В треугольнике АВС известны стороны:АВ=3,ВС=5,СА=6.На стороне АВ взята
точка М так что,ВМ=2АМ,а на стороне ВС взята точка К так, что 3ВК=2КС.
Найдите длину отрезка МК.
Слайд 33
«Знание – самое превосходное из владений. Все стремятся к нему, само
же оно не приходит»
Ал - Бируни
Ал - Бируни
Слайд 34Пусть ТВОИМ ДЕВИЗОМ, выпускник, станут следующие слова:
Видеть цель!
Верить в себя!
Добиваться своего!
Не
забывать радоваться!