- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Теорема о трех перпендикулярах
Содержание
- 1. Презентация по геометрии Теорема о трех перпендикулярах
- 2. Геометрия 10Теорема о трех перпендикулярах
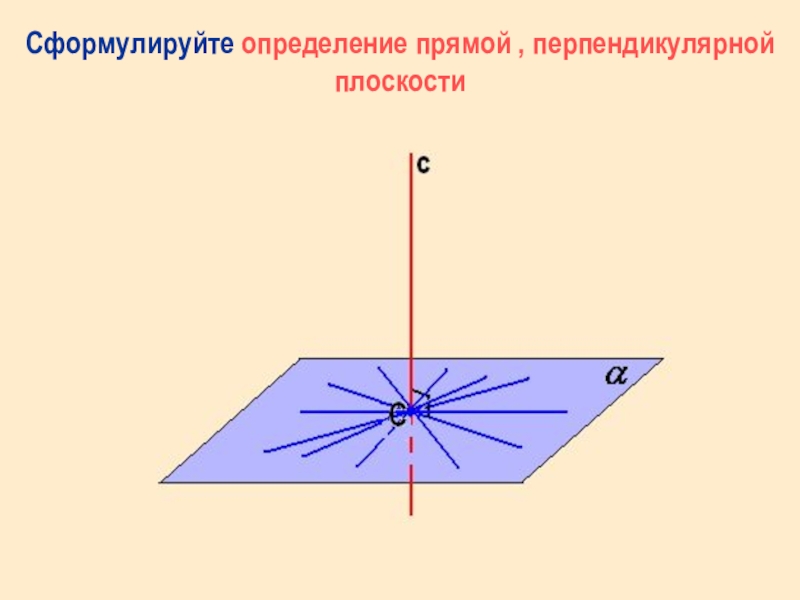
- 3. Сформулируйте определение прямой , перпендикулярной плоскости
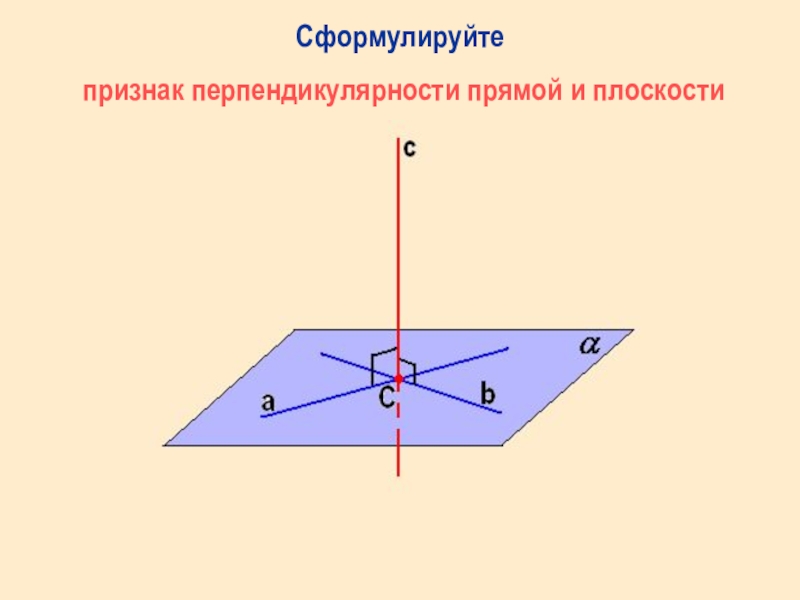
- 4. Сформулируйте признак перпендикулярности прямой и плоскости
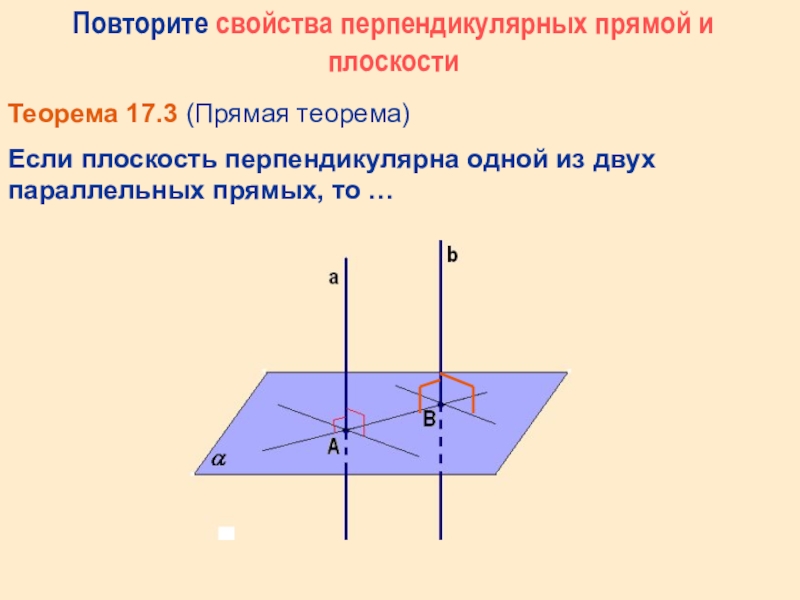
- 5. Повторите свойства перпендикулярных прямой и плоскостиТеорема 17.3
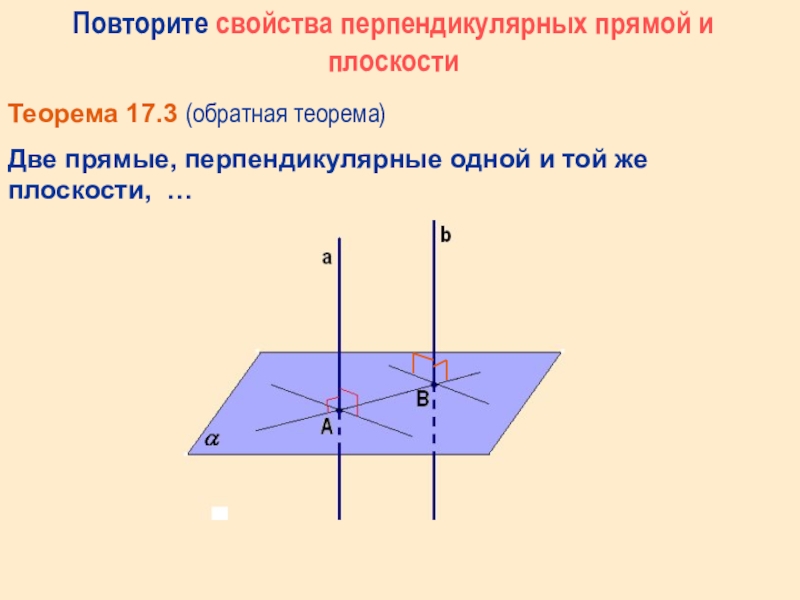
- 6. Повторите свойства перпендикулярных прямой и плоскостиТеорема 17.3
- 7. Если прямая, проведенная на плоскости через основание
- 8. Если прямая на плоскости, перпендикулярна наклонной, то
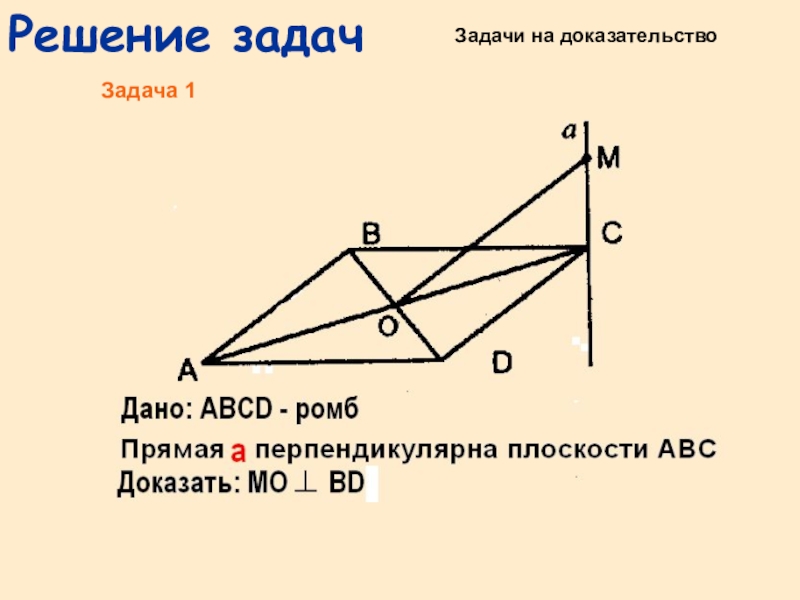
- 9. Решение задачЗадача 1Задачи на доказательство
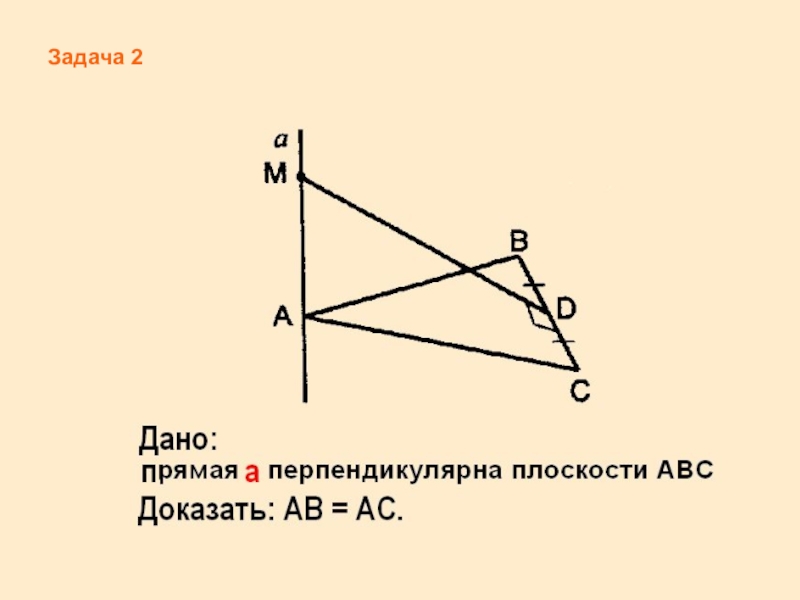
- 10. Задача 2
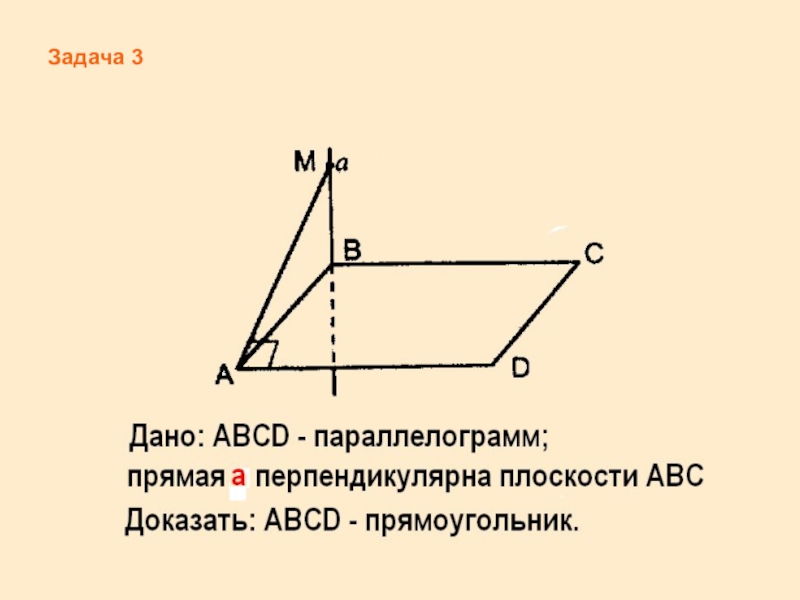
- 11. Задача 3
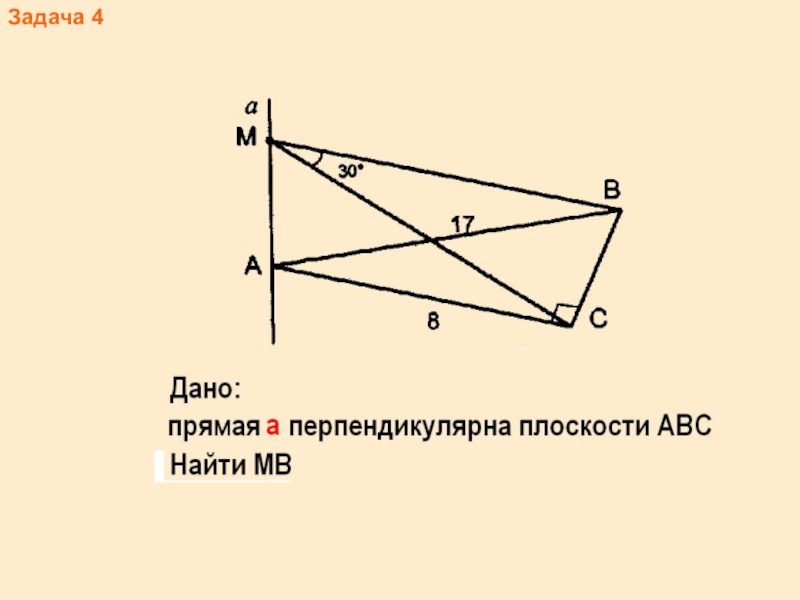
- 12. Задача 4
- 13. Задача 5
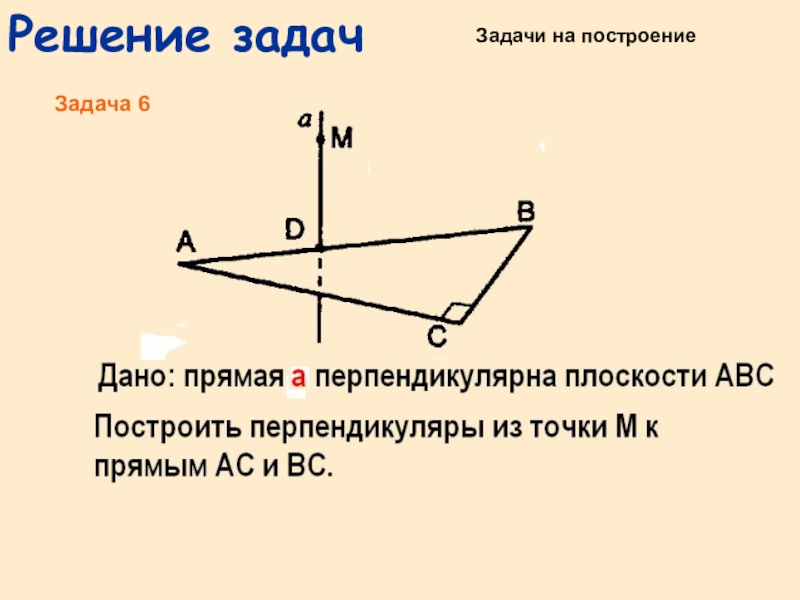
- 14. Решение задачЗадачи на построениеЗадача 6
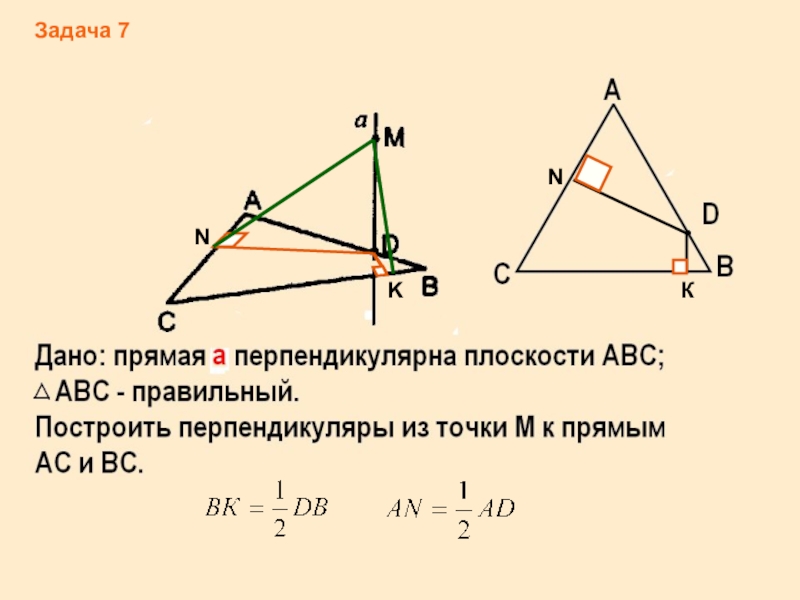
- 15. Задача 7
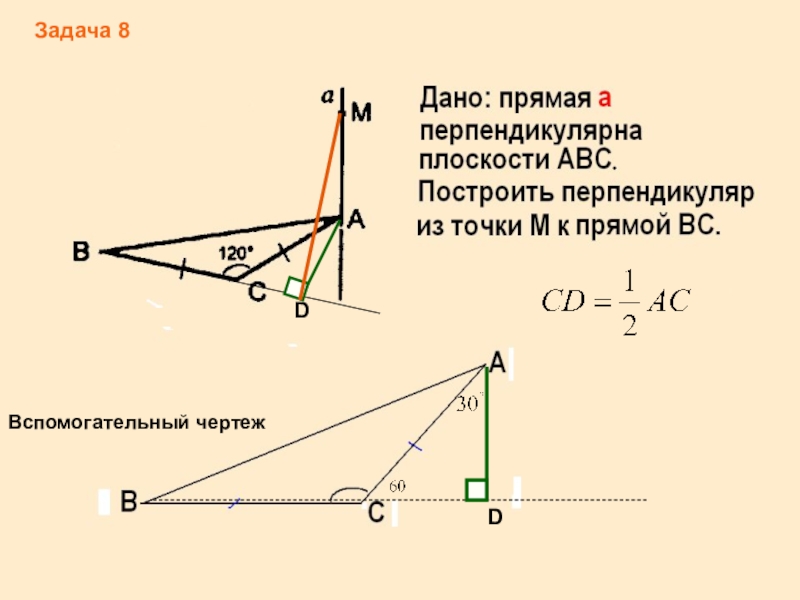
- 16. Вспомогательный чертежЗадача 8
- 17. Тесты (I уровень)Задача 1 Через конец А
- 18. Тесты (I уровень)Задача 2. Отрезок длиной 10
- 19. Тесты (I уровень)Задача 3. Отрезок МН пересекает
- 20. Тесты (I уровень)Задача 4. Через концы отрезка
- 21. Тесты (I уровень)Задача 5. Даны прямоугольник АВСД
Слайд 5Повторите свойства перпендикулярных прямой и плоскости
Теорема 17.3 (Прямая теорема)
Если плоскость перпендикулярна
Слайд 6Повторите свойства перпендикулярных прямой и плоскости
Теорема 17.3 (обратная теорема)
Две прямые, перпендикулярные
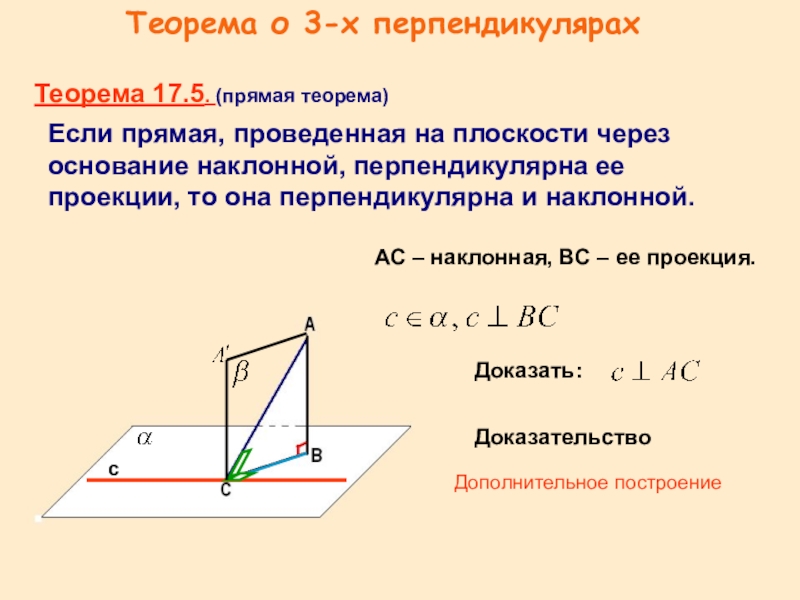
Слайд 7Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции,
АС – наклонная, ВС – ее проекция.
Теорема 17.5. (прямая теорема)
Доказать:
Доказательство
Дополнительное построение
Теорема о 3-х перпендикулярах
Слайд 8Если прямая на плоскости, перпендикулярна наклонной, то она перпендикулярна и проекции
АС – наклонная, ВС – ее проекция.
Теорема 17.5. (обратная теорема)
Доказать:
Доказательство
Дополнительное построение
Слайд 17Тесты (I уровень)
Задача 1 Через конец А отрезка АВ проходит плоскость.
А) 8
Б) 12
В) 10
Г) 4
Выберите правильный ответ
Помощь
По тереме Фалеса ДК – средняя линия треугольника АВС.
Слайд 18Тесты (I уровень)
Задача 2. Отрезок длиной 10 своими концами упирается в
А)6 и 6
Б)6 и 5
В)8 и 8
Г)8 и 5
Помощь
8
Слайд 19Тесты (I уровень)
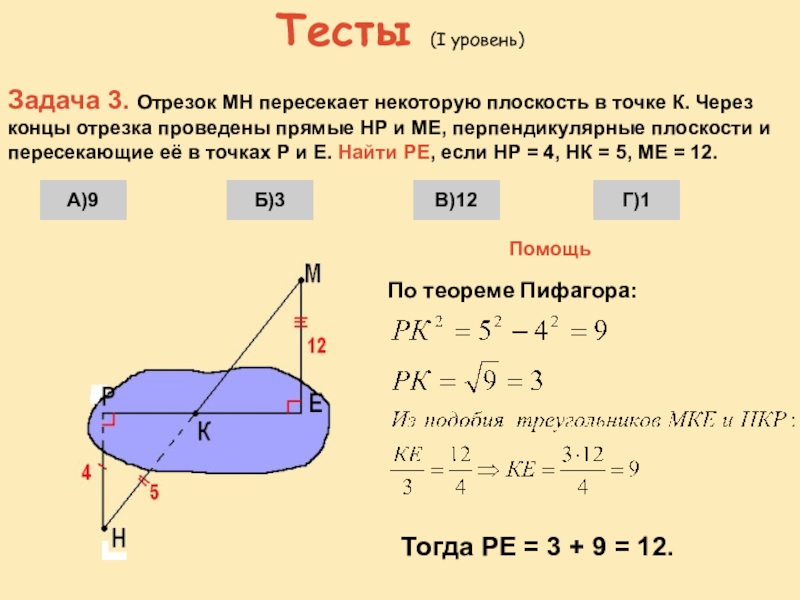
Задача 3. Отрезок МН пересекает некоторую плоскость в точке
А)9
Б)3
Г)1
В)12
Помощь
По теореме Пифагора:
Тогда РЕ = 3 + 9 = 12.
Слайд 20Тесты (I уровень)
Задача 4. Через концы отрезка МН проведены прямые, перпендикулярные
Б)29
В)6
Г)41
Помощь
MN = 5; HN = 6 – 4 = 2.
2
По теореме Пифагора:
Слайд 21Тесты (I уровень)
Задача 5. Даны прямоугольник АВСД и точка Е вне
Г)144
Помощь
В)12
Б)169
А)13
По теореме Пифагора: